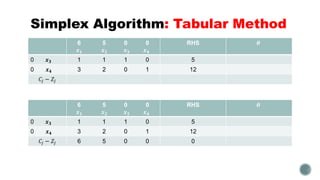
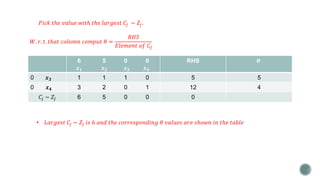
The document summarizes the simplex algorithm for solving linear programs. It discusses how the simplex algorithm works by generating a sequence of basic feasible solutions until it finds an optimal solution. It provides the standard form for a linear program and describes how the simplex algorithm sets up a tableau to solve the problem using an iterative method. Finally, it provides an example linear program and begins setting up the tableau to solve it using the simplex algorithm's tabular method.

1. Combinatorial Optimization
CS-724
Lec-7:
Date: 03-03-2021
Dr. Parikshit Saikia
Assistant Professor
Department of Computer Science and Engineering
NIT Hamirpur (HP)
India

2. Simplex Algorithm
 [1947]. George B. Dantzig developed a technique to solve linear
programs----known as Simplex Algorithm
 The simplex method is an iterative method that generates a sequence
of basic feasible solutions (corresponding to different bases) and
eventually stops when it has found an optimal basic feasible solution.

3.  The given LP is in the Standard form.
𝑚𝑖𝑛𝑖𝑚𝑖𝑧𝑒 (𝑜𝑟 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒) 𝑐′𝑥
𝐴𝑥 = 𝑏
𝑥 ≥ 0
 𝑏 ≥ 0
 There exists a collection 𝑩 of m variables called a basis such that
 the submatrix 𝑨𝑩 of 𝑨 consisting of the columns of 𝑨 corresponding to the variables in
𝑩 is the 𝑚 × 𝑚 identity matrix and
 the cost coefficients corresponding to the variables in 𝑩 are all equal to 𝟎.

4. Simplex Algorithm: Tabular Method
Solve the following LP using Tabular Method
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 6𝑥1 + 5𝑥2
𝑆𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝑥1 + 𝑥2 ≤ 5
3𝑥1 + 2𝑥2 ≤ 12
𝑥1, 𝑥2 ≥ 0

5. Simplex Algorithm: Tabular Method
The standard form of the given LP is
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 𝑍 = 6𝑥1 + 5𝑥2 + 0. 𝑥3 + 0. 𝑥4
𝑆𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝑥1 + 𝑥2 + 𝑥3 = 5
3𝑥1 + 2𝑥2 + 𝑥4 = 12
𝑥1, 𝑥2, 𝑥3, 𝑥4 ≥ 0
𝐻𝑒𝑟𝑒 𝑥3 𝑎𝑛𝑑 𝑥4 𝑎𝑟𝑒 𝑠𝑙𝑎𝑐𝑘 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠.

6. Simplex Algorithm: Tabular Method
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 𝑍 = 6𝑥1 + 5𝑥2 + 0. 𝑥3 + 0. 𝑥4
𝑆𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝑥1 + 𝑥2 + 𝑥3 = 5
3𝑥1 + 2𝑥2 + 𝑥4 = 12
𝑥1, 𝑥2, 𝑥3, 𝑥4 ≥ 0
6 5 0 0
𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒
RHS 𝜽
0 𝒙𝟑 1 1 1 0 5
0 𝒙𝟒 3 2 0 1 12
𝐶𝑗 − 𝑍𝑗
𝑪𝒋 − 𝒁𝑱 𝒊𝒔 𝒖𝒔𝒆𝒅 𝒕𝒐 𝒑𝒊𝒄𝒌 𝒕𝒉𝒆 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆 𝒘𝒉𝒊𝒄𝒉 𝒘𝒊𝒍𝒍 𝒃𝒆 𝒕𝒉𝒆 𝒃𝒂𝒔𝒊𝒄 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆 𝒊𝒏 𝒕𝒉𝒆 𝒏𝒆𝒙𝒕 𝒊𝒕𝒆𝒓𝒂𝒕𝒊𝒐𝒏
Algorithm terminates when 𝑪𝒋 − 𝒁𝒋 ≤ 𝟎. In this state the current basic feasible solution is optimal.

7. Simplex Algorithm: Tabular Method
6 5 0 0
𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒
RHS 𝜽
0 𝒙𝟑 1 1 1 0 5
0 𝒙𝟒 3 2 0 1 12
𝐶𝑗 − 𝑍𝑗
6 5 0 0
𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒
RHS 𝜽
0 𝒙𝟑 1 1 1 0 5
0 𝒙𝟒 3 2 0 1 12
𝐶𝑗 − 𝑍𝑗 6 5 0 0 0

8. 6 5 0 0
𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒
RHS 𝜽
0 𝒙𝟑 1 1 1 0 5 5
0 𝒙𝟒 3 2 0 1 12 4
𝐶𝑗 − 𝑍𝑗 6 5 0 0 0
• 𝐿𝑎𝑟𝑔𝑒𝑠𝑡 𝐶𝑗 − 𝑍𝑗 𝑖𝑠 6 𝑎𝑛𝑑 𝑡ℎ𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝜃 𝑣𝑎𝑙𝑢𝑒𝑠 𝑎𝑟𝑒 𝑠ℎ𝑜𝑤𝑛 𝑖𝑛 𝑡ℎ𝑒 𝑡𝑎𝑏𝑙𝑒
𝑃𝑖𝑐𝑘 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒 𝑤𝑖𝑡ℎ 𝑡ℎ𝑒 𝑙𝑎𝑟𝑔𝑒𝑠𝑡 𝐶𝑗 − 𝑍𝑗.
𝑊. 𝑟. 𝑡. 𝑡ℎ𝑎𝑡 𝑐𝑜𝑙𝑢𝑚𝑛 𝑐𝑜𝑚𝑝𝑢𝑡 𝜃 =
𝑅𝐻𝑆
𝐸𝑙𝑒𝑚𝑒𝑛𝑡 𝑜𝑓 𝐶𝐽

9. • Pick the row with smallest 𝜃 𝑣𝑎𝑙𝑢𝑒 𝑎𝑠 𝑎 𝑝𝑖𝑣𝑜𝑡𝑒 𝑟𝑜𝑤
𝑎𝑛𝑑
• 𝑡ℎ𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑒𝑙𝑒𝑚𝑒𝑛𝑡 𝑖𝑛 𝐶𝑗 𝑤ℎ𝑖𝑐ℎ 𝑝𝑟𝑜𝑑𝑢𝑐𝑒𝑠 𝑡ℎ𝑒
smallest 𝜃 value is considered as the pivot element

12. Solve the following LP using Simplex Algorithm
𝑀𝑎𝑥 𝑍 = 2𝑥1 − 𝑥2 + 2𝑥3
𝑠. 𝑡. 2𝑥1 + 𝑥2 ≤ 10
𝑥1 + 2𝑥2 − 2𝑥3 ≤ 20
𝑥1 + 2𝑥3 ≤ 5
𝑥1, 𝑥2, 𝑥_3 ≥ 0