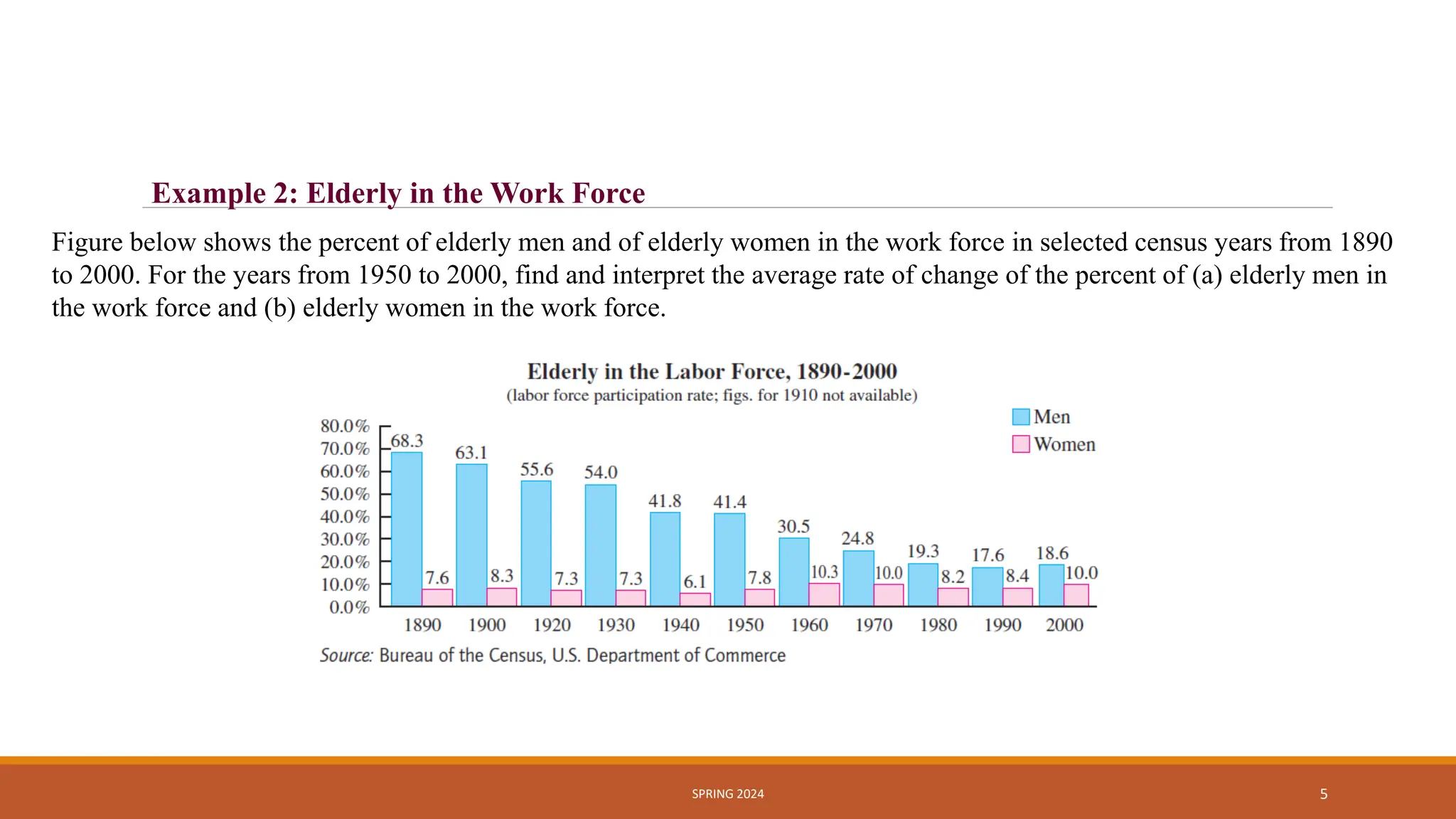
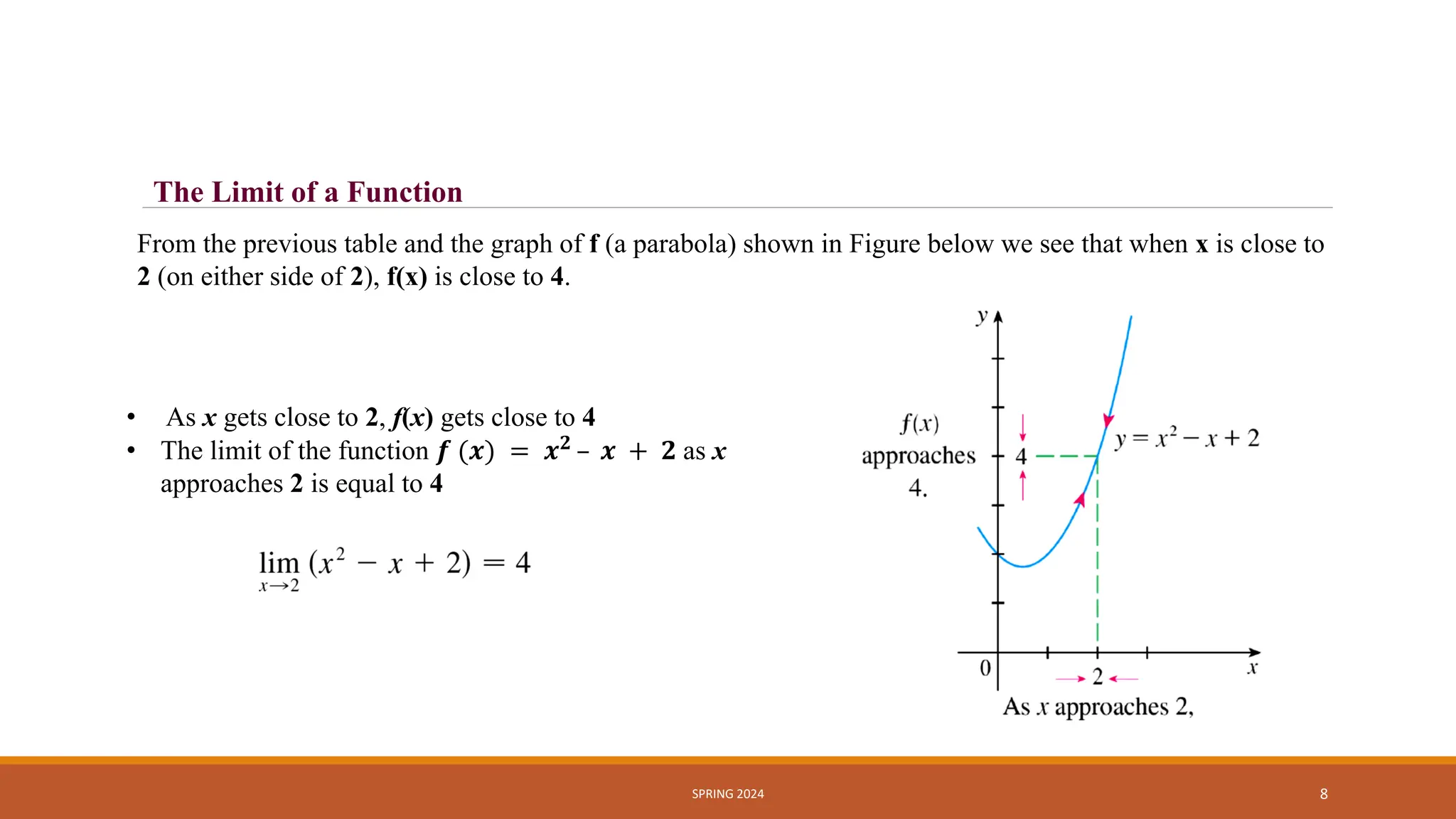
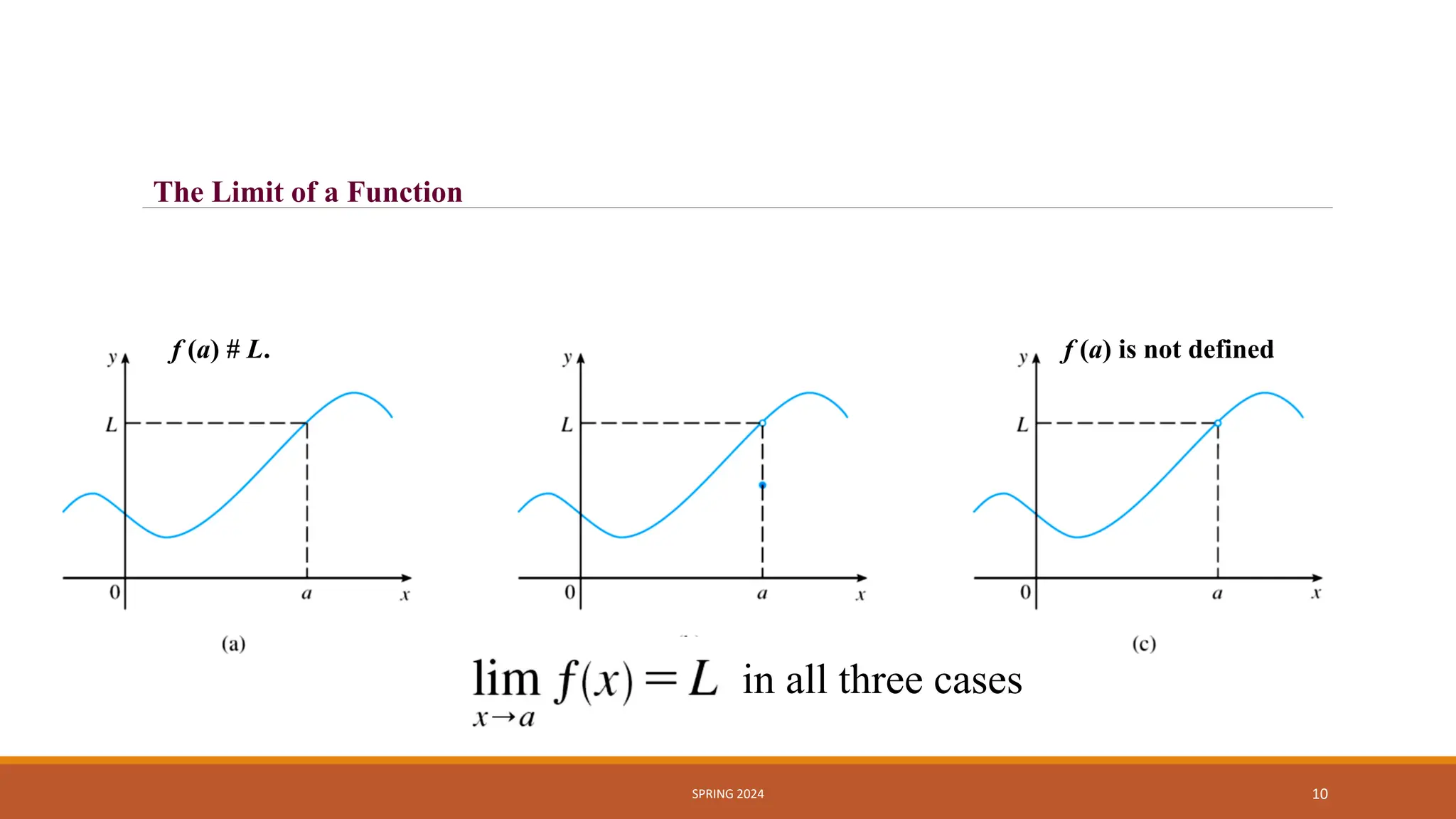
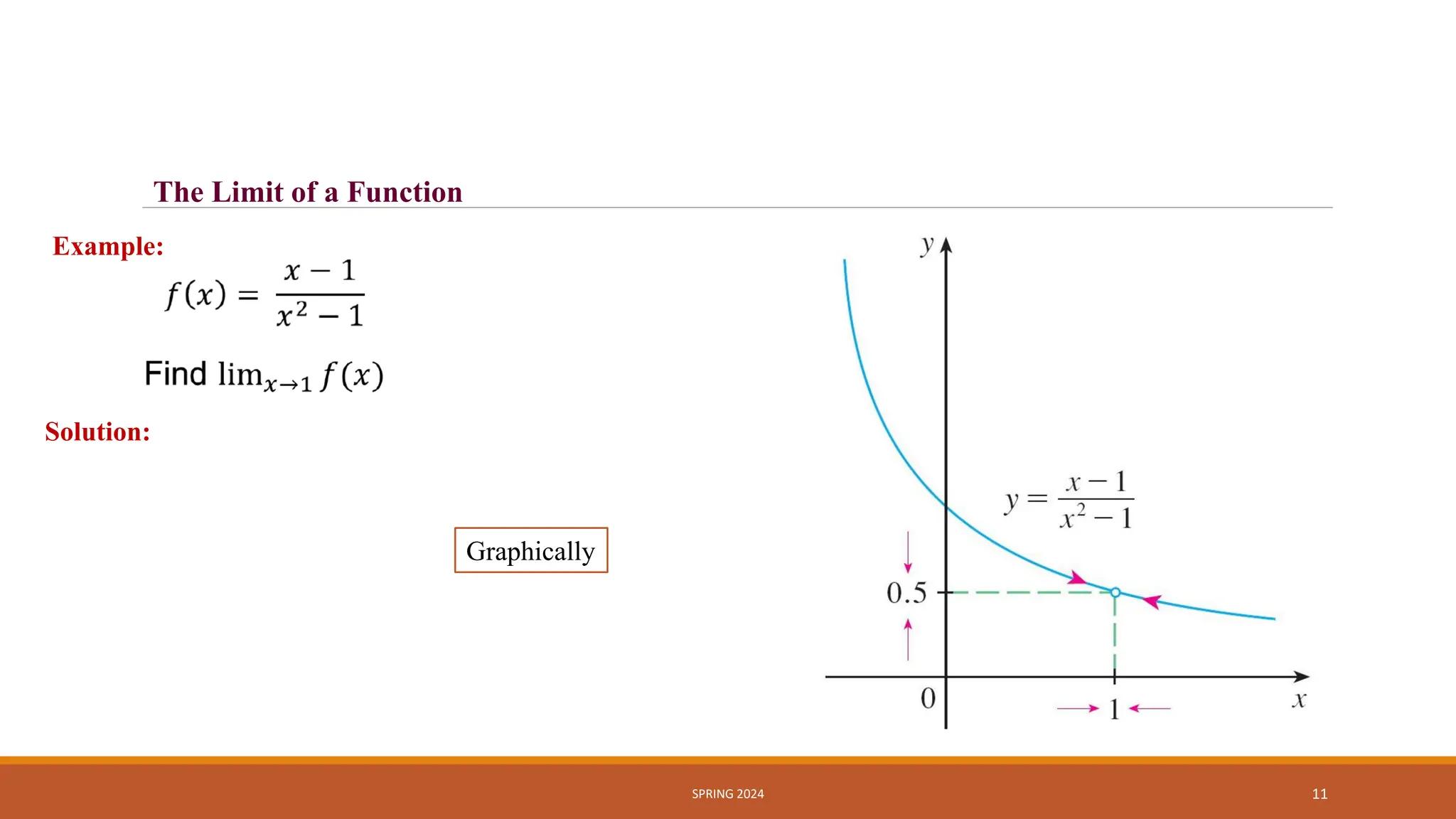
This document discusses average and instantaneous rates of change and limits of functions. 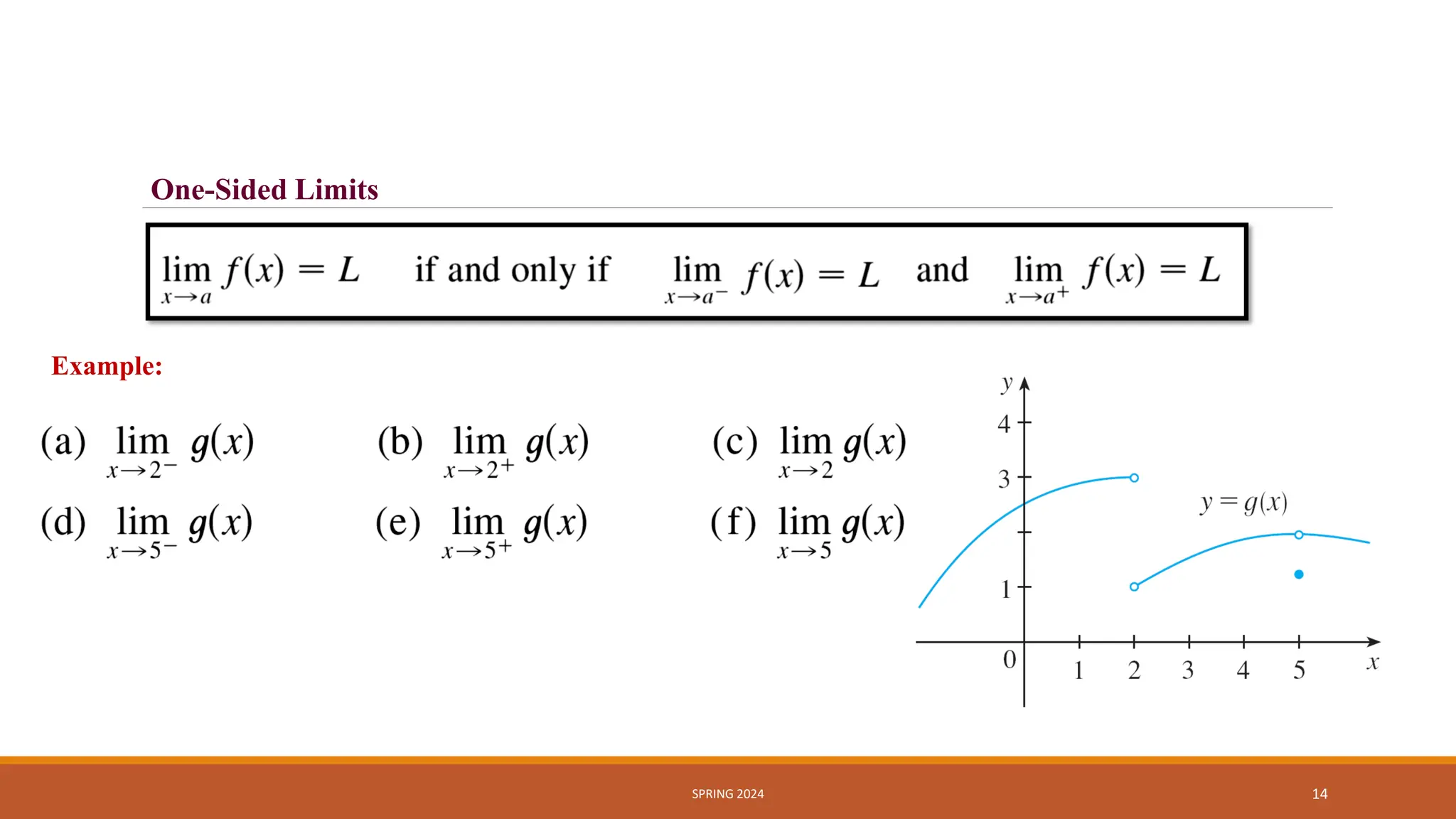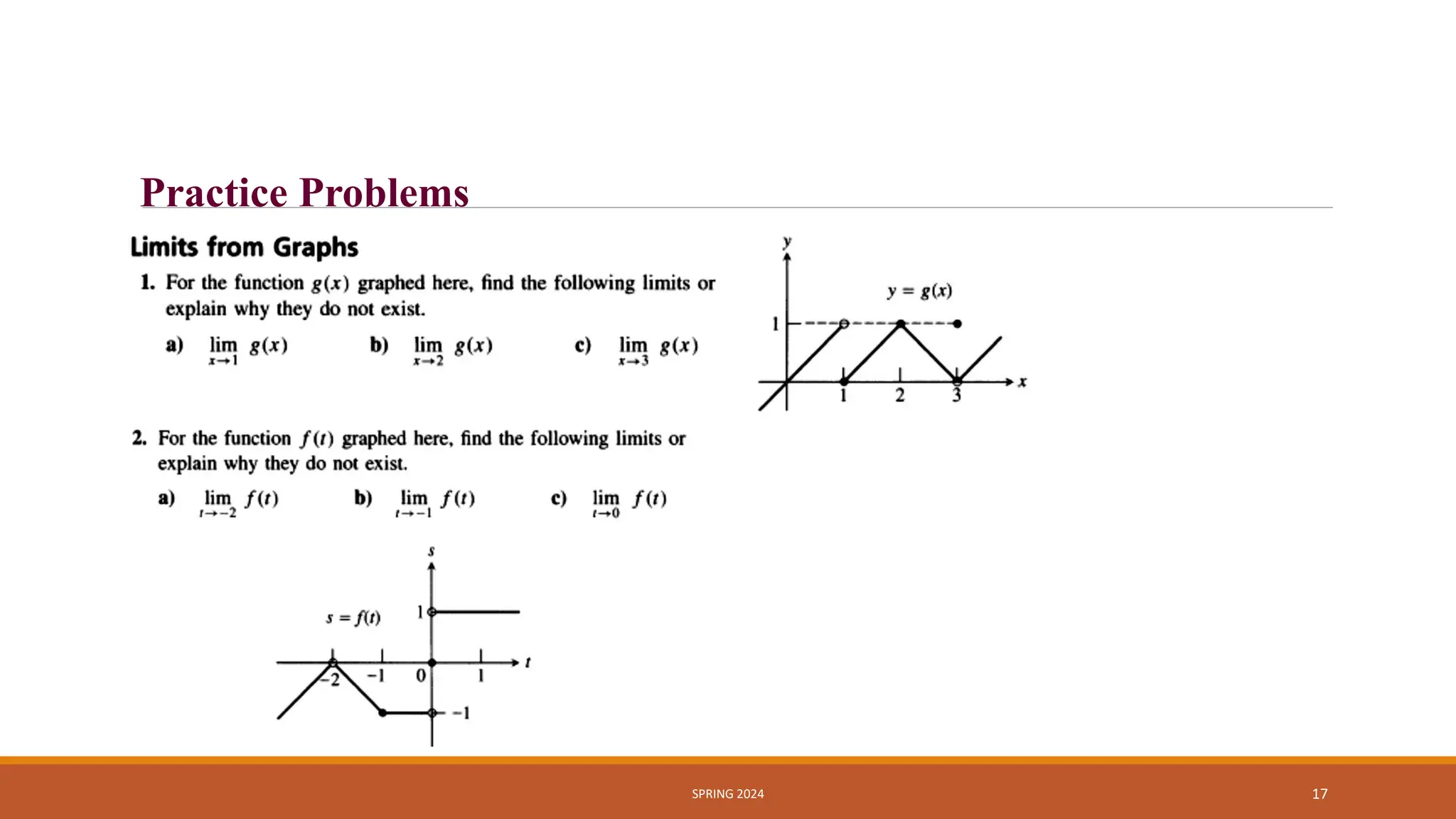It provides examples and definitions of: - Average rate of change, which represents total change over total change - Instantaneous rate of change, which measures change over infinitesimally small changes - Limits of functions as the input approaches a value, where the limit is the value the function approaches - One-sided limits, where the left and right limits may differ or agree It also distinguishes between average speed, which is distance over time, and average velocity, which is displacement over time.

1. SPRING 2024 1
LIMITS
Calculus and Analytical Geometry

2. SPRING 2024 2
Average and Instantaneous Change
What is the rate of change?
Rate of change is the change in one variable in relation to the change in another variable.
• The average rate of change represents the total change in one variable in relation to the total change of
another variable.
• Instantaneous rate of change, measures the rate of change of one variable in relation to infinitesimally
small change in the other variable.

3. SPRING 2024 3
Average and Instantaneous Change

4. SPRING 2024 4
Example 1: Total Cost
Suppose a company’s total cost in dollars to produce x units of its product is given by
Find the average rate of change of total cost for (a) the first 100 units produced (from to ) and (b) the second 100 units
produced.

5. SPRING 2024 5
Figure below shows the percent of elderly men and of elderly women in the work force in selected census years from 1890
to 2000. For the years from 1950 to 2000, find and interpret the average rate of change of the percent of (a) elderly men in
the work force and (b) elderly women in the work force.
Example 2: Elderly in the Work Force

6. SPRING 2024 6
Example 2: Elderly in the Work Force

7. SPRING 2024 7
The Limit of a Function
Let’s investigate the behavior of the function f defined by
for values of x near 2.
The following table gives values of f(x) for values of x close to 2 but not equal to 2.
𝒇 (𝒙) = 𝒙𝟐 – 𝒙 + 𝟐

8. SPRING 2024 8
From the previous table and the graph of f (a parabola) shown in Figure below we see that when x is close to
2 (on either side of 2), f(x) is close to 4.
• As x gets close to 2, f(x) gets close to 4
• The limit of the function 𝒇 (𝒙) = 𝒙𝟐
– 𝒙 + 𝟐 as x
approaches 2 is equal to 4
The Limit of a Function

9. SPRING 2024 9
The Limit of a Function
• An alternative notation is f (x)  L as x  a which is usually read “f (x) approaches L as x approaches a.”
• Notice the phrase “but x # a” in the definition of limit. This means that in finding the limit of f (x) as x approaches a, it
does not matter what is happening at x = a.
• In fact, f (x) need not even be defined when x = a. The only thing that matters is how f is defined near a.

10. SPRING 2024 10
in all three cases
f (a) is not defined
f (a) # L.
The Limit of a Function

11. SPRING 2024 11
Example:
Solution:
The Limit of a Function
Graphically

12. SPRING 2024 12
On the basis of the values in the tables, we can say
Numerically
The Limit of a Function

13. SPRING 2024 13
One-Sided Limits
The Heaviside function H is defined by
• H(t) approaches 0 as t approaches 0 from the left and H(t) approaches 1 as t approaches 0 from the right.
• We indicate this situation symbolically by writing

14. SPRING 2024 14
One-Sided Limits
Example:

15. SPRING 2024 15
Solution:
(c) Since the left and right limits are different, we conclude from that limx2 g(x) does not exist
(f) This time the left and right limits are the same, so
One-Sided Limits

16. SPRING 2024 16
Practice Problems

17. SPRING 2024 17
Practice Problems

18. SPRING 2024 18
Practice Problems

19. SPRING 2024 19
Practice Problems

20. SPRING 2024 20
Average speed is calculated as the distance traveled over the total time of travel.
In contrast, average velocity is defined as the change in position (or displacement) over the total time of travel
average speed of 40/30 = 1.33 m/s
Displacement is 0 meters. Therefore, average velocity, or displacement over time, would be 0 m/s
Average speed and Average Velocity