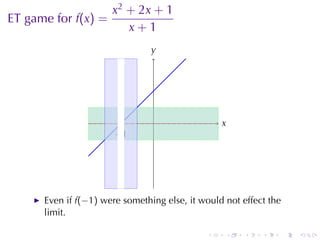
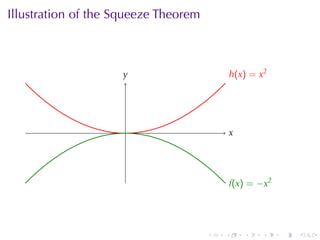
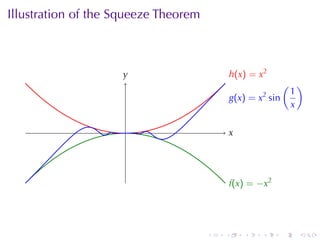
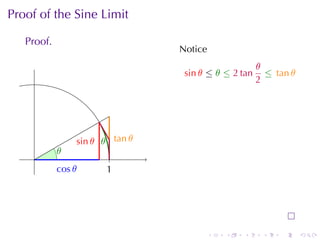
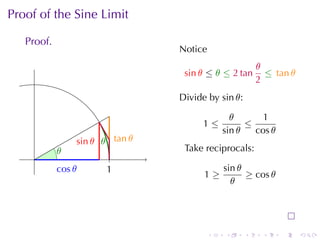
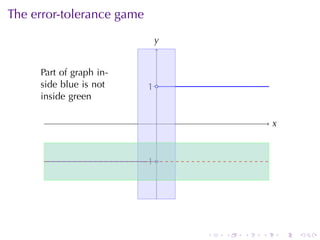
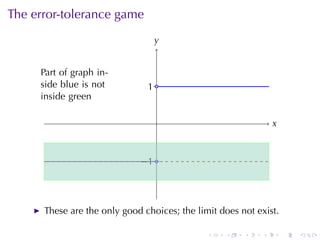
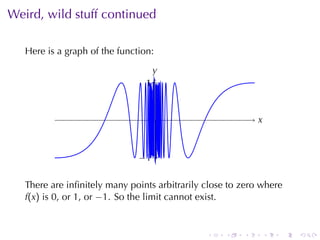
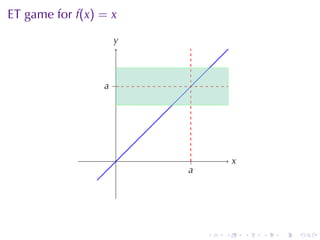
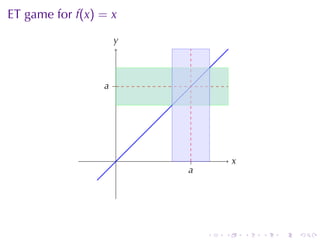
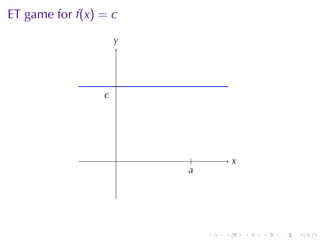
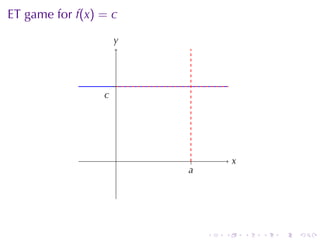
This document outlines the principles of calculating limits in calculus, including definitions and theorems related to limits, one-sided limits, and examples demonstrating their application. It explains the error-tolerance game as a means to determine the existence of a limit and discusses various limit pathologies that may occur. Additionally, the document includes historical notes on mathematician Augustin Louis Cauchy and basic properties of limits and arithmetic operations involving them.

1. Section 1.4
Calculating Limits
V63.0121.034, Calculus I
September 14, 2009
Announcements
First written assignment due Wednesday
First web assignment due Monday, September 21
. . . . . .

2. Outline
Limits and Pathologies
Basic Limits
Limit Laws
The direct substitution property
Limits with Algebra
Two more limit theorems
Two important trigonometric limits
. . . . . .

3. Heuristic Definition of a Limit
Definition
We write
lim f(x) = L
x→a
and say
“the limit of f(x), as x approaches a, equals L”
if we can make the values of f(x) arbitrarily close to L (as close to
L as we like) by taking x to be sufficiently close to a (on either
side of a) but not equal to a.
. . . . . .

4. The error-tolerance game
A game between two players to decide if a limit lim f(x) exists.
x→a
Player 1: Choose L to be the limit.
Player 2: Propose an “error” level around L.
Player 1: Choose a “tolerance” level around a so that
x-points within that tolerance level are taken to y-values
within the error level.
If Player 1 can always win, lim f(x) = L.
x→a
. . . . . .

5. Example
Find lim x2 if it exists.
x→0
. . . . . .

6. Example
Find lim x2 if it exists.
x→0
Solution
I claim the limit is zero.
. . . . . .

7. Example
Find lim x2 if it exists.
x→0
Solution
I claim the limit is zero.
If the error level is 0.01, I need to guarantee that
−0.01 < x2 < 0.01 for all x sufficiently close to zero.
. . . . . .

8. Example
Find lim x2 if it exists.
x→0
Solution
I claim the limit is zero.
If the error level is 0.01, I need to guarantee that
−0.01 < x2 < 0.01 for all x sufficiently close to zero.
If −0.1 < x < 0.1, then 0 ≤ x2 < 0.01, so I win that round.
. . . . . .

9. Example
Find lim x2 if it exists.
x→0
Solution
I claim the limit is zero.
If the error level is 0.01, I need to guarantee that
−0.01 < x2 < 0.01 for all x sufficiently close to zero.
If −0.1 < x < 0.1, then 0 ≤ x2 < 0.01, so I win that round.
What should the tolerance be if the error is 0.0001?
. . . . . .

10. Example
Find lim x2 if it exists.
x→0
Solution
I claim the limit is zero.
If the error level is 0.01, I need to guarantee that
−0.01 < x2 < 0.01 for all x sufficiently close to zero.
If −0.1 < x < 0.1, then 0 ≤ x2 < 0.01, so I win that round.
What should the tolerance be if the error is 0.0001?
By setting tolerance equal to the square root of the error, we can
guarantee to be within any error.
. . . . . .

11. Example
|x|
Find lim if it exists.
x→0 x
. . . . . .

12. Example
|x|
Find lim if it exists.
x→0 x
Solution
The function can also be written as
{
|x| 1 if x > 0;
=
x −1 if x < 0
What would be the limit?
. . . . . .

13. The error-tolerance game
y
.
. .
1
. x
.
. 1.
−
. . . . . .

14. The error-tolerance game
y
.
. .
1
. x
.
. 1.
−
. . . . . .

15. The error-tolerance game
y
.
. .
1
. x
.
. 1.
−
. . . . . .

16. The error-tolerance game
y
.
. .
1
. x
.
. 1.
−
. . . . . .

17. The error-tolerance game
y
.
. .
1
. x
.
.
Part of graph in-
. 1.
− side blue is not
inside green
. . . . . .

18. The error-tolerance game
y
.
. .
1
. x
.
. 1.
−
. . . . . .

19. The error-tolerance game
y
.
. .
1
. x
.
. 1.
−
. . . . . .

20. The error-tolerance game
y
.
.
Part of graph in-
side blue is not . .
1
inside green
. x
.
. 1.
−
. . . . . .

21. The error-tolerance game
y
.
.
Part of graph in-
side blue is not . .
1
inside green
. x
.
. 1.
−
These are the only good choices; the limit does not exist.
. . . . . .

22. One-sided limits
Definition
We write
lim f(x) = L
x→a+
and say
“the limit of f(x), as x approaches a from the right, equals L”
if we can make the values of f(x) arbitrarily close to L (as close to
L as we like) by taking x to be sufficiently close to a (on either
side of a) and greater than a.
. . . . . .

23. One-sided limits
Definition
We write
lim f(x) = L
x→a−
and say
“the limit of f(x), as x approaches a from the left, equals L”
if we can make the values of f(x) arbitrarily close to L (as close to
L as we like) by taking x to be sufficiently close to a (on either
side of a) and less than a.
. . . . . .

24. Example
|x|
Find lim if it exists.
x→0 x
Solution
The function can also be written as
{
|x| 1 if x > 0;
=
x −1 if x < 0
What would be the limit?
The error-tolerance game fails, but
lim f(x) = 1 lim f(x) = −1
x→0+ x→0−
. . . . . .

25. Example
1
Find lim if it exists.
x→0+ x
. . . . . .

26. The error-tolerance game
y
.
.? .
L
. x
.
0
.
. . . . . .

27. The error-tolerance game
y
.
.? .
L
. x
.
0
.
. . . . . .

28. The error-tolerance game
y
.
.? .
L
. x
.
0
.
. . . . . .

29. The error-tolerance game
y
.
.
The graph escapes the
green, so no good
.? .
L
. x
.
0
.
. . . . . .

30. The error-tolerance game
y
.
.? .
L
. x
.
0
.
. . . . . .

31. The error-tolerance game
y
.
E
. ven worse!
.? .
L
. x
.
0
.
. . . . . .

32. The error-tolerance game
y
.
.
The limit does not exist
because the function is
unbounded near 0
.? .
L
. x
.
0
.
. . . . . .

33. Example
1
Find lim if it exists.
x→0+ x
Solution
The limit does not exist because the function is unbounded near
0. Next week we will understand the statement that
1
lim = +∞
x→0+ x
. . . . . .

34. Weird, wild stuff
Example (π )
Find lim sin if it exists.
x→0 x
. . . . . .

35. Weird, wild stuff
Example (π )
Find lim sin if it exists.
x→0 x
f(x) = 0 when x =
f(x) = 1 when x =
f(x) = −1 when x =
. . . . . .

36. Weird, wild stuff
Example (π )
Find lim sin if it exists.
x→0 x
1
f(x) = 0 when x = for any integer k
k
f(x) = 1 when x =
f(x) = −1 when x =
. . . . . .

37. Weird, wild stuff
Example (π )
Find lim sin if it exists.
x→0 x
1
f(x) = 0 when x = for any integer k
k
1
f(x) = 1 when x = for any integer k
2k + 1/2
f(x) = −1 when x =
. . . . . .

38. Weird, wild stuff
Example (π )
Find lim sin if it exists.
x→0 x
1
f(x) = 0 when x = for any integer k
k
1
f(x) = 1 when x = for any integer k
2k + 1/2
1
f(x) = −1 when x = for any integer k
2k − 1/2
. . . . . .

39. Weird, wild stuff continued
Here is a graph of the function:
y
.
. .
1
. x
.
. 1.
−
There are infinitely many points arbitrarily close to zero where
f(x) is 0, or 1, or −1. So the limit cannot exist.
. . . . . .

40. What could go wrong?
Summary of Limit Pathologies
How could a function fail to have a limit? Some possibilities:
left- and right- hand limits exist but are not equal
The function is unbounded near a (possible infinite limits,
more later)
Oscillation with increasingly high frequency near a
. . . . . .

41. Meet the Mathematician: Augustin Louis Cauchy
French, 1789–1857
Royalist and Catholic
made contributions in
geometry, calculus,
complex analysis,
number theory
created the definition of
limit we use today but
didn’t understand it
. . . . . .

42. Outline
Limits and Pathologies
Basic Limits
Limit Laws
The direct substitution property
Limits with Algebra
Two more limit theorems
Two important trigonometric limits
. . . . . .

43. Really basic limits
Fact
Let c be a constant and a a real number.
(i) lim x = a
x→a
(ii) lim c = c
x→a
. . . . . .

44. Really basic limits
Fact
Let c be a constant and a a real number.
(i) lim x = a
x→a
(ii) lim c = c
x→a
Proof.
The first is tautological, the second is trivial.
. . . . . .

45. ET game for f(x) = x
y
.
. x
.
. . . . . .

46. ET game for f(x) = x
y
.
. x
.
. . . . . .

47. ET game for f(x) = x
y
.
. .
a
. . x
.
a
.
. . . . . .

48. ET game for f(x) = x
y
.
. .
a
. . x
.
a
.
. . . . . .

49. ET game for f(x) = x
y
.
. .
a
. . x
.
a
.
. . . . . .

50. ET game for f(x) = x
y
.
. .
a
. . x
.
a
.
. . . . . .

51. ET game for f(x) = x
y
.
. .
a
. . x
.
a
.
Setting error equal to tolerance works!
. . . . . .

52. ET game for f(x) = c
.
. . . . . .

53. ET game for f(x) = c
y
.
. x
.
. . . . . .

54. ET game for f(x) = c
y
.
. x
.
. . . . . .

55. ET game for f(x) = c
y
.
.
c
.
. . x
.
a
.
. . . . . .

56. ET game for f(x) = c
y
.
.
c
.
. . x
.
a
.
. . . . . .

57. ET game for f(x) = c
y
.
.
c
.
. . x
.
a
.
. . . . . .

58. ET game for f(x) = c
y
.
.
c
.
. . x
.
a
.
any tolerance works!
. . . . . .

59. Really basic limits
Fact
Let c be a constant and a a real number.
(i) lim x = a
x→a
(ii) lim c = c
x→a
Proof.
The first is tautological, the second is trivial.
. . . . . .

60. Outline
Limits and Pathologies
Basic Limits
Limit Laws
The direct substitution property
Limits with Algebra
Two more limit theorems
Two important trigonometric limits
. . . . . .

61. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x)
x→a x→a x→a
. . . . . .

62. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
. . . . . .

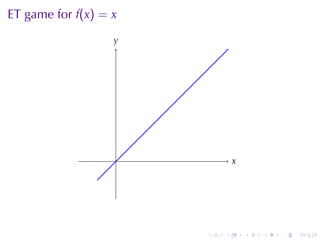
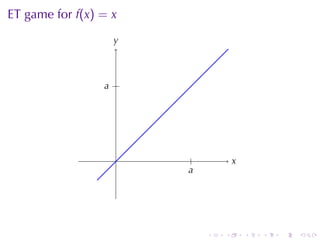
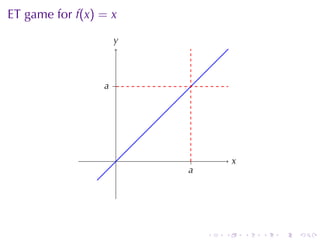
63. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
2. lim [f(x) − g(x)] = lim f(x) − lim g(x)
x→a x→a x→a
. . . . . .

64. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
2. lim [f(x) − g(x)] = lim f(x) − lim g(x)
x→a x→a x→a
3. lim [cf(x)] = c lim f(x)
x→a x→a
. . . . . .

65. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
2. lim [f(x) − g(x)] = lim f(x) − lim g(x)
x→a x→a x→a
3. lim [cf(x)] = c lim f(x) (error scales)
x→a x→a
. . . . . .

66. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
2. lim [f(x) − g(x)] = lim f(x) − lim g(x) (combination of adding
x→a x→a x→a
and scaling)
3. lim [cf(x)] = c lim f(x) (error scales)
x→a x→a
. . . . . .

67. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
2. lim [f(x) − g(x)] = lim f(x) − lim g(x) (combination of adding
x→a x→a x→a
and scaling)
3. lim [cf(x)] = c lim f(x) (error scales)
x→a x→a
4. lim [f(x)g(x)] = lim f(x) · lim g(x)
x→a x→a x→a
. . . . . .

68. Limits and arithmetic
Fact
Suppose lim f(x) and lim g(x) exist and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = lim f(x) + lim g(x) (errors add)
x→a x→a x→a
2. lim [f(x) − g(x)] = lim f(x) − lim g(x) (combination of adding
x→a x→a x→a
and scaling)
3. lim [cf(x)] = c lim f(x) (error scales)
x→a x→a
4. lim [f(x)g(x)] = lim f(x) · lim g(x) (more complicated, but
x→a x→a x→a
doable)
. . . . . .

69. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
. . . . . .

70. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
[ ]n
6. lim [f(x)]n = lim f(x)
x→a x→a
. . . . . .

71. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
[ ]n
6. lim [f(x)]n = lim f(x) (follows from 4 repeatedly)
x→a x→a
. . . . . .

72. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
[ ]n
6. lim [f(x)]n = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a
x→a
. . . . . .

73. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
[ ]n
6. lim [f(x)]n = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a
x→a
√ √
8. lim n x = n a
x→a
. . . . . .

74. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
[ ]n
6. lim [f(x)]n = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a (follows from 6)
x→a
√ √
8. lim n x = n a
x→a
. . . . . .

75. Limits and arithmetic II
Fact (Continued)
f (x ) lim f(x)
5. lim = x→a , if lim g(x) ̸= 0.
x→a g(x) lim g(x) x→a
x→a
[ ]n
6. lim [f(x)]n = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a (follows from 6)
x→a
√ √
8. lim n x = n a
x→a
√ √
9. lim n f(x) = n lim f(x) (If n is even, we must additionally
x→a x→a
assume that lim f(x) > 0)
x→a
. . . . . .

76. Applying the limit laws
Example
( )
Find lim x2 + 2x + 4 .
x→3
. . . . . .

77. Applying the limit laws
Example
( )
Find lim x2 + 2x + 4 .
x→3
Solution
By applying the limit laws repeatedly:
( )
lim x2 + 2x + 4
x→3
. . . . . .

78. Applying the limit laws
Example
( )
Find lim x2 + 2x + 4 .
x→3
Solution
By applying the limit laws repeatedly:
( ) ( )
lim x2 + 2x + 4 = lim x2 + lim (2x) + lim (4)
x→3 x→3 x→3 x→3
. . . . . .

79. Applying the limit laws
Example
( )
Find lim x2 + 2x + 4 .
x→3
Solution
By applying the limit laws repeatedly:
( ) ( )
lim x2 + 2x + 4 = lim x2 + lim (2x) + lim (4)
x→3 x→3 x→3 x→3
( )2
= lim x + 2 · lim (x) + 4
x→3 x→3
. . . . . .

80. Applying the limit laws
Example
( )
Find lim x2 + 2x + 4 .
x→3
Solution
By applying the limit laws repeatedly:
( ) ( )
lim x2 + 2x + 4 = lim x2 + lim (2x) + lim (4)
x→3 x→3 x→3 x→3
( )2
= lim x + 2 · lim (x) + 4
x→3 x→3
2
= (3) + 2 · 3 + 4
. . . . . .

81. Applying the limit laws
Example
( )
Find lim x2 + 2x + 4 .
x→3
Solution
By applying the limit laws repeatedly:
( ) ( )
lim x2 + 2x + 4 = lim x2 + lim (2x) + lim (4)
x→3 x→3 x→3 x→3
( )2
= lim x + 2 · lim (x) + 4
x→3 x→3
2
= (3) + 2 · 3 + 4
= 9 + 6 + 4 = 19.
. . . . . .

82. Your turn
Example
x2 + 2x + 4
Find lim
x→3 x3 + 11
. . . . . .

83. Your turn
Example
x2 + 2x + 4
Find lim
x→3 x3 + 11
Solution
19 1
The answer is = .
38 2
. . . . . .

84. Direct Substitution Property
Theorem (The Direct Substitution Property)
If f is a polynomial or a rational function and a is in the domain of
f, then
lim f(x) = f(a)
x→a
. . . . . .

85. Outline
Limits and Pathologies
Basic Limits
Limit Laws
The direct substitution property
Limits with Algebra
Two more limit theorems
Two important trigonometric limits
. . . . . .

86. Limits do not see the point! (in a good way)
Theorem
If f(x) = g(x) when x ̸= a, and lim g(x) = L, then lim f(x) = L.
x→a x→a
. . . . . .

87. Limits do not see the point! (in a good way)
Theorem
If f(x) = g(x) when x ̸= a, and lim g(x) = L, then lim f(x) = L.
x→a x→a
Example
x2 + 2x + 1
Find lim , if it exists.
x→−1 x+1
. . . . . .

88. Limits do not see the point! (in a good way)
Theorem
If f(x) = g(x) when x ̸= a, and lim g(x) = L, then lim f(x) = L.
x→a x→a
Example
x2 + 2x + 1
Find lim , if it exists.
x→−1 x+1
Solution
x2 + 2x + 1
Since = x + 1 whenever x ̸= −1, and since
x+1
x2 + 2x + 1
lim x + 1 = 0, we have lim = 0.
x→−1 x→−1 x+1
. . . . . .

89. x2 + 2x + 1
ET game for f(x) =
x+1
y
.
. . x
.
−
. 1
Even if f(−1) were something else, it would not effect the
limit.
. . . . . .

90. x2 + 2x + 1
ET game for f(x) =
x+1
y
.
. . x
.
−
. 1
Even if f(−1) were something else, it would not effect the
limit.
. . . . . .

91. Limit of a function defined piecewise at a boundary
point
Example
Let
{
x2 x≥0
f(x) =
−x x<0
Does lim f(x) exist?
x→0
. . . . . .

92. Limit of a function defined piecewise at a boundary
point
Example
Let
{
x2 x≥0
f(x) =
−x x<0
Does lim f(x) exist?
x→0
Solution
We have
MTP DSP
lim f(x) = lim x2 = 02 = 0
x→0+ x→0+
Likewise:
lim f(x) = lim −x = −0 = 0
x→0− x→0−
So lim f(x) = 0.
x→0
. . . . . .

93. Limit of a function defined piecewise at a boundary
point
Example
Let
{
x2 x≥0 .
f(x) =
−x x<0
Does lim f(x) exist?
x→0
Solution
We have
MTP DSP
lim f(x) = lim x2 = 02 = 0
x→0+ x→0+
Likewise:
lim f(x) = lim −x = −0 = 0
x→0− x→0−
So lim f(x) = 0.
x→0
. . . . . .

94. Finding limits by algebraic manipulations
Example√
x−2
Find lim .
x→4 x−4
. . . . . .

95. Finding limits by algebraic manipulations
Example√
x−2
Find lim .
x→4 x−4
Solution √ √ √
2
Write the denominator as x − 4 = x − 4 = ( x − 2)( x + 2).
. . . . . .

96. Finding limits by algebraic manipulations
Example√
x−2
Find lim .
x→4 x−4
Solution √ 2 √ √
Write the denominator as x − 4 = x − 4 = ( x − 2)( x + 2).
So
√ √
x−2 x−2
lim = lim √ √
x→4 x − 4 x→4 ( x − 2)( x + 2)
1 1
= lim √ =
x→4 x+2 4
. . . . . .

97. Your turn
Example
Let
{
1 − x2 x≥1
f(x) =
2x x<1
Find lim f(x) if it exists.
x→1
. . . . . .

98. Your turn
Example
Let
{
1 − x2 x≥1
f(x) =
2x x<1
Find lim f(x) if it exists.
x→1
Solution
We have
( ) DSP
lim f(x) = lim 1 − x2 = 0
x→1+ x→1+
DSP
lim f(x) = lim (2x) = 2
− −
x→1 x→1
The left- and right-hand limits disagree, so the limit does not exist.
. . . . . .

99. Your turn
Example .
Let
{
1 − x2 x≥1
f(x) =
2x x<1 . .
Find lim f(x) if it exists. 1
.
x→1
Solution
We have
( ) DSP
lim f(x) = lim 1 − x2 = 0
x→1+ x→1+
DSP
lim f(x) = lim (2x) = 2
− −
x→1 x→1
The left- and right-hand limits disagree, so the limit does not exist.
. . . . . .

100. Two More Important Limit Theorems
Theorem
If f(x) ≤ g(x) when x is near a (except possibly at a), then
lim f(x) ≤ lim g(x)
x→a x→a
(as usual, provided these limits exist).
Theorem (The Squeeze/Sandwich/Pinching Theorem)
If f(x) ≤ g(x) ≤ h(x) when x is near a (as usual, except possibly at
a), and
lim f(x) = lim h(x) = L,
x→a x→a
then
lim g(x) = L.
x→a
. . . . . .

101. We can use the Squeeze Theorem to make complicated limits
simple.
. . . . . .

102. We can use the Squeeze Theorem to make complicated limits
simple.
Example (π )
Show that lim x2 sin = 0.
x→0 x
. . . . . .

103. We can use the Squeeze Theorem to make complicated limits
simple.
Example (π )
Show that lim x2 sin = 0.
x→0 x
Solution
We have for all x,
(π )
−x2 ≤ x2 sin ≤ x2
x
The left and right sides go to zero as x → 0.
. . . . . .

104. Illustration of the Squeeze Theorem
y
. . (x) = x2
h
. x
.
. . . . . .

105. Illustration of the Squeeze Theorem
y
. . (x) = x2
h
. x
.
.(x) = −x2
f
. . . . . .

106. Illustration of the Squeeze Theorem
y
. . (x) = x2
h
( )
2 1
g
. (x) = x sin
x
. x
.
.(x) = −x2
f
. . . . . .

107. Outline
Limits and Pathologies
Basic Limits
Limit Laws
The direct substitution property
Limits with Algebra
Two more limit theorems
Two important trigonometric limits
. . . . . .

108. Two important trigonometric limits
Theorem
The following two limits hold:
sin θ
lim =1
θ→0 θ
cos θ − 1
lim =0
θ→0 θ
. . . . . .

109. Proof of the Sine Limit
Proof.
Notice
θ
.
θ
.
θ
.
1
.
. . . . . .

110. Proof of the Sine Limit
Proof.
Notice
sin θ ≤ θ
s
. in θ .
θ
.
θ
.
c
. os θ 1
.
. . . . . .

111. Proof of the Sine Limit
Proof.
Notice
sin θ ≤ θ tan θ
. in θ . .an θ
s θ t
.
θ
.
c
. os θ 1
.
. . . . . .

112. Proof of the Sine Limit
Proof.
Notice
θ
sin θ ≤ θ ≤ 2 tan ≤ tan θ
2
. in θ . .an θ
s θ t
.
θ
.
c
. os θ 1
.
. . . . . .

113. Proof of the Sine Limit
Proof.
Notice
θ
sin θ ≤ θ ≤ 2 tan ≤ tan θ
2
Divide by sin θ:
θ 1
1≤ ≤
sin θ cos θ
. in θ . .an θ
s θ t
.
θ
.
c
. os θ 1
.
. . . . . .

114. Proof of the Sine Limit
Proof.
Notice
θ
sin θ ≤ θ ≤ 2 tan ≤ tan θ
2
Divide by sin θ:
θ 1
1≤ ≤
sin θ cos θ
. in θ . .an θ
s θ t
.
θ Take reciprocals:
.
c
. os θ 1
. sin θ
1≥ ≥ cos θ
θ
. . . . . .

115. Proof of the Sine Limit
Proof.
Notice
θ
sin θ ≤ θ ≤ 2 tan ≤ tan θ
2
Divide by sin θ:
θ 1
1≤ ≤
sin θ cos θ
. in θ . .an θ
s θ t
.
θ Take reciprocals:
.
c
. os θ 1
. sin θ
1≥ ≥ cos θ
θ
As θ → 0, the left and right sides tend to 1. So, then, must the
middle expression.
. . . . . .

116. Proof of the Cosine Limit
Proof.
1 − cos θ 1 − cos θ 1 + cos θ 1 − cos2 θ
= · =
θ θ 1 + cos θ θ(1 + cos θ)
sin2 θ sin θ sin θ
= = ·
θ(1 + cos θ) θ 1 + cos θ
So
( ) ( )
1 − cos θ sin θ sin θ
lim = lim · lim
θ→0 θ θ→0 θ θ→0 1 + cos θ
= 1 · 0 = 0.
. . . . . .

117. Try these
Example
tan θ
lim
θ→0 θ
sin 2θ
lim
θ→0 θ
. . . . . .

118. Try these
Example
tan θ
lim
θ→0 θ
sin 2θ
lim
θ→0 θ
Answer
1
2
. . . . . .