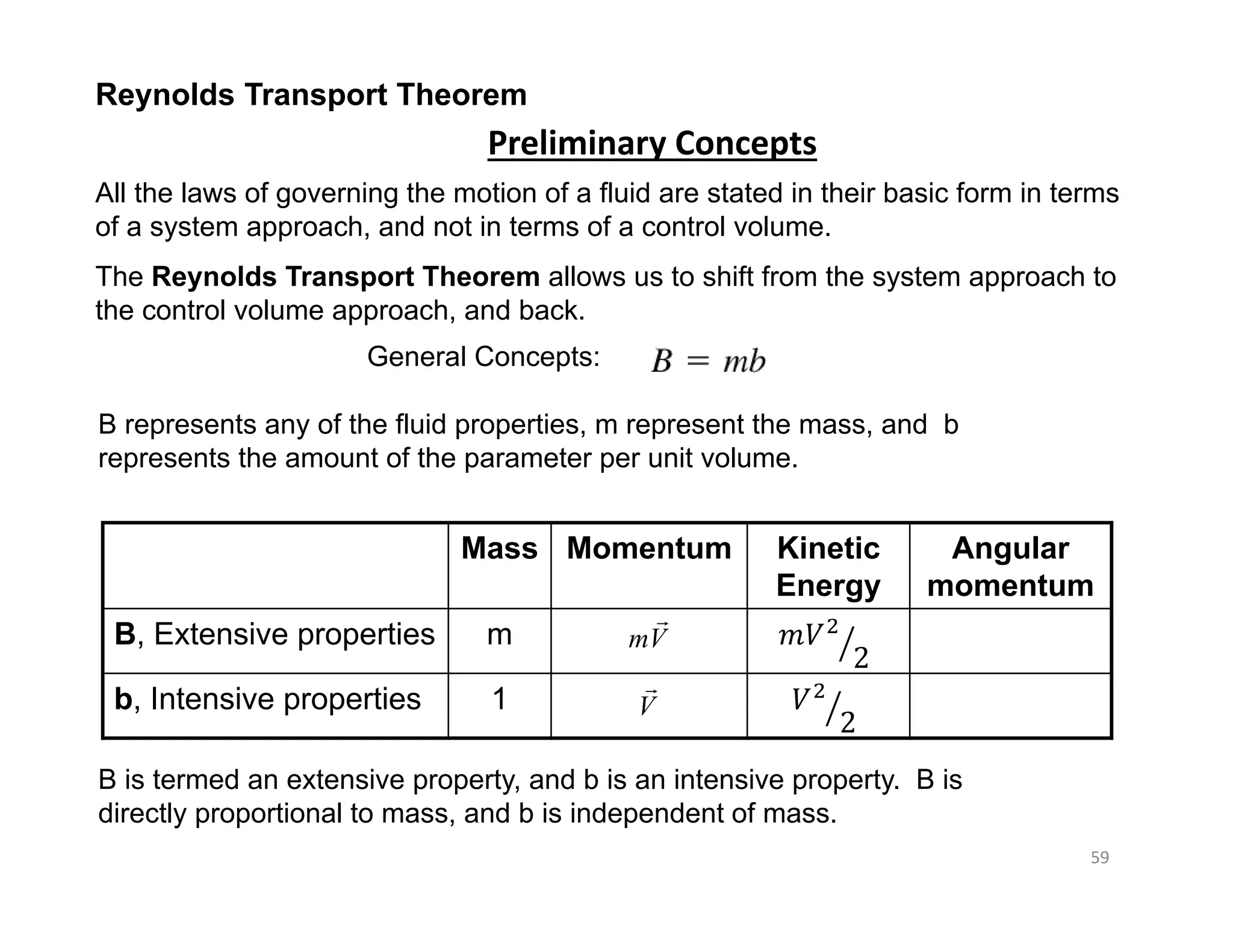
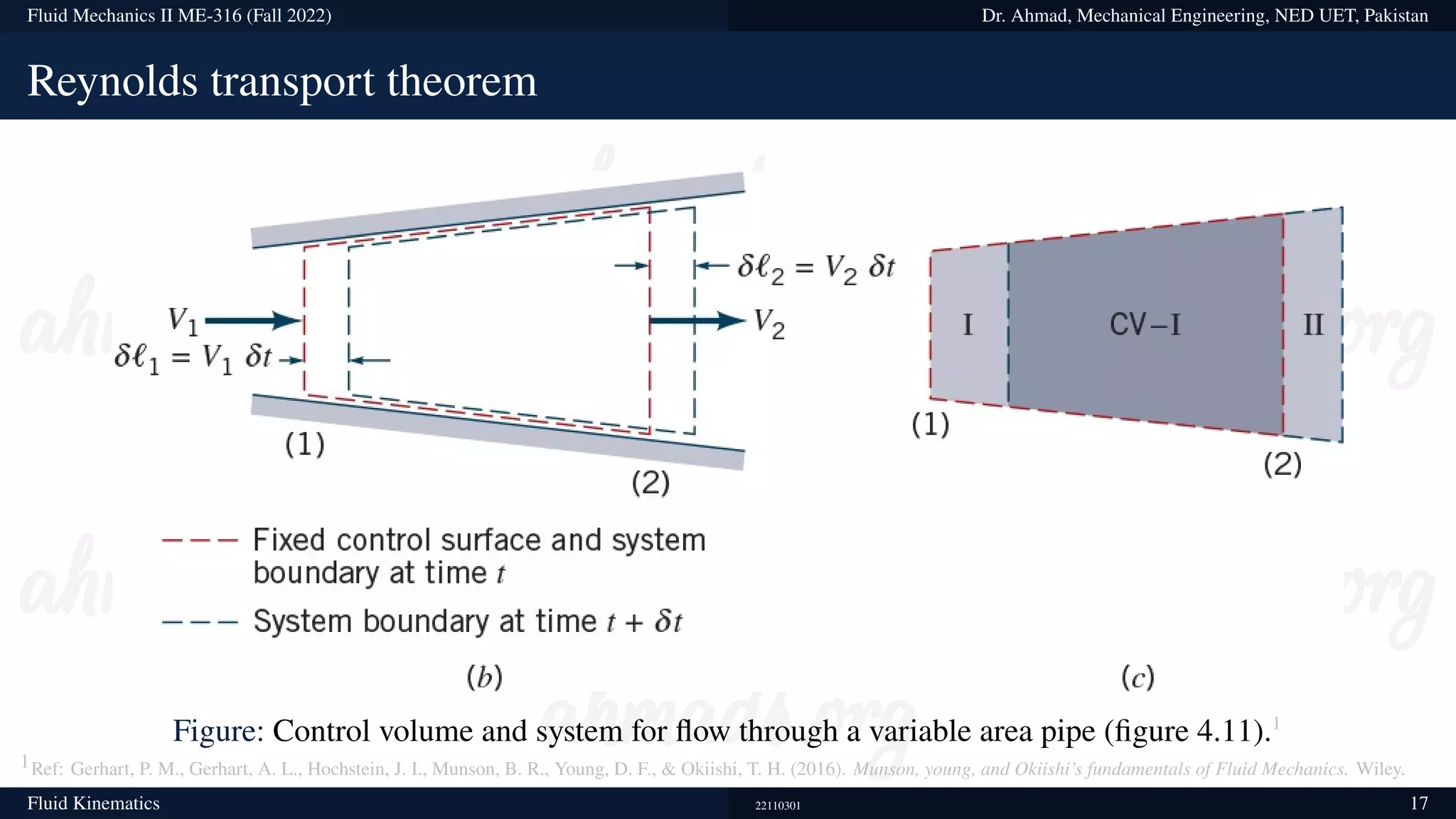
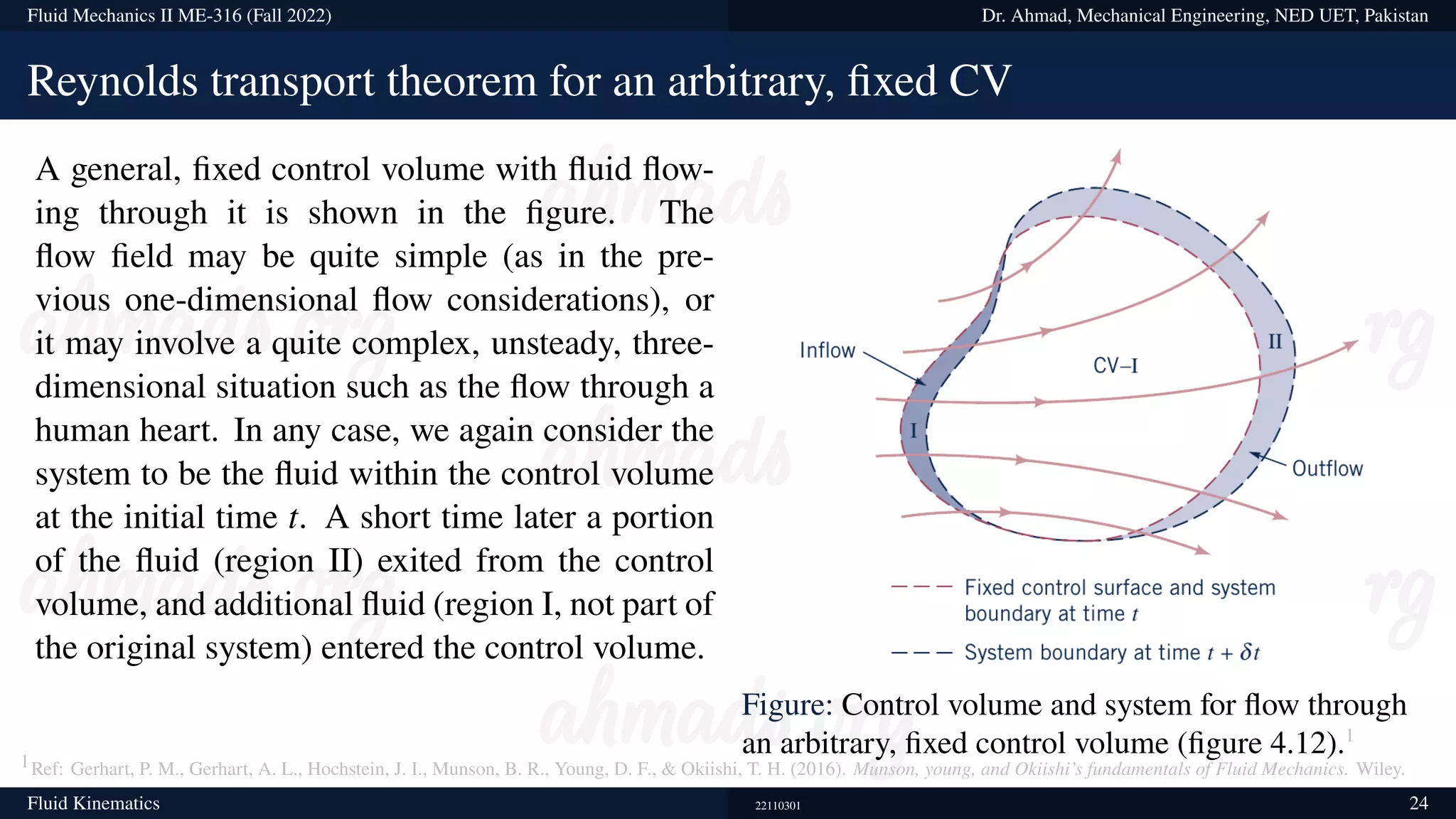
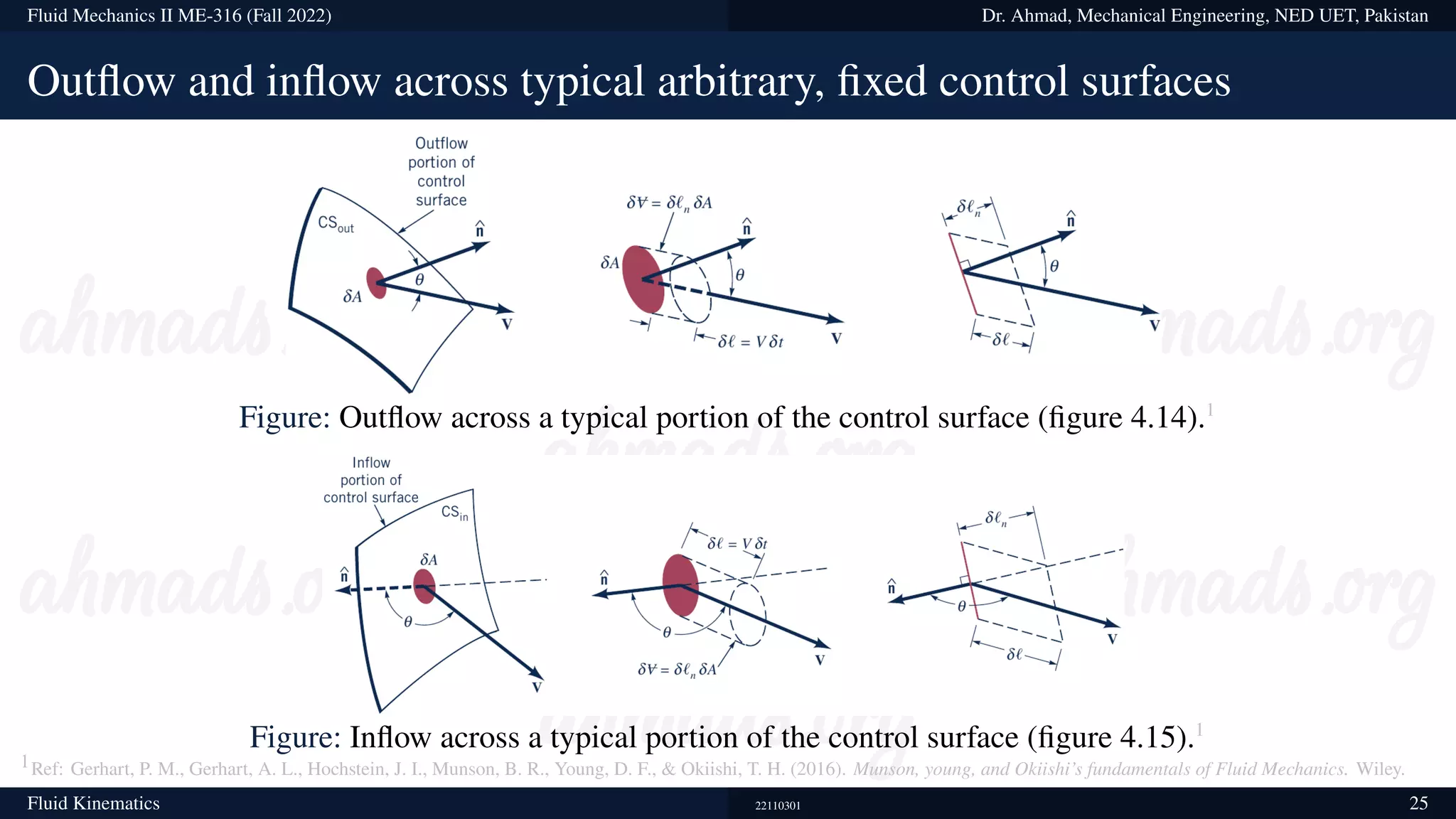
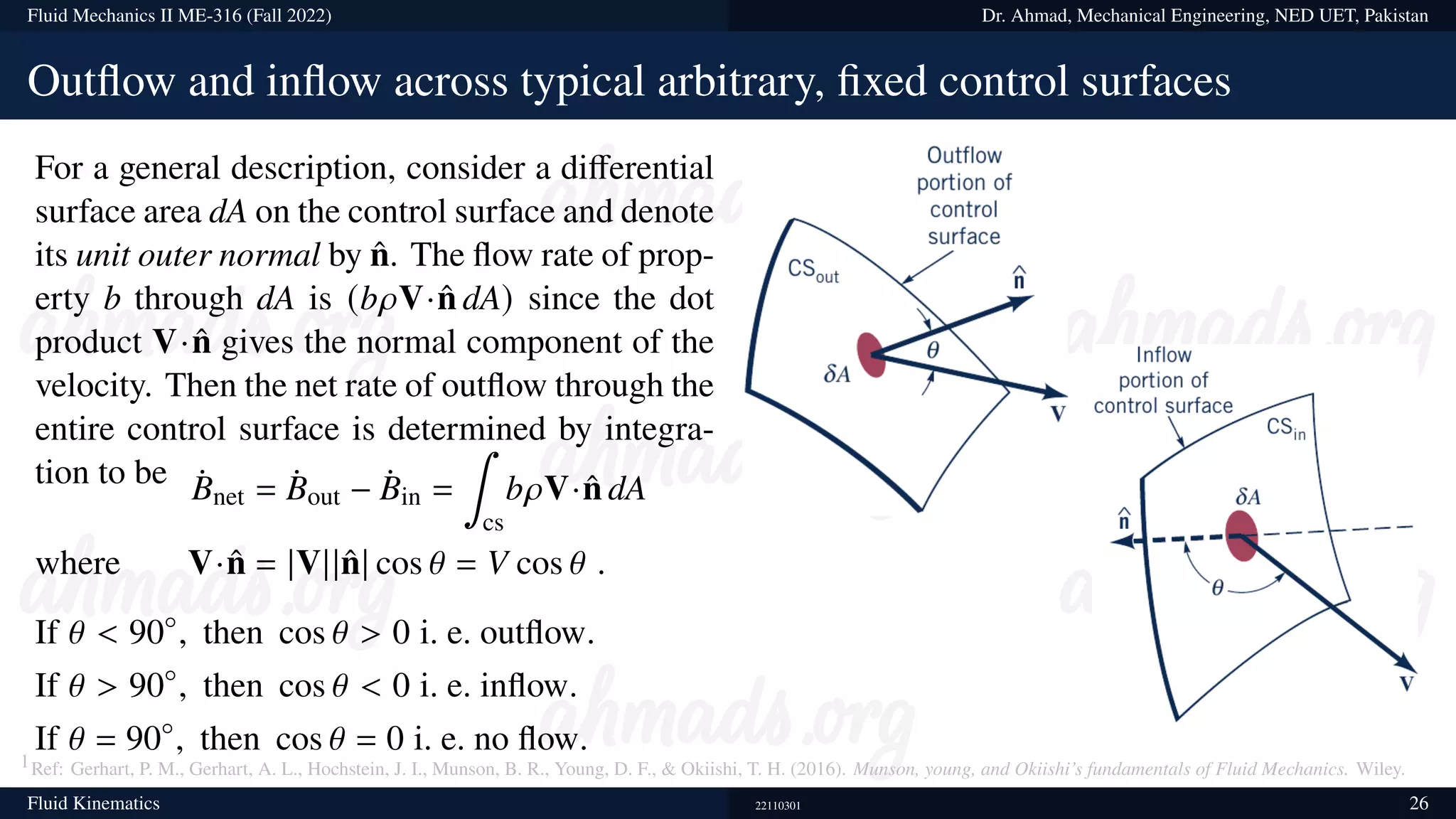
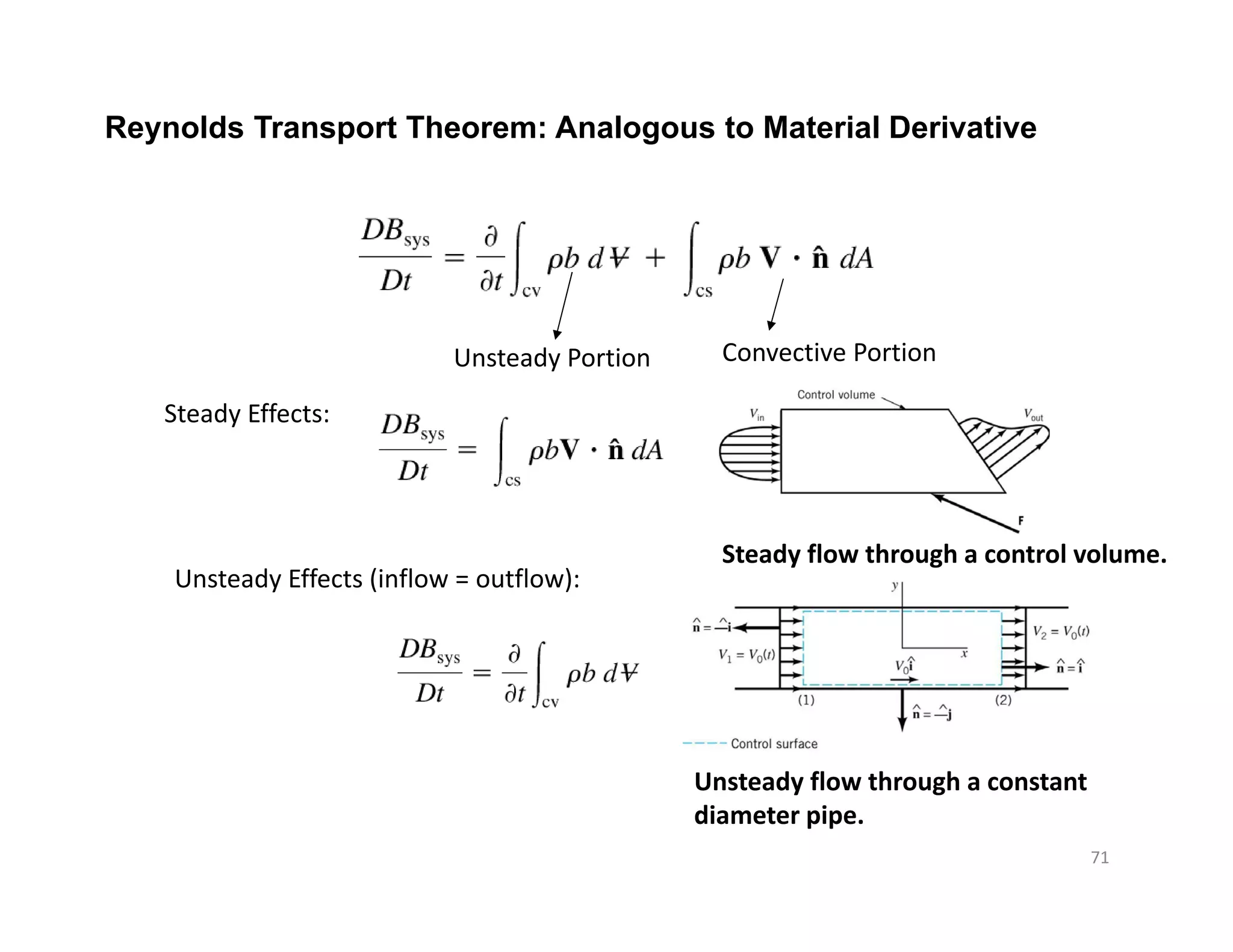
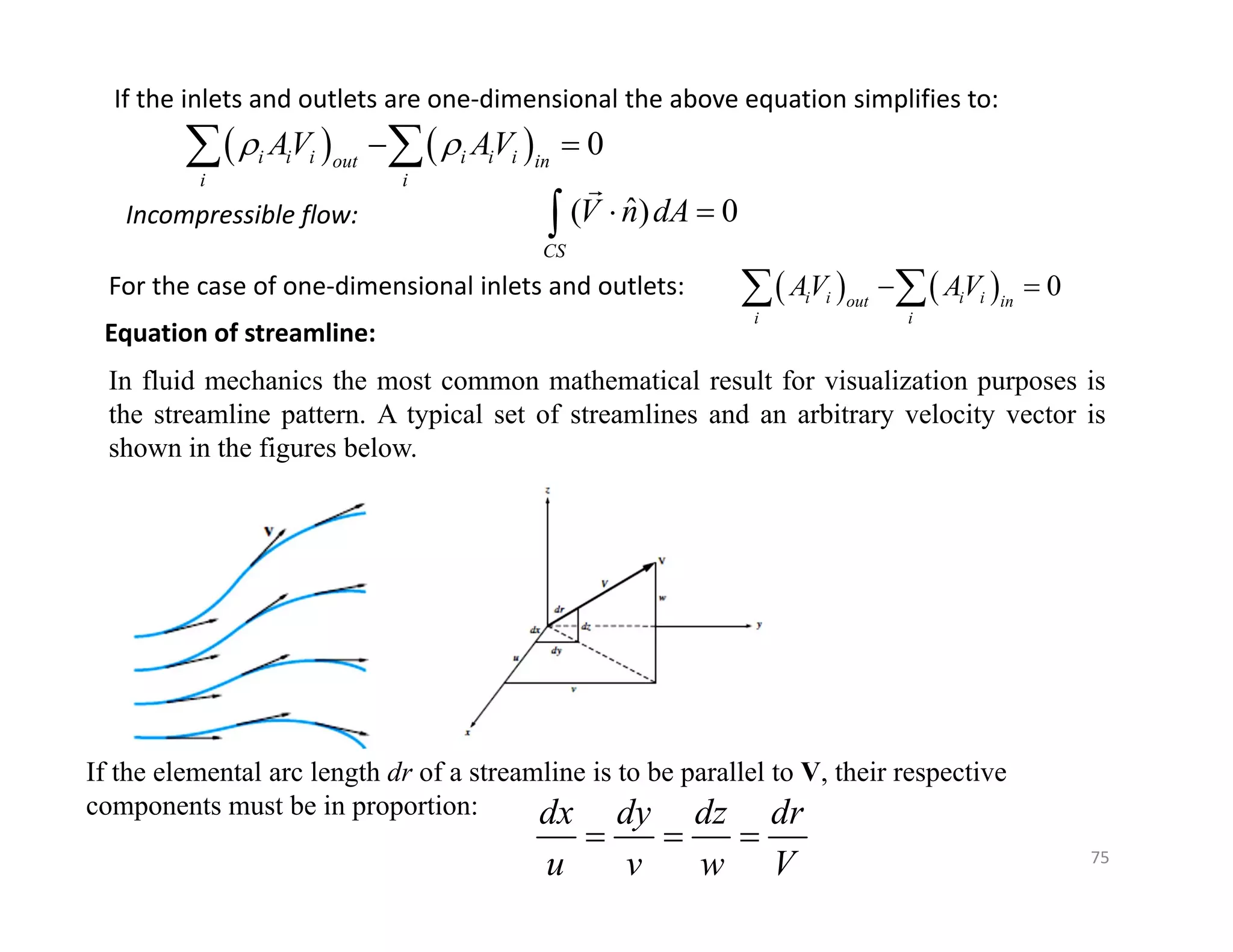
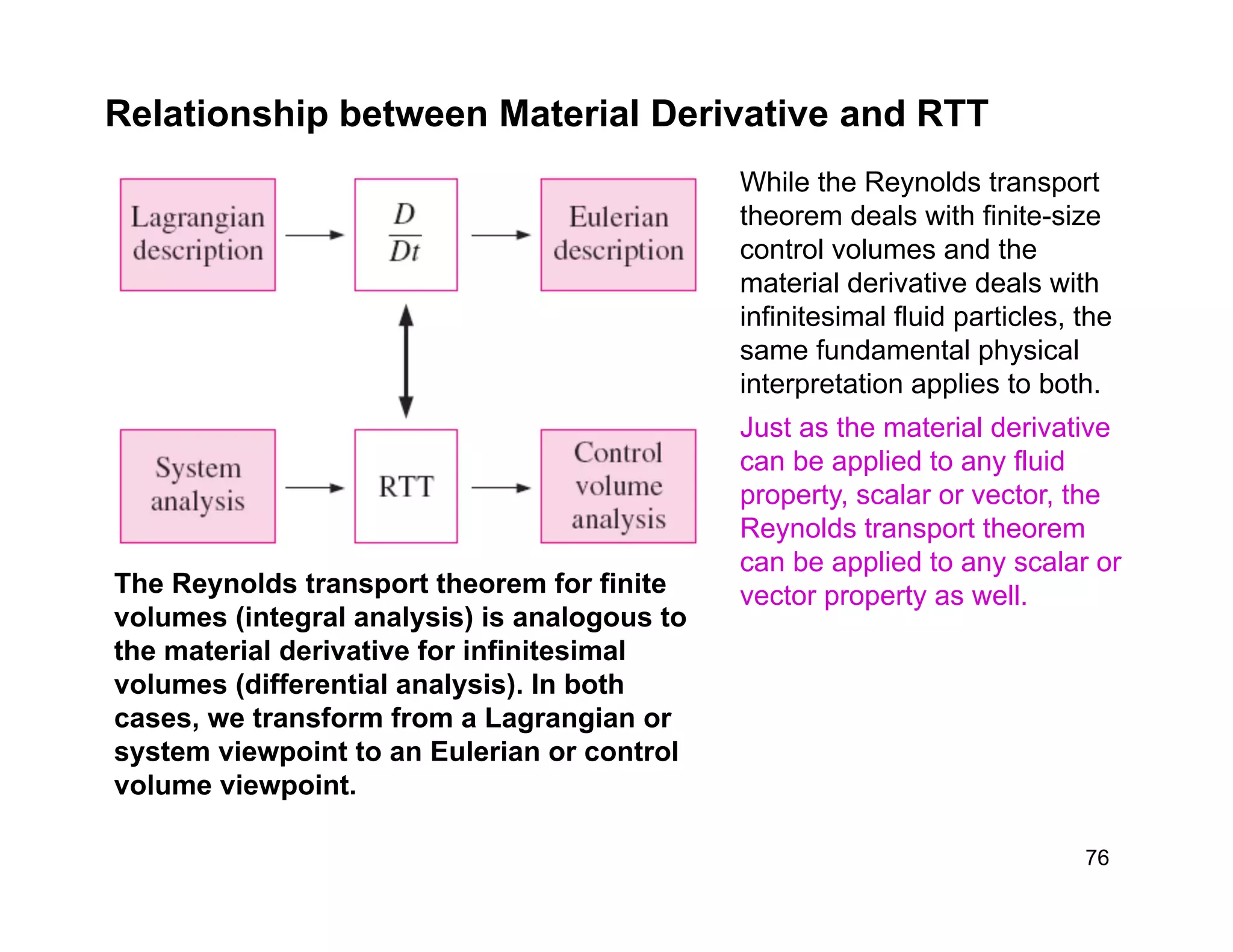
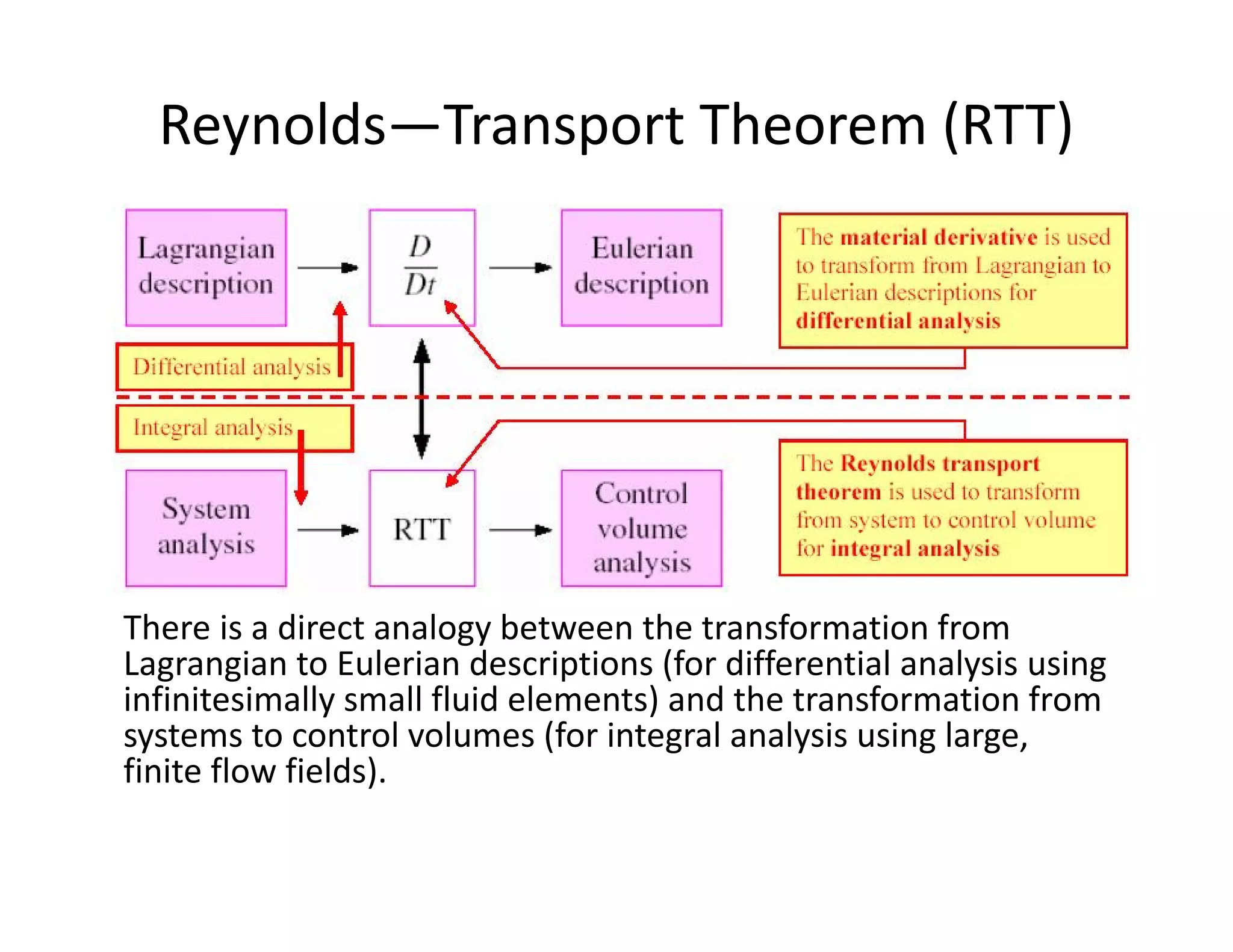
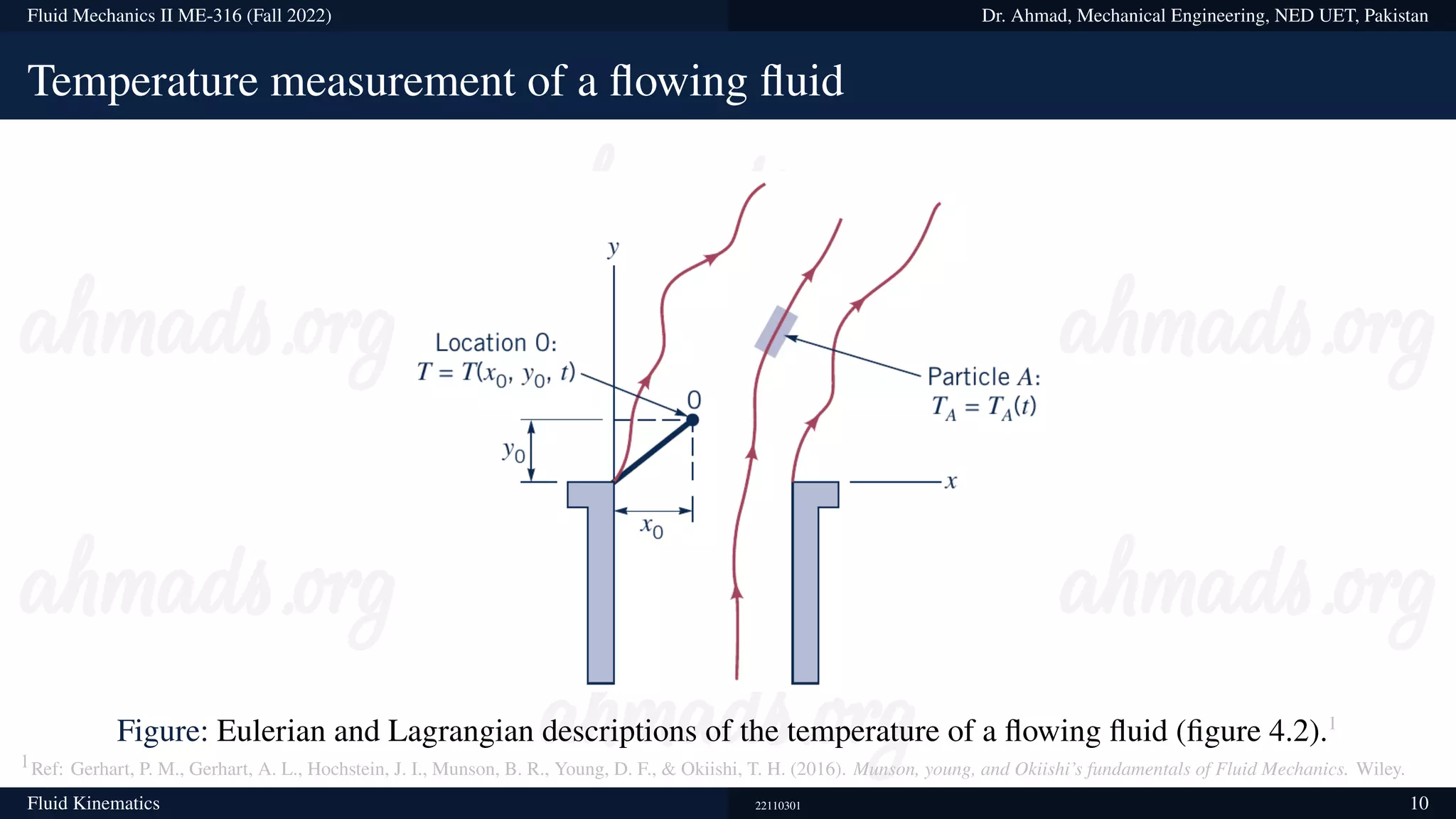
This document contains information about a fluid mechanics course titled "Fluid Mechanics II" taught by Dr. Syed Ahmad Raza at NED University of Engineering & Technology in Pakistan. It discusses the objectives of studying fluid kinematics, which include describing fluid motion using Lagrangian and Eulerian frameworks and visualizing flow fields. Key concepts covered are velocity fields, acceleration fields, control volumes, the Reynolds transport theorem, and distinguishing between kinematics and dynamics. Examples are provided of different ways to analyze fluid temperature and flow patterns using Lagrangian and Eulerian descriptions.










![12
FLOW PATTERNS AND FLOW VISUALIZATION
Spinning baseball. The late F. N. M.
Brown devoted many years to developing
and using smoke visualization in wind
tunnels at the University of Notre Dame.
Here the flow speed is about 23 m/s and
the ball is rotated at 630 rpm.
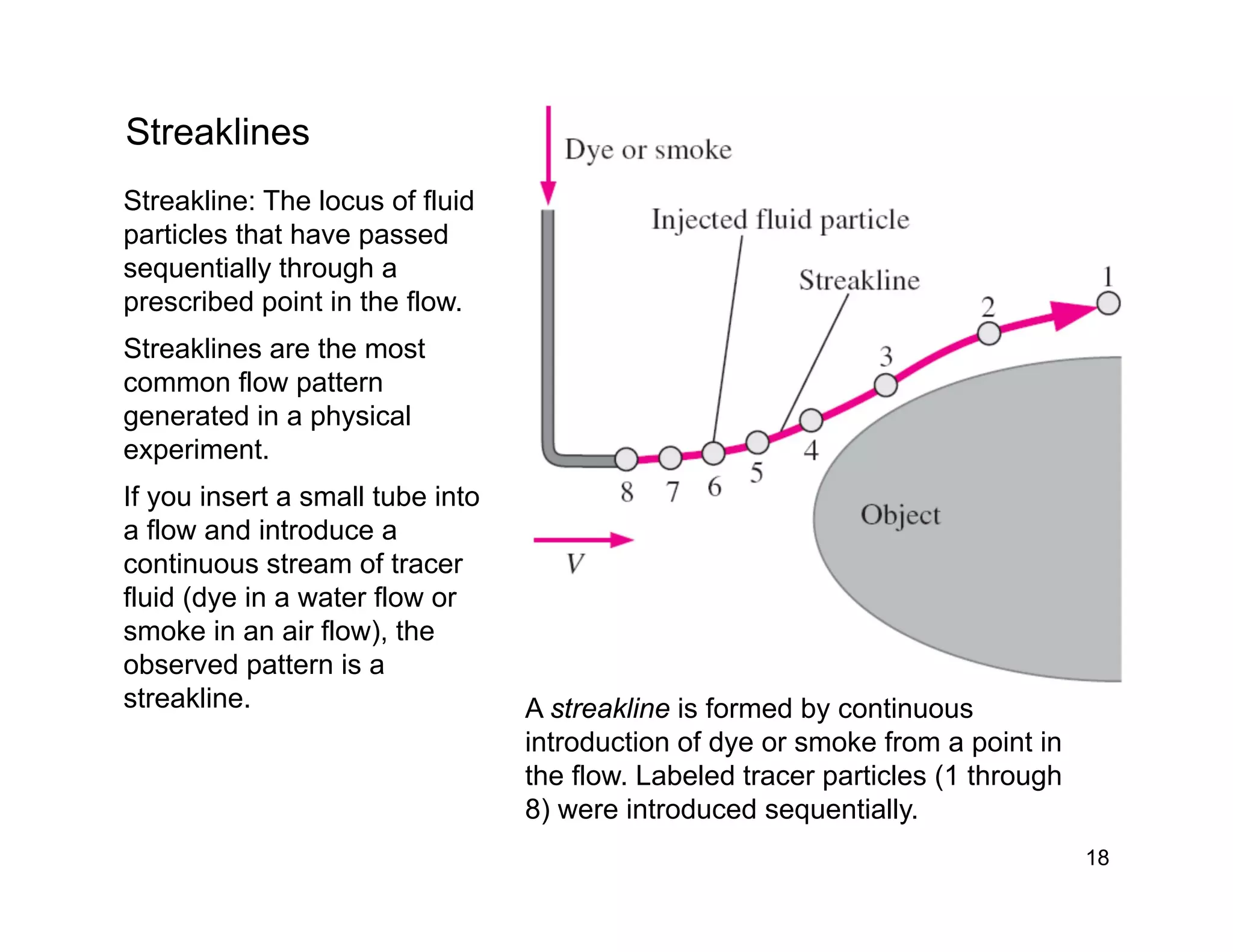
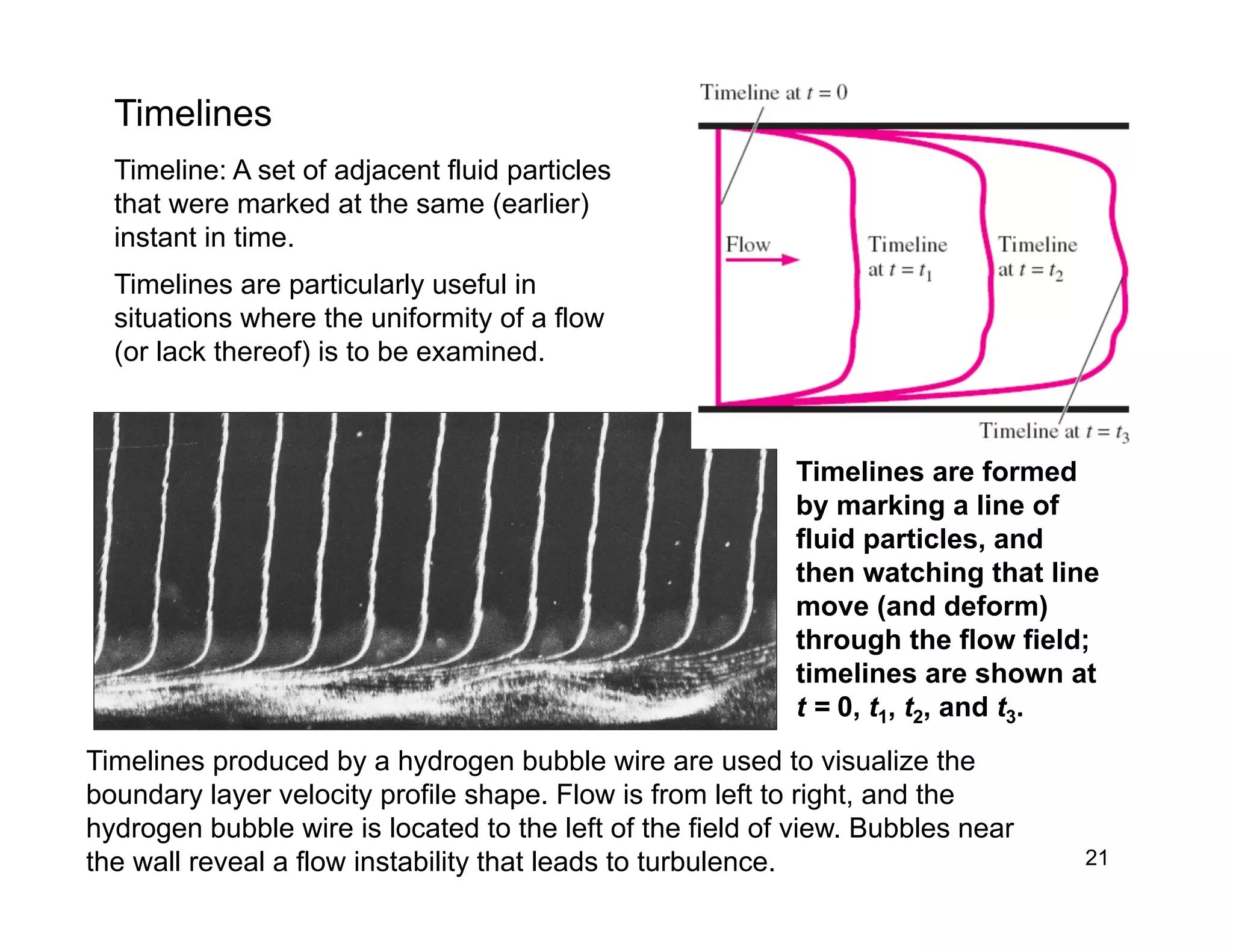
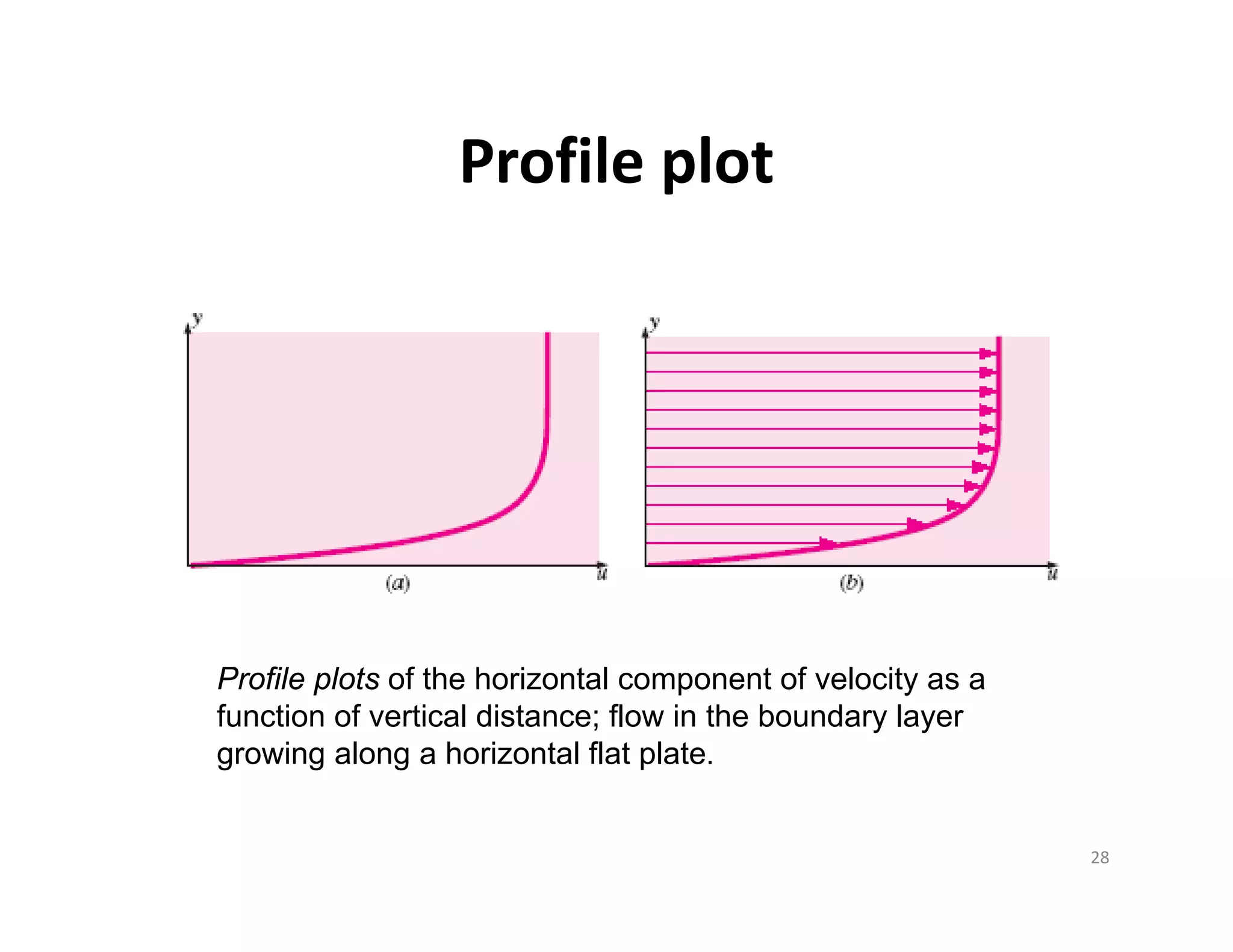
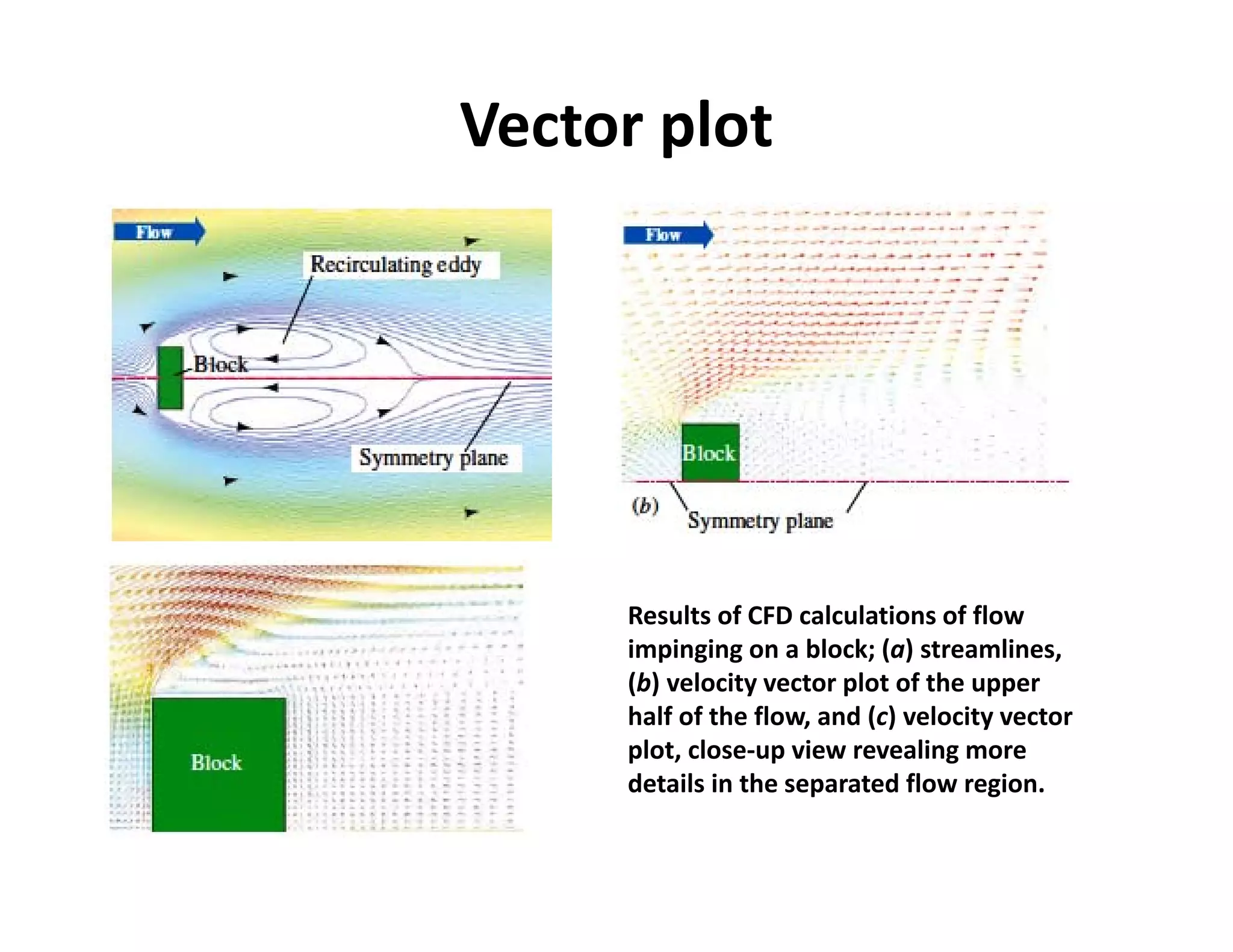
• Flow visualization: The visual
examination of flow field
features.
• While quantitative study of fluid
dynamics requires advanced
mathematics, much can be
learned from flow visualization.
• Flow visualization is useful not
only in physical experiments but
in numerical solutions as well
[computational fluid
dynamics (CFD)].
• In fact, the very first thing an
engineer using CFD does after
obtaining a numerical solution is
simulate some form of flow
visualization, so that he or she
can see the whole picture rather
than merely a list of numbers
and quantitative data.](https://image.slidesharecdn.com/lecture2-221119135350-3cba5df4/75/lecture-2-pdf-12-2048.jpg)








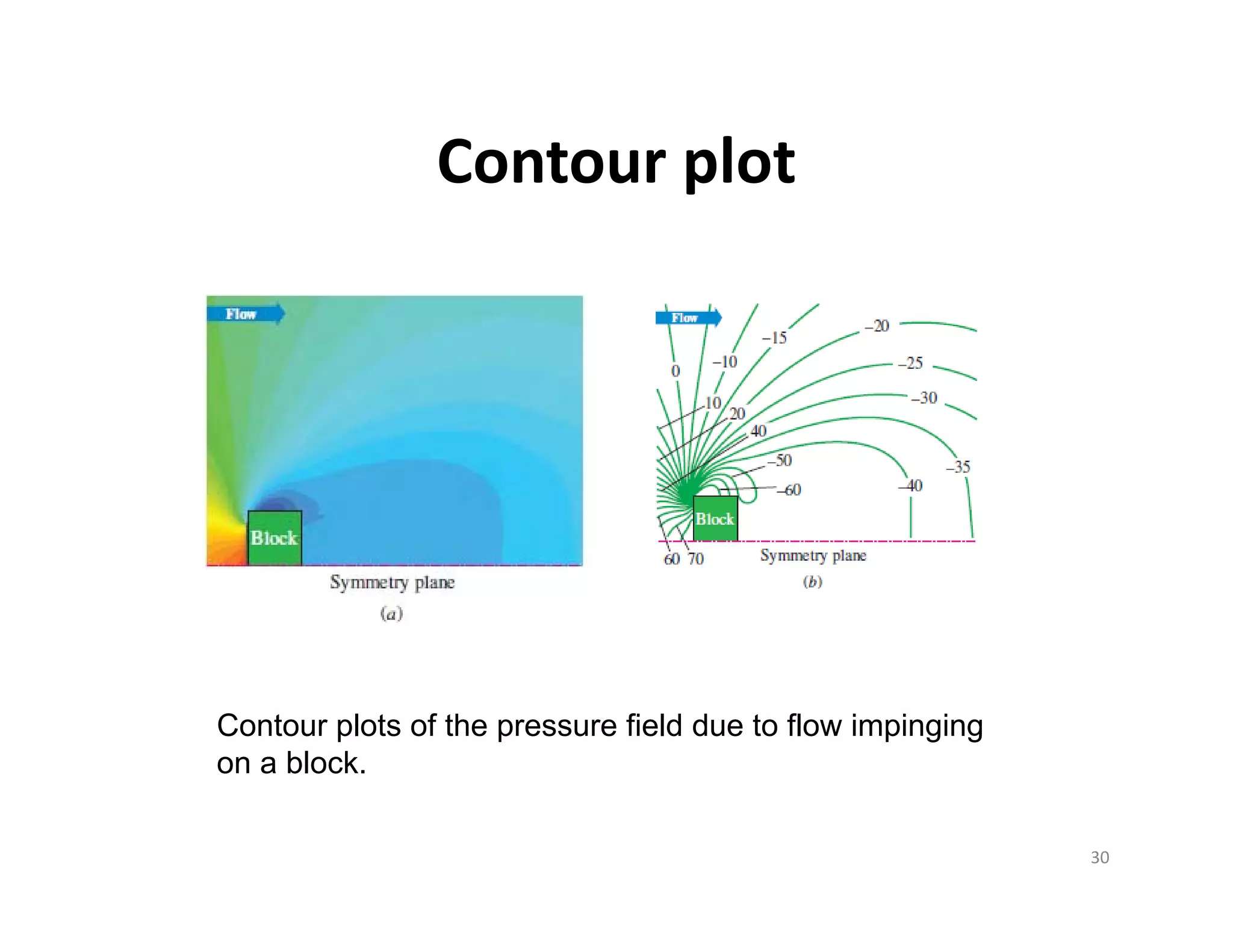



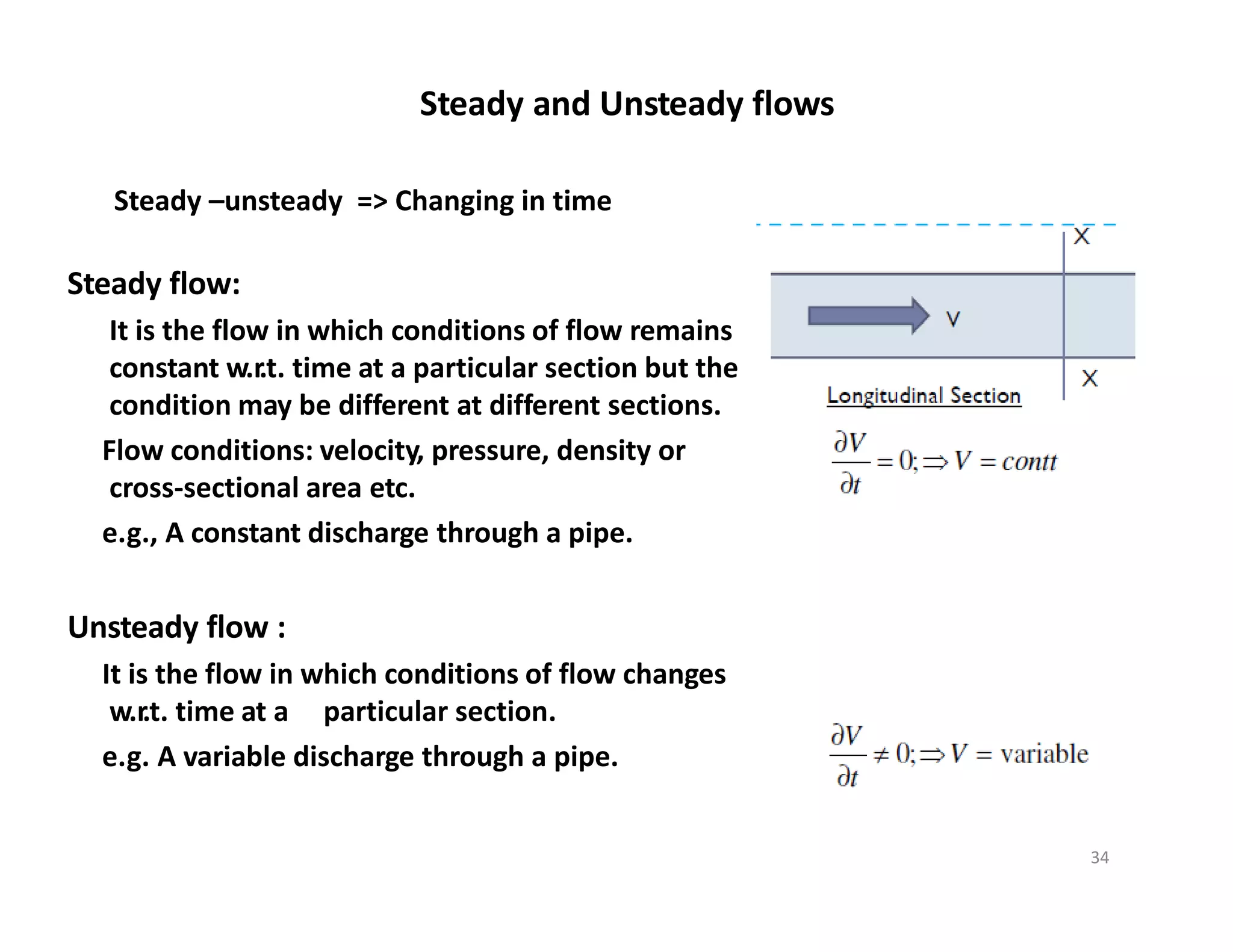


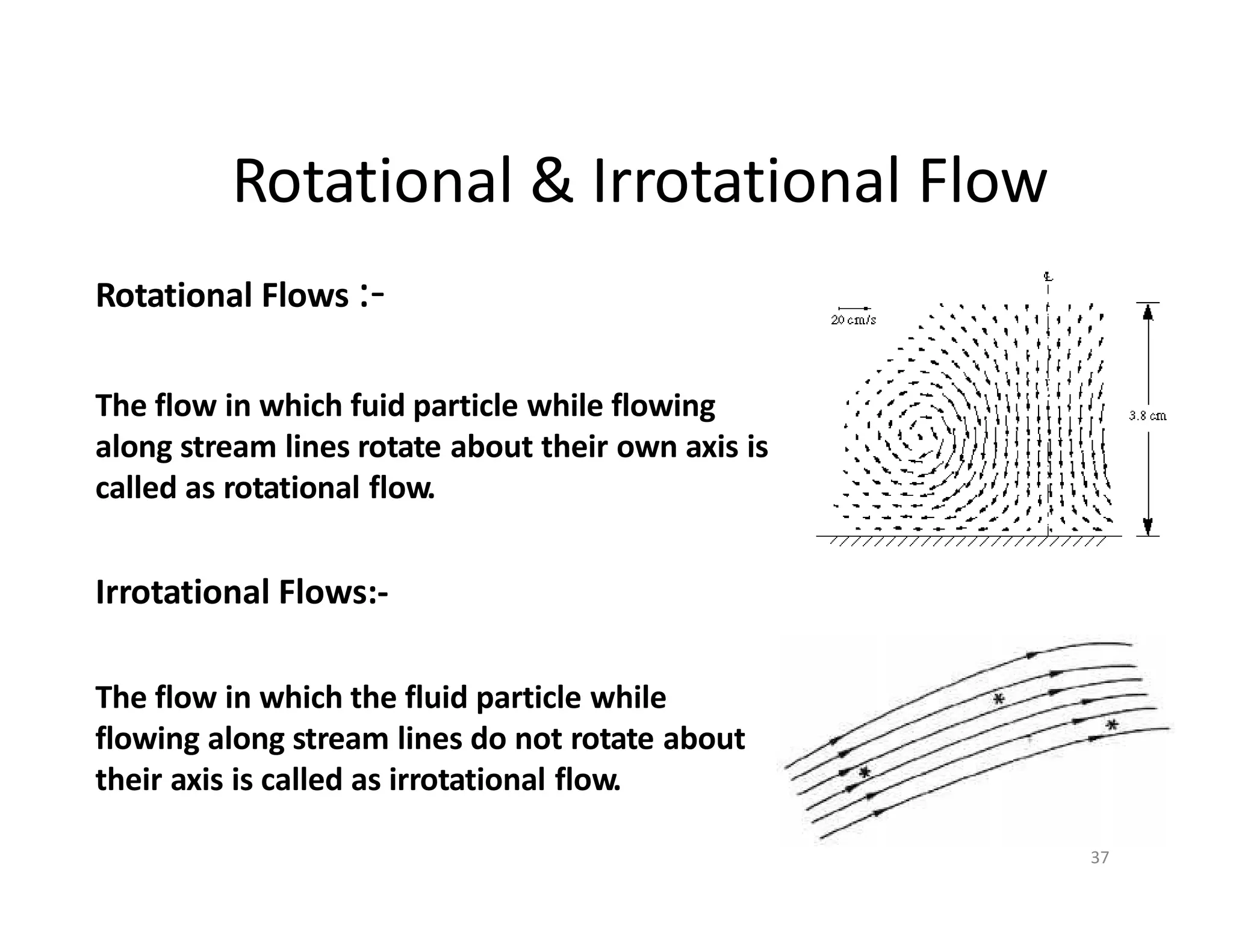

![Fluid Mechanics II ME-316 (Fall 2022) Dr. Ahmad, Mechanical Engineering, NED UET, Pakistan
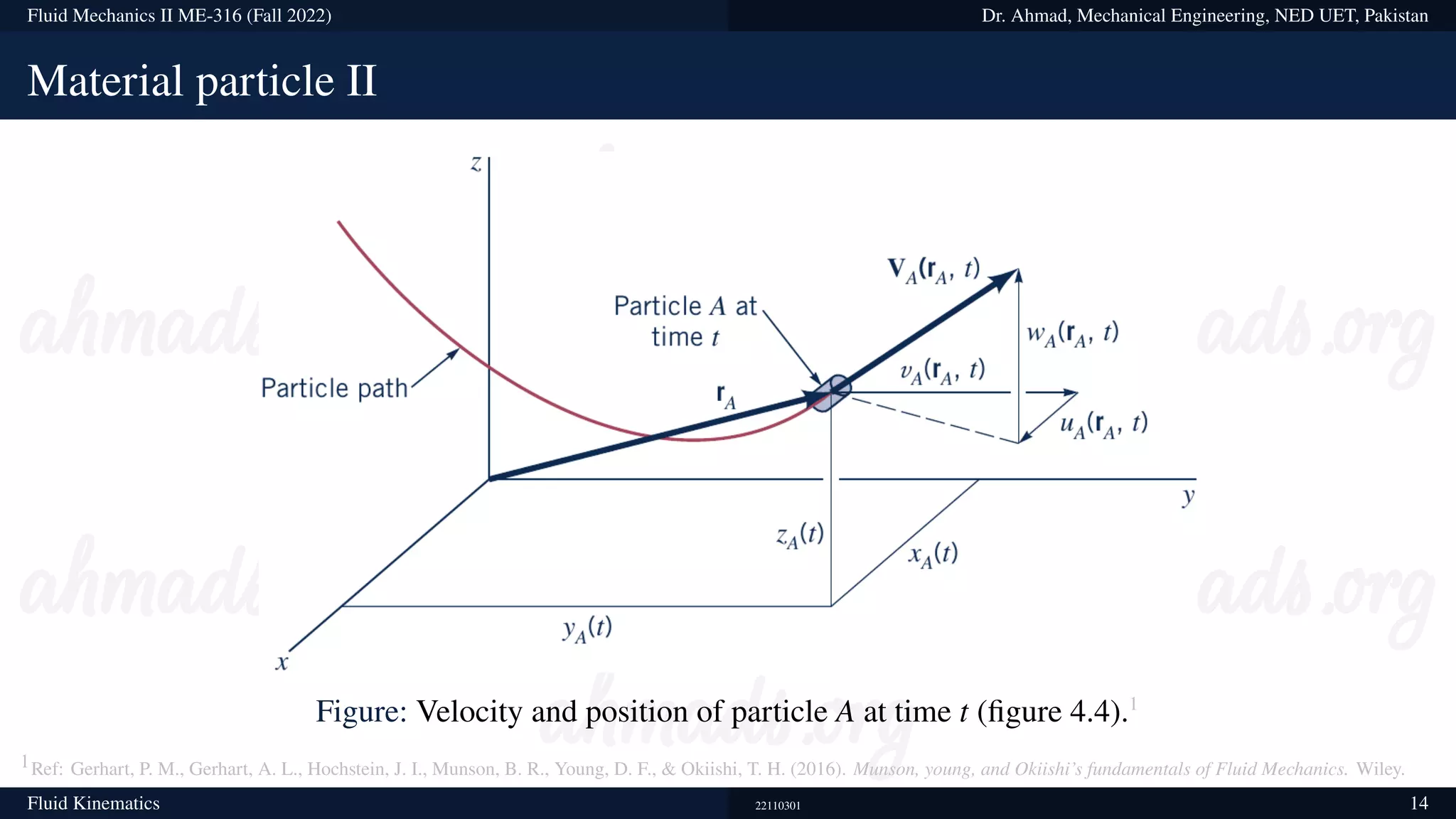
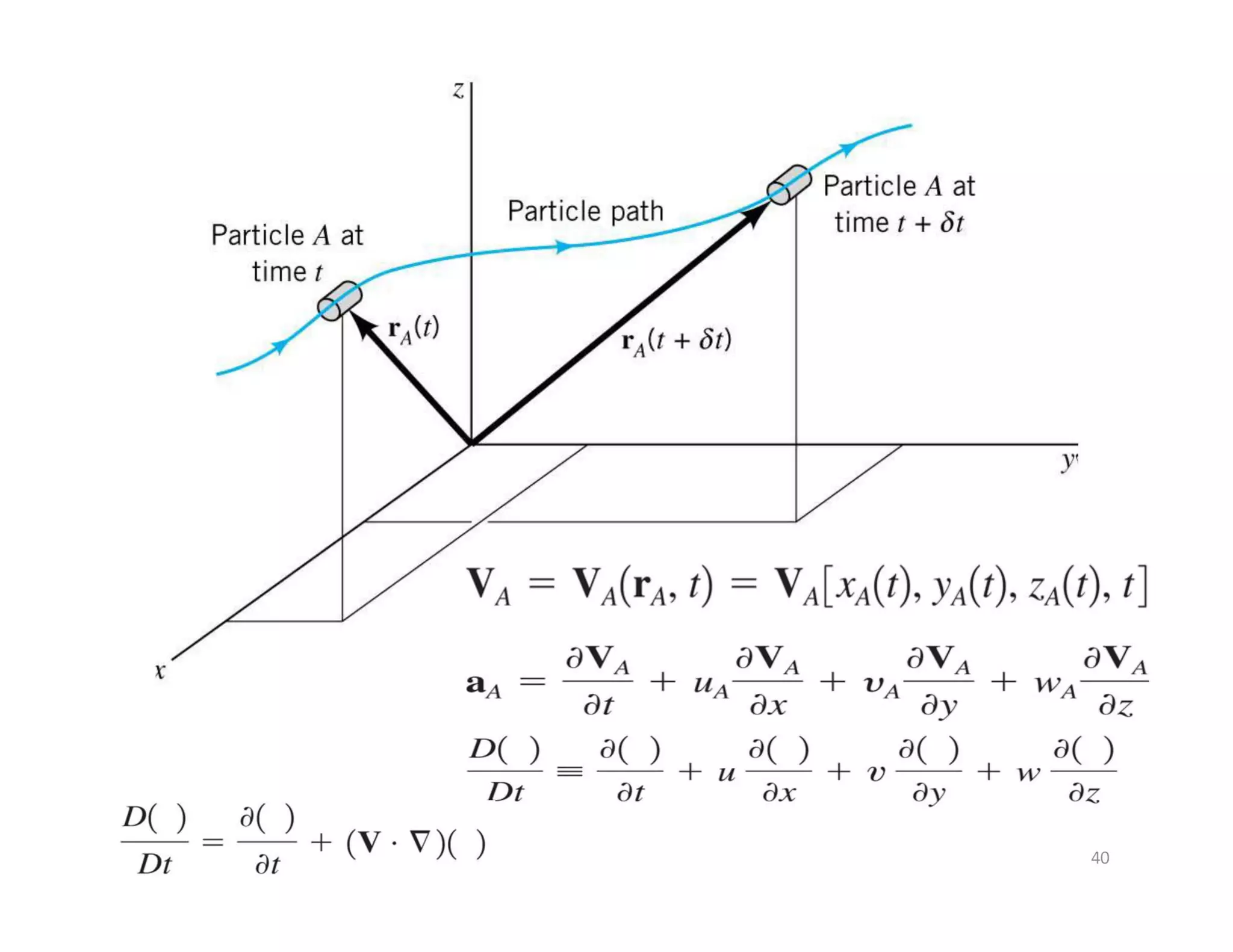
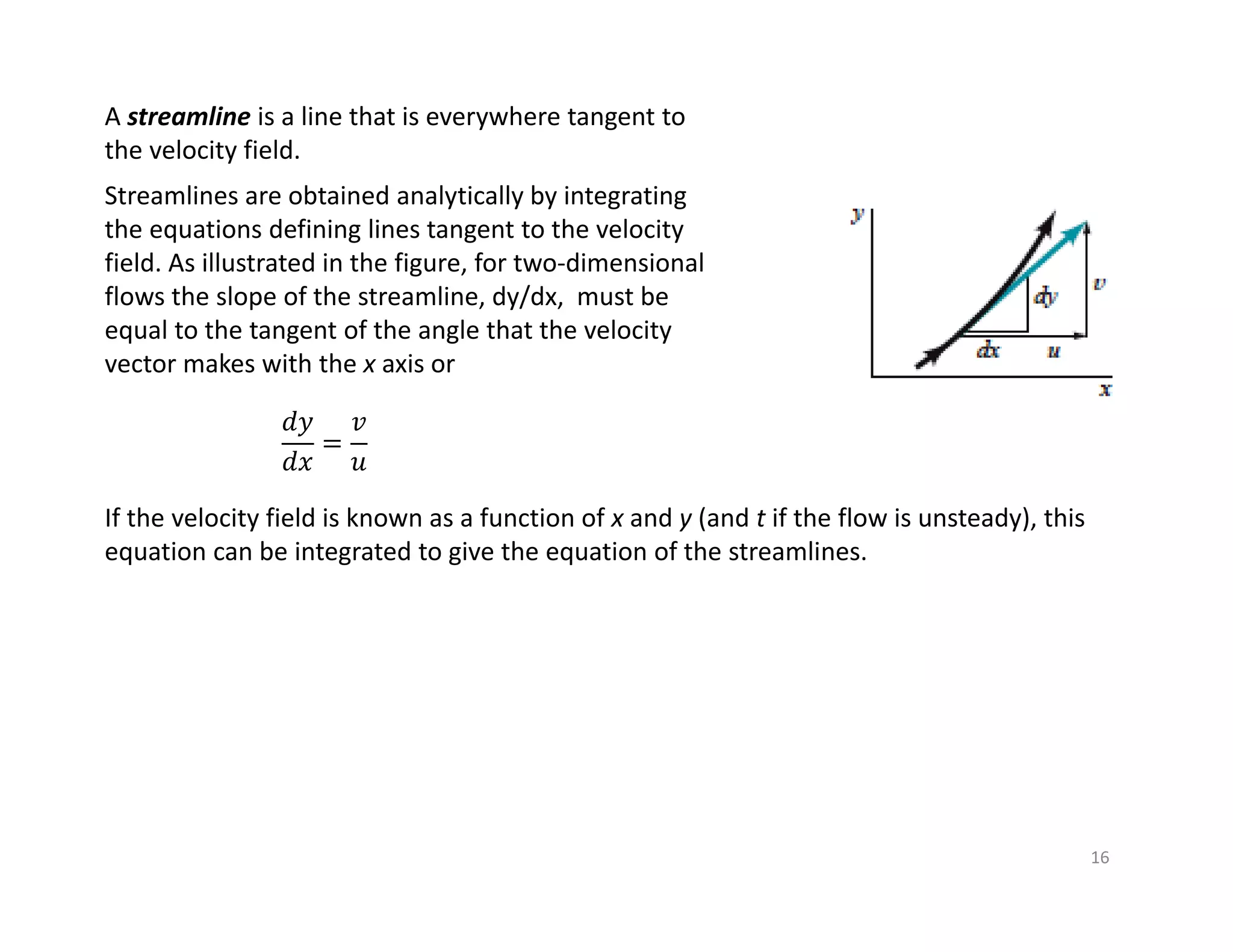
Material particle I
The equations of motion for fluid flow (such as Newton’s second law) can be written for a fluid
particle, which we also call a material particle. If we were to follow a particular fluid particle,
particle A, as it moves around in the flow, we would be employing the Lagrangian description, and
the equations of motion would be directly applicable. For example, we would define the particle A’s
location in space in terms of a material position vector,
rA = rA(t) = xA(t)î + yA(t)ĵ + zA(t)k̂ .
Similarly, the velocity vector for the particle A would be defined as
VA = VA(rA, t) = VA[(xA, t), (yA, t), (zA, t)] .
However, some mathematical manipulation is then necessary to convert the equations of motion into
forms applicable to the Eulerian description.
Fluid Kinematics 22110301 13](https://image.slidesharecdn.com/lecture2-221119135350-3cba5df4/75/lecture-2-pdf-36-2048.jpg)