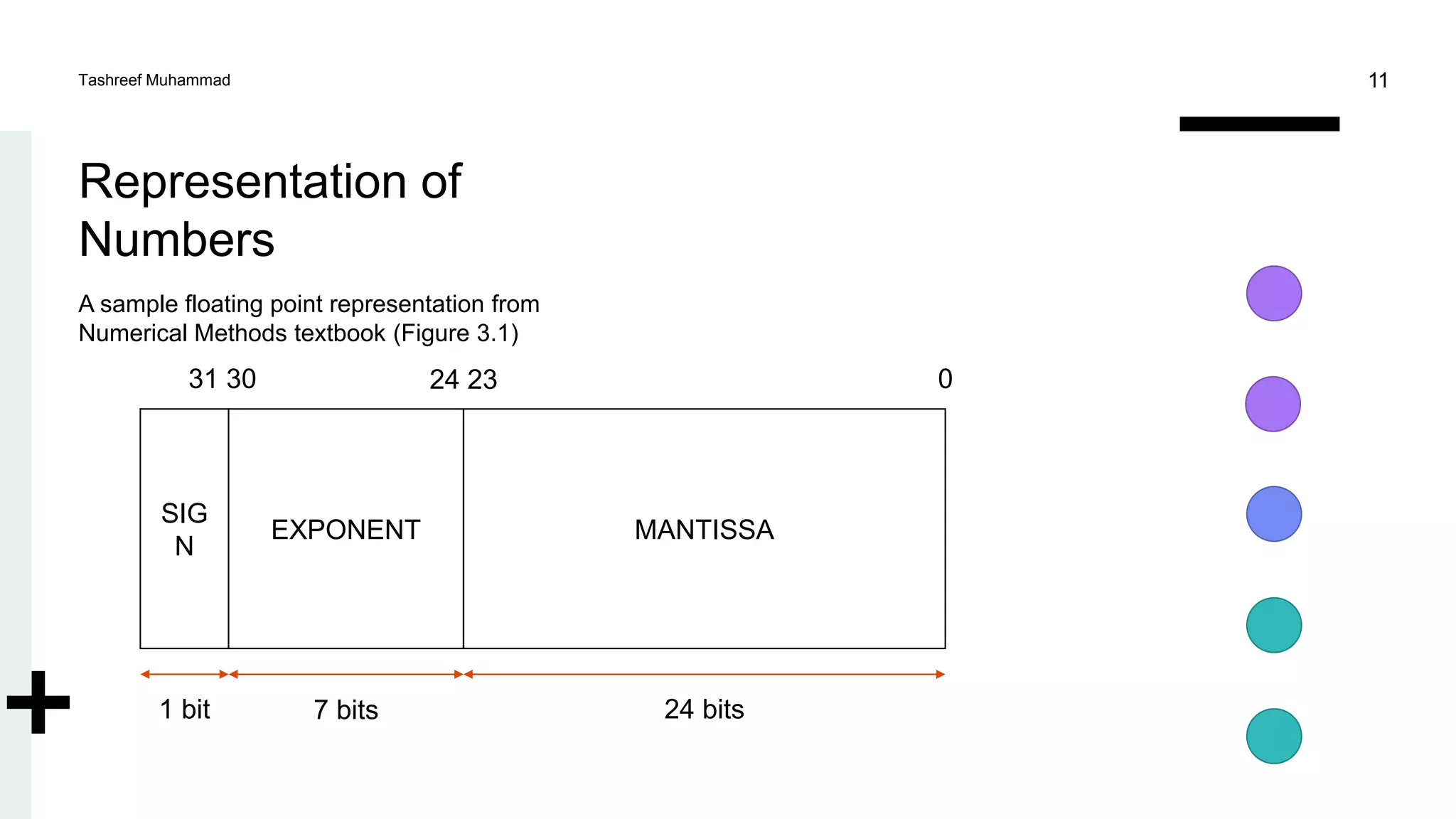
The document provides an overview of numerical methods focused on the representation of numerical values in computers, including various number systems (decimal, binary, hexadecimal) and methods for number conversion. It discusses how modern computers store numbers, the representation of integers and floating-point numbers, and the arithmetic operations involved, while also addressing potential errors in arithmetic and implications on mathematical laws. Key topics include computer arithmetic, normalization of floating-point numbers, and examples illustrating errors and calculations.