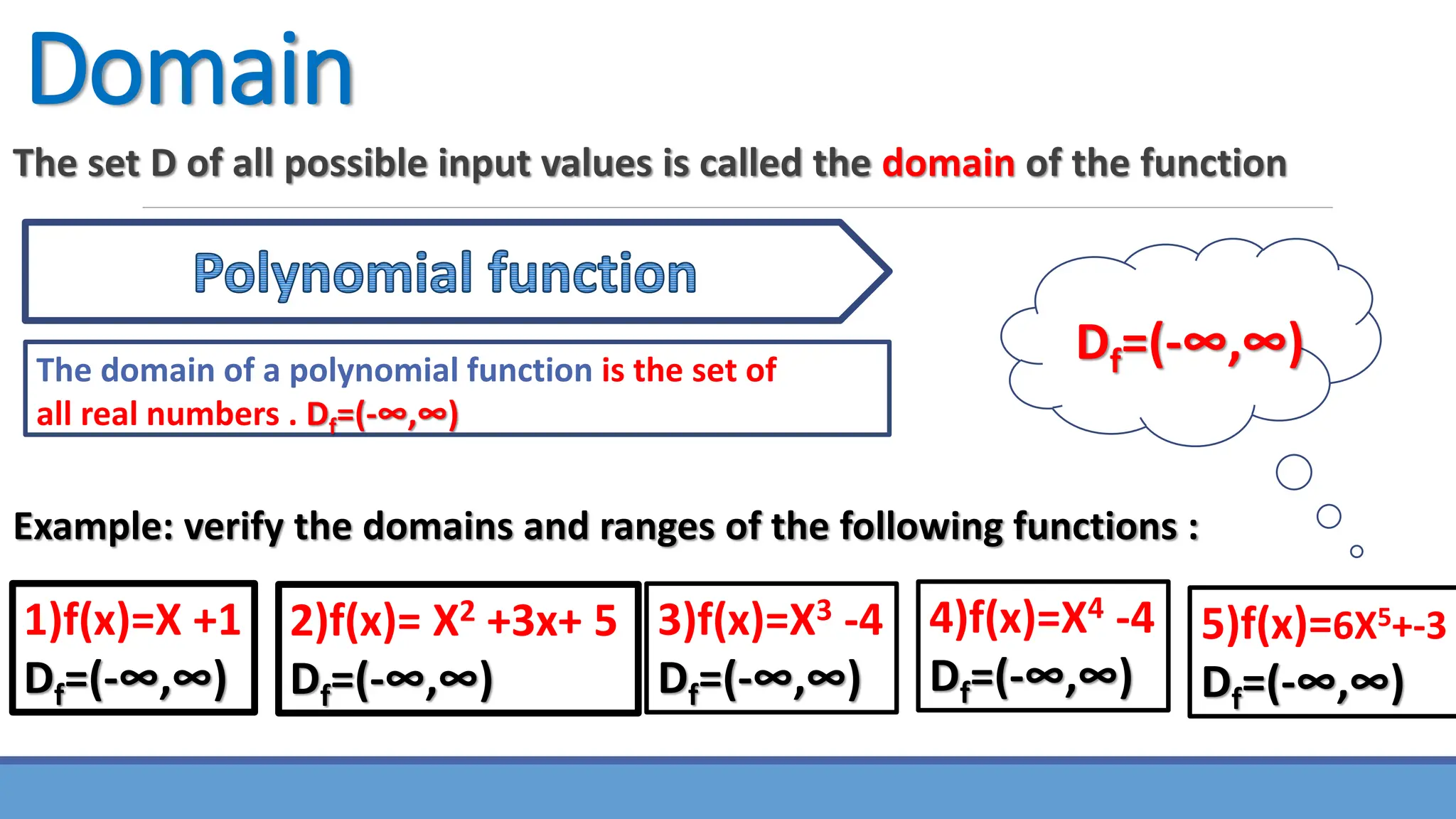
1) The document discusses domains and ranges of functions. It defines domain as the set of all possible input values, and range as the set of all output values. 2) It provides steps to find the domain of rational functions, square root functions, and examples of determining domains and ranges of various functions. 3) Key points covered include: the domain of a polynomial function is all real numbers; finding the domain of a rational function involves setting the denominator equal to zero; the square root function's domain must satisfy the argument being greater than or equal to zero.

1. LECTURE 3
Prepared by:
Assist. Lect. Hiba Abdul –Kareem Assist. Lect. Azam Isam

2. Introduction to function
A function is a relation where every x value has one and only one value of y assigned to it.
The set D of all possible input values is called the domain of the function
The set of all values of f(x) as x varies throughout D is called the range of the function
Domain(input)
Range(output)

6. Domain &Range
For real-valued domains and ranges, the following points
should be satisfied :
1. we cannot divide by zero. The denominator cannot be zero
2. Any value under the square root cannot be negative
Domain
‫قيم‬
x
‫ان‬ ‫دون‬ ‫الدالة‬ ‫في‬ ‫تعويضها‬ ‫يمكن‬ ‫التي‬
‫سالب‬ ‫جذر‬ ‫او‬ ‫صفر‬ ‫مقام‬ ‫الناتج‬ ‫يكون‬
Range
‫قيم‬
y
‫ان‬ ‫دون‬ ‫الدالة‬ ‫في‬ ‫تعويضها‬ ‫يمكن‬ ‫التي‬
‫سالب‬ ‫جذر‬ ‫او‬ ‫صفر‬ ‫مقام‬ ‫الناتج‬ ‫يكون‬

7. Domain
The set D of all possible input values is called the domain of the function
Example: verify the domains and ranges of the following functions :
The domain of a polynomial function is the set of
all real numbers . Df=(-∞,∞)
Df=(-∞,∞)
3)f(x)=X3 -4
Df=(-∞,∞)
1)f(x)=X +1
Df=(-∞,∞)
2)f(x)= X2 +3x+ 5
Df=(-∞,∞)
4)f(x)=X4 -4
Df=(-∞,∞)
5)f(x)=6X5+-3
Df=(-∞,∞)

8. Domain
The set D of all possible input values is called the domain of the function
The domain of a rational function consists of all the real
numbers x, except those for which the denominator is 0
To find the domain for a given rational function
• Set the denominator equal to zero.
• Solve to find the x-values that cause the denominator to equal zero.
• The domain is all real numbers except those found in Step 2.

9. Domain
The set D of all possible input values is called the domain of the function
Example: find the domain for the following rational functions:
𝟏)𝒇 𝒙 =
𝟓𝒙𝟐
𝟑 − 𝒙
3-x=0
X=3
Df ={x∈ R: X≠3}
OR
Df =(-∞, 3 ∪
( (3 , ∞)
-∞ ∞
3

10. Domain
The set D of all possible input values is called the domain of the function
Example: find the domain for the following rational functions:
𝟐)𝒈 𝒙 =
𝒙 − 𝟏
𝒙𝟐 − 𝒙 − 𝟐
𝒙𝟐 − 𝒙 − 𝟐=0
(x-2)(x+1)=0
X=2,x=-1
Dg ={x∈ R: X≠2, : X≠-1}
OR
Dg =(-∞, -1 ∪
( (-1 , 2)∪ (2, ∞)
-∞ ∞
-1 2
c c c

11. Domain
The set D of all possible input values is called the domain of the function
Example: find the domain for the following rational functions:
𝟑)𝑯 𝒙 =
𝟏
𝟑𝑿+𝟐
-
𝟏
−𝟑𝑿−𝟓
3X+2=0
X=-
𝟐
𝟑
-3X-5=0
X=-
𝟓
𝟑
DH ={x∈ R: X≠-
𝟐
𝟑
, : X≠-
𝟓
𝟑
} OR DH =(-∞, -
𝟓
𝟑
∪
( (-
𝟓
𝟑
, -
𝟐
𝟑
)∪ (-
𝟐
𝟑
, ∞)
-∞ ∞
-
𝟓
𝟑
−
𝟐
𝟑
c c c

12. Domain
The set D of all possible input values is called the domain of the function
Example: find the domain for the following rational functions:
𝟒) y=
𝟏
𝒙
X=0
Dy ={x∈ R: X≠0 } OR Dy =(-∞, 0 ∪
( (0 , ∞)
-∞ ∞
𝟎
c c

13. Domain
The set D of all possible input values is called the domain of the function
The square root of a negative number is NOT a real number. i.e., the square
root function cannot accept negative numbers as inputs
Finding the Domain of a Square Root Function
Step 1: Set everything underneath the square root greater than or equal to 0.
Step 2: Solve the inequality from step 1.
Step 3: Write the result from step 2 in interval notation

14. Domain
Example: verify the domains and ranges of the following functions:
1)f(x)= 𝒙 − 𝟏𝟐
X-12≥0
x≥12
Df=[12, ∞)
2)f(x)=3 𝒙 − 𝟓
X-5≥0
x≥5
Df=[5, ∞)
The set D of all possible input values is called the domain of the function

15. Domain
3)f(x)= 𝟐𝒙 − 𝟕
2X-7≥0
2x≥7
x≥
𝟕
𝟐
Df=[
𝟕
𝟐
, ∞)
4)f(x)= −𝒙 − 𝟑
-X-3≥0
-x≥3
x≤-3
Df (-∞,-3]

16. Domain
5)f(x)=
𝟑
𝟐𝒙−𝟑
2X-3>0
2x>3
x>
𝟑
𝟐
Df=(
𝟑
𝟐
, ∞)
6)f(x)= 𝒙𝟐 − 𝟑
𝒙𝟐
-3≥0
𝒙𝟐
≥3
x ≥ ± 𝟑
Df =[- 𝟑, 𝟑]

17. Domain
5)f(x)=
𝒙−𝟏
𝒙+𝟐
X-1 ≥0
x ≥ 1
x+2>0
x>-2
Df = { x: x ≥ 1} ∩{ x: x x>-2}
Df=[𝟏, ∞)
𝟏
c
−𝟐
c

18. Range
The set of all values of f(x) as x varies throughout D is called the range of the function
‫اس‬ ‫اعلى‬
‫فردي‬
Rf=(-∞, ∞)
‫زوجي‬ ‫اس‬ ‫اعلى‬
Rf=[‫عدد‬, ∞)
‫او‬
Rf=(-∞, ‫]عدد‬
1)f(x)=X3 -8
Rf=(-∞, ∞)
2)f(x)=X2 +5
y= X2 +5
X2 =y-5
X= 𝒚 − 𝟓
y-5≥0
Y ≥5
Rf =[5, ∞)
3)f(x)=X -1
Rf=(-∞, ∞)

19. Range
The set of all values of f(x) as x varies throughout D is called the range of the function
‫اس‬ ‫اعلى‬
‫فردي‬
Rf=(-∞, ∞)
‫زوجي‬ ‫اس‬ ‫اعلى‬
Rf=[‫عدد‬, ∞)
‫او‬
Rf=(-∞, ‫]عدد‬
4)H(x)=X2
y=X2
X= 𝒚
y ≥0
RH =[0, ∞)
5)f(x)=4-X2
y= 4-X2
X2 =4-y
X=± 𝟒 − 𝒚
4-y≥0
-y ≥-4
y≤4 , Rf=(-∞,4]

20. Range
The set of all values of f(x) as x varies throughout D is called the range of the function
‫كل‬
‫القيم‬ ‫عدا‬ ‫ما‬ ‫الحقيقة‬ ‫االعداد‬
‫التي‬
‫صفر‬ ‫يساوي‬ ‫المقام‬ ‫تجعل‬
Rf =(-∞, ∪
(
‫عدد‬ ( ‫عدد‬, ∞)
(
‫نجعل‬
x
‫بداللة‬
y
‫لجعل‬ ‫طريقة‬ ‫وايجاد‬
y
‫المقام‬ ‫في‬
‫بالصفر‬ ‫مساواتها‬ ‫ثم‬
)
Rf =R/{ ‫}العدد‬
1)y=1/x
y=1/x
X=1/y
Y=0
Rf =(-∞, 0 ∪
( (0 , ∞)
2)y=x+1/x-2
y=x+1/x-2
xy-2y=x+1
xy-x=1+2y
x(y-1)=1+2y
x=1+2y/y-1
y-1=0
y=1
Rf =(-∞, 1 ∪
( (1 , ∞)

21. Range
1)y=
𝟏
𝟒−𝒙𝟐
𝒚𝟐
=
𝟏
𝟒−𝒙𝟐
4𝒚𝟐
-𝒚𝟐
𝒙𝟐
=1
𝒚𝟐
𝒙𝟐
=4𝒚𝟐
-1
𝒙𝟐
=4𝒚𝟐
-1/𝒚𝟐
X=
4𝒚𝟐−1
𝒚
4𝒚𝟐
−1 ≥0
4𝒚𝟐
≥1
𝒚𝟐
≥
𝟏
𝟒
𝒚 ≥ ±
𝟏
𝟐
y=0
R= {y ∈ R: y≠0 }∩ {y ∈ R: 𝒚 ≥ ±
𝟏
𝟐
}

22. Homework
For each function, identify the domain

23. Homework
For each function, identify the domain
1)
2)

24. Identify the domain and range 𝒚 =
𝟏
𝒙+𝟏
-
𝟏
𝒙−𝟏
Homework

25. Homework