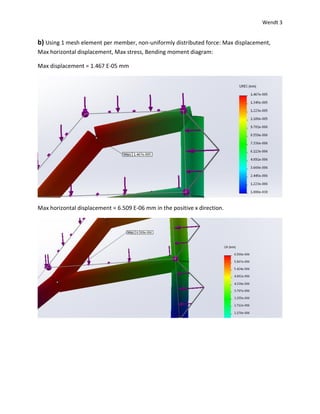
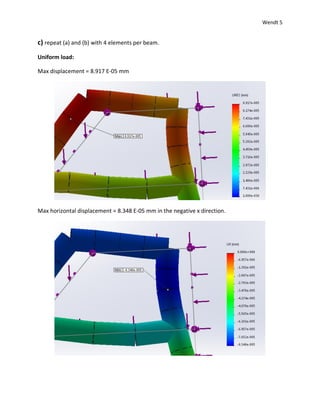
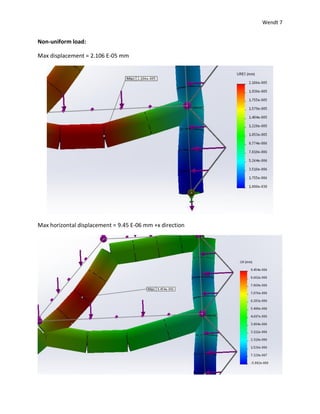
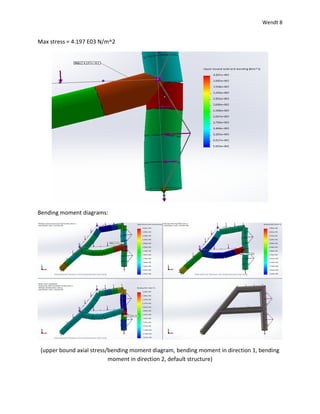
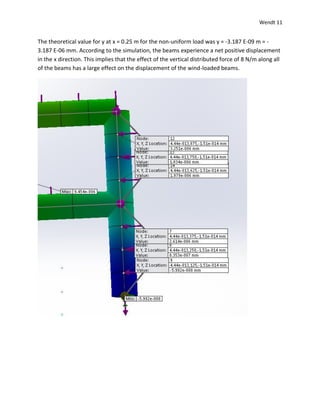
1) The document reports on a beam analysis simulation where beams were subjected to uniform and non-uniform loads. 2) Maximum displacements, stresses, and bending moments were reported from the simulation for different mesh element sizes. 3) Beam differential equations were derived for uniform and non-uniform loads and solved to find theoretical deflections. 4) The theoretical deflections did not match the simulation results, likely due to additional loading conditions and deflection absorption in the simulation that were not accounted for in the simplified theoretical model.

1. Wendt 1
Nathan Wendt
ME 313
Section 3
Lab 12
Beam Analysis
a) Using 1 mesh element per member, uniformly distributed force: Max displacement,
Max horizontal displacement, Max stress, Bending moment diagram:
The max displacement occurred at the upper left corner of the structure at 8.88E-05 mm.
The max horizontal displacement occurred at the top right junction at 7.593 E-05 mm in the
negative x direction.

2. Wendt 2
Max stress occurred on the bottom right beam at 1.703E04 N/m^2
(Bending moment diagrams for upper bound axial and ending, bending in direction 1, bending
in direction 2, and the basic structure.)

3. Wendt 3
b) Using 1 mesh element per member, non-uniformly distributed force: Max displacement,
Max horizontal displacement, Max stress, Bending moment diagram:
Max displacement = 1.467 E-05 mm
Max horizontal displacement = 6.509 E-06 mm in the positive x direction.

4. Wendt 4
Max stress = 4.197 E03 N/m^2
Bending moment diagram:
(upper bound axial stress/bending moment diagram, bending moment in direction 1, bending
moment in direction 2, default structure)

5. Wendt 5
c) repeat (a) and (b) with 4 elements per beam.
Uniform load:
Max displacement = 8.917 E-05 mm
Max horizontal displacement = 8.348 E-05 mm in the negative x direction.

6. Wendt 6
Mas stress = 1.703 E04 N/m^2
Bending moment diagram:
(Bending moment diagrams for upper bound axial and ending, bending in direction 1, bending
in direction 2, and the basic structure.)

7. Wendt 7
Non-uniform load:
Max displacement = 2.106 E-05 mm
Max horizontal displacement = 9.45 E-06 mm +x direction

8. Wendt 8
Max stress = 4.197 E03 N/m^2
Bending moment diagrams:
(upper bound axial stress/bending moment diagram, bending moment in direction 1, bending
moment in direction 2, default structure)

9. Wendt 9
d) Beam differential equations
Uniform:
𝐸𝐼
𝑑2
𝑦
𝑑𝑥2
= 𝑀 = −
1
2
𝑤𝑥2
+
1
2
𝑤𝐿𝑥
Where:
𝑤 = 25 𝑁/𝑚, L = 0.5 m
Integrating twice yields:
𝐸𝐼𝑦 = −
25
24
𝑥4
+
25
24
𝑥3
+ 𝐶1 𝑥 + 𝐶2
Because y = 0 at both ends and x = 0 at the bottom end we can see that C2 = 0. At the top end, y
= 0, x = 0.5 yields:
0 = −0.0651 + 0.1302 + 0.5𝐶1
𝐶1 = −0.1302
So,
𝑦 = −
25
24𝐸𝐼
𝑥4
+
25
24𝐸𝐼
𝑥3
−
0.1302
𝐸𝐼
𝑥
Non-uniform:
𝐸𝐼
𝑑2
𝑦
𝑑𝑥2
= 𝑀 =
1
4
𝑤0 𝐿𝑥 −
𝑤0
3𝐿
𝑥3
+
2𝑤0
3𝐿
〈𝑥 −
1
2
𝐿〉3
Integrating twice yields:
𝐸𝐼𝑦 =
1
24
𝑤0 𝐿𝑥3
−
𝑤0
60𝐿
𝑥5
+
𝑤0
30𝐿
〈𝑥 −
1
2
𝐿〉5
+ 𝐶1 𝑥 + 𝐶2
𝑤0 = 25 𝑁, L = 0.5 m
Solving at x = 0, y = 0 yields: C2 = 1.627 E-03
Solving at x = L, y = 0 yields: C1 = -84.634 E-03
𝑦 =
25
48𝐸𝐼
𝑥3
−
25
30𝐸𝐼
𝑥5
+
25
15𝐸𝐼
〈𝑥 − 0.25〉5
−
(84.63 ∗ 10−3
)
𝐸𝐼
𝑥 +
1.63 ∗ 10−3
𝐸𝐼

10. Wendt 10
e) In the previous equations E = 2.1 * 10^11 and I = π(0.14^4 – 0.06^4)/64 = 18.221 * 10 ^-6
according to the derived equation for the uniformly loaded side beams the deflection at the
point x = L/2 = 0.25 m should be y = -5.32 E-09 m = -5.32 E-06 mm whereas the deflections
given by the simulation are -8.348 E-05 for the top beam and -3.031 E-05 for the bottom beam.
The theoretical value is approximately 1/10th
the average of these values. This is likely due to
the additional loading conditions on the beams (namely the weight) as well as the deflection
absorbed by the other beams.

11. Wendt 11
The theoretical value for y at x = 0.25 m for the non-uniform load was y = -3.187 E-09 m = -
3.187 E-06 mm. According to the simulation, the beams experience a net positive displacement
in the x direction. This implies that the effect of the vertical distributed force of 8 N/m along all
of the beams has a large effect on the displacement of the wind-loaded beams.