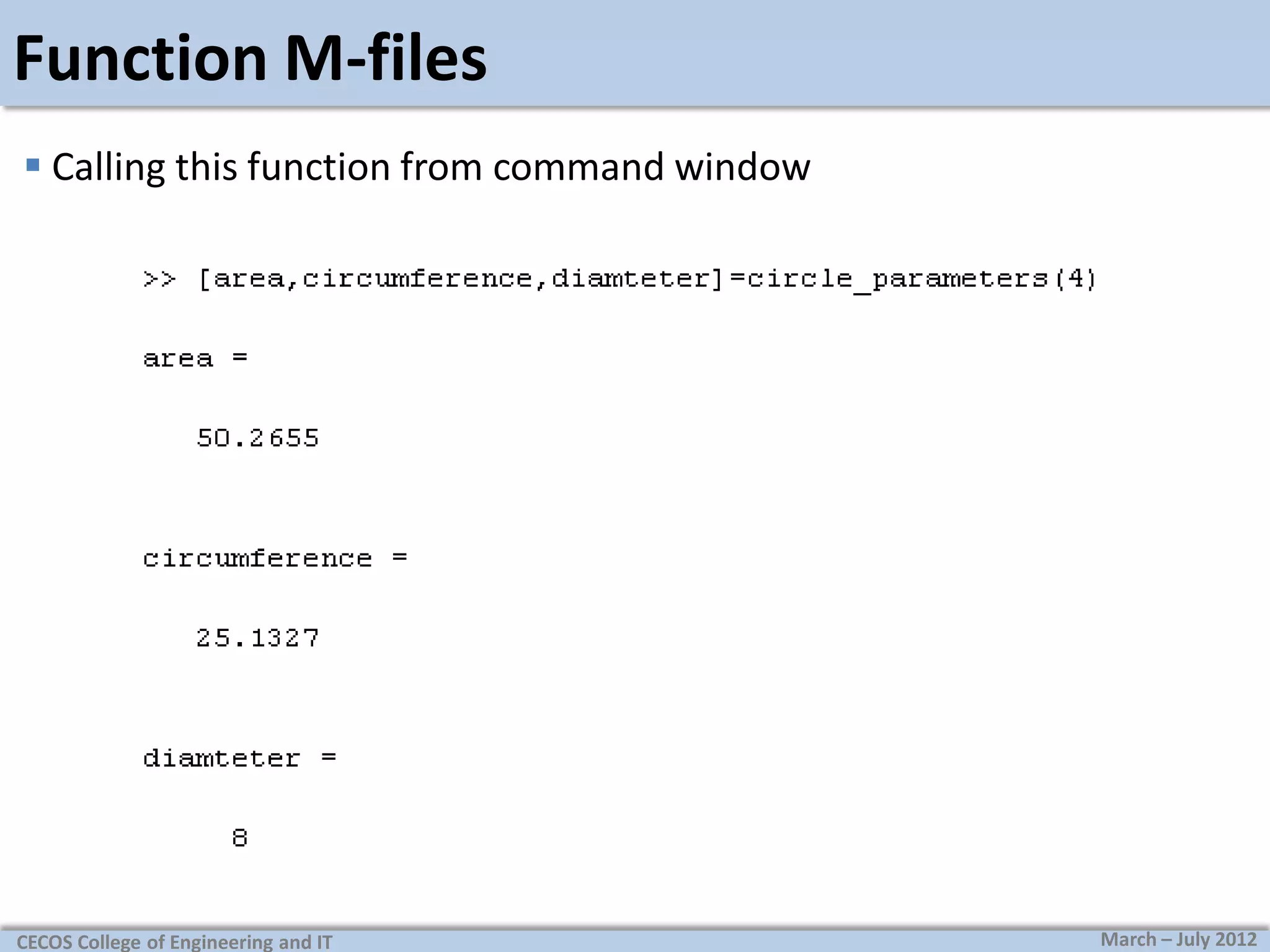
This document discusses matrices and matrix operations in MATLAB. It begins by defining what a matrix is and how they are represented in MATLAB. It then covers topics like defining matrices, accessing matrix elements, built-in matrix functions like diag, eye, and size, and matrix operations like addition, multiplication, and dot notation. The document ends by discussing M-files in MATLAB, including how to create script and function M-files, use comments, and provide examples.

1. Lab No.02
M-files and Matrix operations
Designed by : Dawar Awan
dawar@cecos.edu.pk
CECOS College of Engineering and IT
March – July 2012

2. Matrices
 MATLAB treats every thing as a matrix (check the Workspace)
 1-by-1 matrices are interpreted as scalars
 Matrices with only one row or one column are known as vectors
 A matrix is a rectangular array of numbers.
1 9 2 6
7 8 3 5
1 8 2 4
A matrix with 3 rows, 4 columns, and 12 elements
CECOS College of Engineering and IT
March – July 2012

3. Defining matrices
>> A = [1 2 3; 4 5 6; 7 8 9];
>> A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
and
>> A = [ 1 2 3
456
7 8 9 ];
Defines
A=
1
3
4
5
6
7
CECOS College of Engineering and IT
2
8
9
March – July 2012

4. Accessing matrix elements
 The matrix element located in the i-th row and j-th column of
“A” is referred to as, A(i,j)
 Try the following instruction and observe the change in “A”
>> A(2,3) = 10
CECOS College of Engineering and IT
March – July 2012

5. Some Built-in matrix functions
Function Description
diag
eye
magic
ones
rand
triu
tril
zeros
size
length
find
:
:
:
:
:
:
:
:
:
:
:
CECOS College of Engineering and IT
returns diagonal elements as vector
identity matrix
magic square
matrix of ones
randomly generated matrix
upper triangular part of a matrix
lower triangular part of a matrix
matrix of zeros
Number of rows and columns in a matrix
Length of an array
find indices of some elements in array
March – July 2012

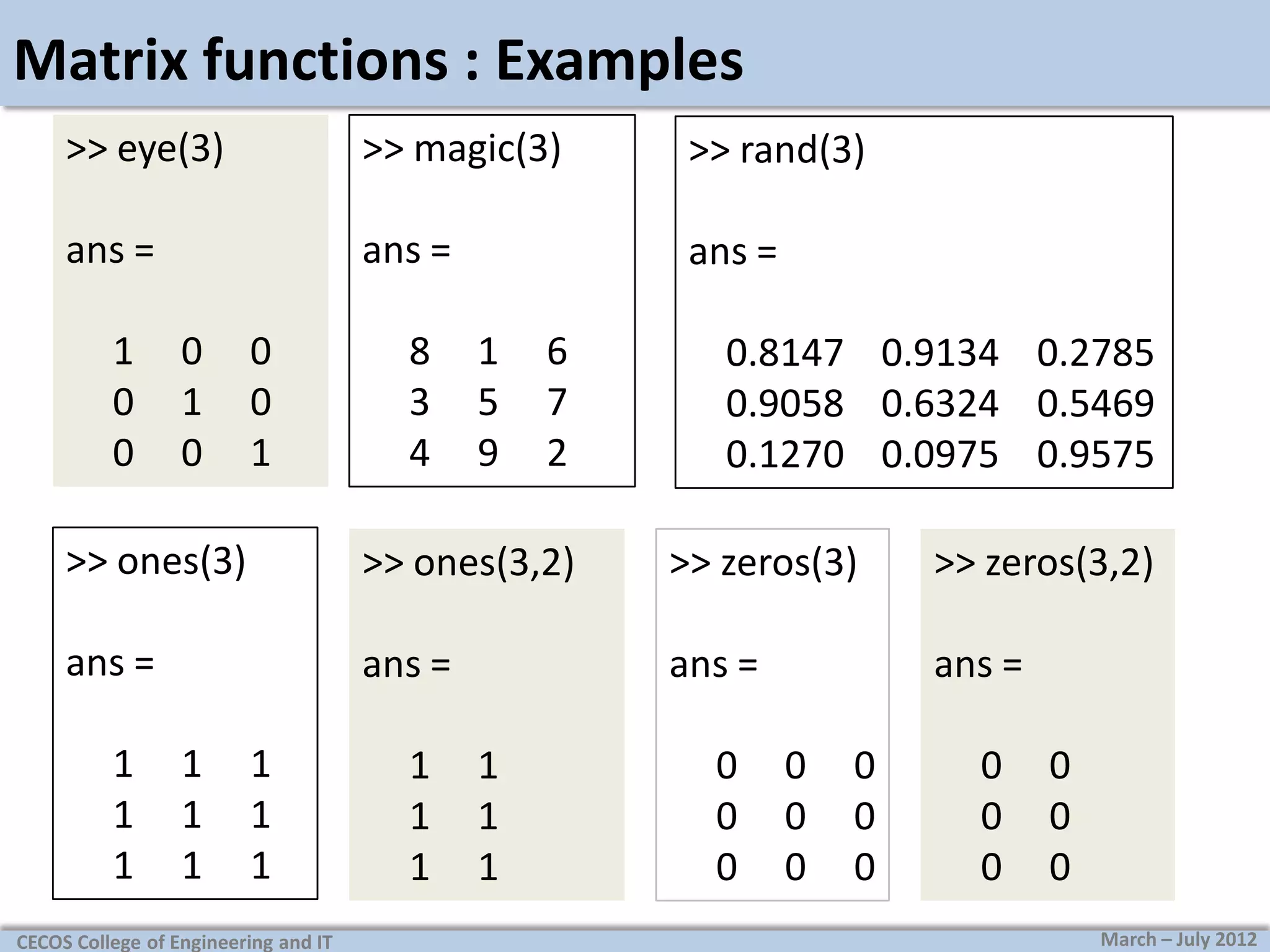
6. Matrix functions : Examples
>> a=[1 2 3;4 5 6;7 8 9]
a=
1
4
7
2
5
8
3
6
9
>> diag(a)
>> triu(a)
>> tril(a)
>> size(a)
>> length(a)
ans =
ans =
ans =
ans =
ans =
1
5
9
CECOS College of Engineering and IT
1
0
0
2
5
0
3
6
9
1
4
7
0
5
8
0
0
9
3
3
3
March – July 2012

7. Matrix functions : Examples
>> eye(3)
>> magic(3)
>> rand(3)
ans =
ans =
ans =
1
0
0
0
1
0
0
0
1
8
3
4
1
5
9
6
7
2
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
>> ones(3)
>> ones(3,2)
>> zeros(3)
>> zeros(3,2)
ans =
ans =
ans =
ans =
1
1
1
1
1
1
1
1
1
CECOS College of Engineering and IT
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
March – July 2012

8. Matrix functions : Examples
>> rand(3,2)
ans =
0.9649 0.9572
0.1576 0.4854
0.9706 0.8003
CECOS College of Engineering and IT
March – July 2012

9. Matrix operations
+
*
^
'
/
=>
=>
=>
=>
=>
=>
Addition
Subtraction
Multiplication
Power
Conjugate transpose
Division
 To perform index by index operation, use dot (.)
notation
./
.*
.^
.'
=>
=>
=>
=>
CECOS College of Engineering and IT
Index by index division
Index by index multiplication
Index by index power
Non conjugate transpose
March – July 2012

10. Dot notation
 Observe the change in result due to the “dot”
CECOS College of Engineering and IT
March – July 2012

11. Examples/Exercise
1
4
7
C=
B=
A=
2
5
8
3
6
9
1
2
3
1
2
3
1
2
3
1
D=
2
1
2
2
1
2
1
 Practice the following matrix operations
A+B, A’, A*B, 2*A, A/2, A/B, A./B, C/D, C./D, C*D, C.*D, C^2, C.^2
CECOS College of Engineering and IT
March – July 2012

12. Colon notation
CECOS College of Engineering and IT
March – July 2012

13. M - files
 M-files are script/text files containing MATLAB commands
Script M-file
Function M-file
 To make a script M-file, you need to open a file using the built-in
MATLAB editor.
 There are two ways to accomplish it:
1. From file menu, click NEW
2. Type edit on command line
CECOS College of Engineering and IT
March – July 2012

14. M - files
 To save the M-file go to the “file” menu and click on “save”.
 The name should not contain spaces, should not start with a number and should not
be same as any built-in function.
 The extension of this file should be “.m”
CECOS College of Engineering and IT
March – July 2012

15. M - files
 This code can now be executed in two ways
1. Write the name of file on command window
(excluding “.m”)
2. Under the “debug” menu, click “Run”
 The variables used in the M-file will be maintained in the workspace
and hence accessible from the command window.
CECOS College of Engineering and IT
March – July 2012

16. M - files
 Code written in M-file to calculate various parameters of a circle
 Check the values of the variables after running the M-file
CECOS College of Engineering and IT
March – July 2012

17. Comments
 While writing any code, it’s a good practice to write proper comments
against each instruction.
 In MATLAB, any thing written after “%” is treated as a comment and is
ignored by the compiler.
CECOS College of Engineering and IT
March – July 2012

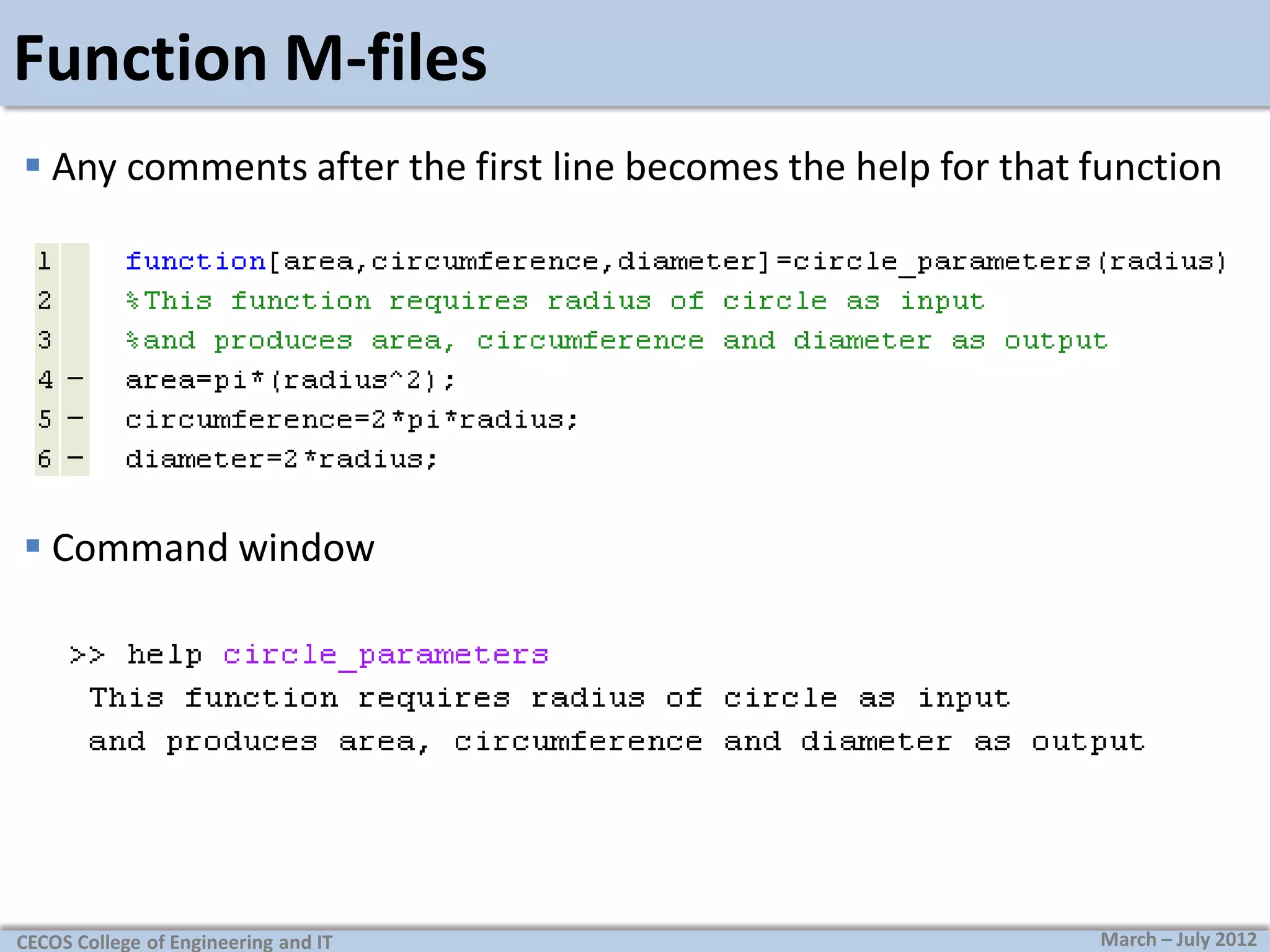
18. Function M-files
 User defined functions
 These M-files start with a keyword, “function”
 The first line of these files should look like
function[output variables]=functionName(input variables)
 These files are saved with the funtionName.m as file name.
 An example:
CECOS College of Engineering and IT
March – July 2012

19. Function M-files
 Calling this function from command window
CECOS College of Engineering and IT
March – July 2012

20. Function M-files
 Any comments after the first line becomes the help for that function
 Command window
CECOS College of Engineering and IT
March – July 2012

21. Tasks
1- Generate a vector of 50 elements having random values between 0
and 50.
2- Generate a vector, containing all the odd numbers between 0 and
100.
3- Create a function M-file that accepts two numbers and generates
there sum, product and difference as output.
4- Use Cramer's rule to solve the following set of equations.
3x1 - 1x2 + 0x3 = 1
1x1 + 4x2 - 2x3 = 5
0x1 - 2x2 + 8x3 = 6
CECOS College of Engineering and IT
March – July 2012