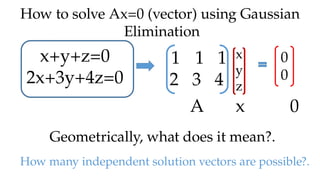
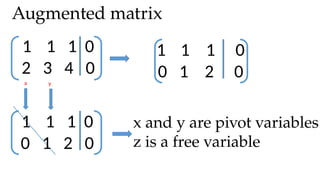
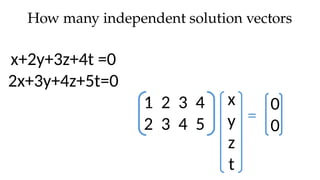
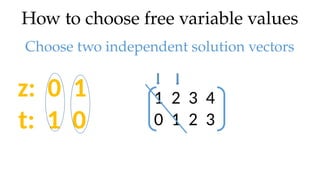
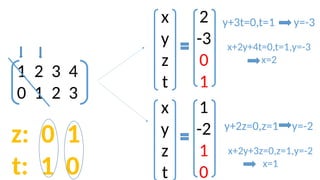
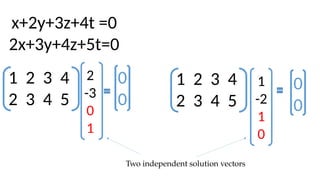
The document discusses Gaussian elimination for solving systems of linear equations, highlighting its foundational concepts such as linear combinations and vector spaces. It outlines the process of using reduced row echelon form (RREF) to determine basis sets for row and column spaces and explains the geometrical interpretation of solution vectors in homogeneous systems. Additionally, it explores determining the number of independent solution vectors based on free variables and provides examples to illustrate these concepts.

1. Gauss and Gaussian Elimination
for solving system of linear equations

2. Gaussian Elimination process though simple enough that can be
taught to even a 7th
standard student, hides lots of interesting
properties.
To unravel the Gaussian process, you need
concepts of linear combination, Linear
independence and vector space In Linear Algebra

3. https://www.youtube.com/watch?v=2j5Ic2V7wq4
Algebra 53 - Elementary Row Operations – YouTube
https://www.youtube.com/watch?v=2GKESu5atVQ
Gaussian Elimination Videos

9. Pivotal column location depends on Column-
independence with columns in the left of it
1 2 1 2
2 4 3 4
3 6 6 8
A=
Second column is multiple of first
Third column is LC of first two
1 2 3 3
2 4 6 3
3 5 8 1
A= rref(A)=
1 0 1 0
0 1 1 0
0 0 0 1
1 2 0 0
0 0 1 0
0 0 0 1
rref(A)=

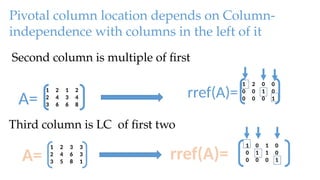
10. How to use rref to get basis set for row space and
column space.
Ans:
all nonzero rows of rref(A) form basis set for row space
[a b]=rref(A)
a=reduced matrix
b=array giving index of pivotal columns
Brows=a(1:length(b),:) % Row-space basis set
Bcols=A(:,b) % column-space basis set from columns of A
Note: multiple ways to choose a basis set.

11. Homogeneous system of
equations
Ax=0
,
1 vector
0 vecor is m 1
If A is m n
x is n




12. How to solve Ax=0 (vector) using Gaussian
Elimination
Geometrically, what does it mean?.
How many independent solution vectors are possible?.
x+y+z=0
2x+3y+4z=0
1 1 1
2 3 4
x
y
z
0
0
A x 0

13. 1 1 1 0
2 3 4 0
1 1 1 0
0 1 2 0
1 1 1 0
0 1 2 0
x and y are pivot variables
z is a free variable
Augmented matrix
x y

14. 1 1 1 0
0 1 2 0
x and y are pivot variables
z is a free variable
Choose a non-zero value for the free variable z and do backward substitution
z=1
Solve the last equation y+2z=0
y=-2
Solve the first equation x+y+z=0
x=1
x
y
z
1
-2
1

15. 1 1 1
2 3 4
1
-2
1
0
0

16. Generalization:
How many independent solution vectors?
Answer: Equal to Number of free variables

17. x+2y+3z+4t =0
2x+3y+4z+5t=0
How many independent solution vectors
x
y
z
t
1 2 3 4
2 3 4 5
0
0
=

18. On Gaussian elimination
x+2y+3z+4t =0
2x+3y+4z+5t=0
1 2 3 4
0 -1 -2 -3
x and y are pivot variables
z and t are free variables
Two independent solution vectors!
1 2 3 4
0 1 2 3
Augmentation omitted
x y z t

19. How to choose free variable values
Choose two independent solution vectors
z: 0 1
t: 1 0
1 2 3 4
0 1 2 3

20. 1 2 3 4
0 1 2 3
x
y
z
t
2
-3
0
1
x
y
z
t
1
-2
1
0
z: 0 1
t: 1 0
y+3t=0,t=1 y=-3
x+2y+4t=0,t=1,y=-3
x=2
y+2z=0,z=1 y=-2
x+2y+3z=0,z=1,y=-2
x=1

21. 1 2 3 4
2 3 4 5
x+2y+3z+4t =0
2x+3y+4z+5t=0
2
-3
0
1
0
0
1 2 3 4
2 3 4 5
1
-2
1
0
0
0
Two independent solution vectors

22. Any linear combination of the obtained Solution
vectors is solution to the original problem
That is, solution space is a vector space
x
y
z
t
1 2 3 4
2 3 4 5
0
0
=
2
-3
0
1
1
-2
1
0
x
y
z
t
=C1 C2

23. If b is expressible as LC
of those columns,
then solution exist
In Ax=b

25. Example

26. Example

27. Example