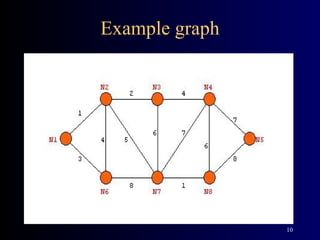
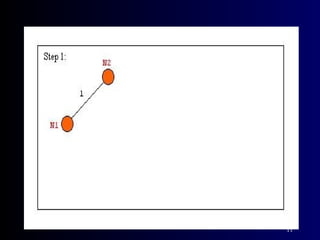
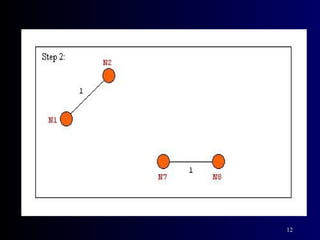
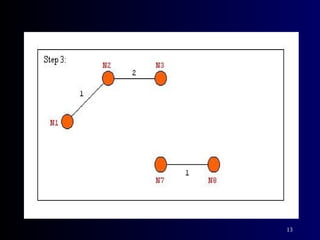
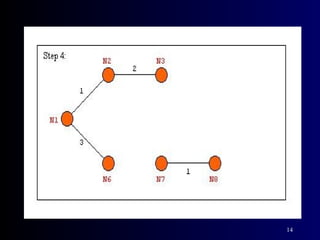
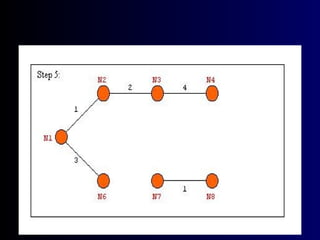
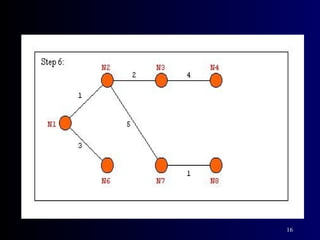
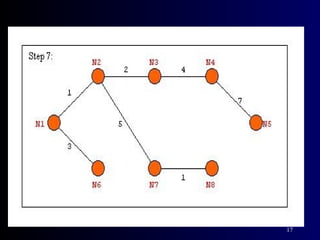
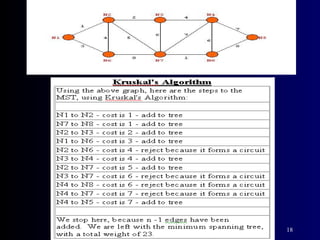
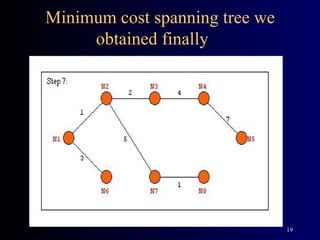
The document summarizes Kruskal's algorithm for finding a minimum cost spanning tree in a graph. Kruskal's algorithm works by sorting the edges by cost and building the spanning tree by adding edges in order of increasing cost, skipping edges that would create cycles. An example graph is provided and the minimum cost spanning tree obtained using Kruskal's algorithm on that graph is shown.

1. KUVEMPU UNIVERSITY Department of Computer Science Jnana Sahyadri Shankarghatta Seminar on “ Kruskal’s Algorithm ” Presented by, Chaitra.M.S 3 rd sem , M.Sc, Dept. Of Computer Science, Shankarghatta. Under the guidance of, Suresh.M, Dept. Of Computer Science, Shankarghatta.

2. Contents Spanning trees Finding a spanning tree Minimum-cost spanning trees Kruskal’s algorithm And example

3. Spanning Trees

4. Spanning trees Suppose you have a connected undirected graph Connected: every node is reachable from every other node Undirected: edges do not have an associated direction ...then a spanning tree of the graph is a connected subgraph in which there are no cycles A connected, undirected graph Four of the spanning trees of the graph

5. Finding a spanning tree To find a spanning tree of a graph, pick an initial node and call it part of the spanning tree do a search from the initial node: each time you find a node that is not in the spanning tree, add to the spanning tree both the new node and the edge you followed to get to it An undirected graph

6. Minimizing costs Suppose you want to supply a set of houses (say, in a new subdivision) with: electric power water sewage lines telephone lines To keep costs down, you could connect these houses with a spanning tree (of, for example, power lines) However, the houses are not all equal distances apart To reduce costs even further, you could connect the houses with a minimum-cost spanning tree

7. Minimum-cost spanning trees Suppose you have a connected undirected graph with a weight (or cost ) associated with each edge The cost of a spanning tree would be the sum of the costs of its edges A minimum-cost spanning tree is a spanning tree that has the lowest cost A B E D F C 16 19 21 11 33 14 18 10 6 5 A connected, undirected graph A B E D F C 16 11 18 6 5 A minimum-cost spanning tree A B E D F C 16 19 21 11 33 14 18 10 6 5 A connected, undirected graph

8. Kruskal algorithm(E,cost,n,t) //E is set of edges in G .G has n vertices.Cost[u,v] is //cost of edge(u,v).t is the set of edges in minimum-cost //spanning tree.the final cost is returned. { //construct a heap out of the edge costs using heapify For i=:1 to n do parent[i]:=-1; //each vertex is in a different set. i:=0;mincost:=0.0; While((i<n-1) and (heap not empty)) do { //delete a minimum cost edje(u,v) from the heap and reheapify using Adjust; j:=Find(u); k:=Find(v);

9. If (j!=k) then { i:=i+1; t[i,1]:=u; t[i,2]:=v; mincost:=mincost+cost[u,v]; union(j,k); } } if(i!=n-1) then write(“no spanning tree”); else return mincost; }

10. Example graph

19. Minimum cost spanning tree we obtained finally

20. Any queries???????????

21. Thank U………………