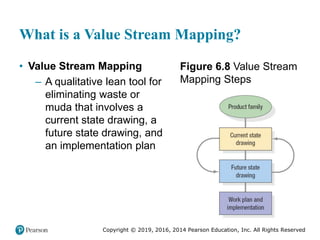
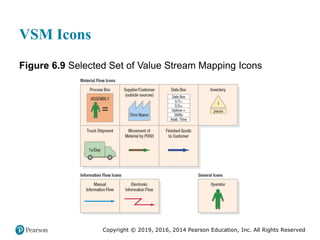
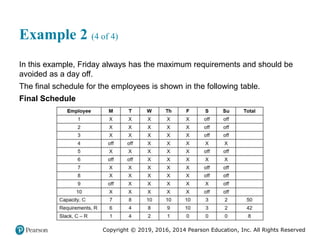
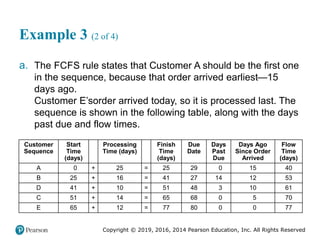
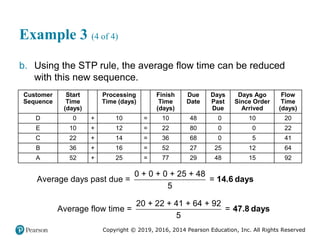
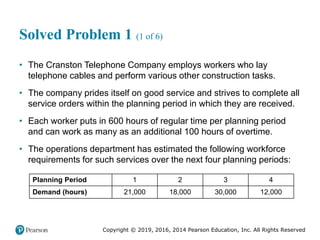
This document provides an overview of operations management and supply chain management concepts from the textbook "Operations Management: Processes and Supply Chains". It defines key terms like operations, processes, competitive priorities and capabilities. It also describes the role of operations in an organization and how corporate strategy, market analysis and operations strategy are connected. Finally, it identifies nine competitive priorities used in operations strategy and discusses how firms can develop capabilities in cost, quality, time and flexibility.







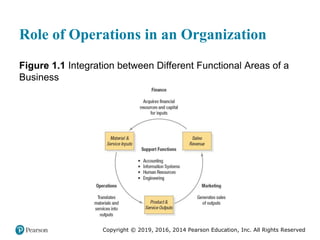
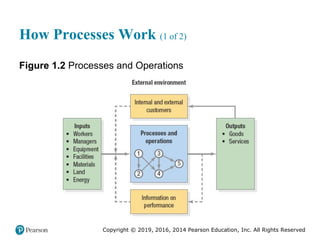
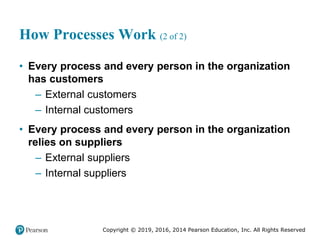


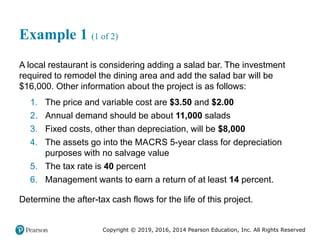
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
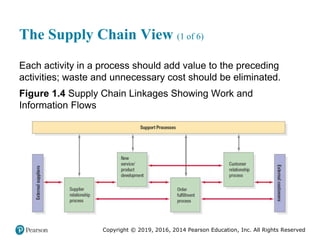
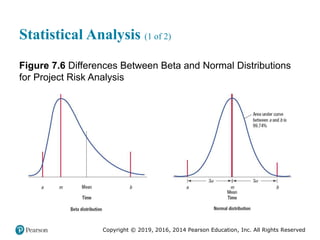
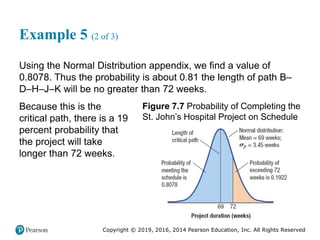
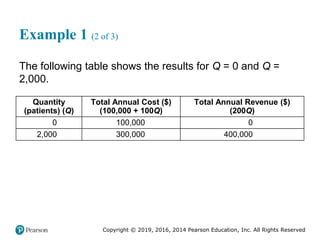
The Supply Chain View (2 of 6)
Supplier relationship process – A process that selects the
suppliers of services, materials, and information and facilitates
the timely and efficient flow of these items into the firm
Figure 1.4 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-15-320.jpg)
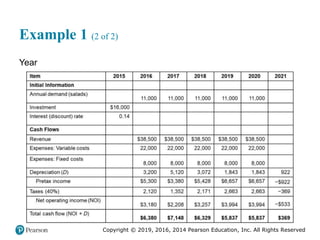
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Supply Chain View (3 of 6)
New service/product development – A process that designs and
develops new services or products from inputs received from
external customer specifications or from the market in general
through the customer relationship process
Figure 1.4 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-16-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Supply Chain View (4 of 6)
Order fulfillment process – A process that includes the activities
required to produce and deliver the service or product to the
external customer
Figure 1.4 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-17-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Supply Chain View (5 of 6)
Customer relationship process – A process that identifies,
attracts and builds relationships with external customers and
facilitates the placement of orders by customers (customer
relationship management)
Figure 1.4 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-18-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Supply Chain View (6 of 6)
Support Processes - Processes like Accounting, Finance,
Human Resources, Management Information Systems and
Marketing that provide vital resources and inputs to the core
processes
Figure 1.4 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-19-320.jpg)





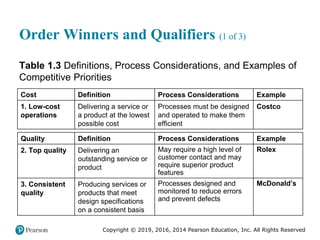
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Order Winners and Qualifiers (2 of 3)
Table 1.3 [continued]
Time Definition Process Considerations Example
4. Delivery speed Quickly filling a
customer’s order
Design processes to reduce
lead time
Netflix
5. On-time delivery Meeting delivery-time
promises
Planning processes used to
increase percent of customer
orders shipped when
promised
United
Parcel
Service
(UPS)
6. Development
speed
Quickly introducing a
new service or a
product
Process involve cross-
functional integration and
involvement of critical
external suppliers
Zara](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-28-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Order Winners and Qualifiers (3 of 3)
Table 1.3 [continued]
Flexibility Definition Process Considerations Example
7. Customization Satisfying the unique
needs of each
customer by
changing service or
product designs
Processes typically have
low volume, close customer
contact, and can be easily
reconfigured to meet
unique customer needs
Ritz Carlton
8. Variety Handling a wide
assortment of
services or products
efficiently
Processes are capable of
larger volumes than
processes supporting
customization
Amazon.com
9. Volume
flexibility
Accelerating or
decelerating the rate
of production of
services or products
quickly to handle
large fluctuations in
demand
Processes must be
designed for excess
capacity and excess
inventory
The United
States Postal
Service (USPS)](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-29-320.jpg)








































![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Process Charts (3 of 6)
Figure 2.10 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-83-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Process Charts (4 of 6)
Figure 2.10 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-84-320.jpg)








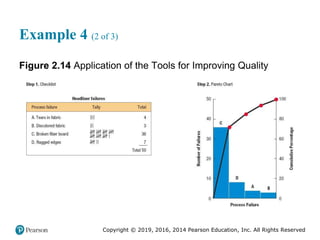
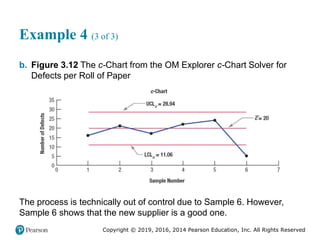
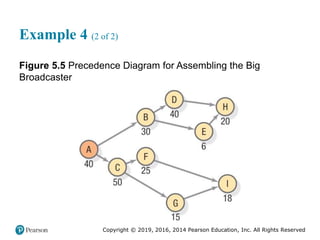
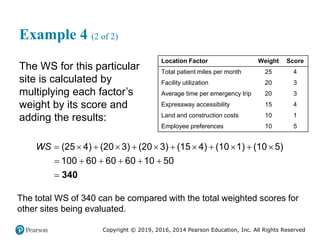
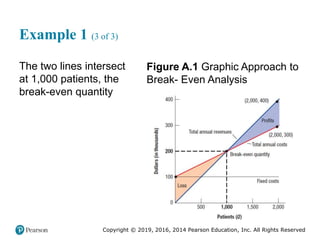
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
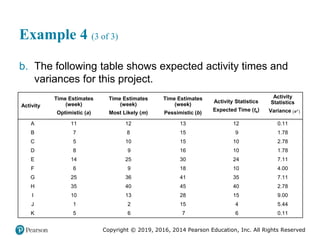
Example 4 (3 of 3)
Figure 2.14 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-97-320.jpg)





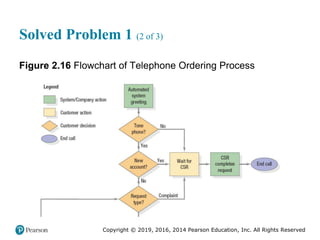
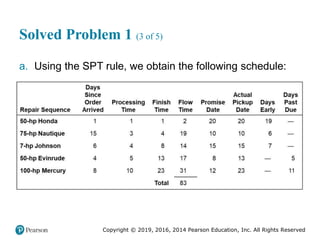
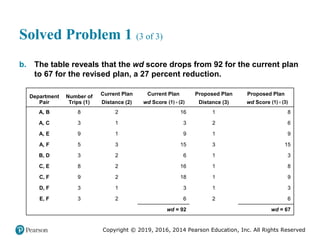
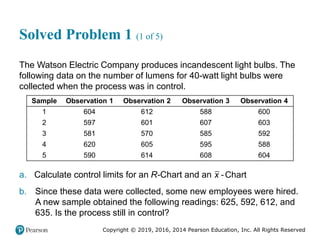
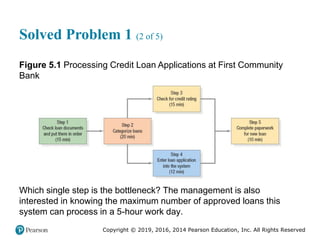
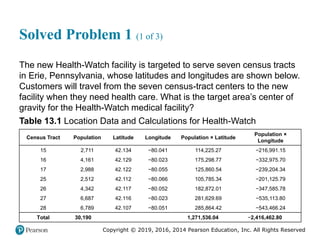
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
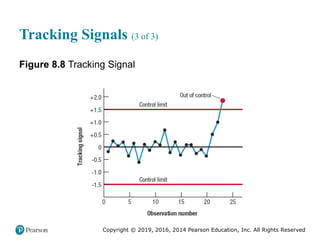
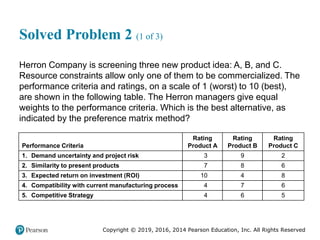
Solved Problem 1 (3 of 3)
Figure 2.16 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-104-320.jpg)


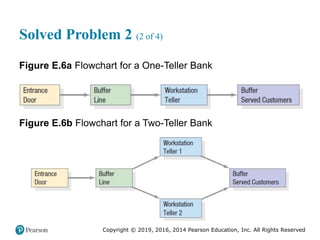
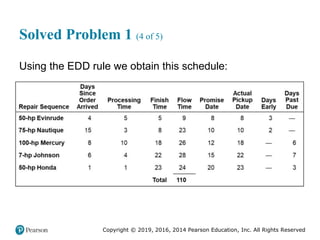
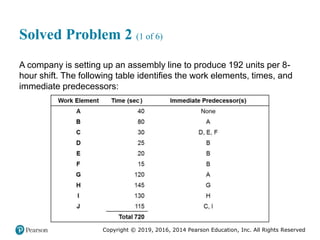
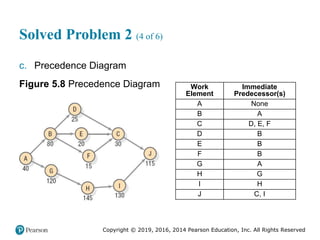
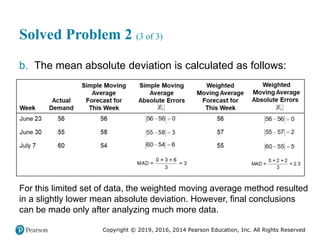
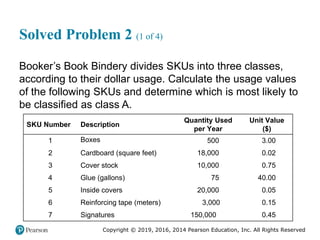
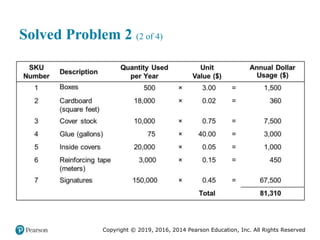
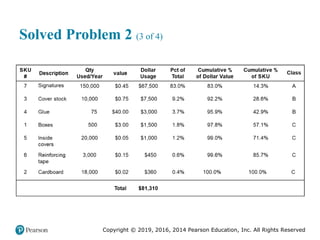
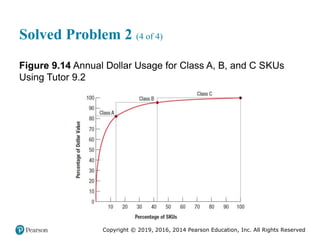
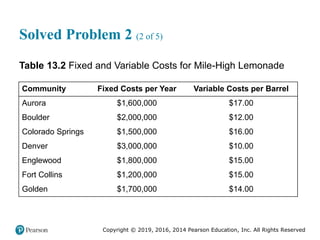
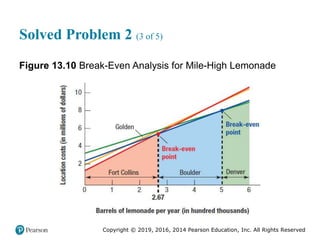
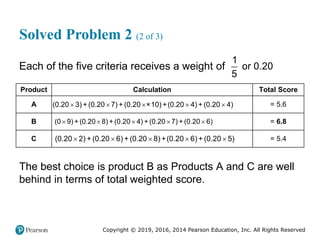
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Solved Problem 2 (3 of 4)
Figure 2.17 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-107-320.jpg)



























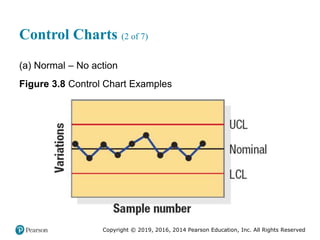
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Control Charts (3 of 7)
(b) Run – Take action
Figure 3.8 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-141-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Control Charts (4 of 7)
(c) Sudden change – Monitor
Figure 3.8 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-142-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Control Charts (5 of 7)
(d) Exceeds control limits – Take action
Figure 3.8 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-143-320.jpg)




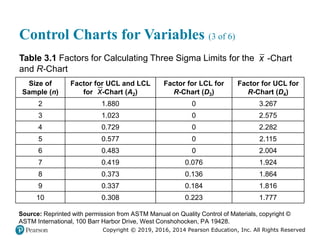
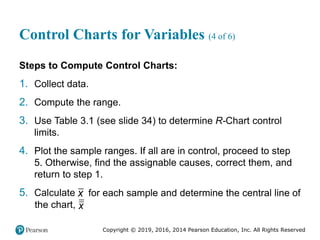

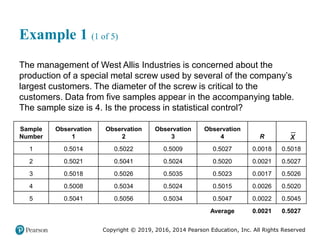

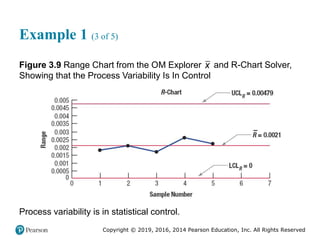

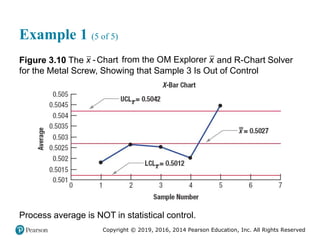










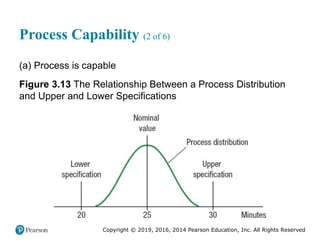
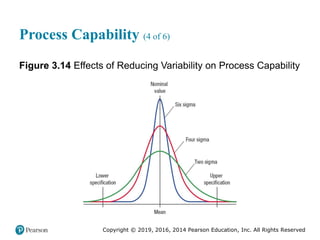
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Process Capability (3 of 6)
(b) Process is not capable
Figure 3.13 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-170-320.jpg)















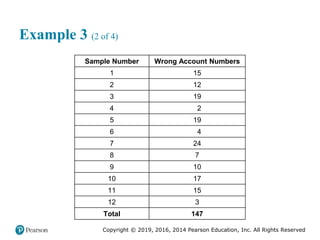
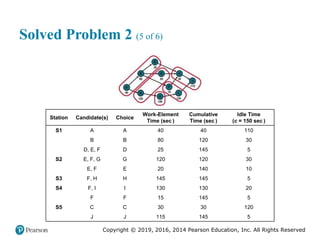
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
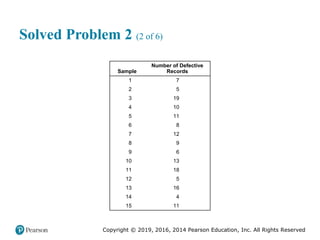
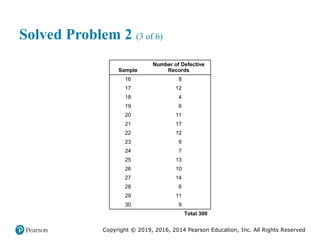
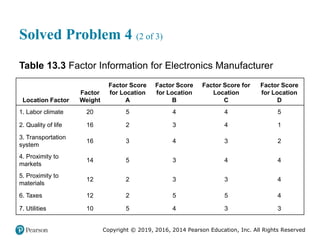
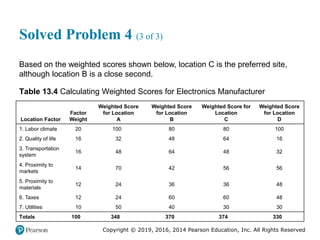
Solved Problem 2 (5 of 6)
a. From the table, the supervisor knows that the total number of
defective records is 300 out of a total sample of 7,500 [or 30(250)].
Therefore, the central line of the chart is
300
= = 0.04
7,500
p
The control limits are:
(1 ) 0.04(0.96)
UCL = + z = 0.04 + 3 = 0.077
250
(1 ) 0.04(0.96)
LCL = = 0.04 3 = 0.003
250
p
p
p p
p
n
p p
p z
n](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-190-320.jpg)














![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Capacity Timing and Sizing (2 of 2)
Figure 4.2 [continued]
(b) Wait-and-see strategy](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-209-320.jpg)


![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Step 1 - Estimate Capacity Requirements (1 of 2)
For one service or product processed at one operation with a one year time
period, the capacity requirement, M, is
Processinghours required for year's demand
Capacity requirement =
Hours available from a single capacity unit
(such as an employee or machine) per year,
after deducting desired cushion
[1 ( 100)]
Dp
M
N C
where
D = demand forecast for the year (number of customers served or units
produced)
p = processing time (in hours per customer served or unit produced)
N = total number of hours per year during which the process operates
C = desired capacity cushion (expressed as a percent)
M = the number of input units required](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-212-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Step 1 - Estimate Capacity Requirements (2 of 2)
Setup times (time required to change a process or an operation
from making one service or product to making another) may be
required if multiple products are produced
Processing and setup hours required for year s demand,
summed over all services or products
Capacity requirement =
Hours available from a single capacity unit per year,
after deducting desired cushion
M
product 1 product 2 product
[ ( ) ] [ ( ) ] [ ( ) ]
[1 ( 100)]
n
Dp D Q s Dp D Q s Dp D Q s
N C
Where
Q = number of units in each lot
s = setup time in hours per lot](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-213-320.jpg)
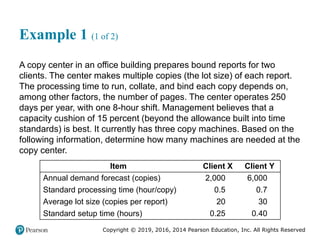
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 1 (2 of 2)
product 1 product 2 product n
client X client Y
[ ( ) ] [ ( ) ] [ ( ) ]
[1 ( 100)]
[2,000(0.5) (2,000 20)(0.25)] [6,000(0.7) (6,000 30)(0.40)]
[(250 day year)(1 shift day)(8 hours shift)][1.0 (15 100
Dp D Q s Dp D Q s Dp D Q s
M
N C
)]
5,305
1,700
3.12
Rounding up to the next integer gives a requirement of four
machines.](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-215-320.jpg)




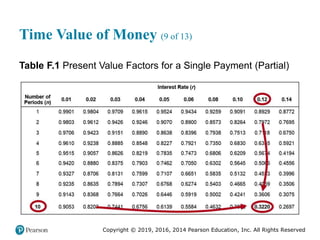
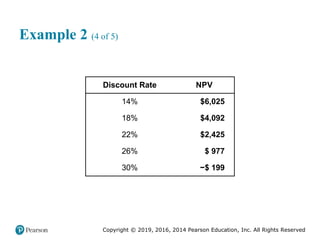
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (3 of 3)
• The owner should account for the time value of money,
applying such techniques as the net present value or internal
rate of return methods (see Supplement F, “Financial
Analysis,” in MyOMLab).
• For instance, the net present value (NPV) of this project at a
discount rate of 10 percent is calculated here, and equals
$13,051.76.
$13,051.76
2
3 4 5
200,000 [(20,000 1.1)] [40,000 (1.1) ]
[60,000 (1.1) ] [80,000 (1.1) ] [100,000 (1.1) ]
$200,000 $18,181.82 $33,057.85 $45,078.89
$54,641.07 $62,092.13
NPV
](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-220-320.jpg)

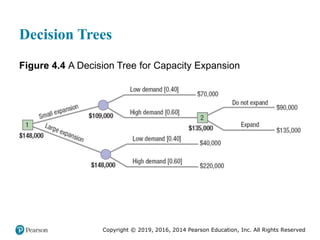
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Solved Problem 1 (2 of 4)
a. The number of hours of operation per year, N, is N = (2
shifts/day)(8 hours/shifts) (250 days/machine-year) = 4,000
hours/machine-year
The number of machines required, M, is the sum of machine-
hour requirements for all three products divided by the
number of productive hours available for one machine:
men women children
[ ( ) ] [ ( ) ] [ ( ) ]
[1 ( 100)]
[80,000(0.05) (80,000 240)0.5] [60,000(0.10) (60,000 180)2.2]
[120,000(0.02) (120,000 360)3.8]
4,000[1 (5 100)]
14,567 hours year
3,800 hours machin
Dp D Q s Dp D Q s Dp D Q s
M
N C
e year
3.83 or 4 machines](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-225-320.jpg)



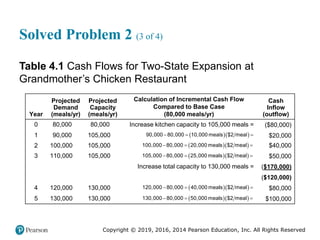
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Solved Problem 2 (4 of 4)
For comparison purposes, the NPV of this project at a discount
rate of 10 percent is calculated as follows, and equals negative
$2,184.90.
$2,184.90
2
3 4 5
80,000 (20,000 1.1) [40,000 (1.1) ]
[120,000 (1.1) ] [80,000 (1.1) ] [100,000 (1.1) ]
$80,000 $18,181.82 $33,057.85 $90,157.77
$54,641.07 $62,092.13
NPV
• On a purely monetary basis, a single-stage expansion seems
to be a better alternative than this two-stage expansion.
• However, other qualitative factors as mentioned earlier must
be considered as well.](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-231-320.jpg)



















































![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
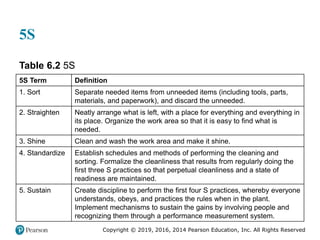
Continuous Improvement Using a Lean
Systems Approach (3 of 5)
Table 6.1 [continued]
Waste Definition
5. Motion Unnecessary effort related to the ergonomics of bending, stretching, reaching,
lifting, and walking. Jobs with excessive motion should be redesigned.
6. Inventory Excess inventory hides problems on the shop floor, consumes space,
increases lead times, and inhibits communication. Work-in-process inventory is
a direct result of overproduction and waiting.
7. Defects Quality defects result in rework and scrap and add wasteful costs to the system
in the form of lost capacity, rescheduling effort, increased inspection, and loss
of customer goodwill.
8. Underutilization
of Employees
Failure of the firm to learn from and capitalize on its employees’ knowledge and
creativity impedes long-term efforts to eliminate waste.](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-297-320.jpg)








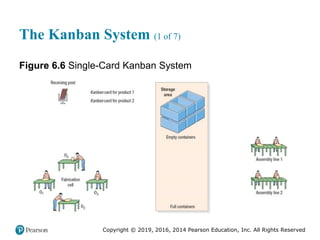
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Kanban System (2 of 7)
Figure 6.6 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-312-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Kanban System (3 of 7)
Figure 6.6 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-313-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Kanban System (4 of 7)
Figure 6.6 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-314-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Kanban System (5 of 7)
Figure 6.6 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-315-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Kanban System (6 of 7)
Figure 6.6 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-316-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
The Kanban System (7 of 7)
Figure 6.6 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-317-320.jpg)










![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (3 of 7)
Table 6.3 [continued]
Overall Process Attributes
Average demand: 3,200/week (1,000 “L”; 2,200 “S”)
Batch size: 40
Number of shifts per day: 1
Availability: 8 hours per shift with two 30-minute lunch breaks
Customer Shipments One shipment of 3,200 units each week in trays of 40 pieces
Information Flow All communications from customer are electronic:
180/90/60/30/day Forecasts
Daily Order
All communications to supplier are electronic
4-Week Forecast
Weekly Fax
There is a weekly schedule manually delivered to Press, Pierce & Form, and
Finish Grind and a Daily Ship Schedule manually delivered to Shipping
All material is pushed](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-330-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (5 of 7)
b. Daily Demand
[(1,000 + 2,200) pieces/week]/5 days = 640 pieces per day
Daily Availability
(7 hours/day) × (3,600 seconds per hour) = 25,200
seconds per day
Takt Time
Daily availability 25,200
= = =
Daily Demand 640
39.375 seconds per piece](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-332-320.jpg)



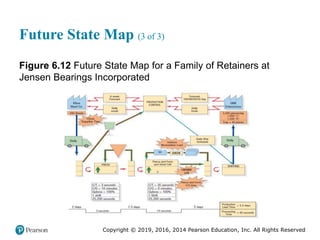






![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
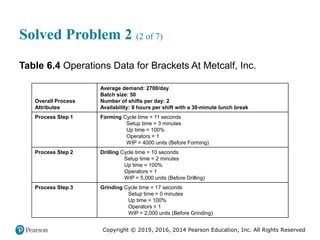
Solved Problem 2 (3 of 7)
Table 6.4 [continued]
Overall Process
Attributes
Average demand: 2700/day
Batch size: 50
Number of shifts per day: 2
Availability: 8 hours per shift with a 30-minute lunch break
Process Step 4 Packaging Cycle time = 15 seconds
Setup time = 0 minutes
Up time = 100%
Operators = 1
WIP = 1,600 units (Before Packaging)
WIP = 15,700 units (Before Shipping)
Customer Shipments One shipment of 13,500 units each week
Information Flow All communications with customer are electronic
There is a weekly order release to Forming
All material is pushed](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-345-320.jpg)
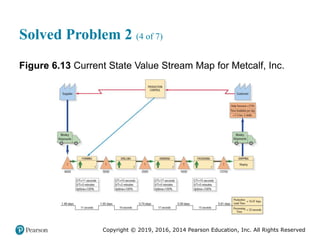














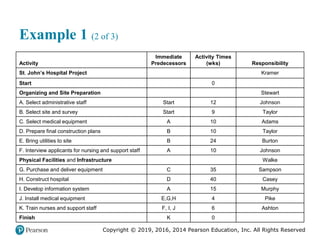
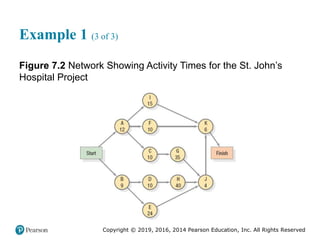


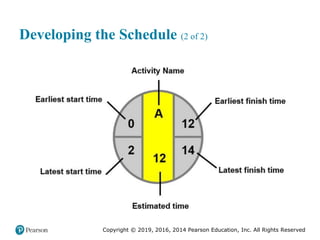

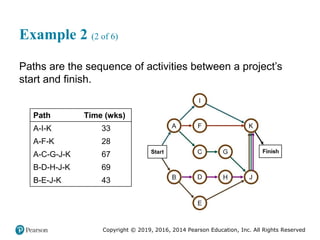
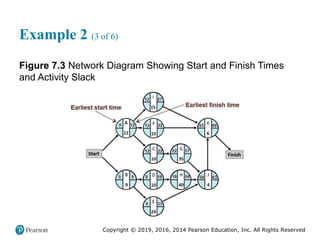
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (4 of 6)
Figure 7.3 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-370-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (5 of 6)
Figure 7.3 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-371-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (6 of 6)
Figure 7.3 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-372-320.jpg)








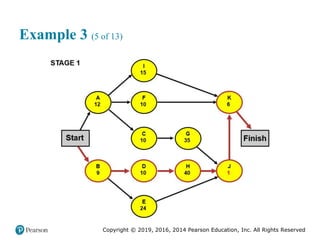


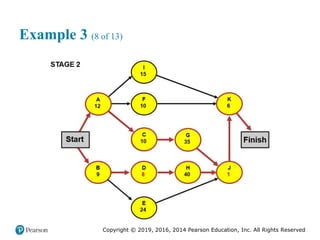

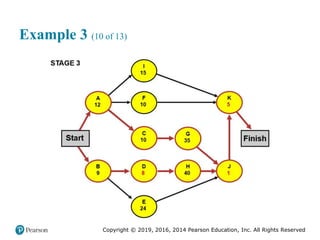

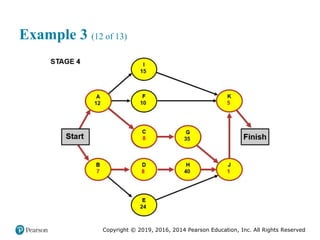
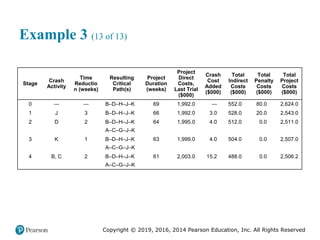






















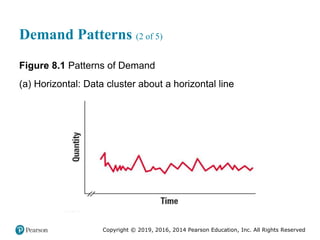
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Demand Patterns (3 of 5)
Figure 8.1 [continued]
(b) Trend: Data consistently increase or decrease](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-427-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Demand Patterns (4 of 5)
Figure 8.1 [continued]
(c) Seasonal: Data consistently show peaks and valleys](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-428-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Demand Patterns (5 of 5)
Figure 8.1 [continued]
(d) Cyclical: Data reveal gradual increases and decreases over
extended periods](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-429-320.jpg)































































































































































![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
MRP Explosion (3 of 8)
Figure 11.10 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-653-320.jpg)














![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Outputs from MRP (5 of 8)
Figure 11.18 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-674-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Outputs from MRP (6 of 8)
Figure 11.18 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-675-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Outputs from MRP (7 of 8)
Figure 11.18 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-676-320.jpg)








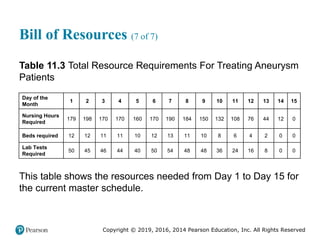











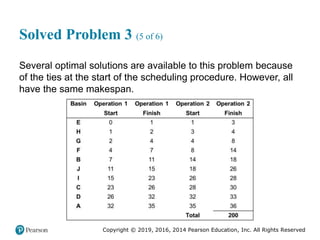
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Solved Problem 3 (4 of 5)
Figure 11.27 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-703-320.jpg)
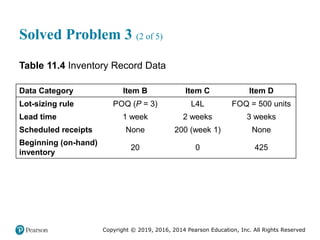
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Solved Problem 3 (5 of 5)
Figure 11.27 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-704-320.jpg)

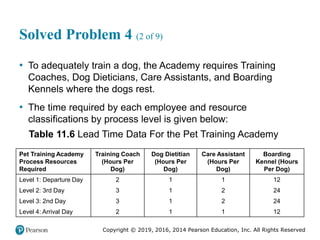













































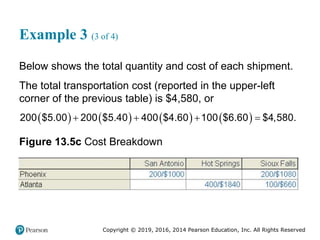
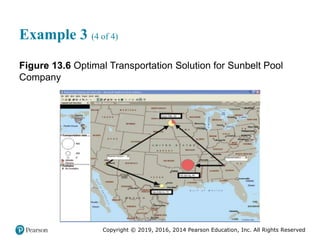































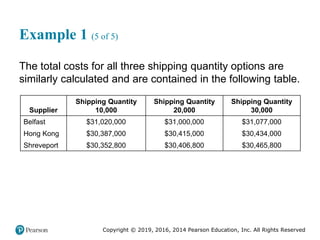

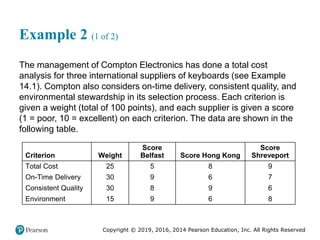





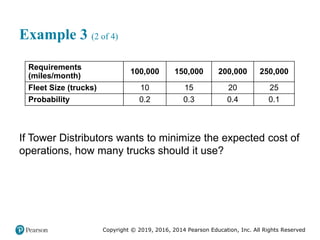






![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
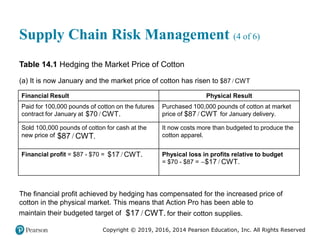
Supply Chain Risk Management (5 of 6)
Table 14.1 [continued]
(b) It is now June and the market price of cotton has dropped to /
$65 CWT.
Financial Result Physical Result
Paid $70 per C W T for 100,000 pounds of cotton
on the futures contract for the month of June.
Purchased 100,000 pounds of cotton at the
market price of $65 per C W T for June delivery.
Sold 100,000 pounds of cotton for cash at the
new price of $65 per C W T.
It is now less expensive to produce the cotton
apparel.
Financial loss = $65 - $70 = $5 per C W T. Physical loss in profits relative to budget
= $70 - $65 = $5 per C W T.
The financial loss is balanced by the increase in physical profits. Active Pro has
achieved the budgeted cost of / .
$70 CWT
/ .
$5 CWT
/ .
$5 CWT
/
$65 CWT.
/
$65 CWT
/
$70 CWT](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-841-320.jpg)






































































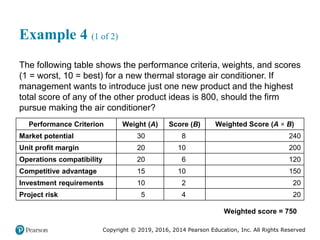
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
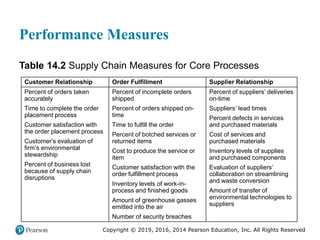
Example 2
If the most pessimistic sales forecast for the proposed
service from Figure A.1 was 1,500 patients, what would be
the procedure’s total contribution to profit and overhead per
year?
( ) ( ) [ (
+ = 200 1,500 100,000 +100 1,500
= $
)
50,000
]
pQ F cQ](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-925-320.jpg)





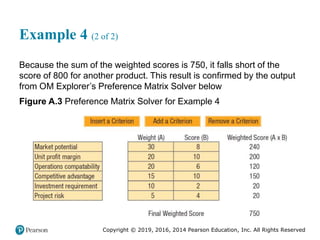












![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 8 (3 of 8)
Figure A.5 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-948-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 8 (4 of 8)
Figure A.5 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-949-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 8 (5 of 8)
Figure A.5 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-950-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 8 (6 of 8)
Figure A.5 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-951-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 8 (7 of 8)
Figure A.5 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-952-320.jpg)
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 8 (8 of 8)
Figure A.5 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-953-320.jpg)


![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Solved Problem 1 (4 of 4)
b. Total profit contribution = Total revenue − Total cost
[ ]
= +
=15(10,000) 56,000 + 7(10,000)
= $
( )
24,000
pQ F cQ](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-957-320.jpg)











![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 1
• Management is redesigning the customer service process in a large
department store.
• Accommodating four customers is important.
• Customers arrive at the desk at the rate of two customers per hour.
• What is the probability that four customers will arrive during any
hour?
In this case customers per hour, T = 1 hour, and n = 4 customers. The
probability that four customers will arrive in any hour is
4
2(1) 2
4
[2(1)] 16
0.090
4! 24
P e e
](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-979-320.jpg)





























































































































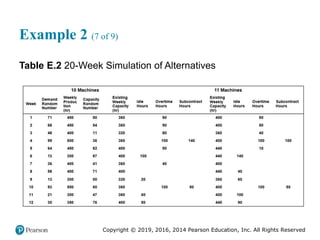
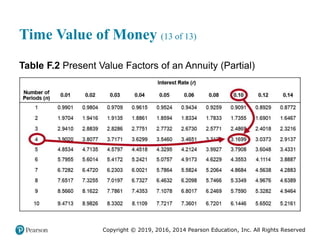
![Copyright © 2019, 2016, 2014 Pearson Education, Inc. All Rights Reserved
Example 2 (8 of 9)
Table E.2 [continued]](https://image.slidesharecdn.com/krajewskiom1201-231029185205-c0880f92/85/krajewski_om12-_01-pptx-1134-320.jpg)