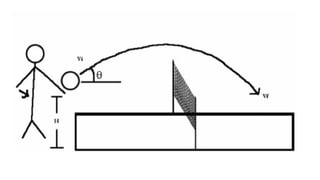
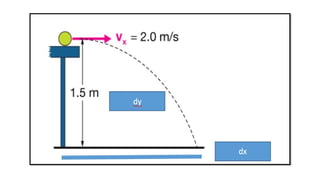
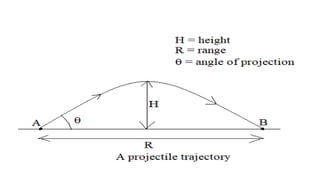
The document explains the concepts of kinematics and dynamics, focusing on motion, distance, displacement, speed, velocity, and acceleration. It includes sample problems demonstrating these concepts, such as calculating distances traveled and accelerations. Additionally, it covers projectile motion and free fall, illustrating how objects move under the influence of gravity and air resistance.

1. Kinematics
and Dynamics

5. MOTION

6. KINEMATICS
DYNAMICS

7. •Describes motion in terms of
displacement, velocity, and
acceleration.
KINEMATICS

8. •Is the study of force in relation to motion.
DYNAMICS

9. •Is the term used in physics for motion in
straight line. Here, we shall consider the
origin of the Cartesian coordinate
system as the origin of motion. Motion
directed to the right is always positive,
while those that are directed to the left
of the origin is considered negative.
TRANSLATION

10. DISTANCE AND
DISPLACEMENT

11. DISTANCE
•Refers to the total length of
path taken by an object in
moving from its initial to final
position.

12. DISPLACEMENT
•Refers to the straight line
distance between an object’s
initial and final positions, with
direction toward the final
position.

13. SAMPLE PROBLEM
•Starting from the church, a procession has to
take the following route: 50 m, north; 40 m
east; and 60 m, north. To go back, it has to
follow the same route but in the opposite
direction. (a) What is the total distance traveled?
(b). What is the total displacement?

14. SPEED VS VELOCITY

16. SPEED
•Is the distance traveled by a
body in a given time. Speed is
a scalar quantity.

17. Velocity
•Is the time rate of change of
position. It is the displacement of a
body in a specified time interval.

19. Sample Problem
Edrian and Emmanuel who are 150 m
apart start walking toward each other at
3 m/s and 5 m/s, respectively. (a) How
long will it take them to meet? (b) Find
the corresponding distance travelled by
each.

20. Certainly, let's solve this step-by-step:
(a) To calculate the time it takes for to meet, we can use the formula:
(b) Given information:
- Distance between Lean and Mickey = 150m
- Speed of Emmanuel = 3m/s
- Speed of Edrian = 5m/s

21. (b) To find the distance traveled by each
person, we can use the time calculated in
part (a) and their respective speeds.
Distance traveled by Lean = Speed of
Lean × Time

22. Acceleration
•Is the rate of change of velocity.
Since velocity is a vector quantity, a
change in velocity can be a change
in magnitude, a change in direction,
or change in both magnitude and
direction.

23. • The simplest type of accelerated motion with constant acceleration.
In equation form.

24. Uniformly Accelerated Motion
• The descriptors of motion discussed so far are time, displacement, and
velocity.
• Let…
•a – acceleration (m/
•t – time (s)
•- final velocity (m/s)
•- initial velocity (m/s)
•d – displacement (m)

25. Using these variables and
other concepts, we will now
proceed to derive the four
equations of uniformly
accelerated motion.

26. EQUATION 1
• a =
Do algebraic manipulations:
•at =
•at + =
• = + at

27. EQUATION 2
•If the velocity v is constant, the displacement d is
computed by multiplying velocity by the time: d = vt
•If the velocity is not constant, we use the average
velocity, to compute for the displacement d
d = x t ; but = so; d = () t

28. EQUATION 3
• t =
•= + 2ad

29. EQUATION 4
•d = + a

31. •A car covers 200.0 m while
increasing its velocity from 20.0 m/s
to 30.0 m/s. Compute the
acceleration.

32. •Starting from rest, a car
accelerates at +2.0 m/ How far
will it go after 6.0 s?

33. •A car accelerates at a constant
rate from 15 m/s to 25 m/s
while it travels 125 m. How long
does it take to achieve this
speed?

35. FREE FALL

36. •In the absence of air
resistance, all bodies at the
same location above Earth’s
surface fall vertically with the
same acceleration regardless
of their sizes and mass.

37. •This idealized motion of a
falling object, which is acted
upon only by the force of
gravity, is called free fall.

38. •The acceleration of a free-falling body is
called acceleration due to gravity denoted
gravity denoted by “g” and is equal and is
equal to 9.8 m/. This acceleration is
downward and directed toward Earth’s
center.

39. What causes some bodies to fall
faster than others, even though they
have the same mass?
•The answer is air resistance. A falling body
collides with countless particles of air,
slowing down its fall. Generally, the faster
the speed and the greater the surface area,
the more air resistance a falling body
encounters.

43. SAMPLE PROBLEM:
•A rocket ship far from any star
or planet accelerates uniformly
from 65 m/s to 162 m/s in 10.0
s. How far does it move?

44. •Filipinos young and old, play basketball with all
their hearts. This shows the Filipinos undying
love for basketball. Every summer, there is a
basketball league in every barangay. However,
what Filipinos should also know is that
basketball is more than just a sport.

45. •This sport demonstrates a lot of physics
concepts. One of which is the projectile
motion, a type of motion wherein an object
called a projectile is thrown in the air, and
moves a curved path under gravity alone.

46. •In basketball, when the ball is
thrown to the basket, the ball
moves along a parabolic path. This
is an example of non-horizontally
launched projectile with vertical
motion. Wherein the ball is released
at an angle.

47. Projectile Motion
•Is a two-dimensional type of motion
which consists of two independent parts:
uniform motion (zero acceleration) along
the horizontal and uniformly accelerated
motion along the vertical which is
similar to the free fall.

50. FORMULA

51. Events which show projectile motion:
A volleyball serve
A three point attempt in
basketball,
Javelin and discuss throw

52. •The Volleyball, Basketball, and
Javelin throws are called the
projectiles. The shape of the
path of a projectile is a parabola.

56. • 1. You decided to play “Flick the coin” with your friend. The
goal of the game is to flick the coin from the top of a table
and let it land on the floor as far as possible. The coin that
you flicked left the table (0.60 m high) with an initial
horizontal velocity of 3 m/s. Compute the following:
• a. Time it will take for the coin to reach the ground.
• b. Range (how far from the base of the table will the coin
land)
• (Note that the time it takes for the balls to reach the range
and the time it takes for the ball to reach the floor when it is
dropped straight downward are equal)

57. •A ball rolling on a table top, which
follows a parabolic path before
falling to the ground, is an example
of a horizontally launched
projectile. In this case, the ball was
not released at an angle.

58. •A pebble is thrown horizontally at 15 m/s from
the top of a building 44 m high.
a. How far from the base of the building does the
pebble hit the ground?
b. How long is it moving the instant before it hits
the ground?