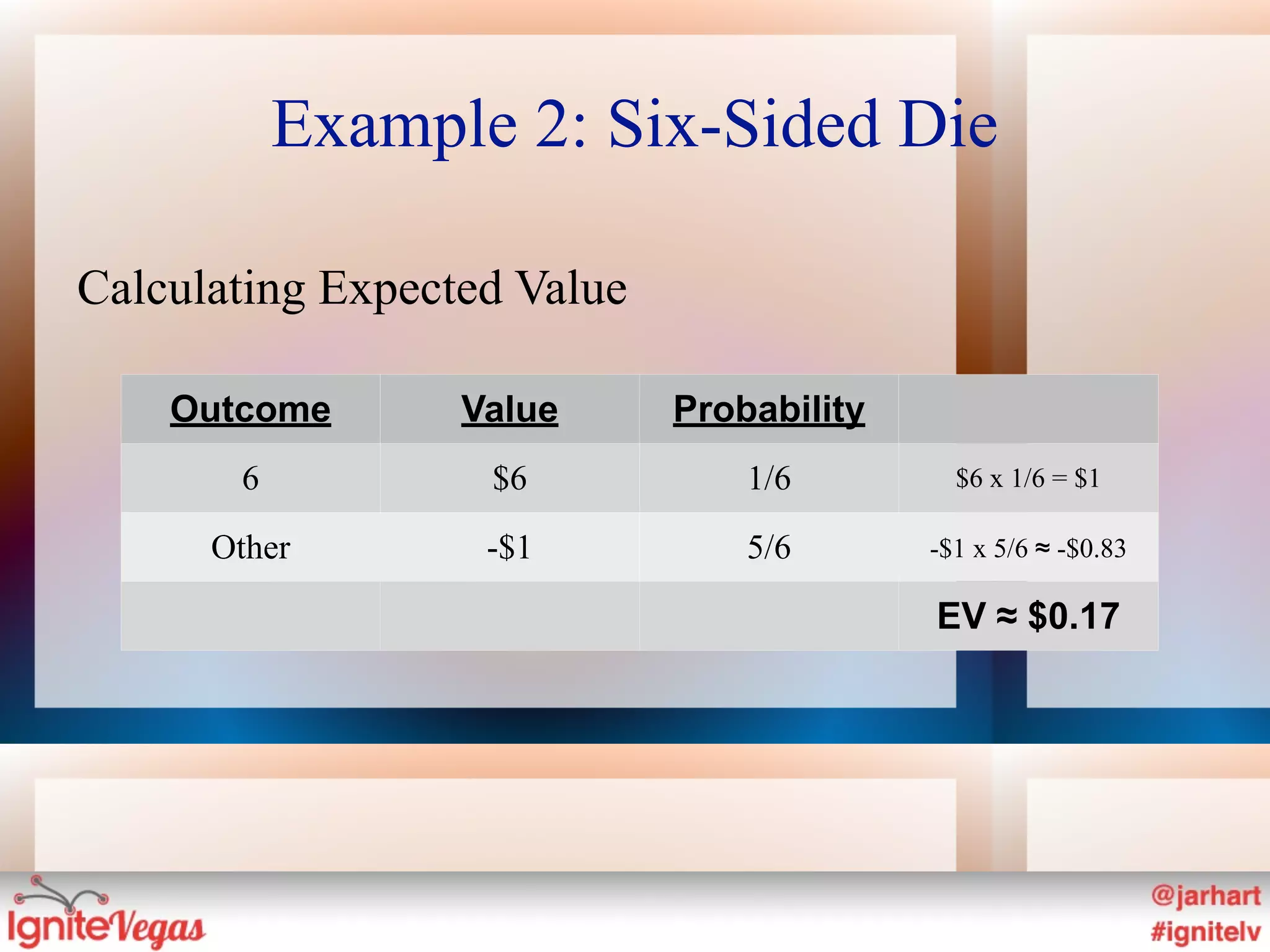
The document discusses the concept of expected value (EV) in gambling theory, explaining how it quantifies the average outcome of various scenarios. It illustrates EV using examples like a coin flip and a six-sided die, emphasizing the importance of this concept in decision-making and its relevance to real-life situations. Additionally, the document touches on insurance and extended warranties, stating that they often have a negative expected value for consumers.

1. Why Gambling Theory Matters

2. Expected Value (EV)
 Weighted average of all possible outcomes
 Quantifies what you can expect to gain, on average
 A fundamental concept in gambling theory...
 And in life

3. Example 1: A Coin Flip Game
 Two-player game
 We each put $1 on a table
 You flip a coin
Heads: you win the money on the table
Tails: I win the money on the table

4. Example 1: A Coin Flip Game
 Probability is 50/50
 Heads: you win $1
 Tails: you lose $1
You can expect to break even on average.
The expected Value is $0.

5. Calculating Expected Value
 Consider all possible outcomes
 Multiply the value of each outcome by the probability
of that outcome
 Add up all of those products
 The result is the expected value

6. Example 1: A Coin Flip Game
Calculating Expected Value
Outcome Value Probability
Heads $1 0.5 $1 x 0.5 =
Tails -$1 0.5 $0.50
-$1 x 0.5 =
-$0.50
EV = $0

8. Using EV to Make Decisions
 Consider all of your options
 Calculate the expected value of each option
 Choose the option with the highest EV
In many cases your decision is simply
whether or not to gamble.

9. Example 2: Six-Sided Die
 You put $1 on the table
 I put $6 on the table
 You roll a 6-sided die
Roll a 6, you win the money on the table
Roll anything else, I win the money on the table

10. Example 2: Six-Sided Die
 You only win if you roll a
six
 You are five times as
likely to lose as to win
You can expect to lose most of the time.
Should you play this game?

11. Example 2: Six-Sided Die
Calculating Expected Value
Outcome Value Probability
6 $6 1/6 $6 x 1/6 = $1
Other -$1 5/6 -$1 x 5/6 ≈ -$0.83
EV ≈ $0.17

12. Life Is Gambling
 In the last example, even though you are five times as
likely to lose, the expected value is a win.
 If you played the game repeatedly, over time you could
reasonably expect to win an average of (almost) $0.17
per game.
Many decisions in life resemble this game

13. Life Is Gambling
 Most sales contacts don't result in a sale.
 Most start-ups fail.
 Most movies lose money at the box office.
 There are many more examples.
These games are winnable if you keep playing.

15. Insurance
 For when the worst case is unacceptable
 You accept a lower EV in exchange for a better worst
case scenario
 It is almost always a mistake to insure what you can
reasonably cover yourself

16. Insurance
 For when the worst case is unacceptable
 You accept a lower EV in exchange for a better worst
case scenario
 It is almost always a mistake to insure what you can
reasonably cover yourself
Not all insurance is called insurance!

17. When Insurance Isn't Called Insurance

18. Extended Warranties
 Extended warranties are a type of insurance
 Usually 10% of the cost of the item
 In most cases you could replace it yourself
 Unless you are more than 10% likely to need the item
replaced within the warranty period, purchasing the
warranty is -EV.

19. Extended Warranties
 Extended warranties are a type of insurance
 Usually 10% of the cost of the item
 In most cases you could replace it yourself
 Unless you are more than 10% likely to need the item
replaced within the warranty period, purchasing the
warranty is -EV.
 Selling extended warranties is +EV for the stores,
otherwise they wouldn't sell them.

20. Gambling Theory Matters