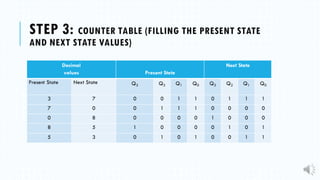
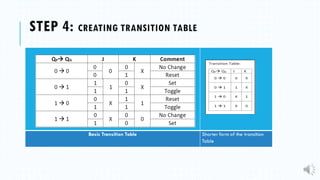
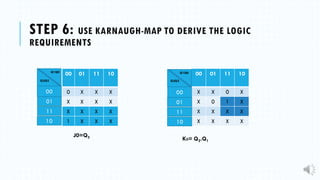
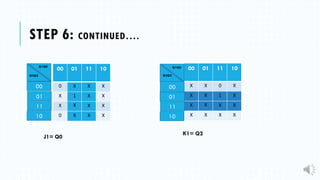
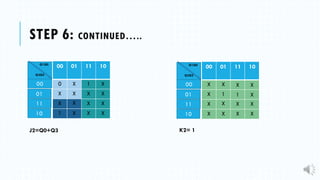
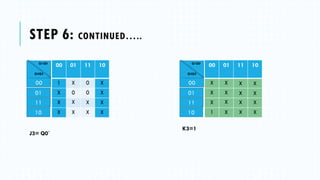
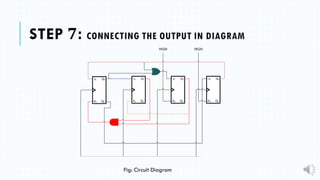
This document describes the design of an irregular counter sequence using 4 flip-flops. It involves the following steps: 1) Converting the decimal sequence into binary. 2) Determining 4 flip-flops are needed to represent the maximum value of 8. 3) Creating a counter table to determine the present and next state binary values. 4) Deriving the logic equations using Karnaugh maps. 5) Connecting the flip-flops and generating the circuit diagram based on the logic equations.

1. IRREGULAR SEQUENCE
COUNTER
Name: Abdullah Al Mamun Shiam Sub: Digital Logic Design
ID: 18-37075-1 Sec: C

2. THE PROBLEM
 My id is – 18-37075-1.
 I have to generate a counter sequence with the 5 middle digits of my id.
 ABCDE corresponds to 37075
 But the digit 7 is twice here so I have added 1 this to :
 3->7->0->7+1->5
=>3->7->0->8->5
A B C D E
3 7 0 8 5

3. STEP 1: BINARY OF THE DECIMAL SEQUENCE

4. STEP 2: IDENTIFYING THE NUMBER OF FLIP-FLOP
Here the maximum decimal value is 8. When we convert 8 to binary we get 1000 which is a 4 bit output. So, we’ll
require 4 flip-flops here to design our system.
J1 Q1
K1 Q1ˊ
J1 Q1
K1 Q1ˊ
J2 Q2
K2 Q2ˊ
J3 Q3
K3 Q3ˊ

5. STEP 3: COUNTER TABLE (FILLING THE PRESENT STATE
AND NEXT STATE VALUES)
Decimal
values Present State
Next State
Present State Next State Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0
3 7 0 0 1 1 0 1 1 1
7 0 0 1 1 1 0 0 0 0
0 8 0 0 0 0 1 0 0 0
8 5 1 0 0 0 0 1 0 1
5 3 0 1 0 1 0 0 1 1

6. STEP 4: CREATING TRANSITION TABLE
Basic Transition Table Shorter form of the transition
Table

7. STEP 5: FILLING UP THE VALUES OF J0, K0, J1, K1, J2, K2,
J3, K3
Decimal Present State Next State Inputs
Present
State
Next
State
Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0 J0 K0 J1 K1 J2 K2 J3 K3
3 7 0 0 1 1 0 1 1 1 X 0 X 0 1 X 0 X
7 0 0 1 1 1 0 0 0 0 X 1 X 1 X 1 0 X
0 8 0 0 0 0 1 0 0 0 0 X 0 X 0 X 1 X
8 5 1 0 0 0 0 1 0 1 1 X 0 X 1 X X 1
5 3 0 1 0 1 0 0 1 1 X 0 1 X X 1 0 X
Q
P
Q
N
J K
0 0 0 X
0 1 1 X
1 0 X 1
1 1 X 0

8. STEP 6: USE KARNAUGH-MAP TO DERIVE THE LOGIC
REQUIREMENTS
00 01 11 10
0 X X X
X X X X
X X X X
1 X X X
00
01
11
10
J0=Q3
Q1Q0
Q3Q2
K0= Q2.Q1
00 01 11 10
X X 0 X
X 0 1 X
X X X X
X X X X
00
01
11
10
Q3Q2
Q1Q0

9. STEP 6: CONTINUED….
00 01 11 10
0 X X X
X 1 X X
X X X X
0 X X X
00
01
11
10
J1= Q0
K1= Q2
Q1Q0
Q3Q2
00 01 11 10
X X 0 X
X X 1 X
X X X X
X X X X
00
01
11
10
Q3Q2
Q1Q0

10. STEP 6: CONTINUED…..
00 01 11 10
0 X 1 X
X X X X
X X X X
1 X X X
Q3Q2
00
01
11
10
J2=Q0+Q3 K2= 1
Q1Q0
00 01 11 10
X X X X
X 1 1 X
X X X X
X X X X
Q3Q2
00
01
11
10
Q1Q0

11. STEP 6: CONTINUED…..
K3=1
00 01 11 10
X X X X
X X X X
X X X X
1 X X X
Q3Q2
00
01
11
10
Q1Q0
00 01 11 10
1 X 0 X
X 0 0 X
X X X X
X X X X
Q3Q2
00
01
11
10
Q1Q0
J3= Q0ˊ

12. STEP 6: CONNECTIONS
The equations acquired from k-maps are as follows:
1. J0=Q3
2. K0= Q2.Q1
3. J1= Q0
4. K1= Q2
5. ​J2=Q0+Q3
6. K2= 1
7. J3= Q0ˊ
8. K3=1

13. STEP 7: CONNECTING THE OUTPUT IN DIAGRAM
J0 Q0
K0 Q0ˊ
J1 Q1
K1 Q1ˊ
J2 Q2
K2 Q2ˊ
J3 Q3
K3 Q3ˊ
HIGH HIGH
Fig: Circuit Diagram

14. FOR YOUR ATTENTION
THANK YOU