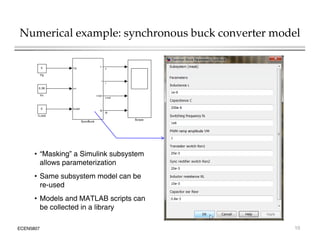
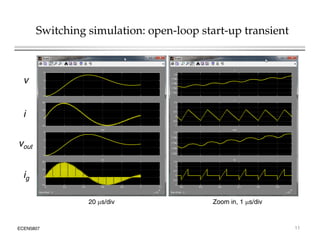
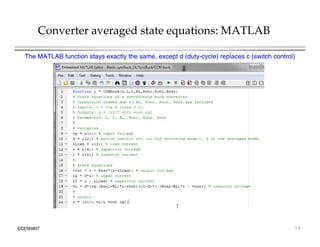
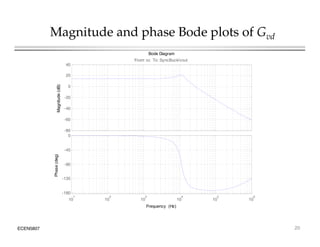
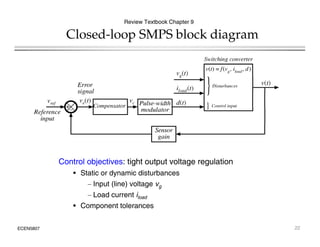
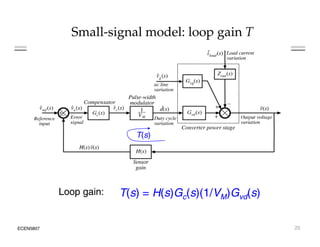
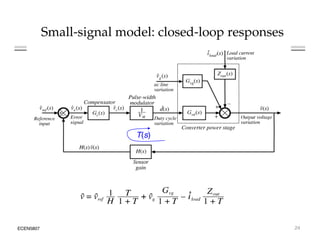
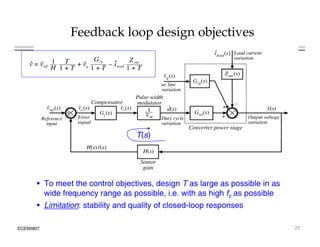
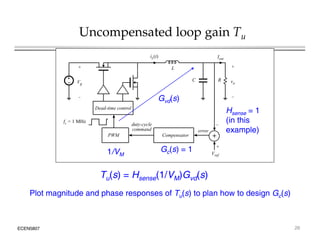
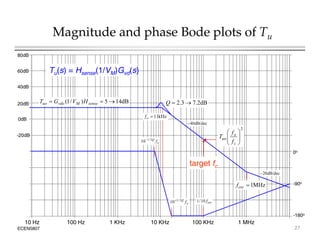
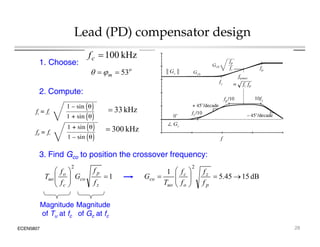
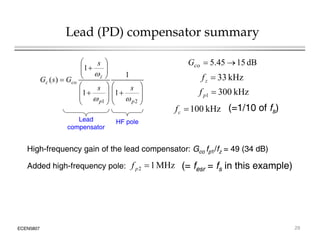
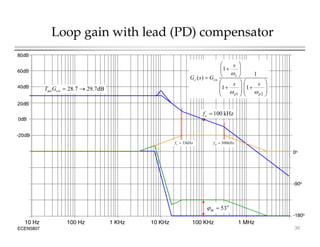
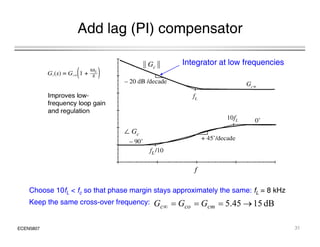
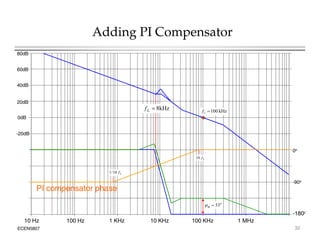
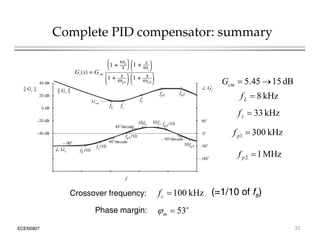
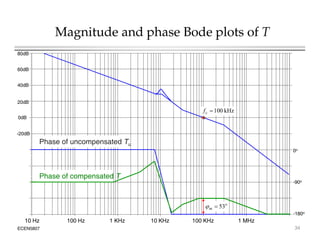
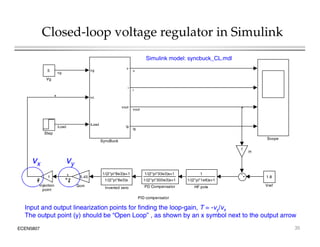
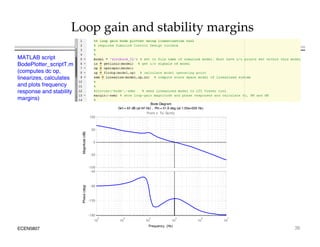
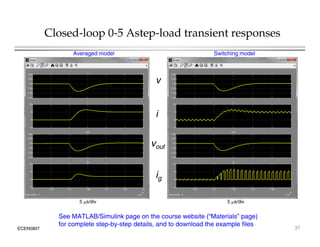
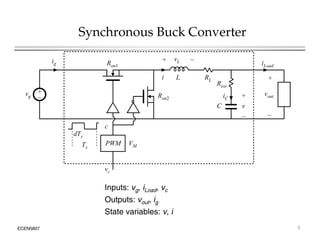
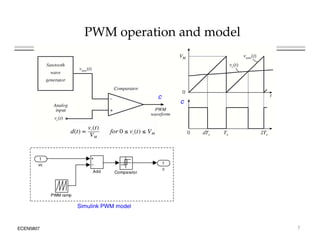
This document introduces switched-mode converter modeling using MATLAB/Simulink, focusing on building sophisticated control models and simulating systems within this environment. It highlights the unique capabilities of Simulink for system modeling while noting its limitations as a circuit simulator and the need for add-ons for traditional circuit simulations. Various aspects of modeling synchronous buck converters, including linearization and frequency response, are explored through examples and simulations.

1. Introduction to Switched-Mode Converter Modeling
using MATLAB/Simulink
• MATLAB: programming and scripting environment
• Simulink: block-diagram modeling environment inside MATLAB
Simulink: block diagram modeling environment inside MATLAB
• Motivation:
• Powerful environment for system modeling and simulation
• More sophisticated controller models, analysis and design tools
• But*:
• Block-diagram based Simulink models unidirectional signals
• Block-diagram based Simulink models, unidirectional signals
• Not a traditional circuit simulator; specialized physics-based Spice
device models or component libraries are not readily available
*Various add-ons to Simulink are available to allow traditional circuit diagram
entry and circuit simulations (e.g. SimPowerSystems, PLECS), or to embed
Spice within MATLAB/Simulink environment These add-ons are not required
ECEN5807 1
Spice within MATLAB/Simulink environment. These add-ons are not required
and will not be used in ECEN5807.

2. Introduction through an example
iLoad
ig
L R
Ron1
+
_
vL
i
Synchronous buck converter
+
–
vout
vg
+
_
Resr
C
+
_
v
L RL
Ron2 iC
i
Bode Diagram
40
-20
0
20
40
From: vc To: SyncBuck/vout
agnitude
(dB)
PWM
vc
dTs
Ts
VM
c
10
1
10
2
10
3
10
4
10
5
10
6
-180
-135
-90
-45
0
Phase
(deg)
-80
-60
-40
Ma
c
5
Vg
v g
v
i
v
• Switching model
• Averaged model
Frequency (Hz)
10 10 10 10 10 10
0
0.36
Vc
v c
iLoad
i
v out
ig
i
v out
• Small-signal linearization and
frequency responses
See MATLAB/Simulink page on the course
ECEN5807 2
iLoad
ig
SyncBuck
Scope
ig
Simulink model: syncbuck_OL.mdl
See MATLAB/Simulink page on the course
website (“Materials” page) for complete step-by-
step details, and to download the example files

3. Synchronous Buck Converter
iLoad
ig
+
L R
Ron1
+ _
vL
i
+
–
vout
vg
+
Resr
C
+
v
L RL
Ron2 iC
i
dTs
_
C
_
v
c
PWM
v
Ts
VM
vc
Inputs: vg, iLoad, vc
Outputs: vo t ig
ECEN5807 3
Outputs: vout, ig
State variables: v, i

4. Converter state equations
iLoad
ig
+
R
L RL
Ron1
+ _
vL
i
+
–
vout
vg
_
Resr
C
+
_
v
Ron2 iC
PWM
dTs
Ts
VM
c
vc
State equations Output equations
 
  )
0
(
)
1
(
2
1













c
c
v
i
R
R
v
i
R
R
v
dt
di
L
v
out
L
on
out
L
on
g
L
d
)
0
(
)
1
(
0 





c
c
i
ig
ECEN5807 4
Load
C i
i
dt
dv
C
i 

  
Load
esr
out i
i
R
v
v 



5. Simulink
model 5
Vg
v g
v
v
SyncBuck subsystem block
0
0.36
Vc
v c
iL d
i
v out
i
v out
0
iLoad
iLoad
ig
SyncBuck
Scope
ig
1
v
1
s
capacitor integrator
v c c
2
1
vg
dv /dt v
c
SyncBuck
subsystem
block
internals
3
2
i
1
s
inductor integrator
PWM
u y
CCMbuck
CCM buck
3
iLoad
vc
i
di/dt
v out
y
u
c
4
ig
vout
v out
ig
ECEN5807 5

6. Synchronous buck (SyncBuck) subsystem
1
vg
Integration of
state variables
PWM
2
1
v
1
1
s
capacitor integrator
v c c
PWM
2
vc
vg
dv /dt v
c
c
Inputs
PWM
subsystem
3
vout
2
i
s
inductor integrator
PWM
u y
CCMbuck
CCM buck
3
iLoad
i
di/dt
v out
y
u Outputs
4
ig
vout
ig
Converter
state
equations
ECEN5807 6

7. PWM operation and model
c
c
1
c
Add
1
vc
c
PWM ramp
Comparator
Add
ECEN5807 7
Simulink PWM model

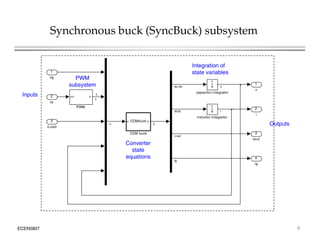
8. Converter state equations: embedded MATLAB script
1
3
vout
2
i
1
v
1
s
inductor integrator
1
s
capacitor integrator
v c c
PWM
u y
CCMbuck
CCM buck
3
iLoad
2
vc
1
vg
dv /dt v
i
di/dt
v out
y
u
c
c
u = inputs = [vg c iLoad v i]
y = outputs = [ic/C vL/L vout ig]
u y
4
ig
ig
Converter
state
equations
 
i
i
R
v
v 
)
0
(
)
1
(
0 





c
c
i
ig
 
Load
esr
out i
i
R
v
v 


  )
1
(
1 

 

 c
v
i
R
R
v
di
L out
L
on
g
Load
C i
i
dt
dv
C
i 


ECEN5807 8
 
  )
0
(
)
(
2
1








c
v
i
R
R
dt
L
v
out
L
on
out
L
on
g
L

9. Numerical example
iLoad
ig
+
Resr
L RL
Ron1
+
_
vL
i
• Switching frequency:
fs = 1MHz
+
–
dT
vout
vg
_
esr
C
+
_
v
Ron2 iC
c
• Iout = 0
• Vg = 5 V
PWM
vc
dTs
Ts
VM • L = 1 H
• RL = 10 m
• Ron1 = Ron2 = 20 m
• C = 200 F
5
Vg
v g
v
i
v
• Resr = 0.8 m
• PWM ramp amplitude
VM = 1 V
0
0.36
Vc
v c
iLoad
i
v out
i
v out
ECEN5807 9
M
• Vc = 0.36, D = 0.36
0
iLoad
iLoad
ig
SyncBuck
Scope
ig
Simulink model: syncbuck_OL.mdl

10. Numerical example: synchronous buck converter model
5
Vg
v g
v
v
0
0.36
Vc
v c
iL d
i
v out
i
v out
0
iLoad
iLoad
ig
SyncBuck
Scope
ig
• “Masking” a Simulink subsystem
allows parameterization
• Same subsystem model can be
re-used
• Models and MATLAB scripts can
ECEN5807 10
p
be collected in a library

11. Switching simulation: open-loop start-up transient
v
i
vout
ig
Zoom in 1 s/div
20 s/div
ECEN5807 11
Zoom in, 1 s/div
20 s/div

12. Averaged model
 
  )
0
(
)
1
(
2
1













c
c
v
i
R
R
v
i
R
R
v
dt
di
L
v
out
L
on
out
L
on
g
L
dv
Switching model
Load
C i
i
dt
dv
C
i 


)
0
(
)
1
(
0 





c
c
i
ig
)
0
(
0 
 c
 
Load
esr
out i
i
R
v
v 


State-space averaging (review Textbook Sections 7.1-7.3)
v
d
 
     
 
s
s
s
s
s
s
s T
out
T
L
on
T
out
T
L
on
T
g
T
T
L v
i
R
R
d
v
i
R
R
v
d
dt
i
d
L
v 








 2
1 1
p g g ( )
s
s
s
s T
Load
T
T
T
C i
i
dt
v
d
C
i 


s
s
T
T
g i
d
i 
Large-signal
averaged model
ECEN5807 12
 
s
s
s
s T
Load
T
esr
T
T
out i
i
R
v
v 



13. Converter averaged state equations: MATLAB
The MATLAB function stays exactly the same, except d (duty-cycle) replaces c (switch control)
ECEN5807 13

14. Synchronous buck (SyncBuck) subsystem:
switching or averaged model
1
Integration of
state
variables
Inputs
2
1
v
1
sw
constant
1
s
capacitor integrator
1/VM
v c c
PWM
2
vc
vg
dv /dt v
d
c
3
vout
2
i
s
inductor integrator
Switch
1/VM
PWM Gain
u
y
CCMbuck
CCM buck
3
iLoad
i
di/dt
v out
y
u
d
Converter
4
ig
ig
Converter
state
equations
Outputs
Averaged
model of the
PWM
Outputs
ECEN5807 14

15. Start-up transient simulations
Switching model Averaged model
v
i
vout
ig
ECEN5807 15

16. Linearization of the large-signal averaged model
Large-signal (nonlinear) averaged model
Linearization at an operating point
L
Vg d
iL
RL
Linearization at an operating point
+
–
R
+
v
vg
+
–
D vg
D iL
Resr Small-signal
averaged
C
–
g
Io d
g
model
The small-signal model can be solved for all important converter transfer functions:
d
v
s
Gvd
ˆ
ˆ
)
(  vg
v
v
s
G
ˆ
ˆ
)
( 
l d
out
i
v
s
Z
ˆ
ˆ
)
( 
ECEN5807 16
d g
v load
i
Control-to-output Line-to-output Output impedance

17. Synchronous buck converter example
Review textbook Chapter 8
L
+
Vg d
iL
RL
d
v
s
G o
vd
ˆ
ˆ
)
( 
Buck SSM
+
–
C
R
+
v
–
vg
+
–
D vg
Io d
D iL
Resr
2
1
)
(



 esr
g
vd
s
V
s
G

d
Gvd(s)
2
1
1
)
(










o
o
g
vd
s
s
Q 

P i f l
dˆ
kHz
11
2
1


CL
fo
 dBV
14
V
5 

vdo
G
Pair of poles:
Low-frequency gain:
MHz
1
1
f
dB
2
.
7
3
.
2
/




L
esr
loss
R
R
C
L
Q 5
/


C
L
R
Qload
Q
Q
ESR zero:
ECEN5807
MHz
1
2


esr
esr
CR
f

dB
2
.
7
3
.
2
|| 




load
loss
load
loss
load
loss
Q
Q
Q
Q
Q
Q
Q
17

18. Magnitude and phase Bode plots of Gvd
60dB
80dB
(1/VM)Gvd(s)
20dB
40dB
dB
14
5
)
/
1
( 

M
vdo V
G dB
2
.
7
3
.
2 

Q
0dB
-20dB
Q
2
/
1
kHz
11

o
f
dB/dec
40

0o
o
Q
f
2
/
1
10
-90o
MHz
1

esr
f
f
10
/
1
Q
f
2
/
1
10
dB/dec
20

ECEN5807
100 KHz
10 KHz
1 KHz
100 Hz
10 Hz 1 MHz
-180o
esr
f
10
/
1
o
Q
f
10
18

19. Linearization and frequency responses in
MATLAB/Simulink
5
Vg
vg
v
vg
v
0.36
Vc
vc
i
vout
vc
i
vout
1. Set transfer
function input
and output
points
0
iLoad
iLoad
ig
SyncBuck
Scope
iLoad
ig
2. MATLAB script (BodePlotter_script.m) computes DC operating point, linearizes the
p ( _ p ) p p g p ,
model, computes and plots the transfer function magnitude and phase responses
ECEN5807 19

20. Magnitude and phase Bode plots of Gvd
Bode Diagram
20
40
From: vc To: SyncBuck/vout
40
-20
0
20
agnitude
(dB)
0
-80
-60
-40
Ma
-90
-45
ase
(deg)
10
1
10
2
10
3
10
4
10
5
10
6
-180
-135
Pha
ECEN5807 20
Frequency (Hz)

21. Closed-loop (voltage-mode) control
Review Textbook Chapter 9
L
iL(t)
+ +
Iout
+
–
L
+
Vg
_
+
vo
_
C R
Dead-time control
_
fs = 1 MHz
duty-cycle
command
Vref
+
+
PWM Compensator
error
command
Gc(s)
1/VM = 1.8 V
Point-of-Load (POL) Synchronous Buck Regulator
ECEN5807 21

22. Closed-loop SMPS block diagram
Review Textbook Chapter 9
Control objectives: tight output voltage regulation
S i d i di b
• Static or dynamic disturbances
– Input (line) voltage vg
– Load current iload
ECEN5807
• Component tolerances
22

23. Small-signal model: loop gain T
T(s)
( )
Loop gain: T(s) = H(s)Gc(s)(1/VM)Gvd(s)
ECEN5807 23

24. Small-signal model: closed-loop responses
T(s)
( )
ECEN5807 24

25. Feedback loop design objectives
T(s)
( )
• To meet the control objectives, design T as large as possible in as
wide frequency range as possible, i.e. with as high fc as possible
ECEN5807
• Limitation: stability and quality of closed-loop responses
25

26. Uncompensated loop gain Tu
L
iL(t)
+ +
Iout
+
– Vg
_
vo
_
C
Dead time control
R
H 1
Gvd(s)
Dead-time control
_
+
PWM Compensator
fs = 1 MHz
error
duty-cycle
command
Hsense = 1
(in this
example)
Vref
+
Gc(s) = 1
1/VM
Tu(s) = Hsense(1/VM)Gvd(s)
Plot magnitude and phase responses of Tu(s) to plan how to design Gc(s)
ECEN5807 26

27. Magnitude and phase Bode plots of Tu
60dB
80dB
Tu(s) = Hsense(1/VM)Gvd(s)
20dB
40dB
dB
14
5
)
/
1
( 

 sense
M
vdo
uo H
V
G
T dB
2
.
7
3
.
2 

Q
0dB
-20dB
Q
2
/
1
kHz
11

o
f
dB/dec
40

2





 o
uo
f
f
T
0o
o
Q
f
2
/
1
10
target fc



 c
uo
f
-90o
MHz
1

esr
f
f
10
/
1
Q
f
2
/
1
10
dB/dec
20

ECEN5807
100 KHz
10 KHz
1 KHz
100 Hz
10 Hz 1 MHz
-180o
esr
f
10
/
1
o
Q
f
10
27

28. Lead (PD) compensator design
o
m 53

 

kHz
100

c
f
1. Choose:
kH
3
3
2. Compute:
kHz
3
3

kHz
00
3

2

 f
f 1
2

 f
f
3. Find Gco to position the crossover frequency:
1









z
p
co
c
o
uo
f
f
G
f
f
T dB
15
45
.
5
1











p
z
o
c
uo
co
f
f
f
f
T
G
ECEN5807
Magnitude
of Tu at fc
Magnitude
of Gc at fc
28

29. Lead (PD) compensator summary









1
1
)
(
z
s

dB
15
45
.
5 

co
G
kHz
33
f





















2
1
1
1
1
)
(
p
p
z
co
c
s
s
G
s
G


kHz
33

z
f
kHz
300
1 
p
f
kHz
100
f (=1/10 of f )
kHz
100

c
f (=1/10 of fs)
Lead
compensator
HF pole
MHz
1
2 
p
f (= fesr = fs in this example)
Added high-frequency pole:
High-frequency gain of the lead compensator: Gco fp1/fz = 49 (34 dB)
2
p ( esr s p )
g q y p
ECEN5807 29

30. Loop gain with lead (PD) compensator
60dB
80dB









1
1
)
( z
s
G
G

20dB
40dB dB
7
.
29
7
.
28 

co
uoG
T 




















2
1
1
1
)
(
p
p
co
c
s
s
G
s
G


0dB
-20dB
kHz
100

c
f
kHz
10

z
f
0o
kHz
300

p
f
kHz
33

z
f
-90o
ECEN5807
100 KHz
10 KHz
1 KHz
100 Hz
10 Hz 1 MHz
-180o
o
m 53


30

31. Add lag (PI) compensator
Integrator at low frequencies
Choose 10fL < fc so that phase margin stays approximately the same: fL = 8 kHz
Keep the same cross over frequency: dB
15
45
5
G
G
G
ECEN5807
Keep the same cross-over frequency: dB
15
45
.
5 



 cm
co
c G
G
G
31

32. Adding PI Compensator
60dB
80dB
20dB
40dB
kHz
8
f
0dB
-20dB
kHz
8

L
f kHz
100

c
f
0o
L
f
10
-90o
L
f
10
/
1
PI compensator phase
ECEN5807
100 KHz
10 KHz
1 KHz
100 Hz
10 Hz 1 MHz
-180o
o
m 53


32

33. Complete PID compensator: summary
dB
15
45
.
5 

cm
G
kHz
8

L
f
kHz
33

z
f
kHz
300
1 
p
f
MHz
1
2 
p
f
kHz
100

c
f (=1/10 of fs)
Crossover frequency:
ECEN5807
53o
m 

Phase margin:
33

34. Magnitude and phase Bode plots of T
60dB
80dB
20dB
40dB
0dB
-20dB
kHz
100

c
f
Ph f d T
0o
Phase of uncompensated Tu
-90o
Phase of compensated T
ECEN5807
100 KHz
10 KHz
1 KHz
100 Hz
10 Hz 1 MHz
-180o
o
m 53


34

35. Closed-loop voltage regulator in Simulink
5 vg
v
vg
v
Simulink model: syncbuck_CL.mdl
Vg
vc
i
vout
i
x
iLoad
vout
ig
Step
Scope
iLoad
vout
ig
SyncBuck
Scope
1
H
vy
vx
PID compensator
1.8
Vref
1/(2*pi*33e3)s+1
1/(2*pi*300e3)s+1
PD Compensator
1
Injection
point
1
1/(2*pi*1e6)s+1
HF pole
5.45
Gcm
1/(2*pi*8e3)s+1
1/(2*pi*8e3)s
Inverted zero
y
ECEN5807 35
Input and output linearization points for finding the loop-gain, T = -vy/vx
The output point (y) should be “Open Loop” , as shown by an x symbol next to the output arrow

36. Loop gain and stability margins
MATLAB script
BodePlotter_scriptT.m
(computes dc op,
linearizes calculates
linearizes, calculates
and plots frequency
response and stability
margins)
Bode Diagram
Gm Inf dB (at Inf Hz) Pm 51 6 deg (at 1 05e+005 Hz)
50
100
From: x To: Gcm/y
e
(dB)
Gm = Inf dB (at Inf Hz) , Pm = 51.6 deg (at 1.05e+005 Hz)
-100
-50
0
Magnitude
4
-135
-90
-45
Phase
(deg)
ECEN5807 36
10
2
10
3
10
4
10
5
10
6
10
7
-180
135
P
Frequency (Hz)

37. Closed-loop 0-5 Astep-load transient responses
Averaged model Switching model
v
i
vout
ig
5 s/div
5 s/div
ECEN5807 37
5 s/div
5 s/div
See MATLAB/Simulink page on the course website (“Materials” page)
for complete step-by-step details, and to download the example files