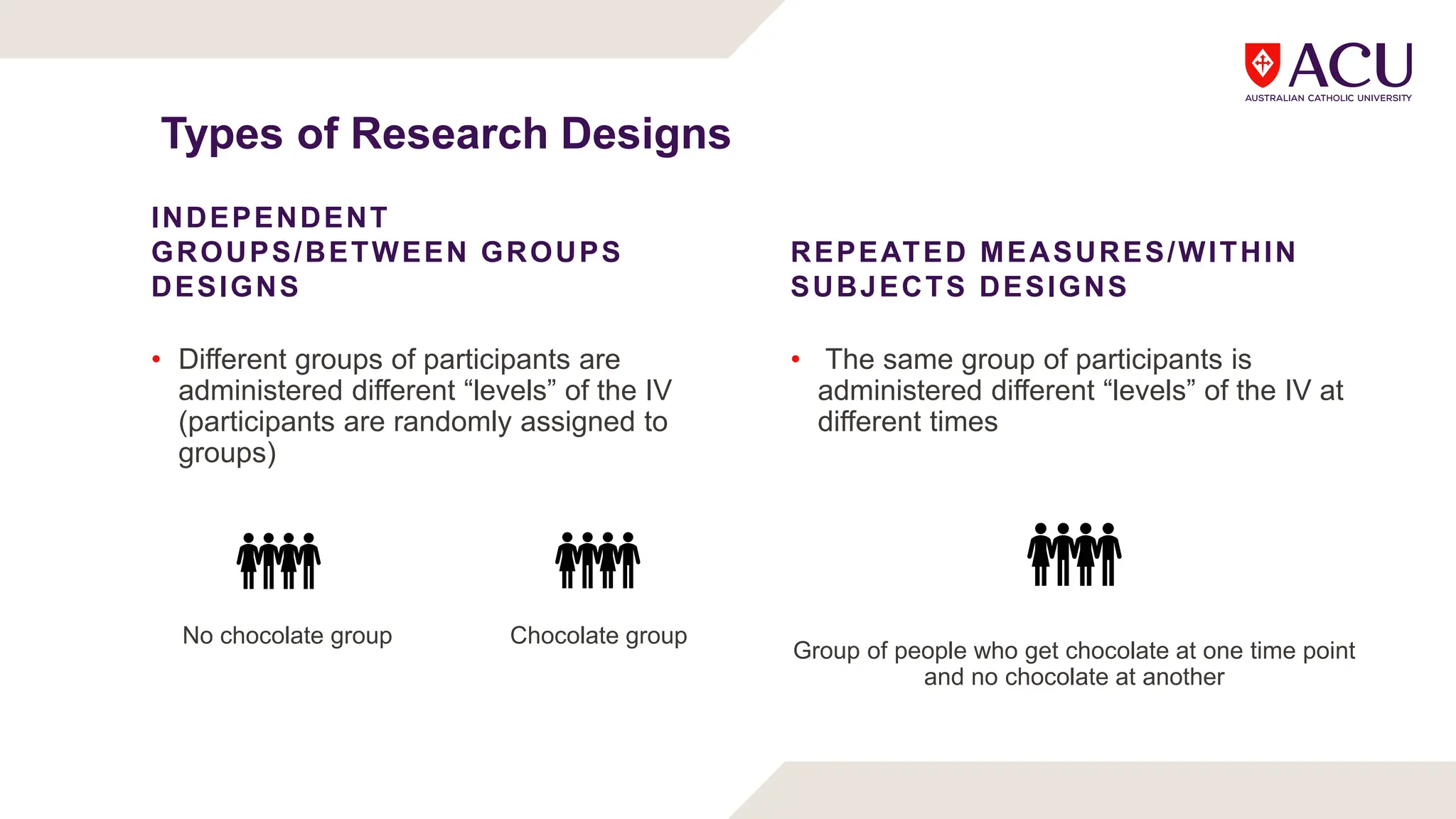
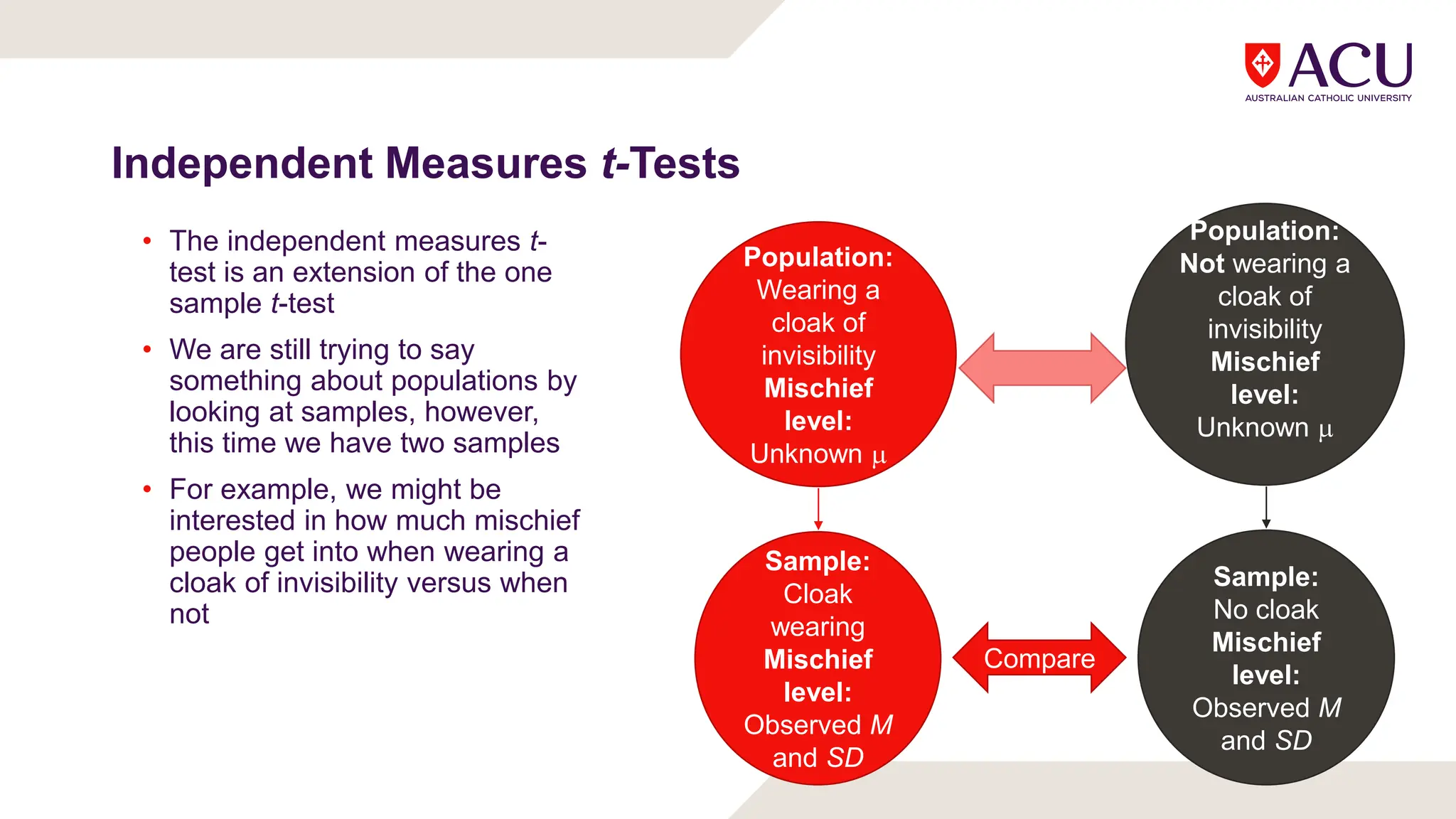
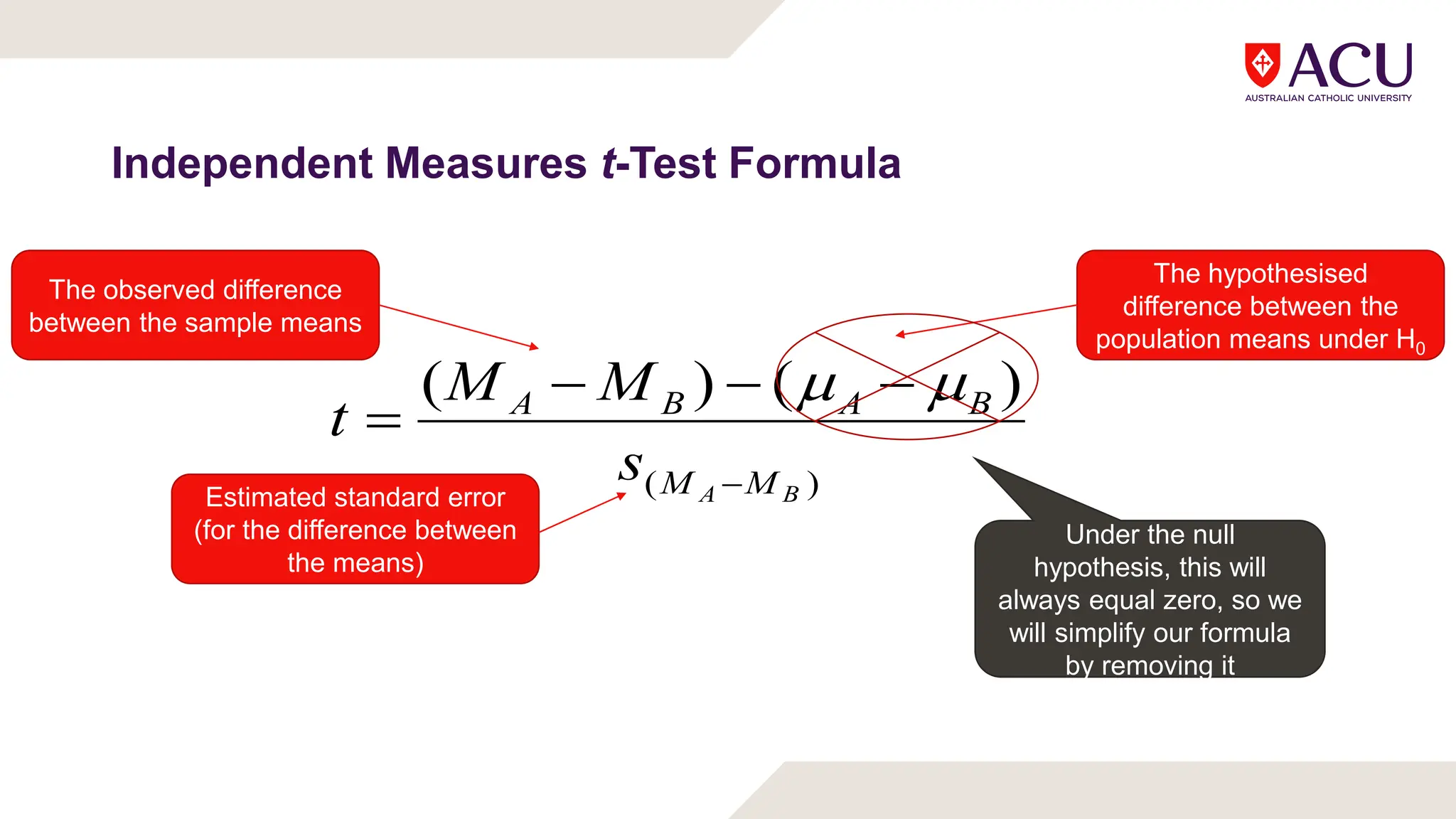
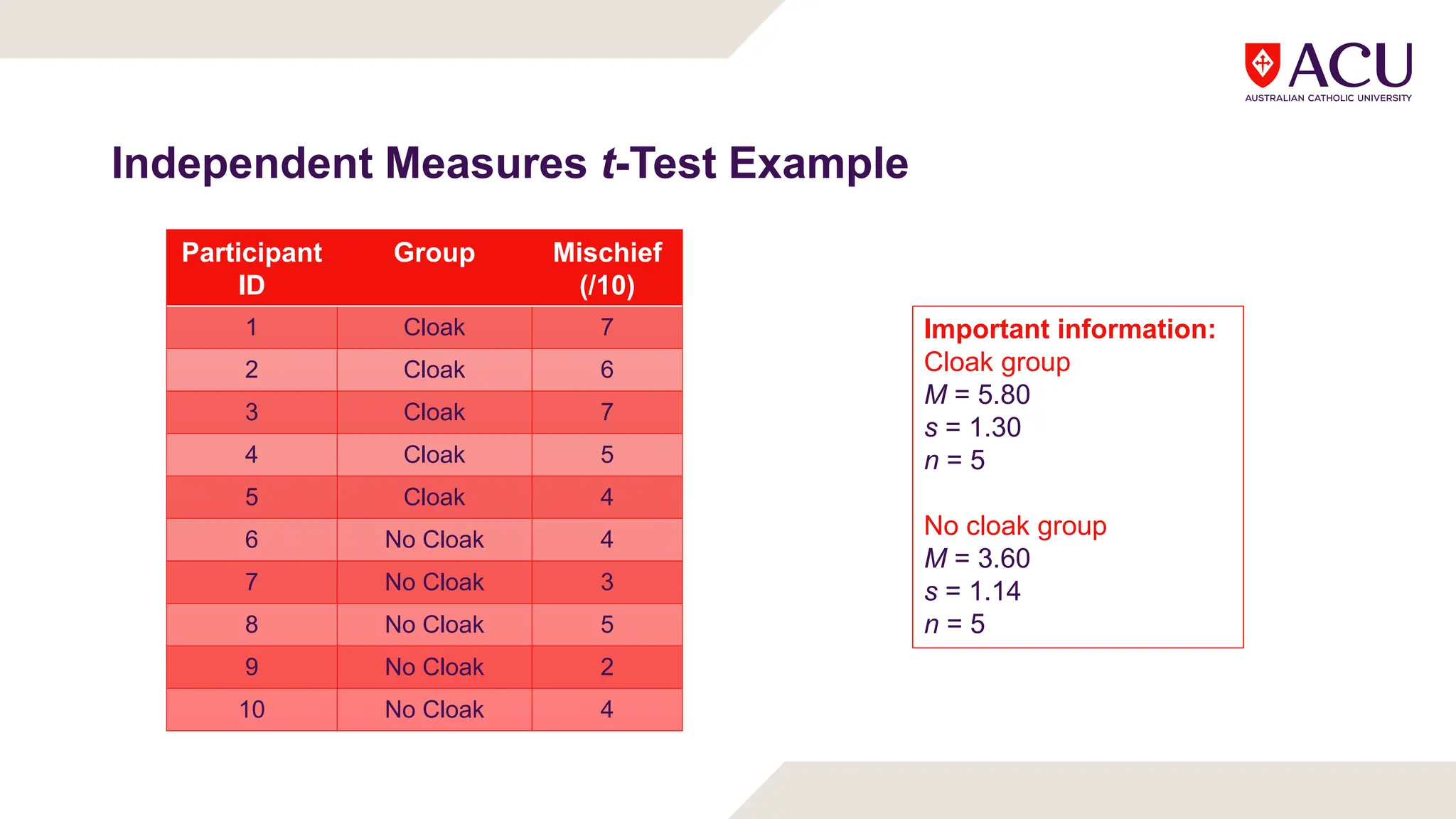
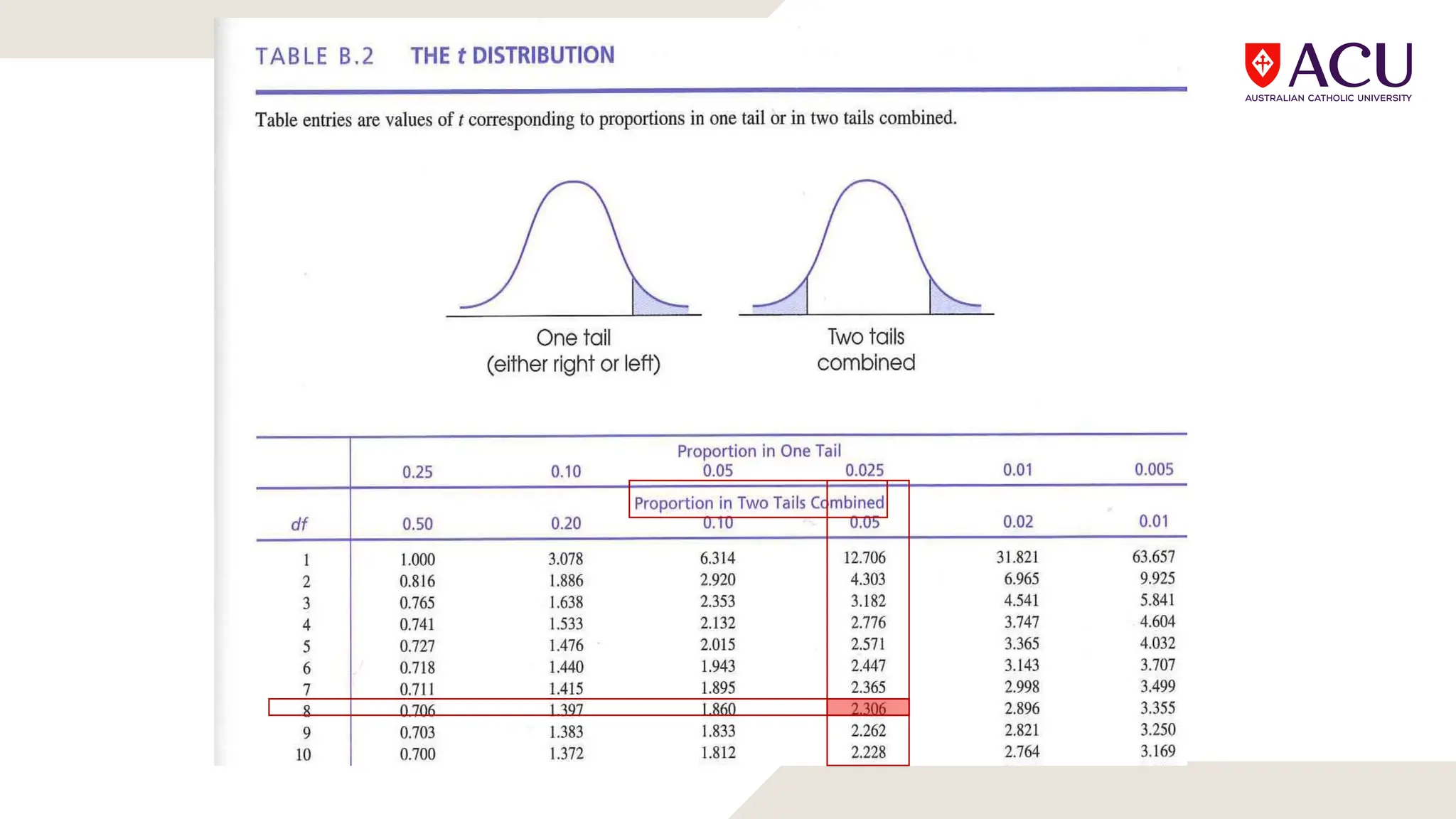
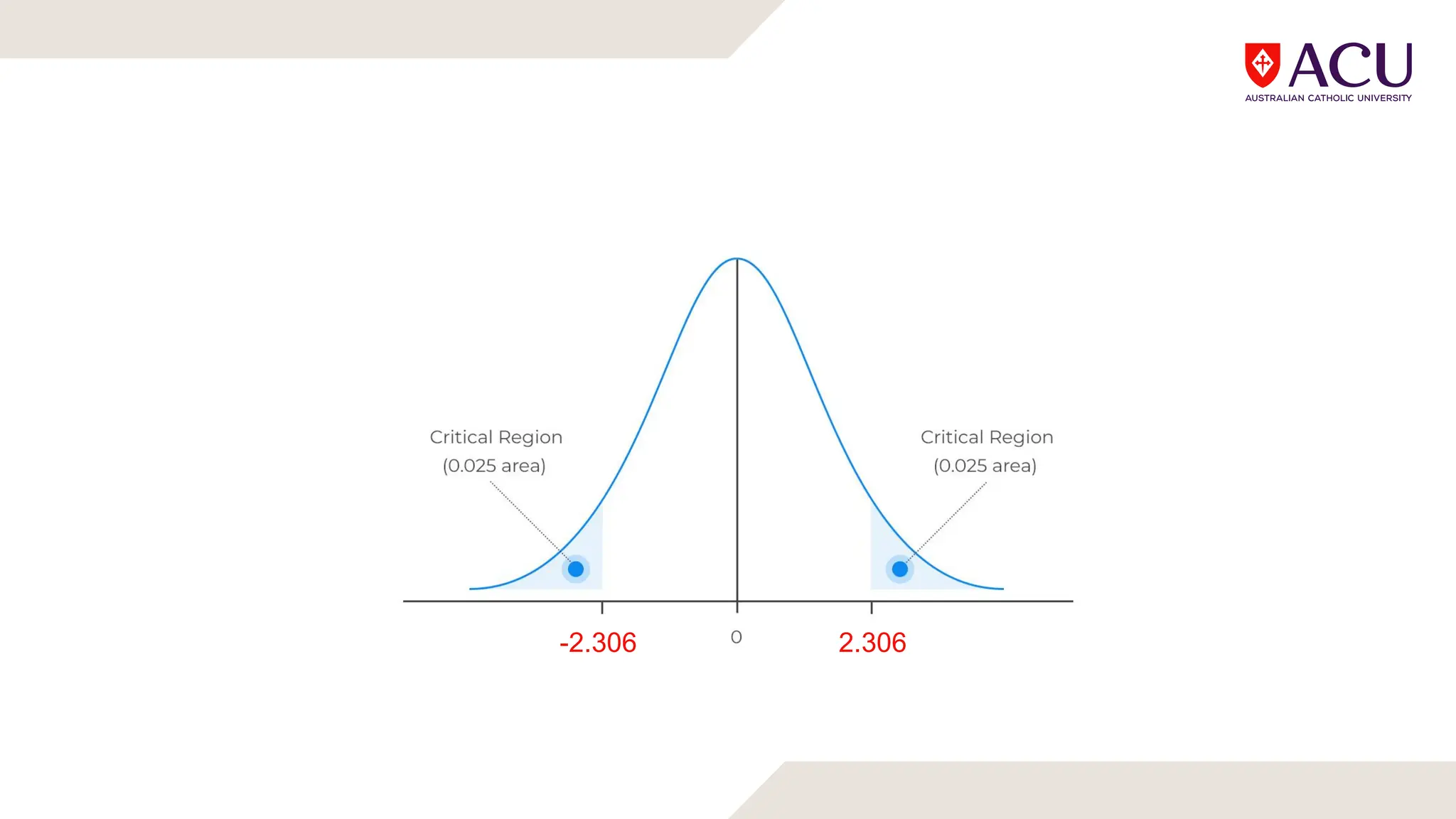
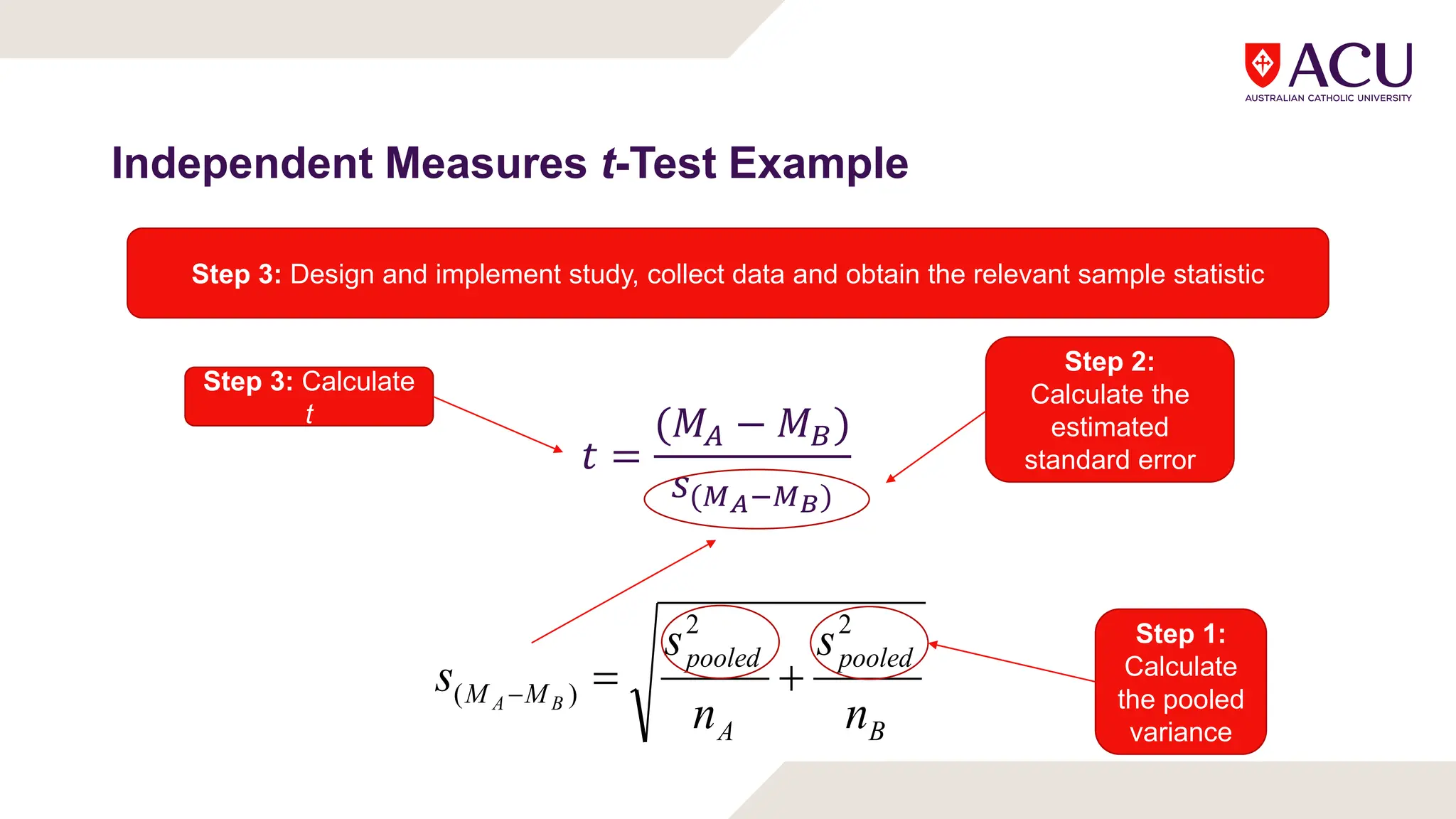
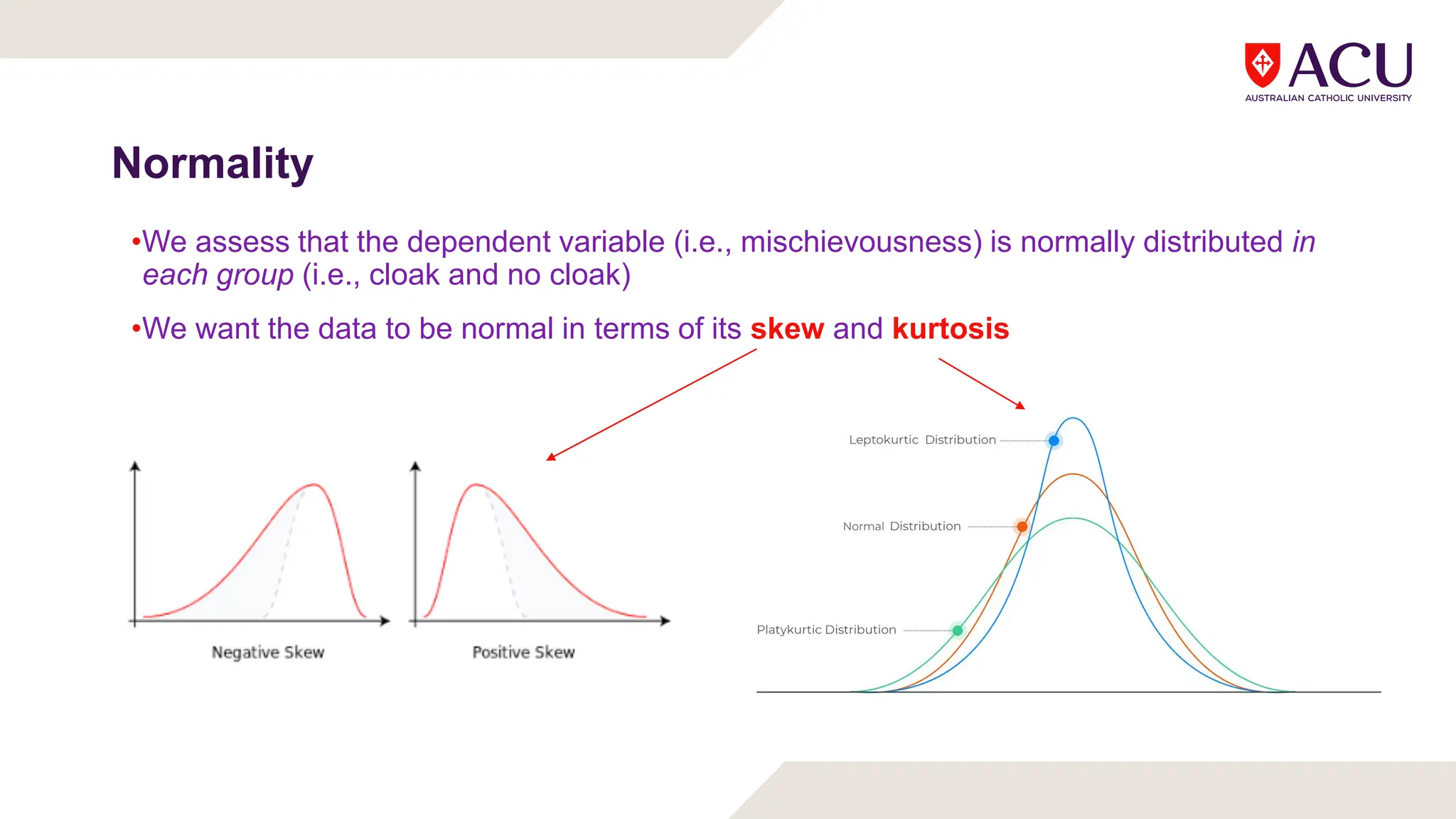
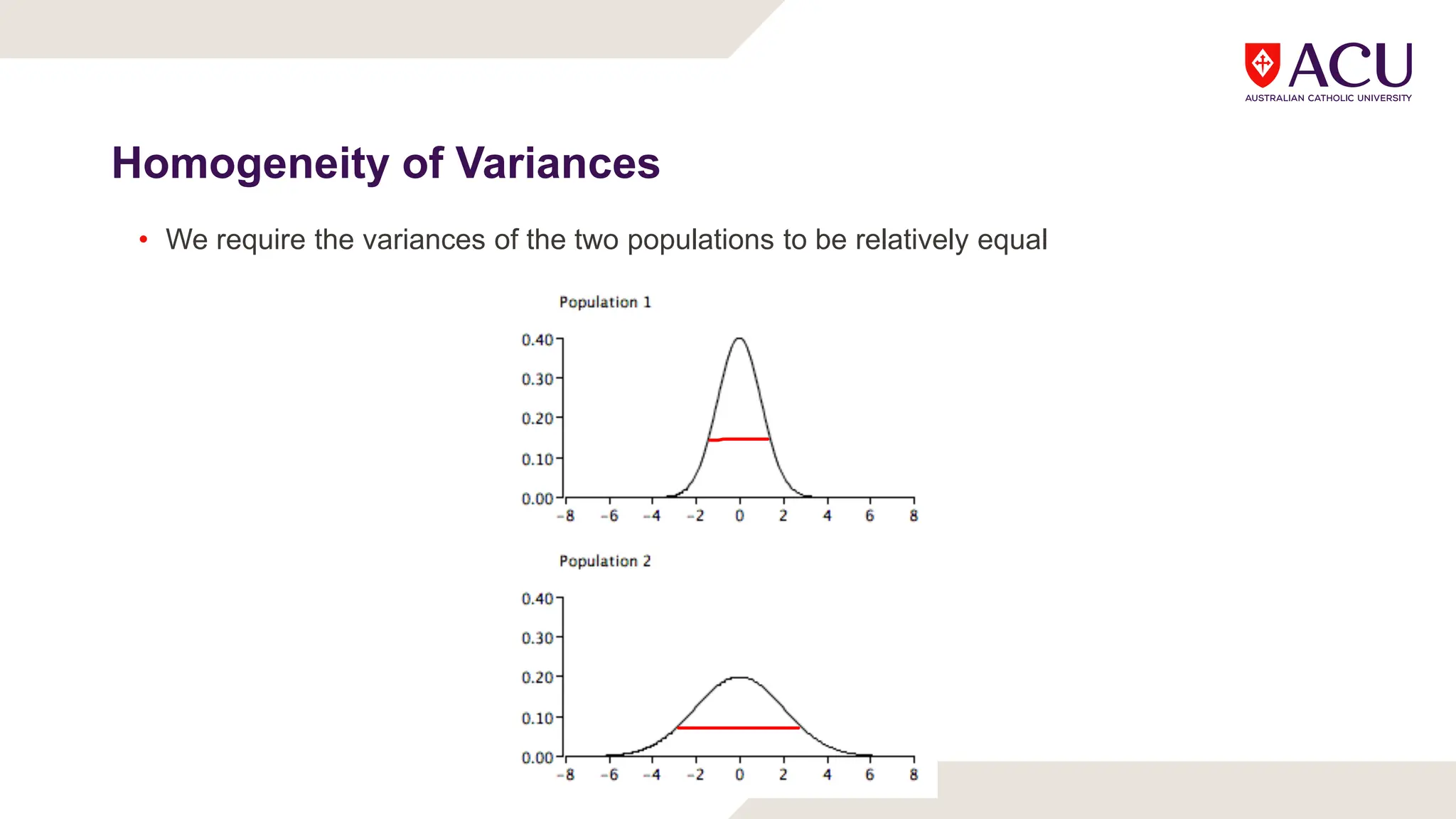
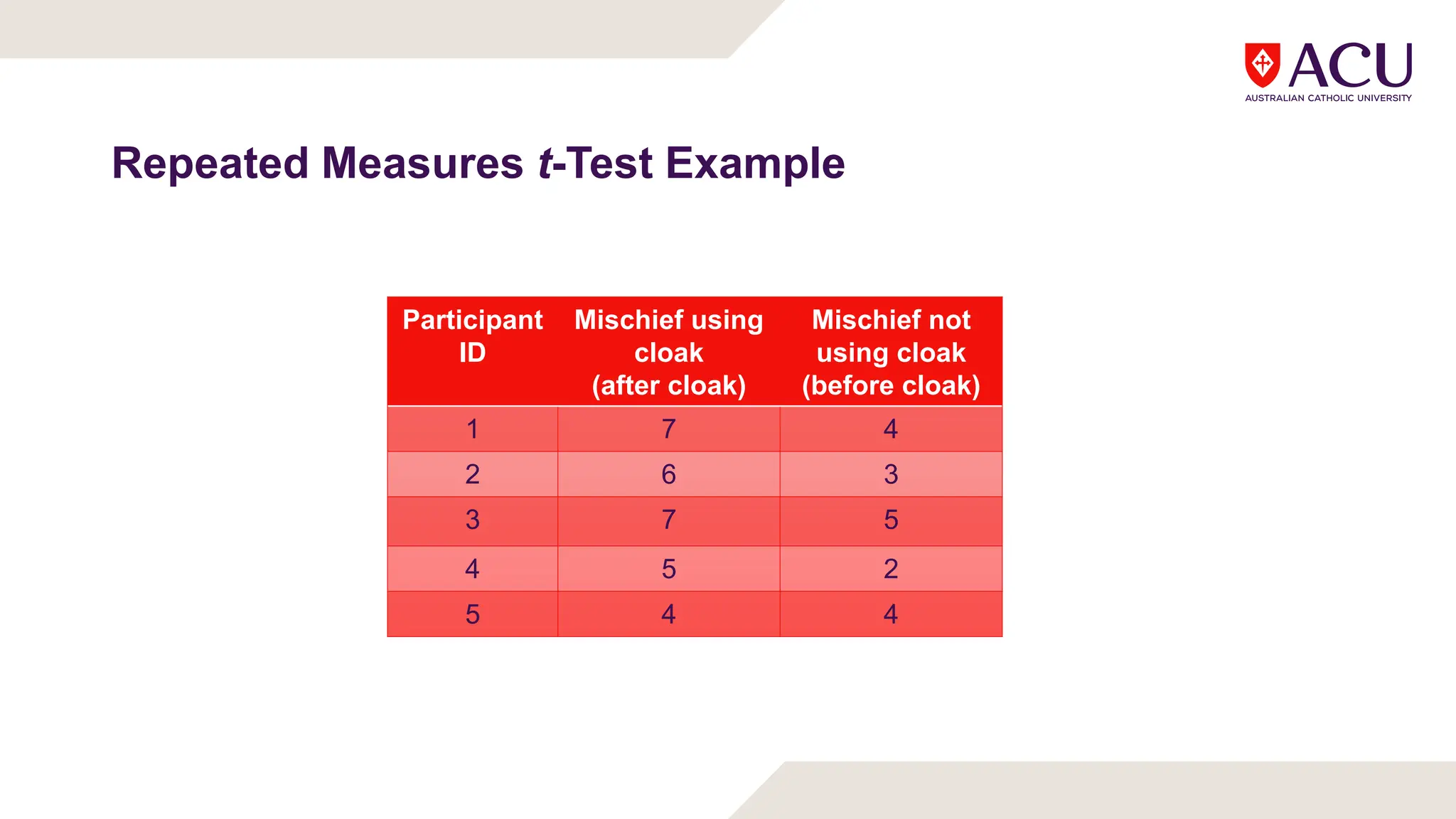
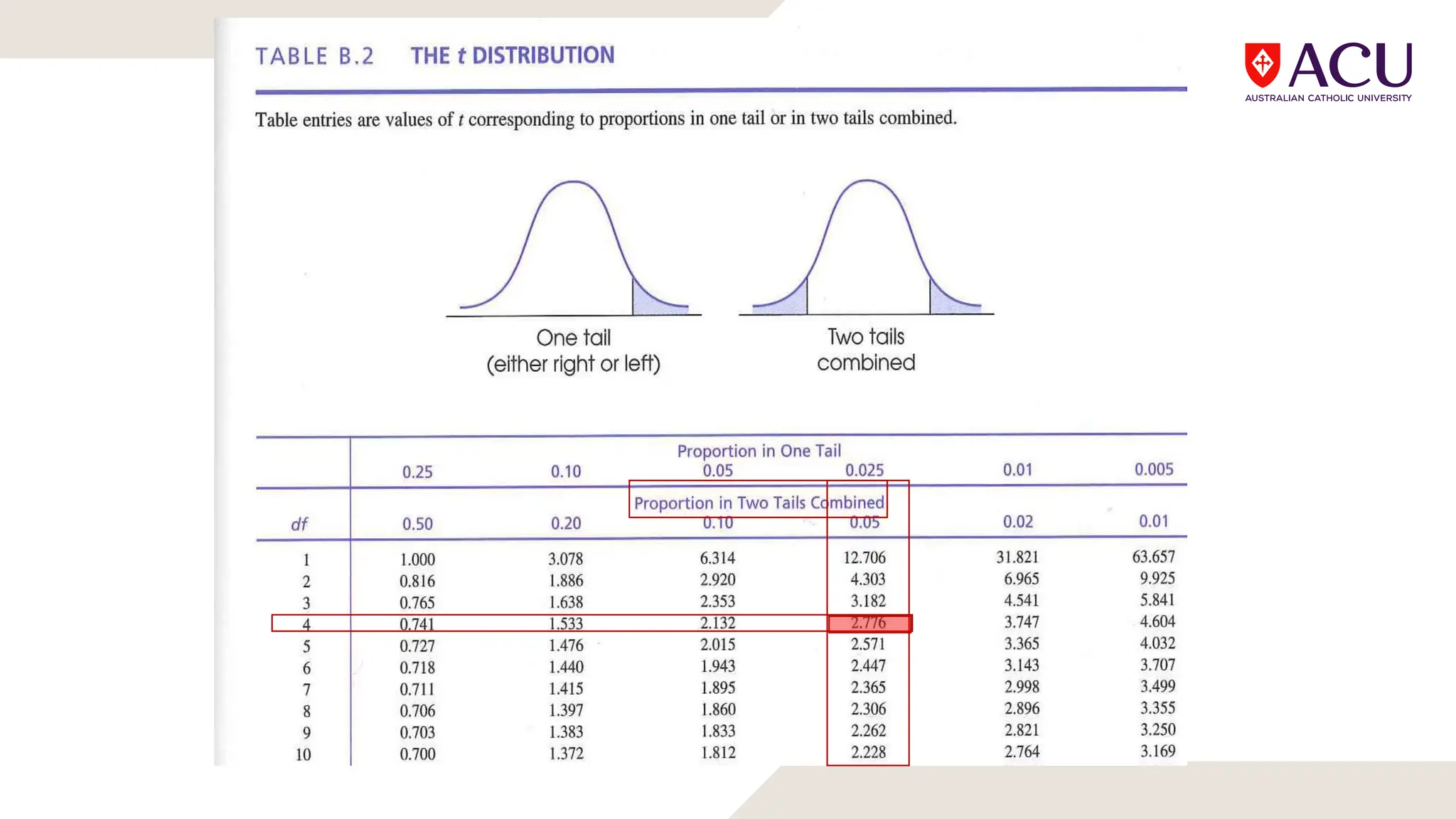
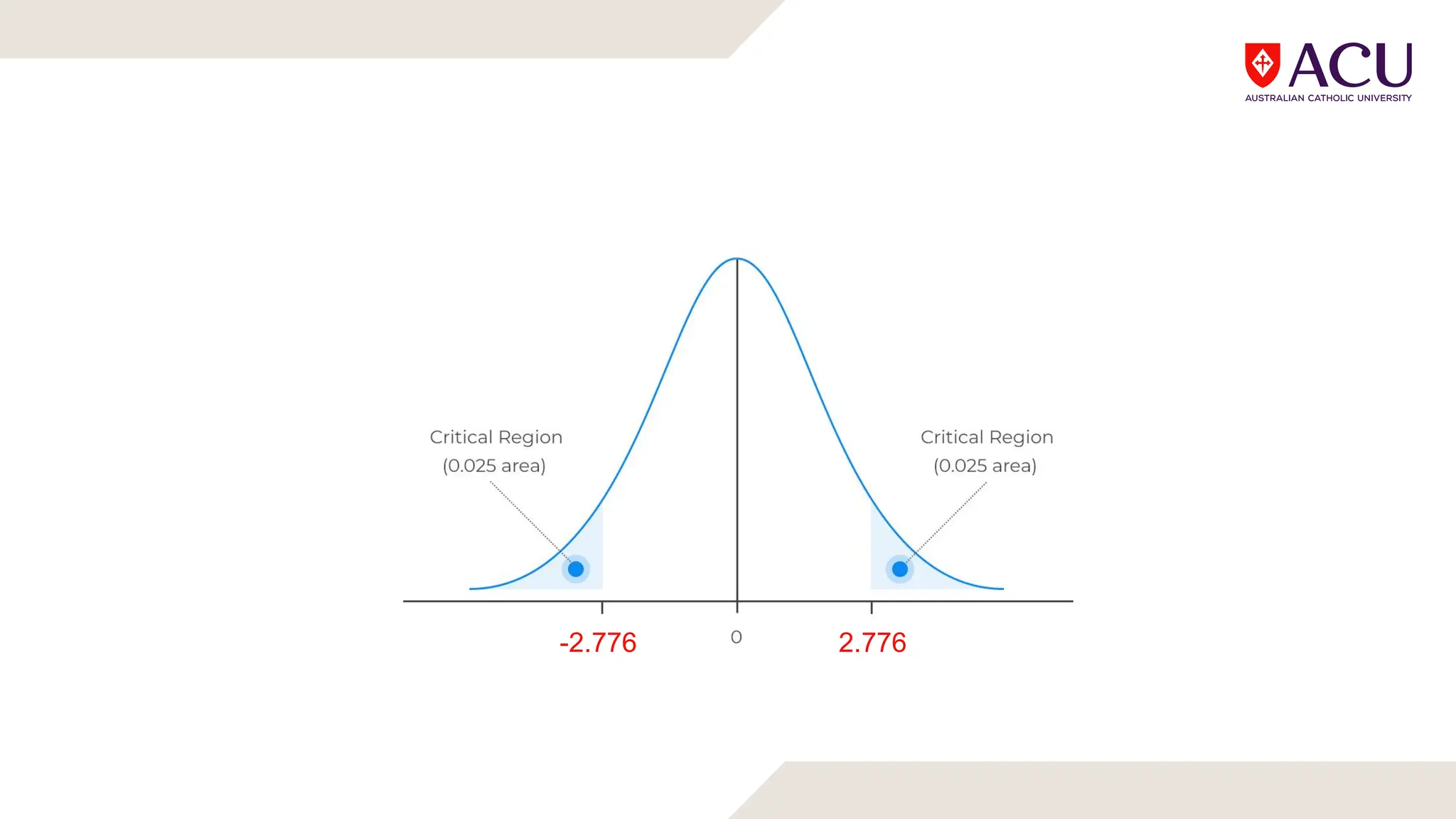
The document discusses three types of t-tests: one-sample, independent measures, and repeated measures t-tests, each used in different research scenarios. It outlines the research designs of repeated measures and independent groups, providing examples of their applications in psychological research. Additionally, it explains how to perform independent and repeated measures t-tests, including hypothesis generation, data collection, and statistical calculations.