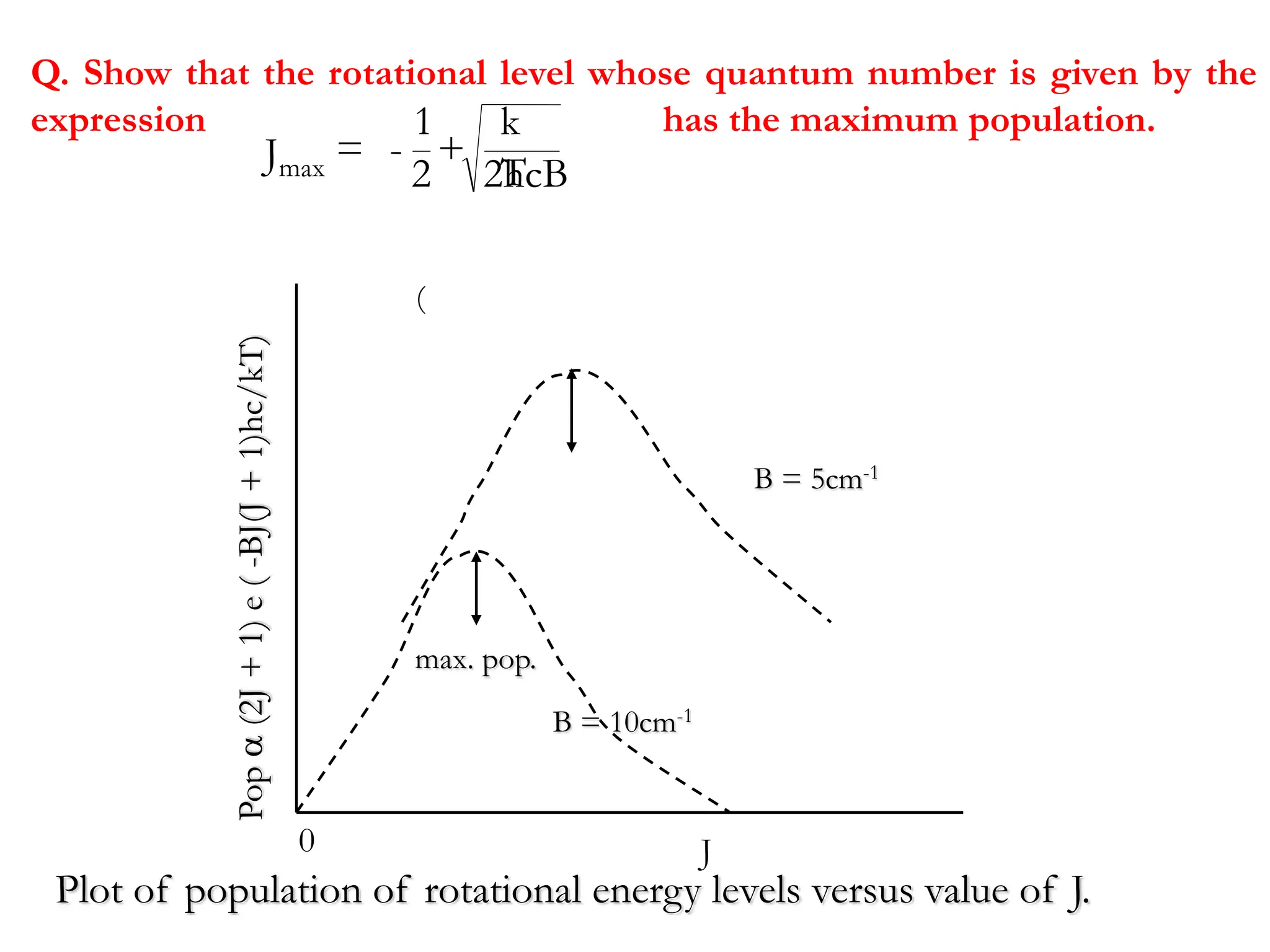
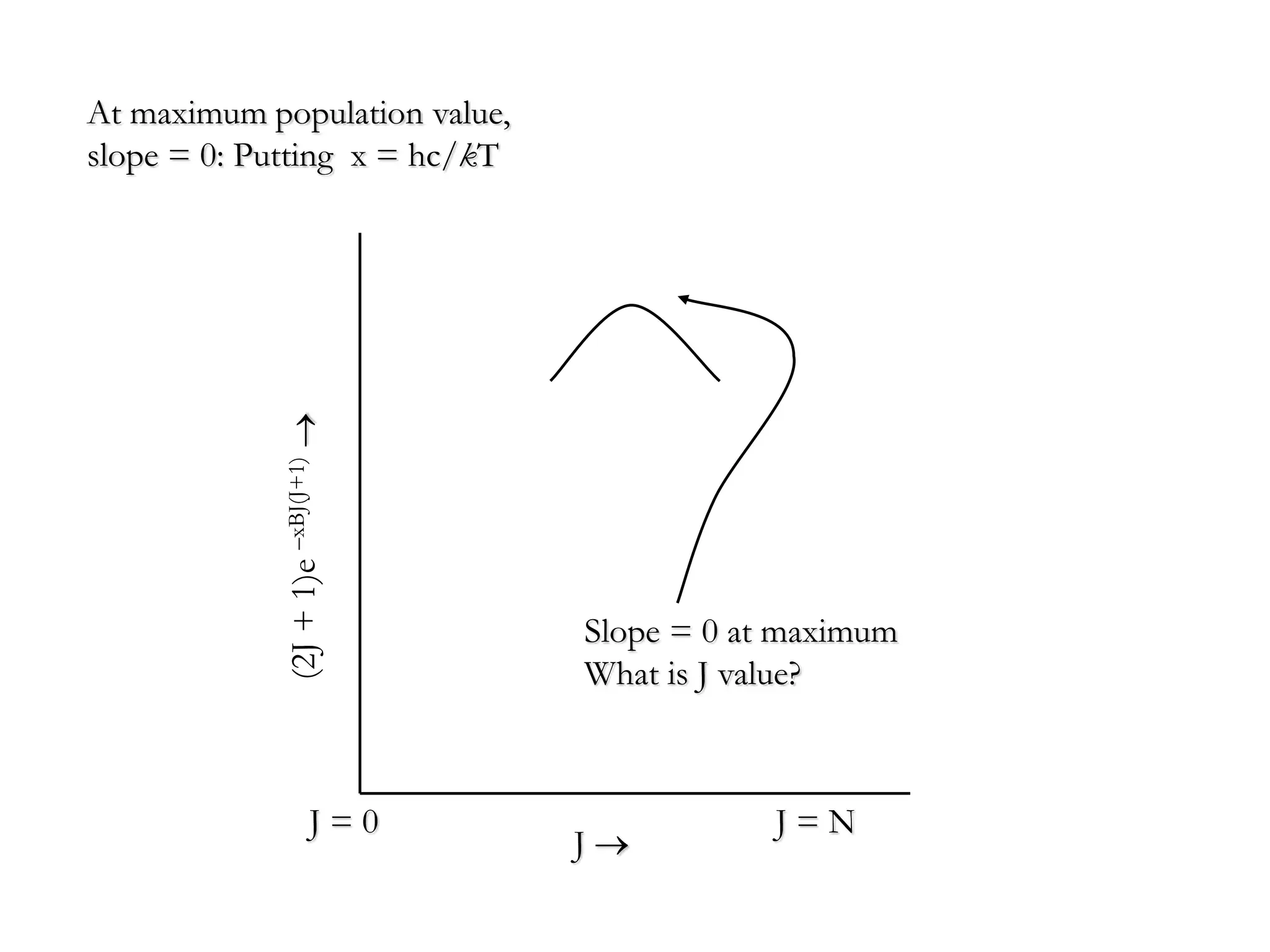
The document discusses the population of rotational energy levels in diatomic molecular gases, deriving expressions for maximum population and the conditions for equilibrium at temperature T. It also analyzes the molecular shapes of certain compounds and provides calculation details pertinent to bond lengths and vibrational transitions in harmonic oscillators. The allowed vibrational transitions based on selection rules are identified.

1. (
Plot of population of rotational energy levels versus value of J.
B = 5cm-1
B = 10cm-1
max. pop.
J
0
Pop

(2J
+
1)
e
(
-BJ(J
+
1)hc/kT)
Q. Show that the rotational level whose quantum number is given by the
expression has the maximum population.
2hcB
k
T
2
1
+
-
=
Jmax

2. At maximum population value,
slope = 0: Putting x = hc/kT
Slope = 0 at maximum
What is J value?
J = 0 J = N
J 
(2J
+
1)e
–xBJ(J+1)


3.  
 
   
 
2
1)
xB(2J
e
0
2e
1)
(2J
xBe
1)
(2J
0
0
e
1
2J
dJ
d
slope
2
1)
xBJ(J
1)
xBJ(J
1)
xBJ(J
1)
xBJ(J





















So:
2hcB
kT
2
1
2xB
1
2
1
Jmax
0
2
1)
xB(2J 2










Jmax
The derivative of a product of two
functions is equal to
the first times the derivative of
the second
plus the second times the
derivative of the first."

4. Show that the most populated rotational level in a diatomic
molecular gas at equilibrium at temperature T is given by:
b) d/dx(e−x.)= e−x (−1) = −e−x

5. Q.Indicate whether the following molecules are spherical,
symmetric, or asymmetric tops:
Sulphur trioxide, methane, sulphur tetrafluoride, sulphur
hexafluoride, nitrogen trifluoride, ethylene, ethane, benzene,
allene.

9. Answer:
1
-
4
3
3
cm
2
.
2995
10
3
.
5
)
593
.
10
(
4
4






D
B
ω

10. . Calculate the bond length of using and the reduced mass is .

11. Vibrating Diatomic Molecules
4. Which of the following vibrational transitions will be observed for a
diatomic molecule (treated as a harmonic oscillator): v = 1 to v = 3; v =
2 to v = 3; v = 5 to v = 4.
Answer:
The selection rules for vibrational translations is . Therefore, the
allowed transitions are v = 2 to v = 3; and v = 5 to v = 4.