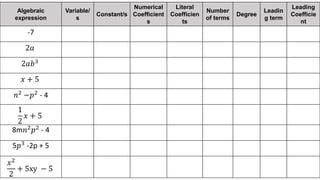
The document discusses the key terms and concepts related to algebra. It begins by explaining that Al-Khwarizmi is considered the father of algebra and the origin of the word "algebra" comes from the title of one of his books. It then defines important terms in algebra like variables, constants, terms, algebraic expressions, degree of a polynomial, leading term, and leading coefficient. Finally, it covers the four basic operations that can be performed on polynomials - addition, subtraction, multiplication, and division - and provides examples of how to apply rules and properties like the distributive property and laws of exponents when operating on polynomials.