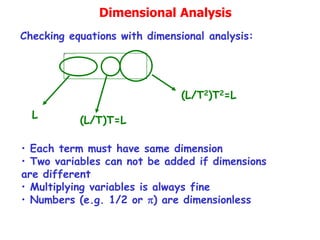
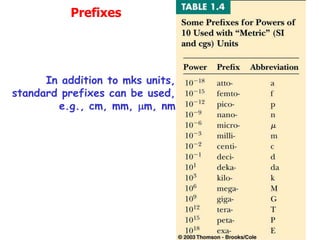
The document provides an overview of the Introductory Physics I course (Physics 231) at Michigan State University, focusing on topics such as mechanics, thermodynamics, and waves. It emphasizes the importance of doing homework, utilizing help resources, and understanding concepts deeply. Additionally, it covers fundamental units and dimensions, dimensional analysis, and the validity of equations in physics.

1. PHYSICS 231
INTRODUCTORY PHYSICS I
www.pa.msu.edu/courses/phy231
Scott Pratt
prattsc@msu.edu
(517) 355-9200, ext. 2016
Office Hours:
Monday, 9-10:30 AM in 1248 BPS

2. Course Information
http://www.pa.msu.edu/courses/phy231

3. Succeeding in Physics 231
1) Do your homework (yourself)!
2) Use the help room (1248 BPS) !
3) Make sure you understand both “why” and “why
not”
4) Interrupt the lecturer!

4. General Physics
• First Semester (Phy 231)
• Mechanics
• Thermodynamics
• Simple harmonic motion
• Waves
Second Semester (Phy 232)
• Electromagnetism
• Relativity
• Modern Physics
• (Quantum Mechanics, …, etc.)

5. Mechanics
• Half the course
• Quantified largely by Galileo
• Problems involve:
velocity, acceleration, mass, momentum, energy,
torque, angular momentum, moment of inertia…

6. UNITS (Systéme Internationale)
Dimension SI (mks) Unit Definition
Length meters (m) Distance traveled by light in
1/(299,792,458) s
Mass kilogram (kg) Mass of a specific platinum-
iridium allow cylinder kept by
Intl. Bureau of Weights and
Measures at Sèvres, France
Time seconds (s) 9,192,631,700 oscillations of
cesium atom

7. Standard Kilogram
at Sèvres

8. Dimensional Analysis
Dimensions & units can be treated algebraically.
Variable from Eq. x m t v=(xf-xi)/t a=(vf-vi)/t
dimension L M T L/T L/T2

9. Dimensional Analysis
Checking equations with dimensional analysis:
L
(L/T)T=L
(L/T2)T2=L
• Each term must have same dimension
• Two variables can not be added if dimensions
are different
• Multiplying variables is always fine
• Numbers (e.g. 1/2 or p) are dimensionless

10. Example 1.1
Check the equation for dimensional consistency:
2
2
2
)
/
(
1
mc
c
v
mc
mgh 


Here, m is a mass, g is an acceleration,
c is a velocity, h is a length

11. Example 1.2
L3/(MT2)
Consider the equation:
Where m and M are masses, r is a radius and
v is a velocity.
What are the dimensions of G ?

12. Example 1.3
Given “x” has dimensions of distance, “u” has
dimensions of velocity, “m” has dimensions of
mass and “g” has dimensions of acceleration.
Is this equation dimensionally valid?
Yes
Is this equation dimensionally valid?
No

13. Units vs. Dimensions
• Dimensions: L, T, M, L/T …
• Units: m, mm, cm, kg, g, mg, s, hr, years …
• When equation is all algebra: check dimensions
• When numbers are inserted: check units
• Units obey same rules as dimensions:
Never add terms with different units
• Angles are dimensionless but have units
(degrees or radians)
• In physics sin(Y) or cos(Y) never occur unless Y
is dimensionless

14. Example 1.3
Grandma traveled 27 minutes at 44 m/s.
How many miles did Grandma travel?
44.3 miles

15. Prefixes
In addition to mks units,
standard prefixes can be used,
e.g., cm, mm, mm, nm

16. Example 1.4a
The above expression yields:
a) 40.11 m
b) 4011 cm
c) A or B
d) Impossible to evaluate (dimensionally invalid)

17. Example 1.4b
The above expression yields:
a) 4.5 m kg
b) 4.5 g km
c) A or B
d) Impossible to evaluate (dimensionally invalid)

18. Example 1.4b
The above expression yields:
a) -1.5 m
b) -1.5 kg m2
c) -1.5 kg
d) Impossible to evaluate (dimensionally invalid)