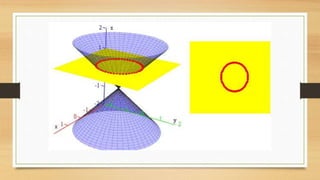
The document discusses conic sections and circles. It defines conic sections as curves formed by the intersection of a plane and a double cone. The four types of conic sections are circles, ellipses, parabolas, and hyperbolas. It then defines a circle and provides the standard form equation of a circle. Examples are given to determine the type of conic section for different quadratic equations by calculating the discriminant.