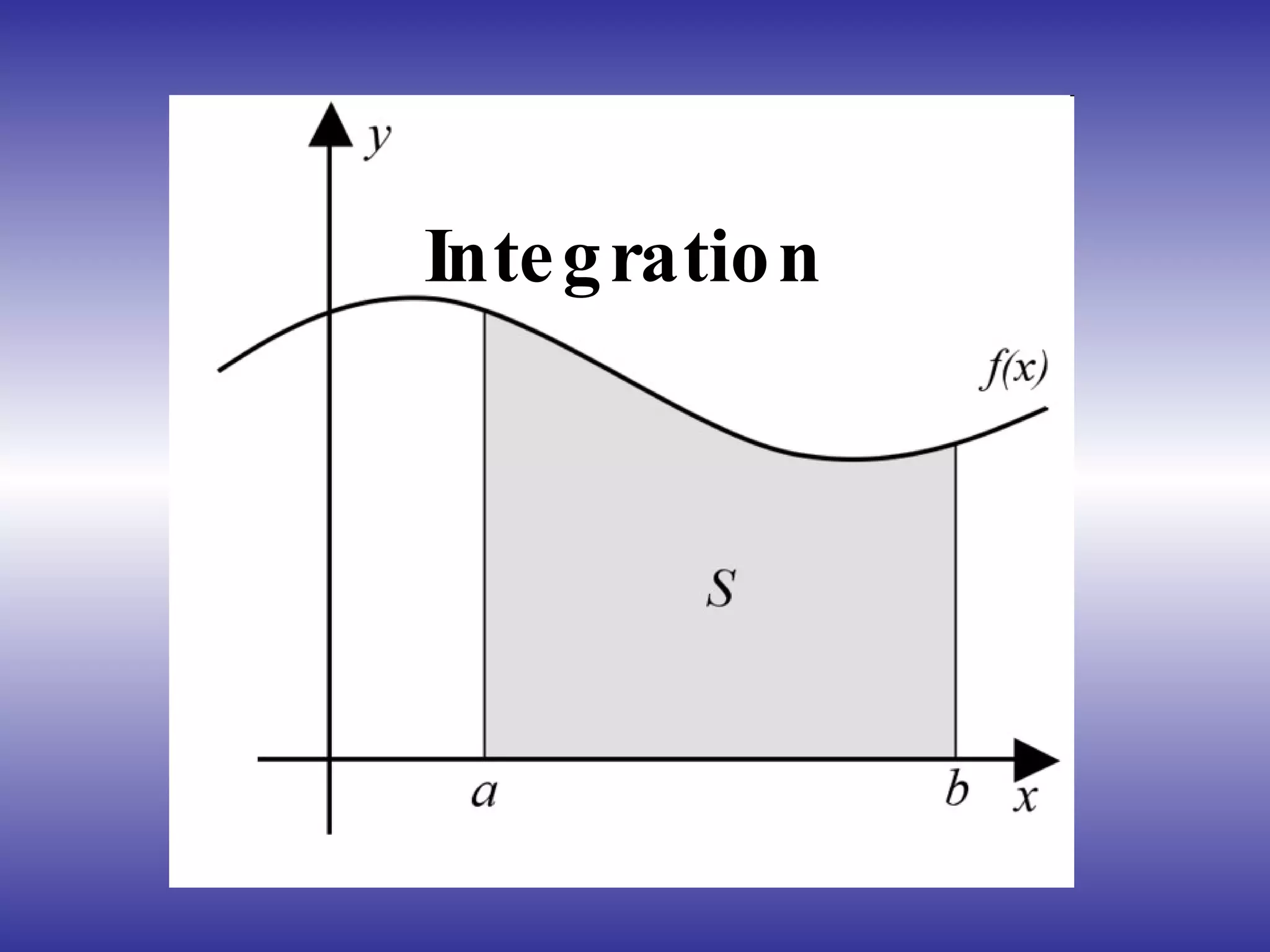
Integrals are used to find the area or volume bounded by lines and can be definite or indefinite. There are several methods for solving integrals including the reverse power rule, substitution method, and evaluating definite integrals by substituting the bounds. Indefinite integrals are anti-derivatives with an added constant, while definite integrals substitute bounds to find the area between them. Position, velocity and acceleration are related through integrals as well.

1. Integration

2. INTEGRAL

3. An integral is used to find the area or volume bounded by a line or lines Can be definite or indefinite Definition

4. Reverse Power Rule

5. Used to solve integrals Add one to the exponent Divide coefficient by new exponent

6. Substitution Method

7. Used for functions with: Quantity raised to a power Trig function with unusual angle Trig function raised to a power

8. Determine which quantity can be manipulated and include the entire problem Set that equal to U and take the derivative Manipulate the derivative to equal the original integral Take the anti-derivative of U and its new parts Substitute the original function that was equal to U Add C and set the function equal to F(x)

9. Trig with Unusual Angle Quantity Raised to a Power

10. Definite Integrals

11. Integrals with bounds To solve these, take the integral and then substitute the bounds in for x. Subtract the value found from the bottom bound from the top bottom value

12. Indefinite Integrals

13. Integrals without bounds Take the anti-derivative of the integral Add C and set this equal to F(x)

14. Position, Velocity, and Acceleration

15. Anti-derivative of Acceleration is Velocity Anti-derivative of Velocity is Position Remember to use a constant when finding original position function

16. INTEGRALS ARE FUN!!!