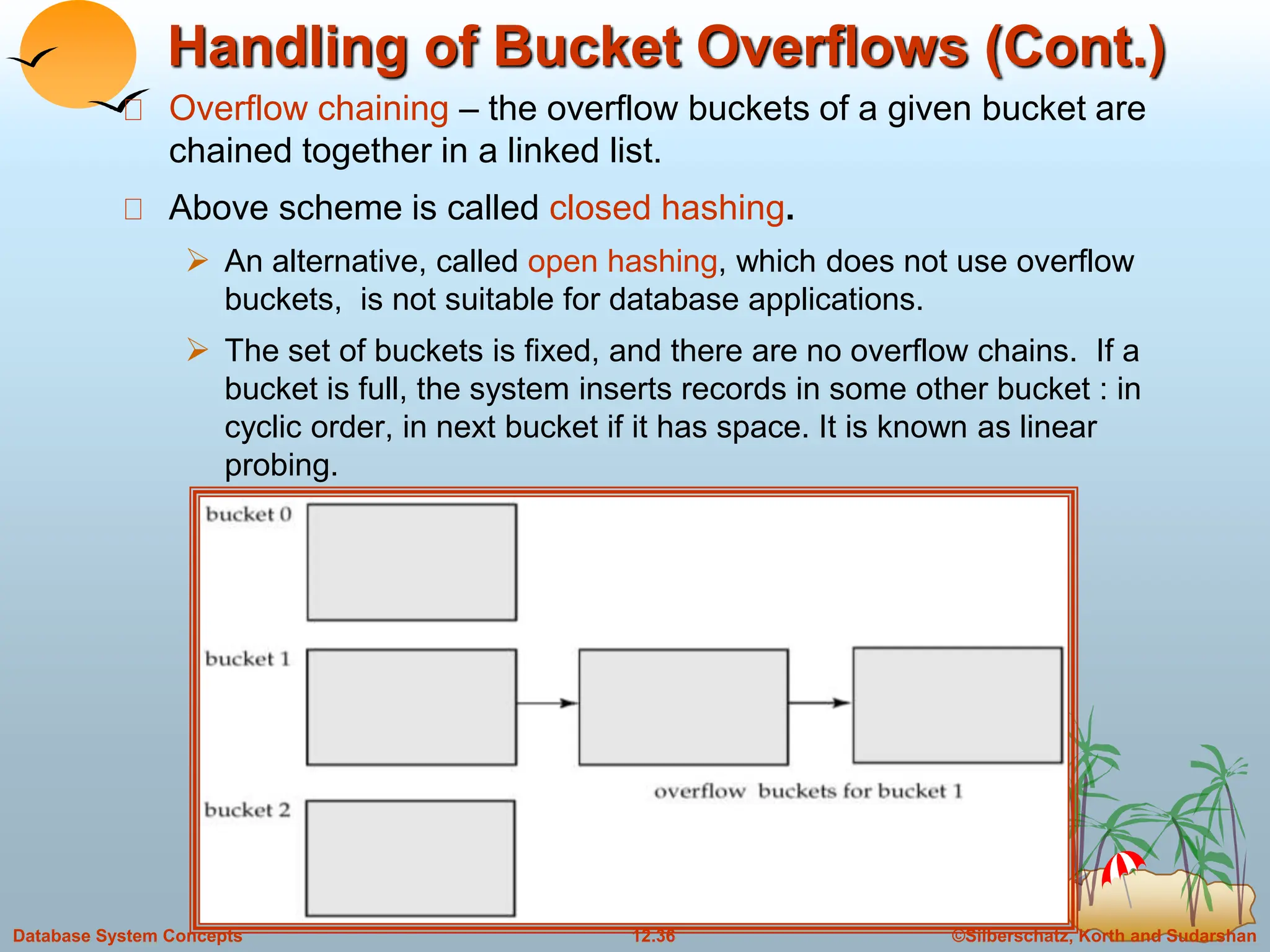
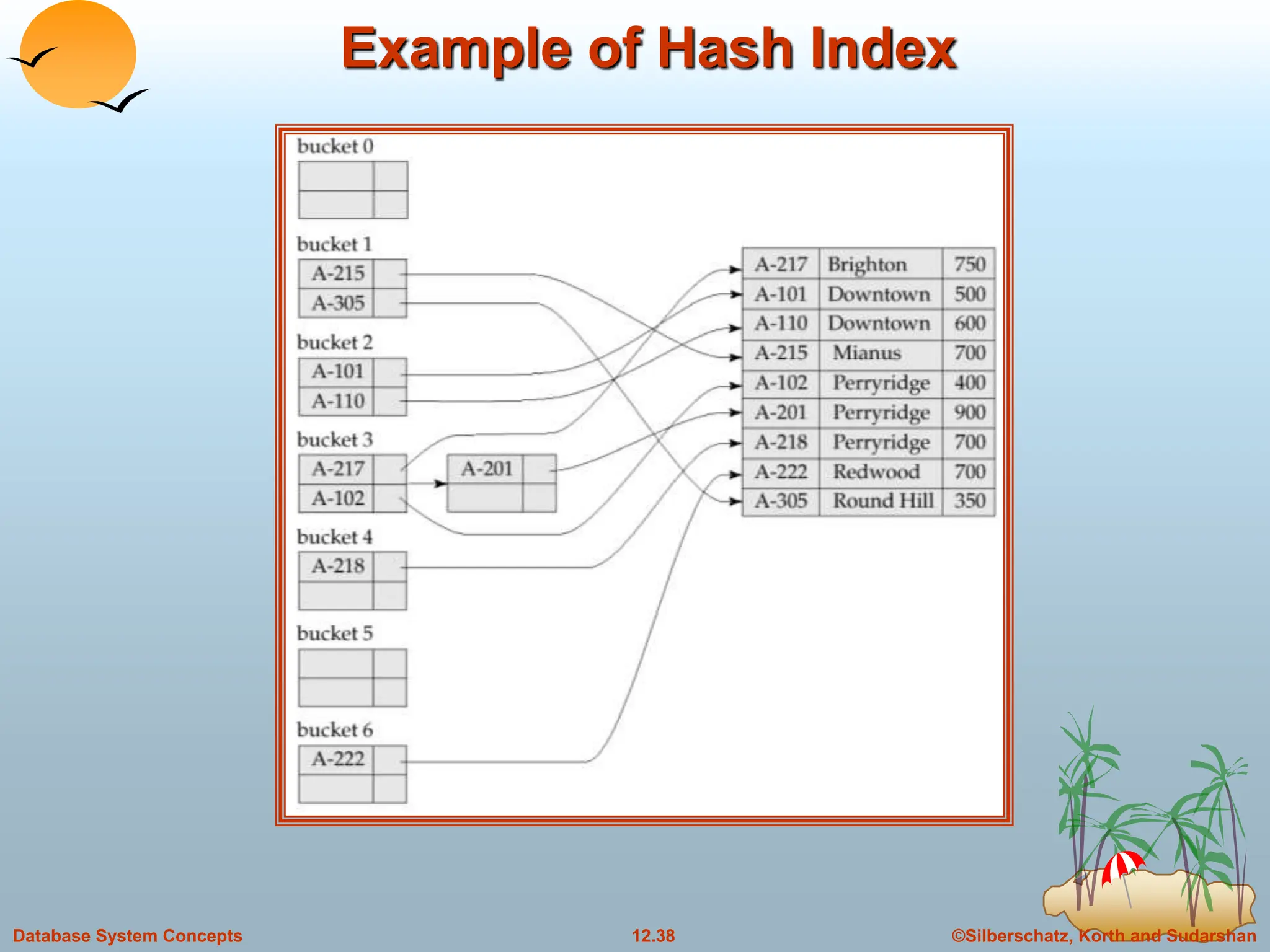
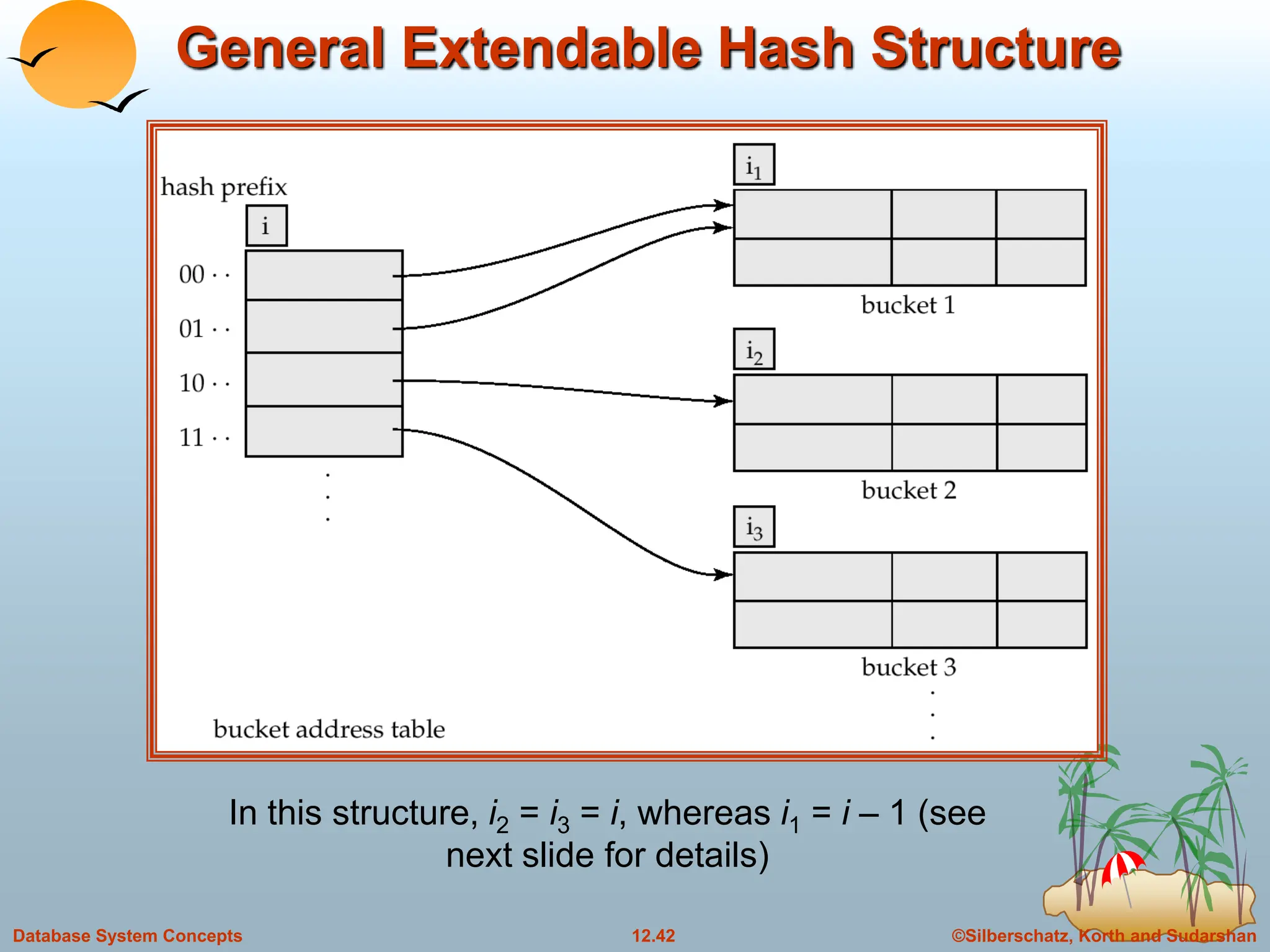
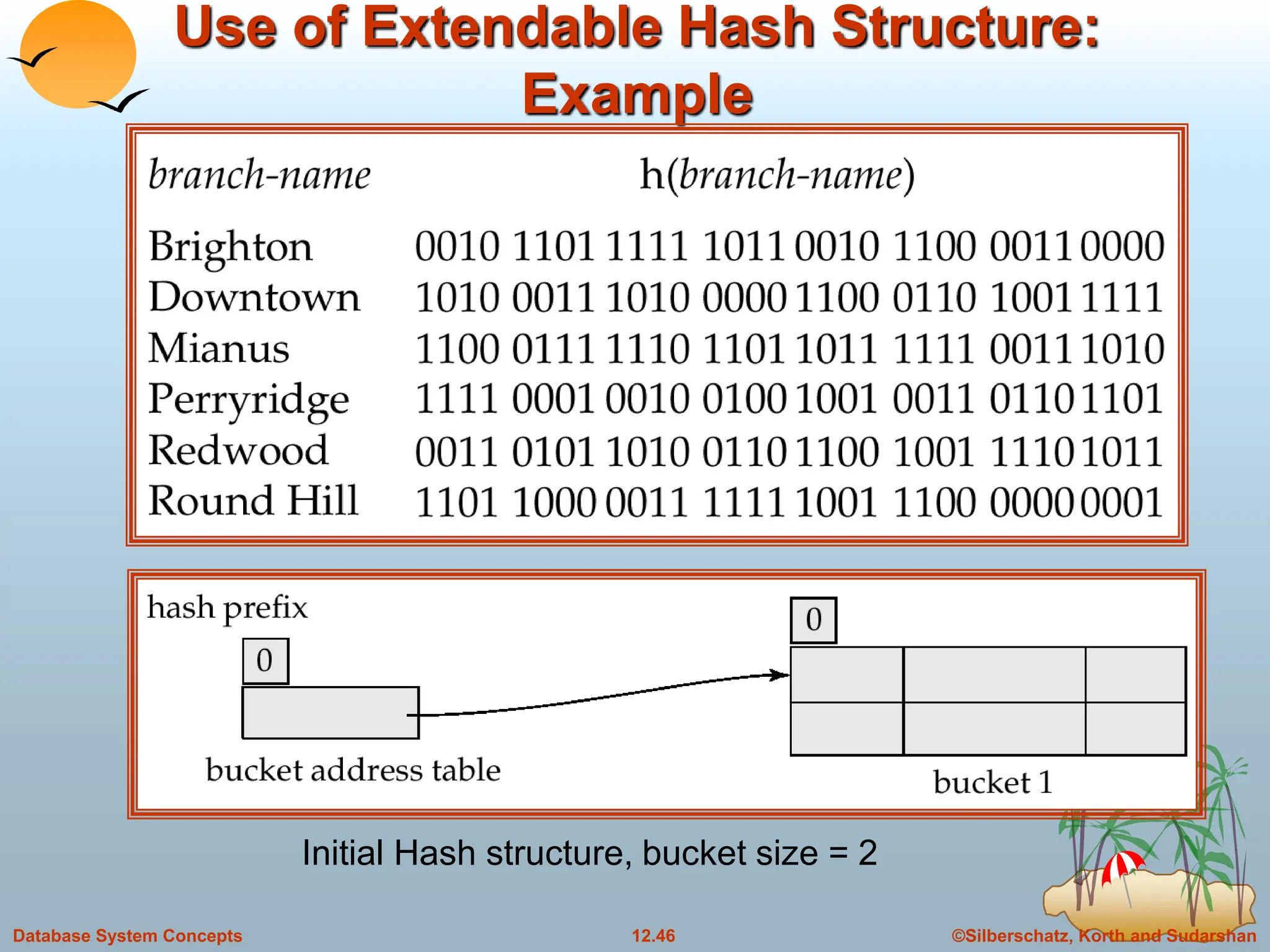
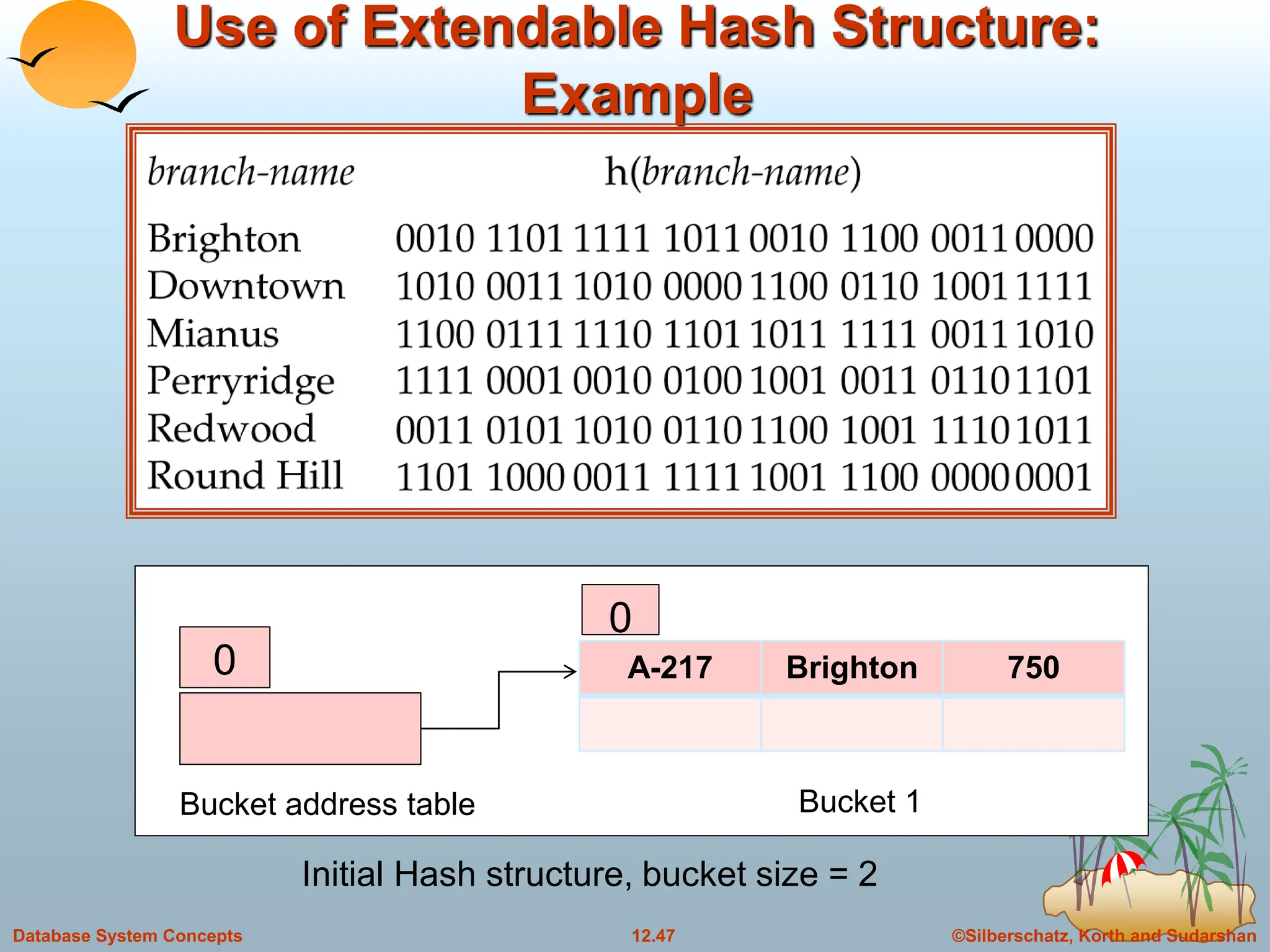
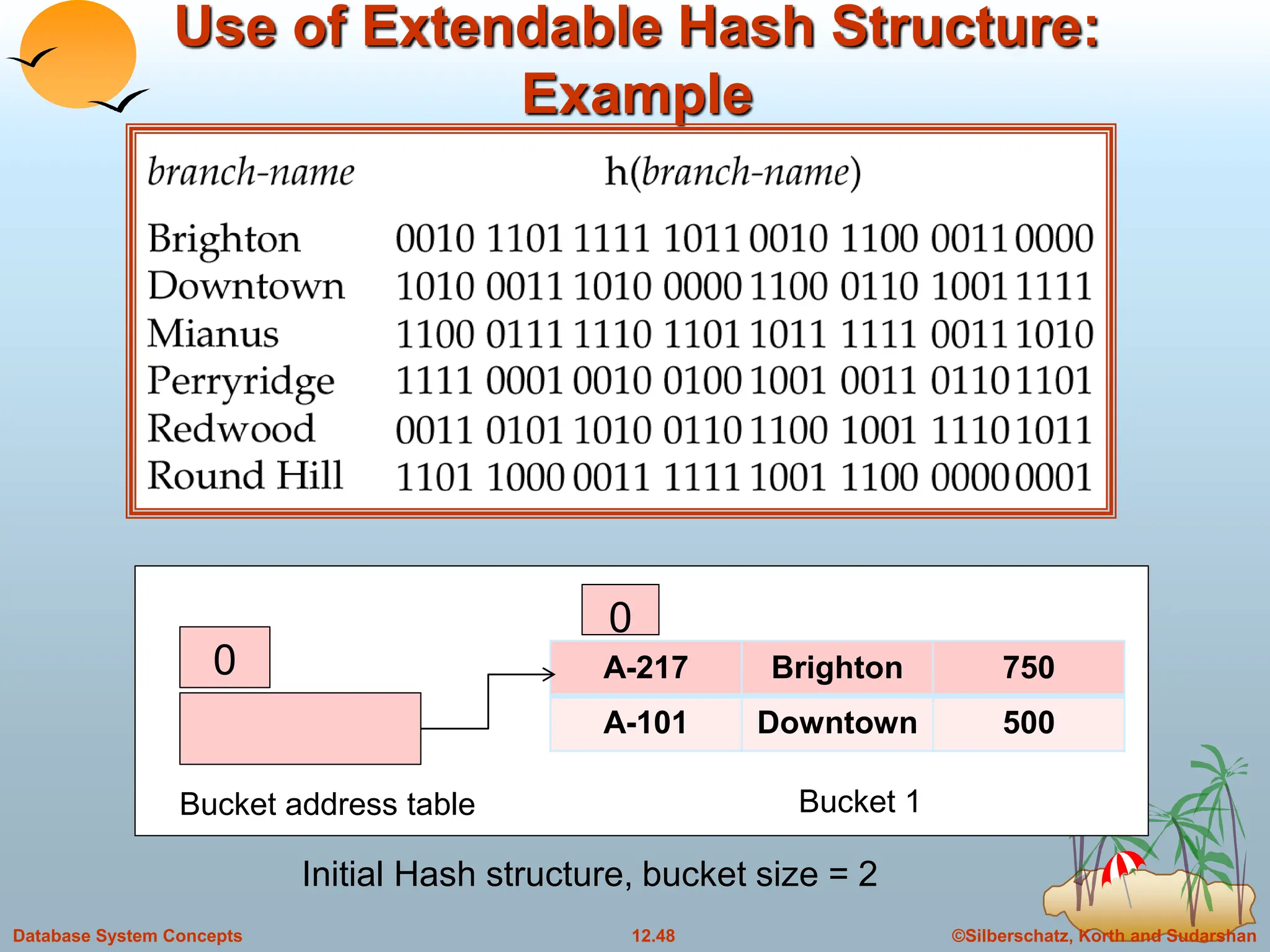
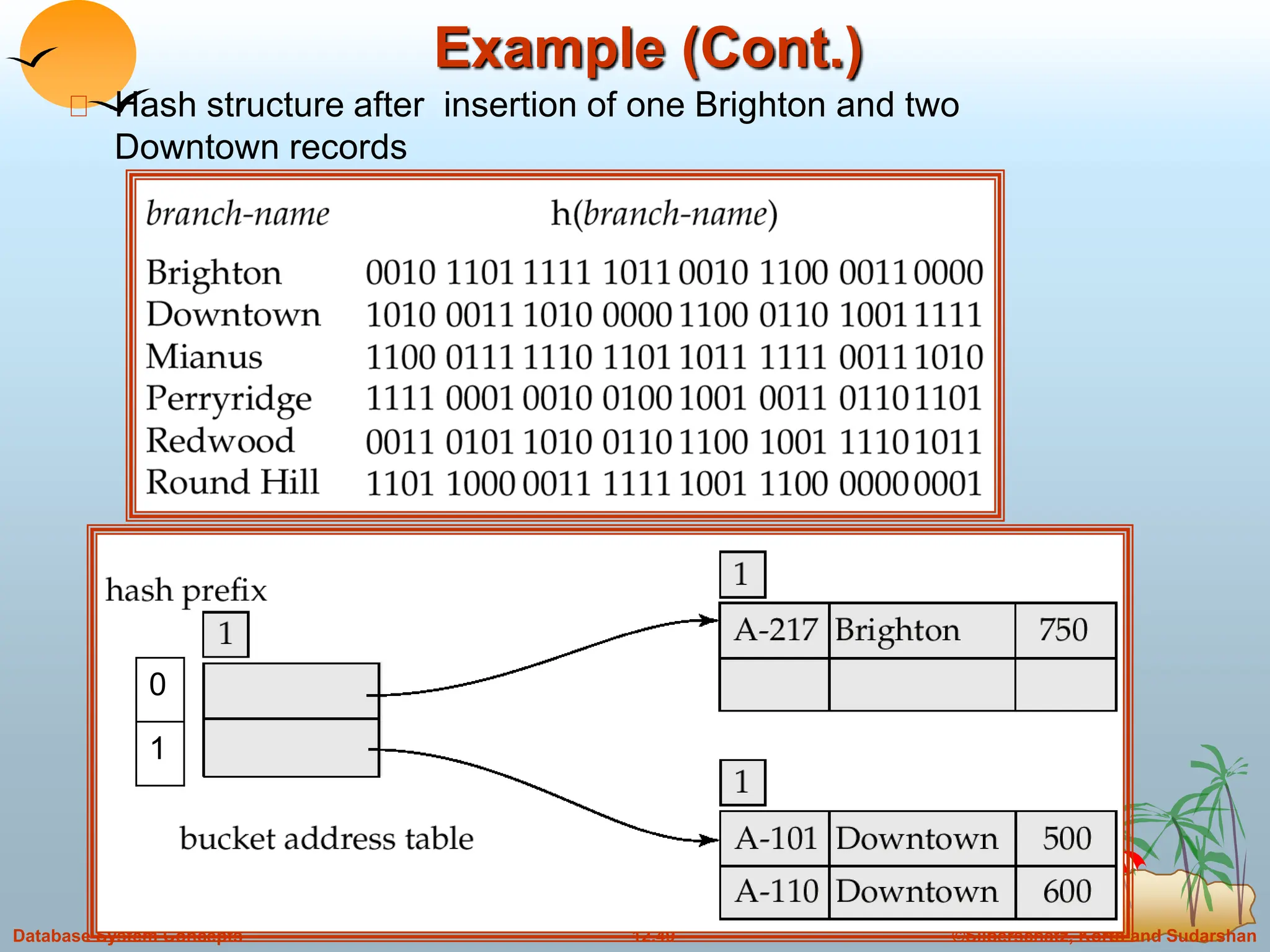
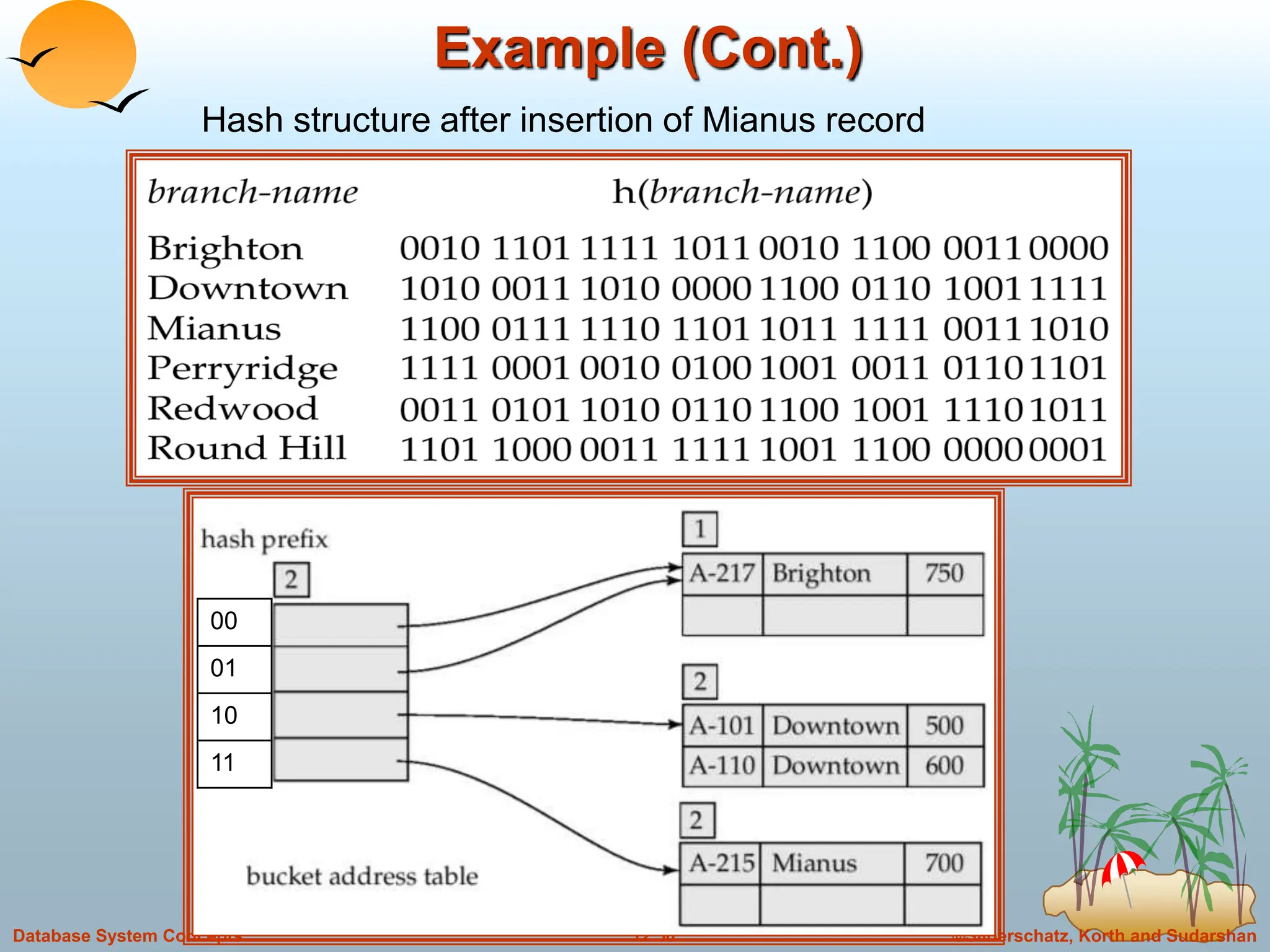
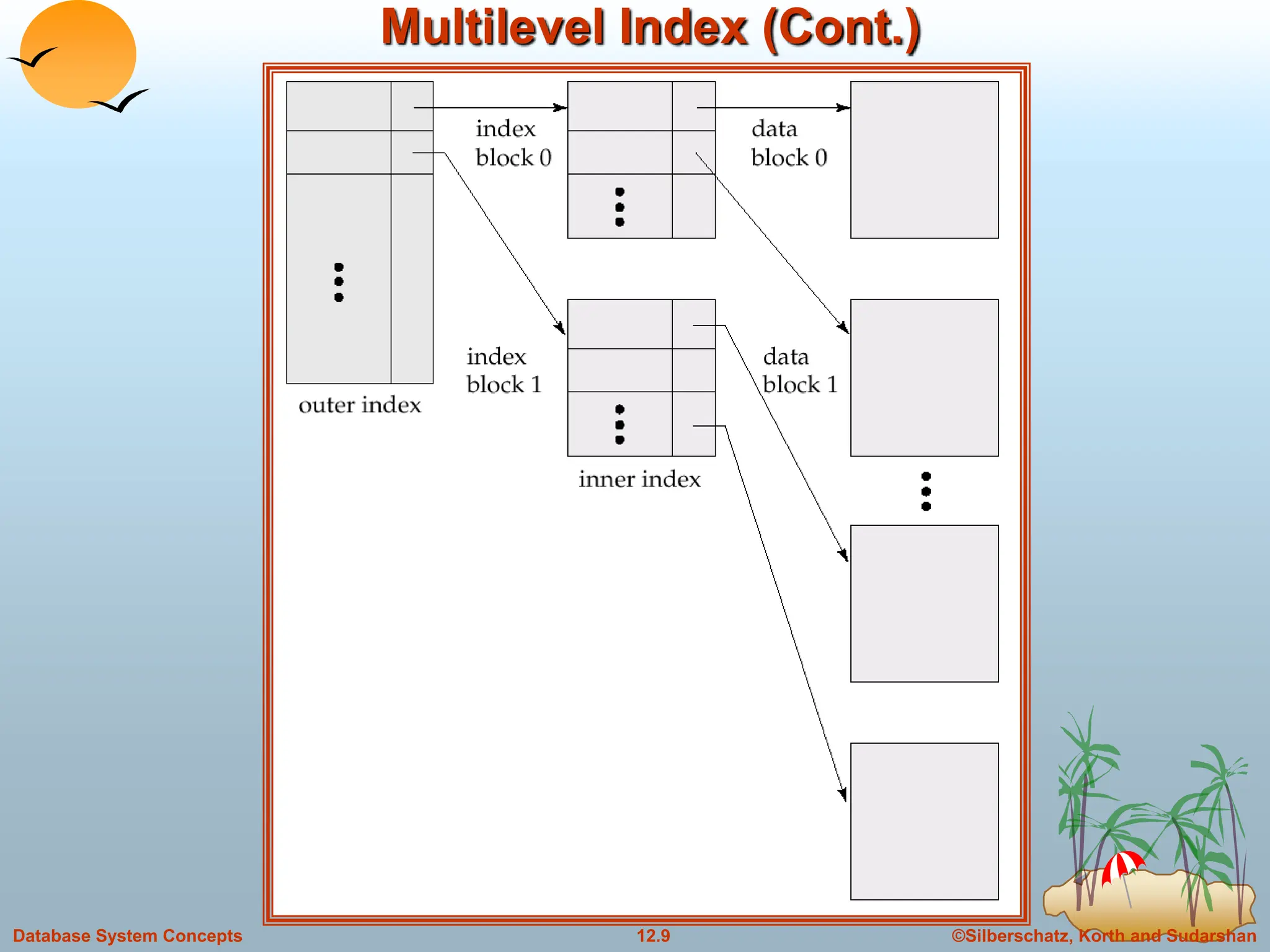
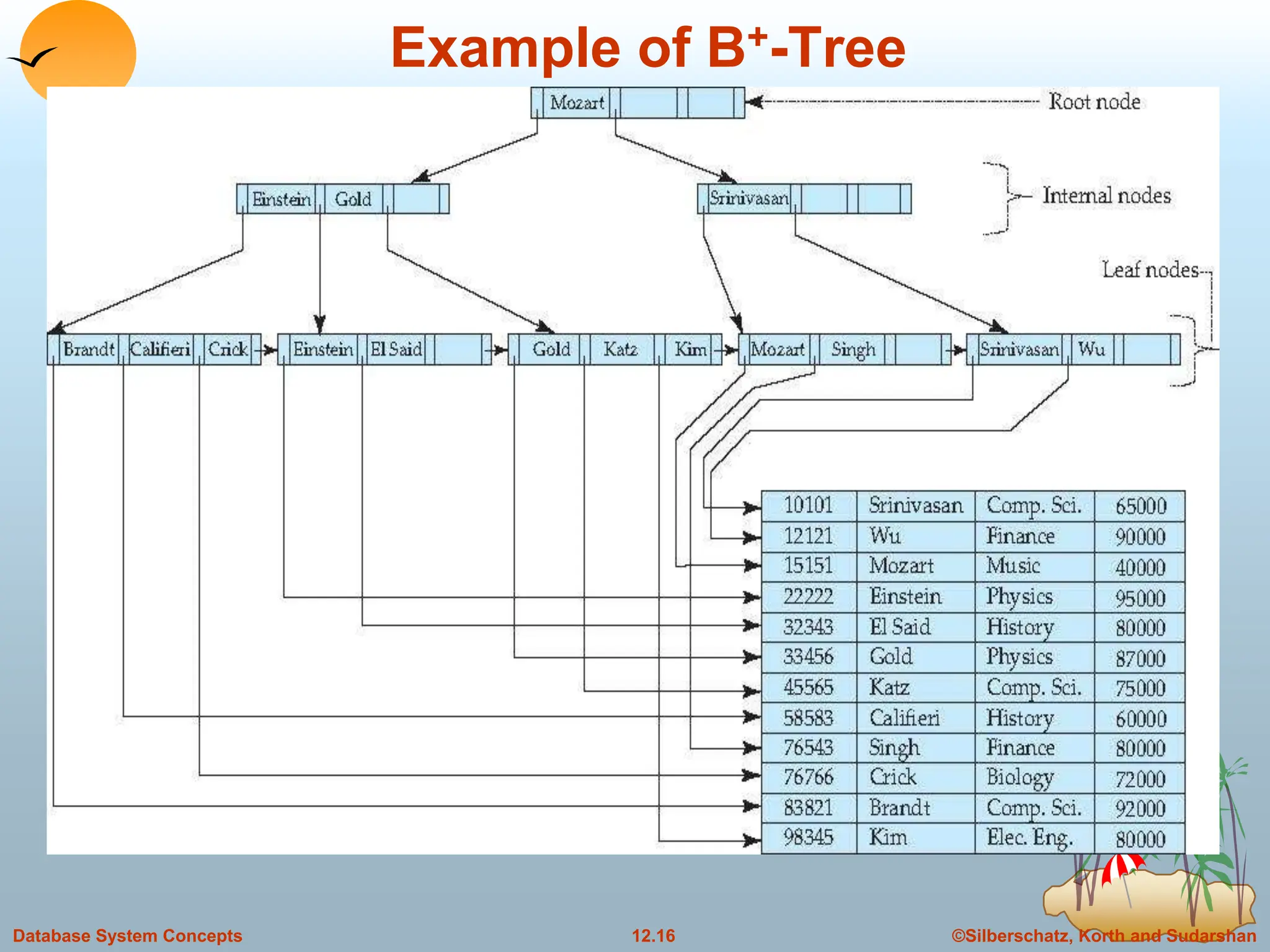
The document discusses indexing and hashing techniques for improving access speed to desired data in databases. It covers basic concepts of indexing like search keys and index files. The two main types of indices are ordered indices, where search keys are stored in sorted order, and hash indices, where keys are uniformly distributed across buckets using a hash function. The document then discusses different indexing structures like dense vs sparse files, multi-level indices, B+-tree indices, and static hashing. It also covers index update methods for insertion and deletion of records.















![©Silberschatz, Korth and Sudarshan
12.19
Database System Concepts
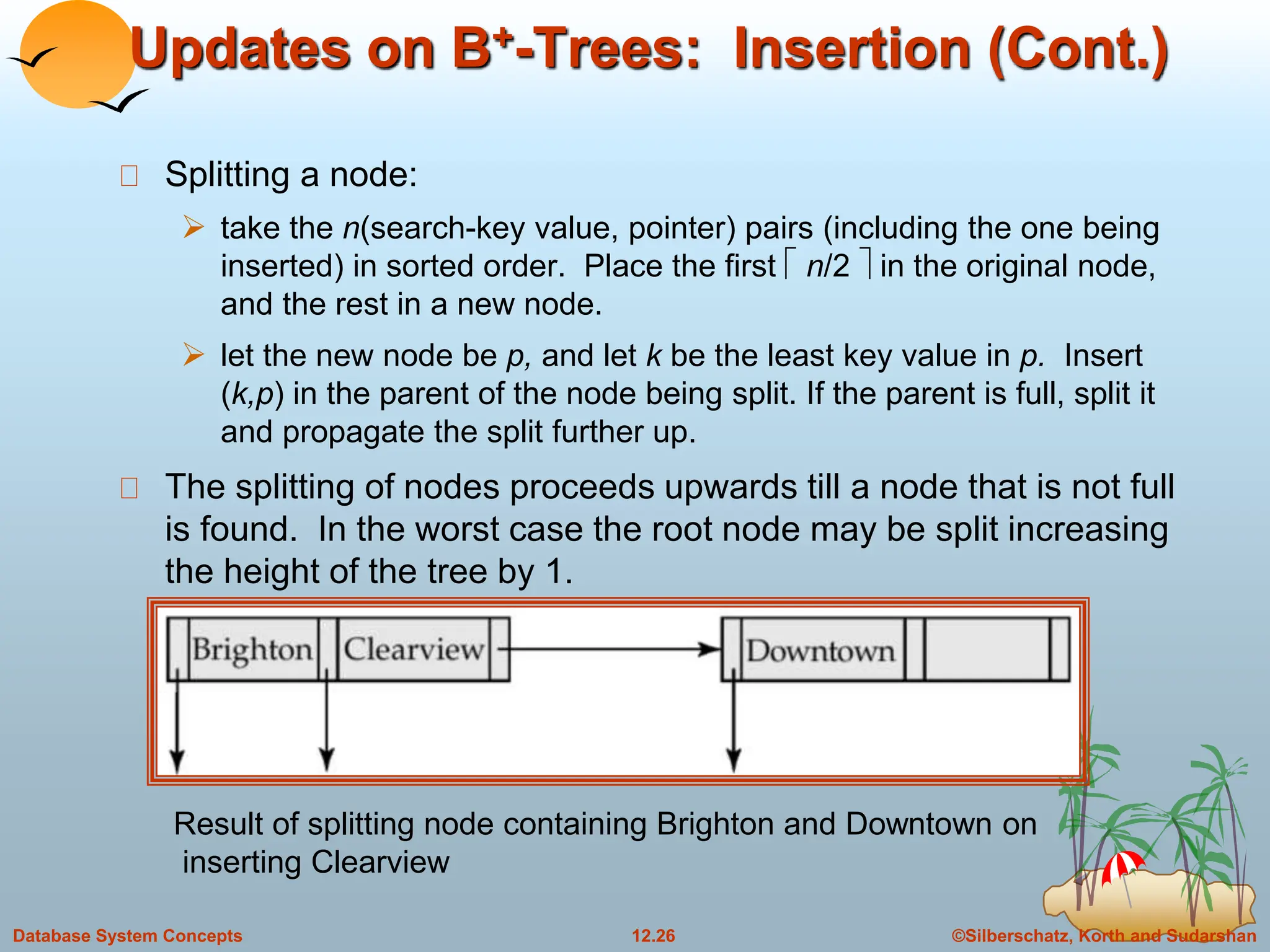
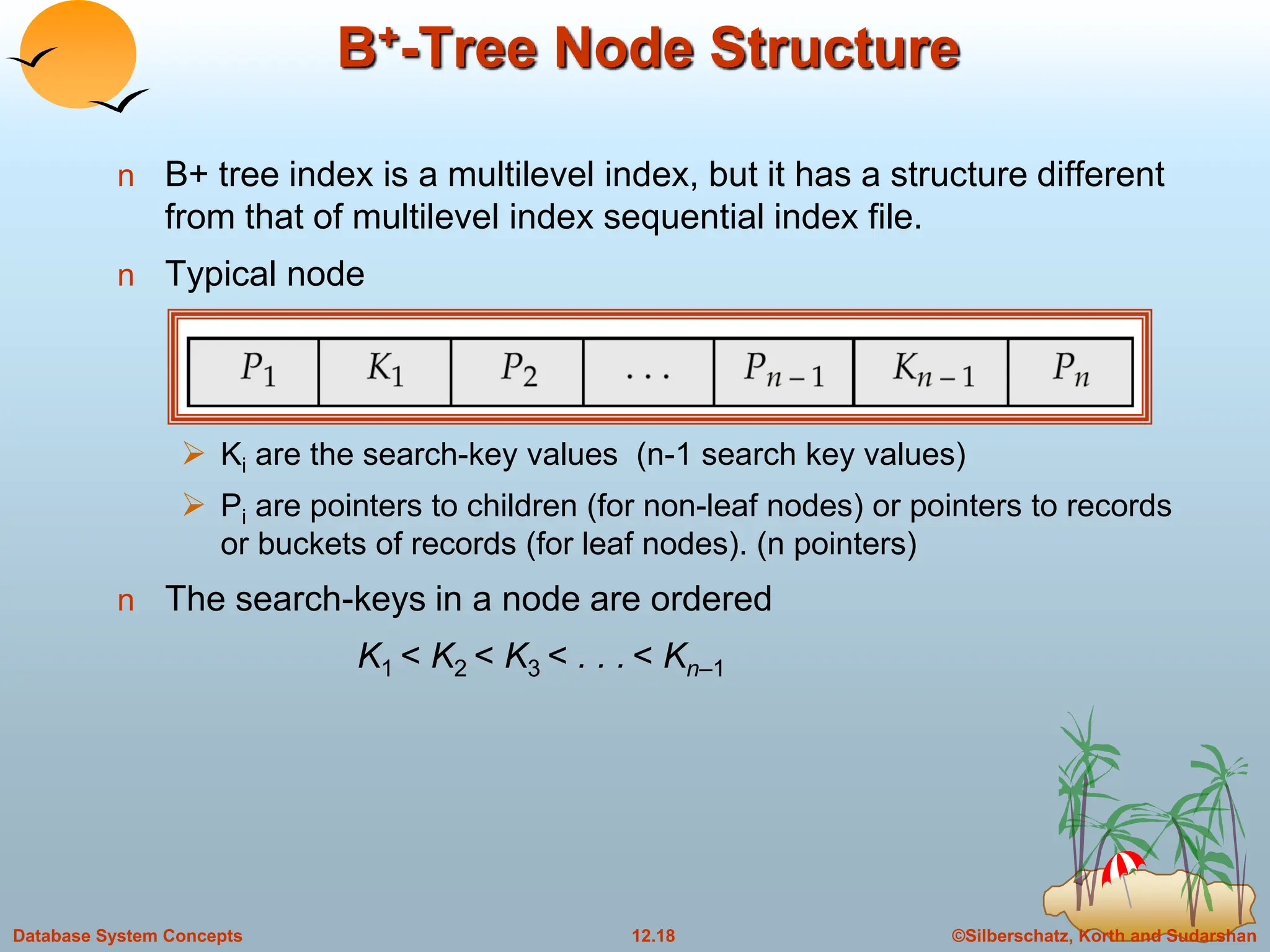
Leaf Nodes in B+-Trees
For i = 1, 2, . . ., n–1, pointer Pi either points to a file record with search-
key value Ki, or to a bucket of pointers to file records, each record
having search-key value Ki. Only need bucket structure if search-key
does not form a primary key.
Each leaf can hold up to n-1 values. Leaf can hold as few as [ (n-1)/2]
values. The ranges of values in each leaf do not overlap.
If Li, Lj are leaf nodes and i < j, Li’s search-key values are less than Lj’s
search-key values
Pn points to next leaf node in search-key order
Properties of a leaf node:](https://image.slidesharecdn.com/indexingandhashing-231029070843-5b37b27a/75/Indexing-and-Hashing-ppt-19-2048.jpg)


![©Silberschatz, Korth and Sudarshan
12.23
Database System Concepts
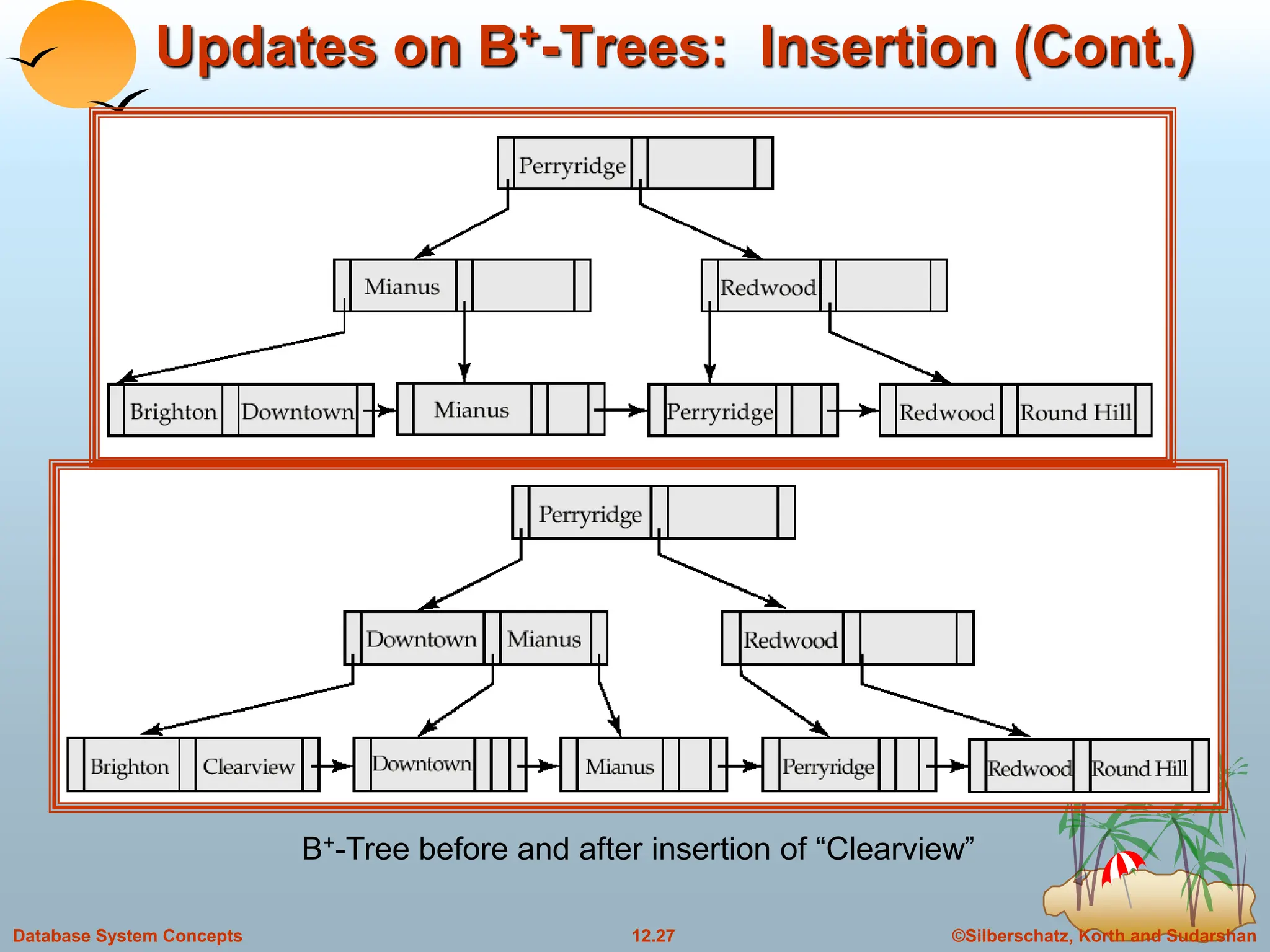
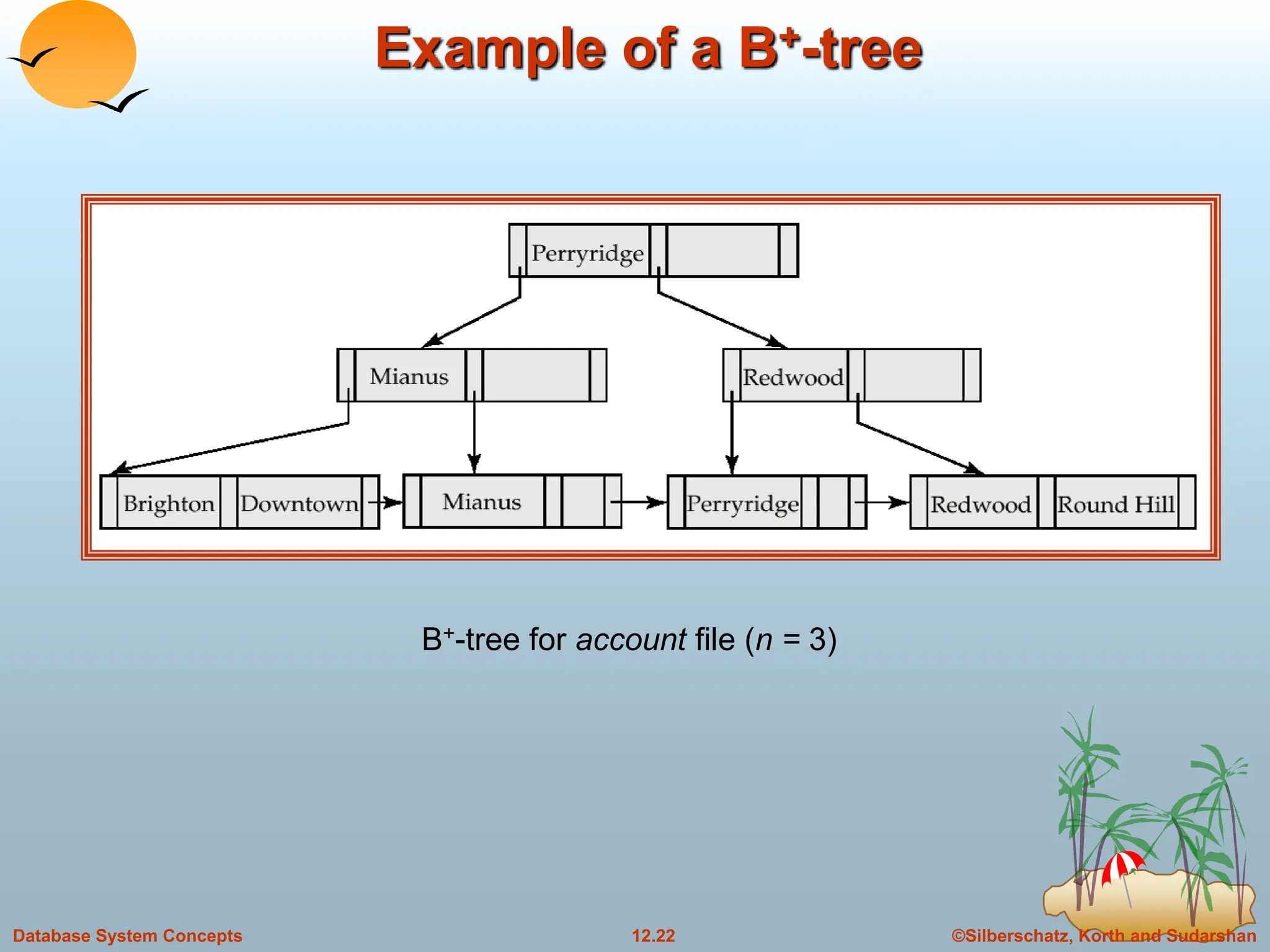
Example of B+-tree
Leaf nodes must have between 2 and 4 values
((n–1)/2 and n –1, with n = 5).
Non-leaf nodes other than root must have between 3
and 5 children ((n/2 and n with n =5).
Root must have at least 2 children fewer than [n/2]
pointers.
B+-tree for account file (n = 5)](https://image.slidesharecdn.com/indexingandhashing-231029070843-5b37b27a/75/Indexing-and-Hashing-ppt-23-2048.jpg)