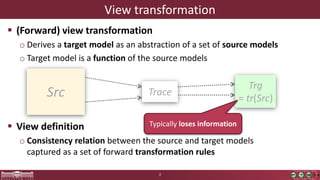
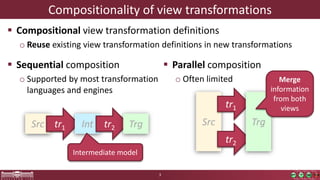
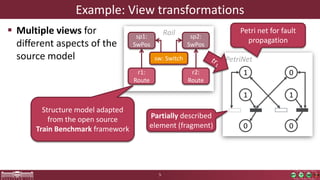
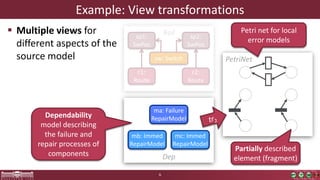
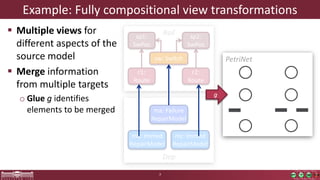
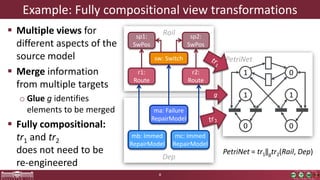
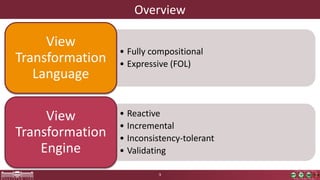
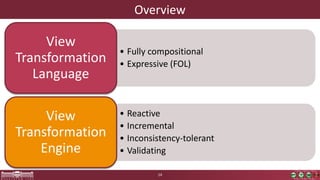
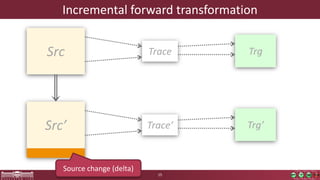
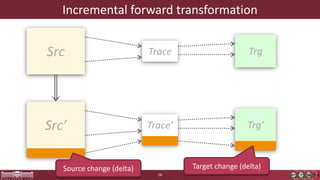
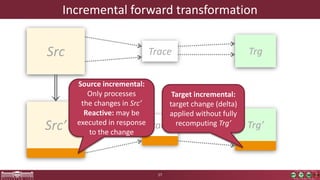
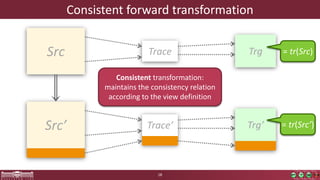
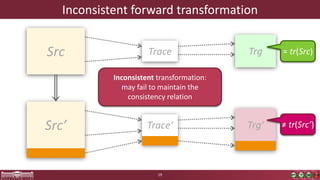
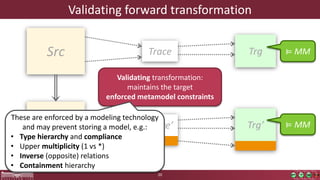
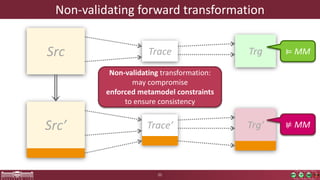
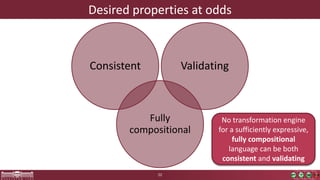
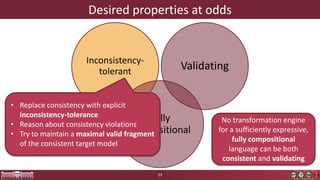
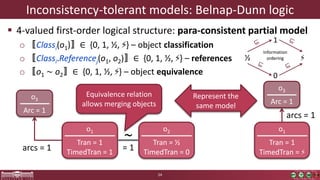
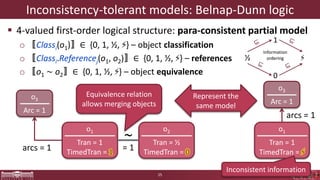
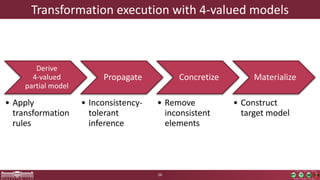
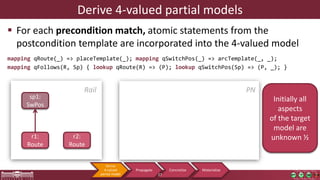
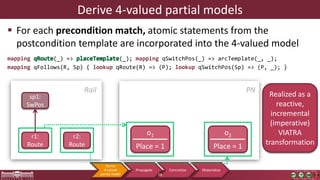
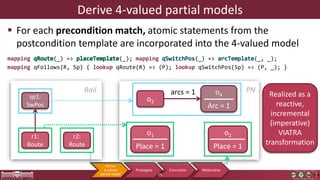
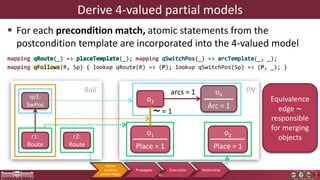
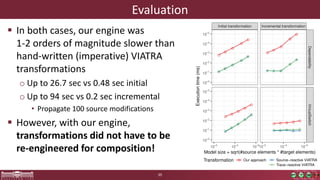
This document discusses incremental view model synchronization using partial models, focusing on compositional view transformations in the context of dependability evaluation for automotive systems. It elaborates on the challenges and techniques for deriving analysis models, including the use of a fully compositional view definition language and a validation engine. The evaluation indicates that the proposed engine, while slower than hand-written transformations, offers significant advantages in transformation composability without the need for re-engineering.

1. Budapest University of Technology and Economics
Department of Measurement and Information Systems
Budapest University of
Technology and Economics
Fault Tolerant Systems
Research Group
McGill University
Department of Mechanical
and Electrical Engineering
MTA-BME Cyber-Physical
Systems Research Group
Incremental View Model Synchronization
Using Partial Models
Kristóf Marussy, Oszkár Semeráth, Dániel Varró
1

2. View transformation
 (Forward) view transformation
o Derives a target model as an abstraction of a set of source models
o Target model is a function of the source models
 View definition
o Consistency relation between the source and target models
captured as a set of forward transformation rules
2
Src
Trg
= tr(Src)
Trace
Typically loses information

3. Compositionality of view transformations
 Compositional view transformation definitions
o Reuse existing view transformation definitions in new transformations
3
 Sequential composition
o Supported by most transformation
languages and engines
 Parallel composition
o Often limited
Src tr1 Int tr2 Trg Src
tr1
tr2
Trg
Merge
information
from both
views
Intermediate model

4. Compositionality of view transformations
 Compositional view transformation definitions
o Reuse existing view transformation definitions in new transformations
4
 Sequential composition
o Supported by most transformation
languages and engines
 Parallel composition
o Often limited
Src tr1 Int tr2 Trg Src
tr1
tr2
Trg
Merge
information
from both
views
Intermediate model
Motivation: Deriving stochastic Petri net analysis models for
dependability evaluation of critical embedded automotive systems
in an industrial collaboration:
• What is the mean-time-to-first-failure in the system?
• What is the probability of the different hazards?
• Which architecture candidate is the most reliable?
Transformations for different aspects of the system were created
individually, and composed in parallel to derive
the complete analysis model.

5. Example: View transformations
 Multiple views for
different aspects of the
source model
5
sp1:
SwPos
sp2:
SwPos
r1:
Route
r2:
Route
sw: Switch
1
1
0
0
1
0
Rail
PetriNet
Partially described
element (fragment)
Petri net for fault
propagation
Structure model adapted
from the open source
Train Benchmark framework

6. Example: View transformations
sp1:
SwPos
sp2:
SwPos
r1:
Route
r2:
Route
sw: Switch
Rail
6
ma: Failure
RepairModel
mb: Immed
RepairModel
mc: Immed
RepairModel
Dep
PetriNet
Partially described
element (fragment)
Petri net for local
error models
Dependability
model describing
the failure and
repair processes of
components
 Multiple views for
different aspects of the
source model

7. Example: Fully compositional view transformations
7
sp1:
SwPos
sp2:
SwPos
r1:
Route
r2:
Route
sw: Switch
ma: Failure
RepairModel
Rail
mb: Immed
RepairModel
mc: Immed
RepairModel
Dep
PetriNet
g
 Multiple views for
different aspects of the
source model
 Merge information
from multiple targets
o Glue g identifies
elements to be merged

8. Example: Fully compositional view transformations
 Multiple views for
different aspects of the
source model
 Merge information
from multiple targets
o Glue g identifies
elements to be merged
 Fully compositional:
tr1 and tr2
does not need to be
re-engineered
8
sp1:
SwPos
sp2:
SwPos
r1:
Route
r2:
Route
sw: Switch
ma: Failure
RepairModel
1
1
0
0
1
0
Rail
mb: Immed
RepairModel
mc: Immed
RepairModel
Dep
PetriNet
g
PetriNet = tr1‖gtr2(Rail, Dep)

9. Overview
• Fully compositional
• Expressive (FOL)
View
Transformation
Language
• Reactive
• Incremental
• Inconsistency-tolerant
• Validating
View
Transformation
Engine
9

10. A fully compositional view definition language
 Explicitly reuses the VIATRA Query language
o precondition patterns
o postcondition templates
 Templates: conjunction of atomic statements
mapping qRoute(_) => placeTemplate(_);
mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) {
lookup qRoute(R) => (P);
lookup qSwitchPos(Sp) => (P, _); }
10

11. A fully compositional view definition language
 Explicitly reuses the VIATRA Query language
o precondition patterns
o postcondition templates
 Templates: conjunction of atomic statements
mapping qRoute(_) => placeTemplate(_);
mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) {
lookup qRoute(R) => (P);
lookup qSwitchPos(Sp) => (P, _); }
11
Precondition pattern
pattern qRoute(R) {
Route(R);
}
Postcondition template
pattern placeTemplate(P) {
Place(P);
}

12. A fully compositional view definition language
 Explicitly reuses the VIATRA Query language
o precondition patterns
o postcondition templates
 Templates: conjunction of atomic statements
mapping qRoute(_) => placeTemplate(_);
mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) {
lookup qRoute(R) => (P);
lookup qSwitchPos(Sp) => (P, _); }
12
Precondition pattern
pattern qSwitchPos(Sp) {
SwPos(R);
}
Postcondition template
pattern arcTemplate(P, A) {
Arc(A);
Place.arcs(P, A);
}

13. A fully compositional view definition language
 Explicitly reuses the VIATRA Query language
o precondition patterns
o postcondition templates
 Templates: conjunction of atomic statements
mapping qRoute(_) => placeTemplate(_);
mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) {
lookup qRoute(R) => (P);
lookup qSwitchPos(Sp) => (P, _); }
13
Glue precondition pattern
pattern qFollows(R, Sp) {
Route.follows(R, Sp);
} Merging by Prolog-style
variable unification
Trace lookup

14. Overview
• Fully compositional
• Expressive (FOL)
View
Transformation
Language
• Reactive
• Incremental
• Inconsistency-tolerant
• Validating
View
Transformation
Engine
14

15. Incremental forward transformation
15
Src TrgTrace
Src’ Trg’Trace’
Source change (delta)

16. Incremental forward transformation
16
Src TrgTrace
Src’ Trg’Trace’
Source change (delta) Target change (delta)

17. Incremental forward transformation
17
Src TrgTrace
Src’ Trg’Trace’
Source incremental:
Only processes
the changes in Src’
Reactive: may be
executed in response
to the change
Target incremental:
target change (delta)
applied without fully
recomputing Trg’

18. Consistent forward transformation
18
Src TrgTrace
Src’ Trg’Trace’
Consistent transformation:
maintains the consistency relation
according to the view definition
= tr(Src)
= tr(Src’)

19. Inconsistent forward transformation
19
Src TrgTrace
Src’ Trg’Trace’
Inconsistent transformation:
may fail to maintain the
consistency relation
= tr(Src)
≠ tr(Src’)

20. Validating forward transformation
20
Src TrgTrace
Src’ Trg’Trace’
Validating transformation:
maintains the target
enforced metamodel constraints
⊨ MM
⊨ MM
These are enforced by a modeling technology
and may prevent storing a model, e.g.:
• Type hierarchy and compliance
• Upper multiplicity (1 vs *)
• Inverse (opposite) relations
• Containment hierarchy

21. Non-validating forward transformation
21
Src TrgTrace
Src’ Trg’Trace’
Non-validating transformation:
may compromise
enforced metamodel constraints
to ensure consistency
⊨ MM
⊭ MM

22. Desired properties at odds
22
Consistent
Fully
compositional
Validating
No transformation engine
for a sufficiently expressive,
fully compositional
language can be both
consistent and validating

23. Desired properties at odds
23
Inconsistency-
tolerant
Fully
compositional
Validating
No transformation engine
for a sufficiently expressive,
fully compositional
language can be both
consistent and validating
• Replace consistency with explicit
inconsistency-tolerance
• Reason about consistency violations
• Try to maintain a maximal valid fragment
of the consistent target model

24. Inconsistency-tolerant models: Belnap-Dunn logic
 4-valued first-order logical structure: para-consistent partial model
o 〚Classi(o1)〛∈ {0, 1, ½, ⚡} – object classification
o 〚Classi.Referencej(o1, o2)〛∈ {0, 1, ½, ⚡} – references
o 〚o1 ∼ o2〛∈ {0, 1, ½, ⚡} – object equivalence
24
o1
Tran = 1
TimedTran = 1
o2
Tran = ½
TimedTran = 0
∼
= 1
o3
Arc = 1
arcs = 1
Equivalence relation
allows merging objects
o1
Tran = 1
TimedTran = ⚡
o3
Arc = 1
Represent the
same model
arcs = 1

25. Inconsistency-tolerant models: Belnap-Dunn logic
 4-valued first-order logical structure: para-consistent partial model
o 〚Classi(o1)〛∈ {0, 1, ½, ⚡} – object classification
o 〚Classi.Referencej(o1, o2)〛∈ {0, 1, ½, ⚡} – references
o 〚o1 ∼ o2〛∈ {0, 1, ½, ⚡} – object equivalence
25
o1
Tran = 1
TimedTran = 1
o2
Tran = ½
TimedTran = 0
∼
= 1
o3
Arc = 1
arcs = 1
Equivalence relation
allows merging objects
Represent the
same model
o1
Tran = 1
TimedTran = ⚡
o3
Arc = 1
Inconsistent information
arcs = 1

26. Transformation execution with 4-valued models
Derive
4-valued
partial model
• Apply
transformation
rules
Propagate
• Inconsistency-
tolerant
inference
Concretize
• Remove
inconsistent
elements
Materialize
• Construct
target model
26

27. Derive 4-valued partial models
 For each precondition match, atomic statements from the
postcondition template are incorporated into the 4-valued model
mapping qRoute(_) => placeTemplate(_); mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) { lookup qRoute(R) => (P); lookup qSwitchPos(Sp) => (P, _); }
sp1:
SwPos
r1:
Route
r2:
Route
Rail PN
Initially all
aspects
of the target
model are
unknown ½
Derive
4-valued
partial model
Propagate Concretize Materialize
27

28. Derive 4-valued partial models
 For each precondition match, atomic statements from the
postcondition template are incorporated into the 4-valued model
mapping qRoute(_) => placeTemplate(_); mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) { lookup qRoute(R) => (P); lookup qSwitchPos(Sp) => (P, _); }
sp1:
SwPos
r1:
Route
r2:
Route
Rail
o1
Place = 1
o2
Place = 1
PN
Realized as a
reactive,
incremental
(imperative)
VIATRA
transformation
Derive
4-valued
partial model
Propagate Concretize Materialize
28

29. Derive 4-valued partial models
 For each precondition match, atomic statements from the
postcondition template are incorporated into the 4-valued model
mapping qRoute(_) => placeTemplate(_); mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) { lookup qRoute(R) => (P); lookup qSwitchPos(Sp) => (P, _); }
sp1:
SwPos
r1:
Route
r2:
Route
Rail o4
Arc = 1
o1
Place = 1
o2
Place = 1
o3
arcs = 1 PN
Realized as a
reactive,
incremental
(imperative)
VIATRA
transformation
Derive
4-valued
partial model
Propagate Concretize Materialize
29

30. Derive 4-valued partial models
 For each precondition match, atomic statements from the
postcondition template are incorporated into the 4-valued model
mapping qRoute(_) => placeTemplate(_); mapping qSwitchPos(_) => arcTemplate(_, _);
mapping qFollows(R, Sp) { lookup qRoute(R) => (P); lookup qSwitchPos(Sp) => (P, _); }
sp1:
SwPos
r1:
Route
r2:
Route
Rail o4
Arc = 1
o1
Place = 1
o2
Place = 1
o3
arcs = 1
∼ = 1
PN
Equivalence
edge ∼
responsible
for merging
objects
Derive
4-valued
partial model
Propagate Concretize Materialize
30

31. Propagation and concretization
 We turned enforced metamodel constraints into
propagation (inference) rules applied to the 4-valued model
o E.g.,
1⊑ 𝐶𝑙𝑎𝑠𝑠1 𝑜 , 𝐶𝑙𝑎𝑠𝑠1 𝑖𝑠 𝑎 𝑠𝑢𝑏𝑐𝑙𝑎𝑠𝑠 𝑜𝑓 𝐶𝑙𝑎𝑠𝑠2
1⊑ 𝐶𝑙𝑎𝑠𝑠2(𝑜)
o Unsatisfied constraints are discovered as ⚡ inconsistencies
Derive
4-valued
partial model
Propagate Concretize Materialize
31

32. Propagation and concretization
 We turned enforced metamodel constraints into
propagation (inference) rules applied to the 4-valued model
o E.g.,
1⊑ 𝐶𝑙𝑎𝑠𝑠1 𝑜 , 𝐶𝑙𝑎𝑠𝑠1 𝑖𝑠 𝑎 𝑠𝑢𝑏𝑐𝑙𝑎𝑠𝑠 𝑜𝑓 𝐶𝑙𝑎𝑠𝑠2
1⊑ 𝐶𝑙𝑎𝑠𝑠2(𝑜)
o Unsatisfied constraints are discovered as ⚡ inconsistencies
 Concretize the 4-valued partial model to {0, 1} truth values only
o Monotonicity of enforced metamodel constraints
 constraints can be satisfied by omitting inconsistent objects
o No extraneous output: Set all unknown ½ values to 0
o No invalid output: Remove all inconsistent ⚡ elements
Derive
4-valued
partial model
Propagate Concretize Materialize
32

33. Incremental materialization
 Materialization constructs a regular instance model according to the
concretized partial model
o The output model contains all information from the consistent target model,
except the elements that would violate enforced metamodel constraints
 Propagation, concretization and materialization steps are
implemented as incremental, reactive VIATRA transformations
o Together with the 4-valued model construction steps,
end-to-end traceability and reactive execution is provided
Derive
4-valued
partial model
Propagate Concretize Materialize
33

34. Evaluation
 Compared transformation execution in two case studies
o Dependability model
• “Compiler” behavior, target model 3x larger than source
• Up to 25K source, 72K target objects
o Filtering and aggregation
• “Abstraction” behavior, source 500x larger than target model
• Up to 425K source, 9K target objects
 Baseline: two styles of hand-written (imperative)
VIATRA transformation
34

35. Evaluation
 In both cases, our engine was
1-2 orders of magnitude slower than
hand-written (imperative) VIATRA
transformations
o Up to 26.7 sec vs 0.48 sec initial
o Up to 94 sec vs 0.2 sec incremental
• Propagate 100 source modifications
 However, with our engine,
transformations did not have to be
re-engineered for composition!
35

36. Summary
36
https://github.com/FTSRG/viewmodel