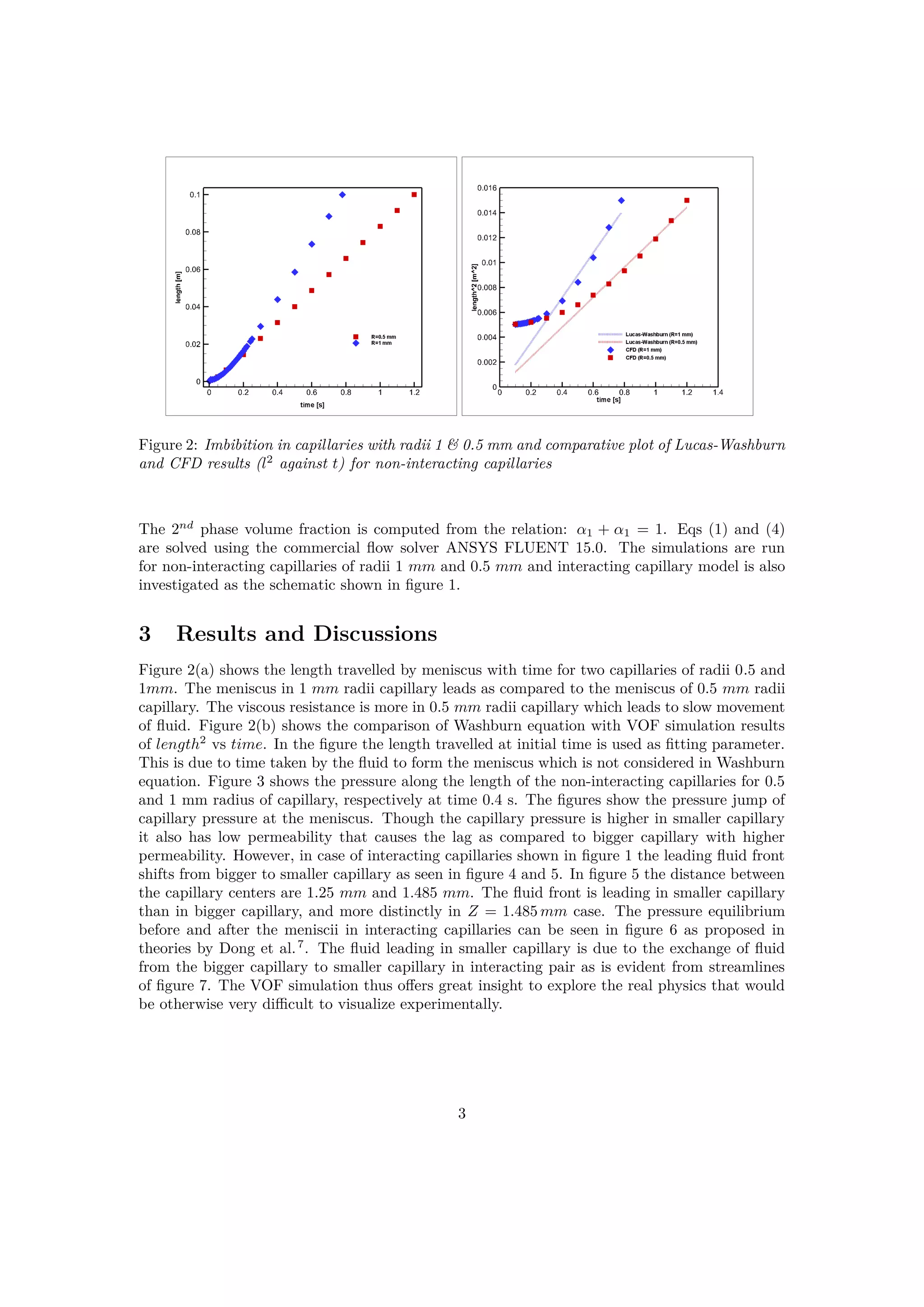
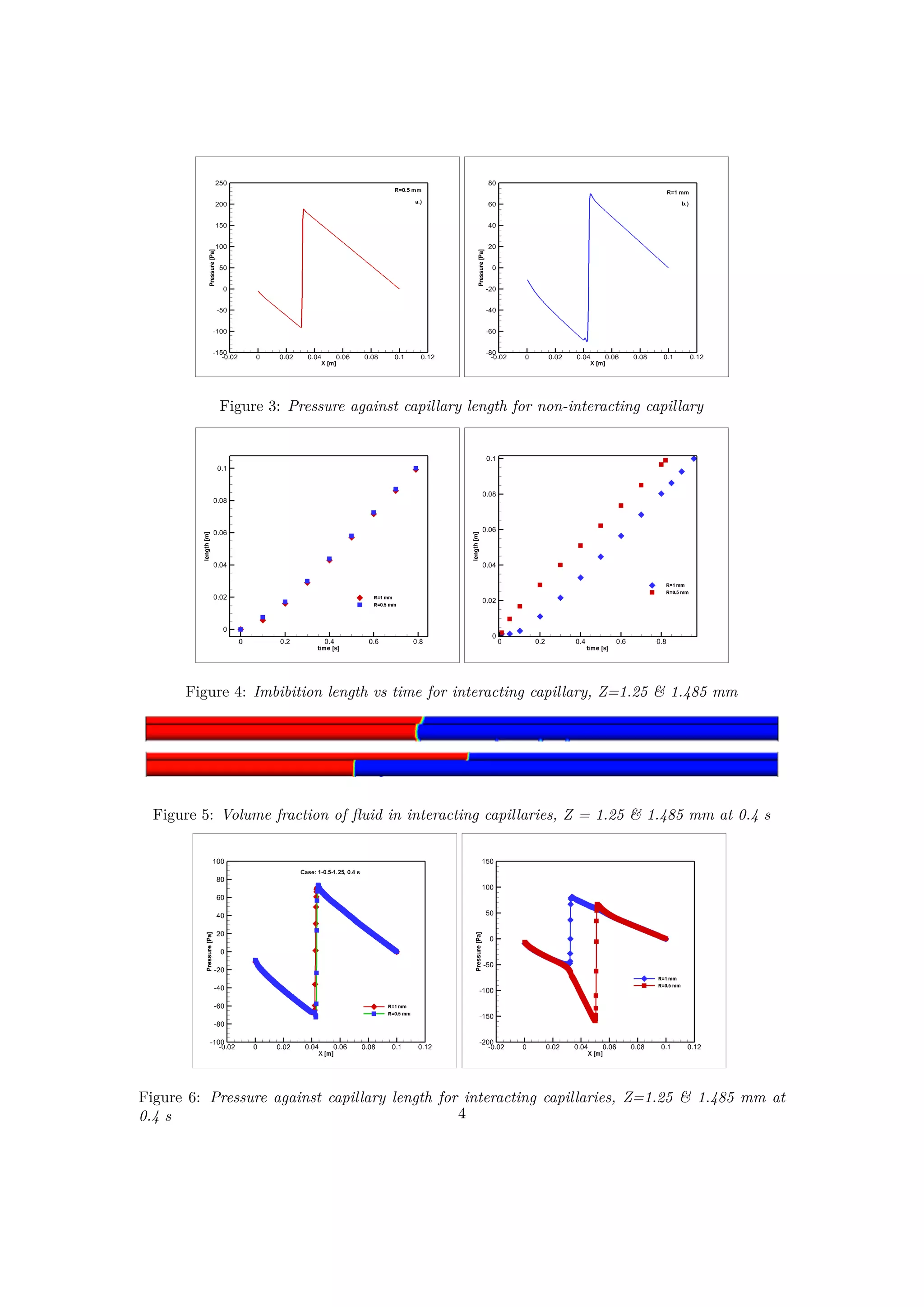
This study investigates spontaneous imbibition dynamics in both non-interacting and interacting capillaries using a volume of fluid model. It reveals that while traditional models like the Washburn equation fail to explain early-time meniscus formation in non-interacting capillaries, the behavior of interacting capillaries is heavily influenced by connectivity, allowing them to behave like a single capillary when more connected. The findings enhance the understanding of fluid flow in fractured reservoirs, providing valuable insights into capillary action in porous media.

1. A-2315
Imbibition dynamics in interacting capillaries
G. Visavale, S. Ashraf and J. Phirani∗
Department of Chemical Engineering, Indian Institute of Technology Delhi, Hauz Khas,
New Delhi 110016, India.
visavaleganesh@gmail.com
Abstract
Spontaneous imbibition has long been known to have significant role in recovering oil
from low permeability fractured reservoirs. Though the fundamental theory of capillarity is
known for about a century by the works of Hagen Poiseuille and then by Lucas and Washburn
they do not entirely describe the phenomena. The capillary action at early times i.e. in
the inertial regime and the dynamics for interacting capillaries remain unexplained. In the
present work, we report the numerical investigations using volume of fluid (VOF) model for
the spontaneous imbibition in non-interacting and interacting capillaries. Capillaries with
radii 0.5 and 1 mm, length 100 mm were selected for studying the effect of non-interacting
and interacting nature on the imbibition dynamics. The two interacting capillary cases were
with centre to centre distance of 1.25 and 1.485 mm. The interacting capillary model shows
that if connectivity is more capillaries will behave as single capillary, but if connectivity is
less meniscus leads in smaller radii capillary. The study will help us in understanding the
physics of flow in fractured reservoirs.
1 Introduction
In spontaneous imbibition the wetting fluid (generally water) is sucked in pores due to capillary
forces. The fundamental knowledge of the flow due to capillary forces is known for past century.
The theoretical foundations were laid by Hagen Poiseuille for flow in pipes using which Lucas
and Washburn1
found the meniscus position variation with time due to capillary forces. For
capillaries of uniform cross-section the rate of imbibition obeys the law stated by Lucas-Washburn
as: l2
= Dt, where l represents the imbibed distance through which the fluid has moved in
time t and D is the coefficient that depends on the characteristics of the capillary and the
fluids. However these classical equations do not entirely describe the capillary invasion at the
inertial regime at very short times, in non-uniform geometries and for interacting nature of
capillaries i.e connected capillaries that are present in porous media. Pores found in reservoir
have random geometrical orientations, are interacting in nature and the imbibition of the fluid
into these random microchannels cannot be described analytically. A reservoir made of for
example sandstones, limestones, etc. consists of an interconnected, three dimensional (3-D)
network of pores or capillaries. As a result, these interconnected capillaries with the fluids
present in adjacent capillaries interact with each other. Dong et al.2
(2005); Dong3
(2006); Ruth
and Bartley4
(2011); have developed 1-D models to simulate immiscible displacement in porous
∗corresponding author: jphirani@chemical.iitd.ac.in
1

2. Figure 1: Schematic of interacting and non-interacting capillaries, Z is the centre to centre
distance between capillaries of radii 1 and 0.5 mm
media. However their work also do not consider the entry effects (inertial regime) and the degree
of connectivity between the interacting capillaries.
In the present work, we report the numerical investigations of the spontaneous imbibition
in non-interacting and interacting capillaries and investigate the effect of degree of connectivity
on the imbibition pattern. These results will help us in understanding the physics of flow in
fractured reservoirs.
2 Computational model
In this study, the volume of fluid (VOF) method (Hirt and Nichols5
, 1981) was used to simulate
the spontaneous imbibition of a wetting fluid of µ = 0.001 kg/ms, ρ=998 kg/m3
, in a capillary
filled with a non-wetting fluid of identical viscosity. The interfacial tension between the fluids
is considered to be 0.072N/m. The fluid phases are considered incompressible and the flow
is assumed to be Newtonian and laminar. In VOF method, the phases are identified by their
volume fraction (αi, i = 1, 2) in a computational cell6
. When αi = 1; the cell is filled with 1st
phase and when αi = 0 cell is filled with the 2nd
phase and if 0 < αi < 1; the cell contains the
interface between the 1st
and 2nd
phases. A single set of Navier-Stokes equation is solved for the
incompressible Newtonian flow:
∂
∂t
(ρv) + · (ρvv) = −δp + [µ( v + ( v)T
)] + ρg + F (1)
where F is the surface tension force per unit volume. When a computational cell is not entirely
occupied by one phase, mixture properties described as:
ρ = α1ρ1 + (1 − α1)ρ2 (2)
µ = α1µ1 + (1 − α1)µ2 (3)
For the qth
phase, advection equation is written as:
∂
∂t
(α1ρ1) + · (α1ρ1v1) = 0 (4)
2

3. Figure 2: Imbibition in capillaries with radii 1 & 0.5 mm and comparative plot of Lucas-Washburn
and CFD results (l2
against t) for non-interacting capillaries
The 2nd
phase volume fraction is computed from the relation: α1 + α1 = 1. Eqs (1) and (4)
are solved using the commercial flow solver ANSYS FLUENT 15.0. The simulations are run
for non-interacting capillaries of radii 1 mm and 0.5 mm and interacting capillary model is also
investigated as the schematic shown in figure 1.
3 Results and Discussions
Figure 2(a) shows the length travelled by meniscus with time for two capillaries of radii 0.5 and
1mm. The meniscus in 1 mm radii capillary leads as compared to the meniscus of 0.5 mm radii
capillary. The viscous resistance is more in 0.5 mm radii capillary which leads to slow movement
of fluid. Figure 2(b) shows the comparison of Washburn equation with VOF simulation results
of length2
vs time. In the figure the length travelled at initial time is used as fitting parameter.
This is due to time taken by the fluid to form the meniscus which is not considered in Washburn
equation. Figure 3 shows the pressure along the length of the non-interacting capillaries for 0.5
and 1 mm radius of capillary, respectively at time 0.4 s. The figures show the pressure jump of
capillary pressure at the meniscus. Though the capillary pressure is higher in smaller capillary
it also has low permeability that causes the lag as compared to bigger capillary with higher
permeability. However, in case of interacting capillaries shown in figure 1 the leading fluid front
shifts from bigger to smaller capillary as seen in figure 4 and 5. In figure 5 the distance between
the capillary centers are 1.25 mm and 1.485 mm. The fluid front is leading in smaller capillary
than in bigger capillary, and more distinctly in Z = 1.485 mm case. The pressure equilibrium
before and after the meniscii in interacting capillaries can be seen in figure 6 as proposed in
theories by Dong et al.7
. The fluid leading in smaller capillary is due to the exchange of fluid
from the bigger capillary to smaller capillary in interacting pair as is evident from streamlines
of figure 7. The VOF simulation thus offers great insight to explore the real physics that would
be otherwise very difficult to visualize experimentally.
3

4. Figure 3: Pressure against capillary length for non-interacting capillary
Figure 4: Imbibition length vs time for interacting capillary, Z=1.25 & 1.485 mm
Figure 5: Volume fraction of fluid in interacting capillaries, Z = 1.25 & 1.485 mm at 0.4 s
Figure 6: Pressure against capillary length for interacting capillaries, Z=1.25 & 1.485 mm at
0.4 s 4

5. Figure 7: Streamlines near meniscii region showing transfer of fluid from R=1 mm to R=0.5
mm for cases Z=1.25 and 1.485 mm
4 Conclusions
We successfully investigate the spontaneous imbibition in non-interacting and interacting cap-
illaries with fluids of equal viscosities. In non-interacting capillaries the VOF simulation shows
that Washburn equation is not able to capture the meniscus formation phenomena at early
times. The interacting capillary model shows that if connectivity is more capillaries will behave
as single capillary, but if connectivity is less meniscus leads in smaller radii capillary. VOF
provides insights in analysis of spontaneous imbibition in capillaries enabling good visualization
and tracking of interface (meniscii) between the two fluids.
References
1. Edward W. Washburn. The dynamics of capillary flow. Phys. Rev., Mar 1921.
2. Mingzhe Dong, Francis AL Dullien, Liming Dai, and Daiming Li. Immiscible displacement
in the interacting capillary bundle model part i. development of interacting capillary bundle
model. Transport in Porous media, 59(1):1–18, 2005.
3. Mingzhe Dong, Francis AL Dullien, Liming Dai, and Daiming Li. Immiscible displacement
in the interacting capillary bundle model part ii. applications of model and comparison of
interacting and non-interacting capillary bundle models. Transport in Porous media, 63(2):
289–304, 2006.
4. Douglas Ruth and Jonathan Bartley. Capillary tube models with interaction between the
tubes [a note on “immiscible displacement in the interacting capillary bundle model part i.
development of interacting capillary bundle model”, by dong, m., dullien, fal, dai, l. and li,
d., 2005, transport porous media]. Transport in porous media, 86(2):479–482, 2011.
5. Cyril W Hirt and Billy D Nichols. Volume of fluid (vof) method for the dynamics of free
boundaries. Journal of computational physics, 39(1):201–225, 1981.
6. Ansys Fluent Ansys. 14.0 theory guide. ANSYS Inc, 2011.
7. Mingzhe Dong, Jun Zhou, et al. Characterization of waterflood saturation profile histories by
the ‘complete’capillary number. Transport in porous media, 31(2):213–237, 1998.
5