Embed presentation
Downloaded 56 times

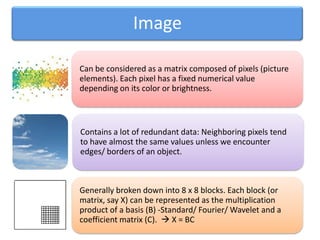

![B = [ b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 ] where b0, b1,.., b7 are 8 x 1 linearly independent vectors.](https://image.slidesharecdn.com/imagecompression-110518050905-phpapp01/85/Image-compression-4-320.jpg)
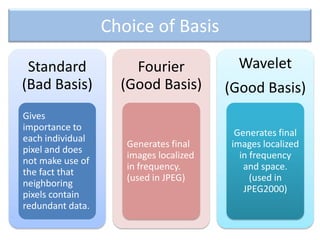

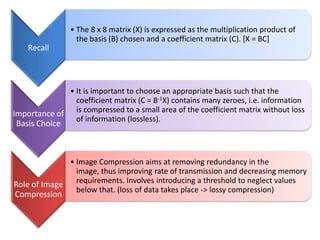


A basis is a set of linearly independent vectors that can be linearly combined to represent any vector in a given vector space, such as the 8x8 matrix representing an image. A good basis for image compression has more low-frequency vectors that imply less variation in pixel values across the image, and fewer high-frequency vectors that imply more variation. There are several possible basis choices, including the Fourier basis where 'w' represents the nth root of unity, and the quality of the basis depends on how well it captures the general smoothness of images.



![B = [ b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 ] where b0, b1,.., b7 are 8 x 1 linearly independent vectors.](https://image.slidesharecdn.com/imagecompression-110518050905-phpapp01/85/Image-compression-4-320.jpg)





