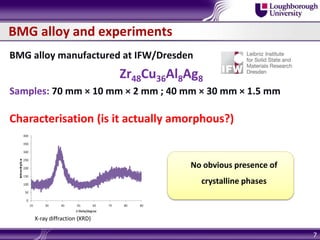
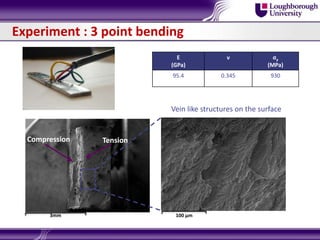
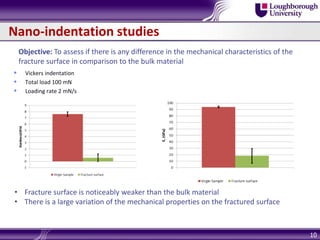
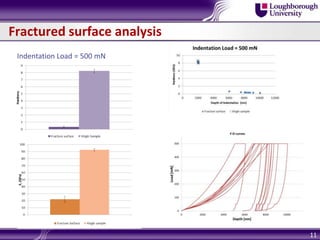
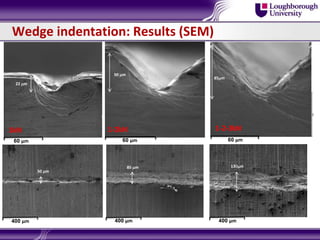
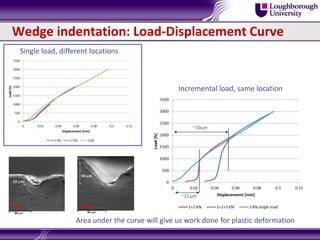
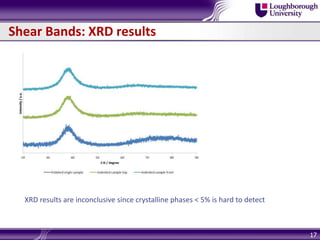
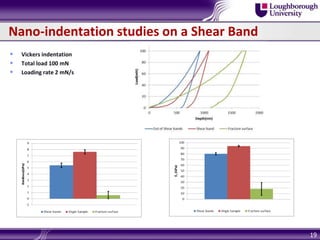
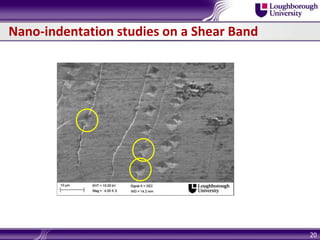
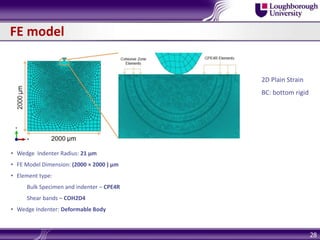
Bulk metallic glasses (BMGs) are amorphous alloys that can be formed into bulk samples rather than just thin films. This document discusses BMGs and characterizes a Zr-based BMG alloy. It describes experiments using 3-point bending and wedge indentation to study shear band formation. Wedge indentation showed vein-like structures and shear bands initiating and propagating with increasing load. Nanoindentation found fracture surfaces weaker than the bulk. Finite element modeling used cohesive zone elements to simulate shear band propagation. Future work includes gradient plasticity modeling of nucleation and shear band effects.

1. VAHID NEKOUIE
GAYAN ABEYGUNAWARDANE-ARACHCHIGE
ANISH ROY
VADIM SILBERSCHMIDT
1
Mechanics of Advanced
Materials Research Group

2. What is a Bulk Metallic Glass?
2
• amorphous material: atoms “frozen” in non-crystalline form
• first formed in 1957 by Duwez by rapid quenching
 gold-silicon alloy
 only very thin, small samples could be produced (order or micrometers)
• first believed atoms were randomly packed together densely like hard spheres
in a liquid
 solvent atoms randomly arranged with solute atoms fitting into open cavities
• now believe short-range, even medium-range order exists in materials
Sheng et al. (2006), Nature

3. What is a Bulk Metallic Glass?
3
BMG
Compared to metals in general, BMGs
have high strength, f and low
stiffness, E
Unusually high Elastic Strain, f/E
From: Material selection in mechanical design, MF Ashby (1999)
Very high Elastic stored energy

4. Applications
4
Digital light processor, hinges
made of Ti-Al metallic glass with
no fatigue failure after 1012 cycles.
Micro components in
MEMS devices
LENGTH SCALES

5. Introduction & Motivation
 Deformation mechanisms of metallic glass are unique
 plastic shear flow in the micro scale, but brittle fracture in macro scale
 At ambient temperatures/high stress: flow localization in shear bands (SB)
 At high temperatures/low stress: homogeneous viscous flow
Research Objectives
 Experiments: study SB initiation and evolution under loads. Characterise SBs
mechanically.
 Modelling: Develop a continuum model of SB initiation and propagation,
which can then be used to study component deformations across length
scales
5

6. What is a Shear band?
 Localised thin bands (~ 10 - 20 nm).
 Cohesion is maintained across the planes.
 Propagation is inhomogeneous
 Propagation depends on loading conditions, sample imperfection.
 Origin of SB is controversial: structural change? Temperature rise? Localised melting?
6
Source – nature materials

7. BMG alloy and experiments
BMG alloy manufactured at IFW/Dresden
Zr48Cu36Al8Ag8
Samples: 70 mm × 10 mm × 2 mm ; 40 mm × 30 mm × 1.5 mm
7
Characterisation (is it actually amorphous?)
X-ray diffraction (XRD)
No obvious presence of
crystalline phases

8. Experiment : 3 point bending
E
(GPa)
ν σy
(MPa)
95.4 0.345 930
3mm
TensionCompression
100 µm
Vein like structures on the surface

9. Experiment : 3 point bending
E
(GPa)
ν σy
(MPa)
95.4 0.345 930
400 µm
10 µm
Shear Bands are evident

10. Nano-indentation studies
10
• Fracture surface is noticeably weaker than the bulk material
• There is a large variation of the mechanical properties on the fractured surface
Objective: To assess if there is any difference in the mechanical characteristics of the
fracture surface in comparison to the bulk material
 Vickers indentation
 Total load 100 mN
 Loading rate 2 mN/s

11. Fractured surface analysis
11
Indentation Load = 500 mN

12. Wedge indentation studies
Why wedge?
Observing shear bands in Nano/Microindentation is difficult
o Shear bands initial in the material volume
o Bonded interface method is not ideal
With a Wedge we have a 2D plane-strain scenario
 Observe shear bands terminating on the surface as they initiation and evolve.
 Relatively easy to setup
 Easy to model
12

13. 1. Sample cut and polished
2. Loaded into a custom rig
Wedge indentation: Experimental steps
13
Zygo Talisurf
Ra = 2 to 3 nm
BMG Spring

14. Wedge indentation: details
Incremental loading: 1 KN to 3 KN
Deformation mode: Compression
Displacement rate: 0.5 mm/min
Indenter: HSS
14
60 µm
1kN
22 m
400 µm
50 m

15. Wedge indentation: Results (SEM)
60 µm
1kN
22 m
1-2kN
60 µm
50 m
1-2-3kN
60 µm
85m
400 µm 400 µm 400 µm
85 m 130m
50 m

16. Wedge indentation: Load-Displacement Curve
Single load, different locations
Incremental load, same location
~ 50µm
~22 µm
Area under the curve will give us work done for plastic deformation

17. Shear Bands: XRD results
17
XRD results are inconclusive since crystalline phases < 5% is hard to detect

18. Shear Band analysis/ TEM + SAED
18
Virgin Sample Shear Band
Crystalline material
FIB
milling
TEM/SAED sample
Shear Bands are fully
amorphous

19. Nano-indentation studies on a Shear Band
 Vickers indentation
 Total load 100 mN
 Loading rate 2 mN/s
19

20. Nano-indentation studies on a Shear Band
20

21. MODELLING OF WEDGE INDENTATION
/Finite Element Modelling
21

22. Microscale modelling – Bulk material
 Drucker – Prager : hydrostatic stress component is considered.
 Captures the rise of shear strength with the increase of hydrostatic pressure
increase. – Major cause for adoption.
𝐹 = 𝐽2 − 𝜃𝐼1 − 𝑘
J2 – second deviatoric stress invariant 𝜃 – constant for a given material
I1 – first stress invariant 𝑘 – hardening and softening function
ABAQUS 6.12 is used to model
Linear Drucker - Prager criterion is used:
𝒇 = 𝒕 − 𝒑𝒕𝒂𝒏𝜷 − 𝒅 Here: 𝜷 = 𝒇𝒓𝒊𝒄𝒕𝒊𝒐𝒏 𝒂𝒏𝒈𝒍𝒆 and 𝒅 = 𝒄𝒐𝒉𝒆𝒔𝒊𝒐𝒏 𝒑𝒂𝒓𝒂𝒎𝒆𝒕𝒆𝒓
To calculate, 𝒕 and 𝒅: 𝑡 =
1
2
q 1 +
1
𝑘
− 1 −
1
𝑘
𝑟
𝑞
3
and 𝑑 = 1 −
1
3
𝑡𝑎𝑛𝛽 𝜎𝑐
𝑞 = 𝑣𝑜𝑛 𝑚𝑖𝑠𝑒𝑠 𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑎𝑛𝑡 𝑠𝑡𝑟𝑒𝑠𝑠, 𝑘 = 𝑟𝑎𝑡𝑖𝑜 𝑜𝑓 𝑦𝑖𝑒𝑙𝑑 𝑠𝑡𝑟𝑒𝑠𝑠 𝑖𝑛 𝑡𝑟𝑖𝑎𝑥𝑖𝑎𝑙 𝑠𝑡𝑎𝑡𝑒
𝑟 = 𝑡ℎ𝑖𝑟𝑑 𝑖𝑛𝑣𝑎𝑟𝑖𝑎𝑛𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑑𝑒𝑣𝑖𝑎𝑡𝑜𝑟𝑖𝑐 𝑠𝑡𝑟𝑒𝑠𝑠
22

23. Microscale modelling – Shear band
 Cohesive Zone Elements with traction separation law.
 Shear band thickness lies in the ~nm scale. This fact prompt to employ
traction separation laws.
23
Linear elastic behaviour
𝜀 𝑛 =
𝛿 𝑛
𝑇0
, 𝜀 𝑠 =
𝛿 𝑠
𝑇0
, 𝜀𝑡 =
𝛿 𝑡
𝑇0
Traction – Separation response
Damage initiation criterion
𝜀 𝑛
𝜀 𝑛
0
2
+
𝜀 𝑠
𝜀 𝑠
𝑜
2
+
𝜀𝑡
𝜀𝑡
𝑜
2
= 1
Nominator calculated by the solver,
Denominator is user input dependent.
Linear damage evolution
𝐷 =
𝛿 𝑚
𝑓
𝛿 𝑚
𝑚𝑎𝑥−𝛿 𝑚
0
𝛿 𝑚
𝑚𝑎𝑥 𝛿 𝑚
𝑓
−𝛿 𝑚
0
𝛿 𝑚
𝑓
− effective displacement at complete failure,
𝛿 𝑚
0
− effective displacement at damage initiation
𝛿 𝑚
𝑓
− effective traction at damage initiation,
𝛿 𝑚
𝑚𝑎𝑥
− maximum value of the effective displacement

24. 24
• Wedge Indenter Radius: 20 μm
• FE Model Dimension: (2000 × 2000 ) µm
• Element type:
Bulk Specimen and indenter – CPE4R
Shear bands – COH2D4
• Wedge Indenter: Deformable Body
FE model
2D Plain Strain
BC: bottom rigid

25. 25
FE model – Material Properties
Drucker-Prager parameters
Hardening
Angle of
friction(β)
Flow stress
ratio
Dilation angle (ψ)
0.01° 1 0.02°
Shear damage parameters
Yield stress (MPa) Plastic strain
Fracture
strain
Shear stress
ratio
Strain rate ( s-1 )
930 0
0.05 1 0.016
• Material Properties for bulk metallic glass –
E (GPa) ν
95.4 0.345
• Material Properties for deformable indenter (HSS)–
E (GPa) ν
231 0.30
• Material properties for CZE were chosen by sensitivity analysis.

26. 26
FE model: Results
Damage initiation and propagation through the shear band

27. Outlook & Future Work
 SB and Fracture surface are weaker than bulk material
 SB are amorphous … rules out melting
 Cohesive Zone Elements can be used to determined the
propagation along the shear band.
 A gradient plasticity based approach is currently being developed
to capture the nucleation and the effect of the local shear bands.
27

28. 28
• Wedge Indenter Radius: 21 μm
• FE Model Dimension: (2000 × 2000 ) µm
• Element type:
Bulk Specimen and indenter – CPE4R
Shear bands – COH2D4
• Wedge Indenter: Deformable Body
FE model
2D Plain Strain
BC: bottom rigid