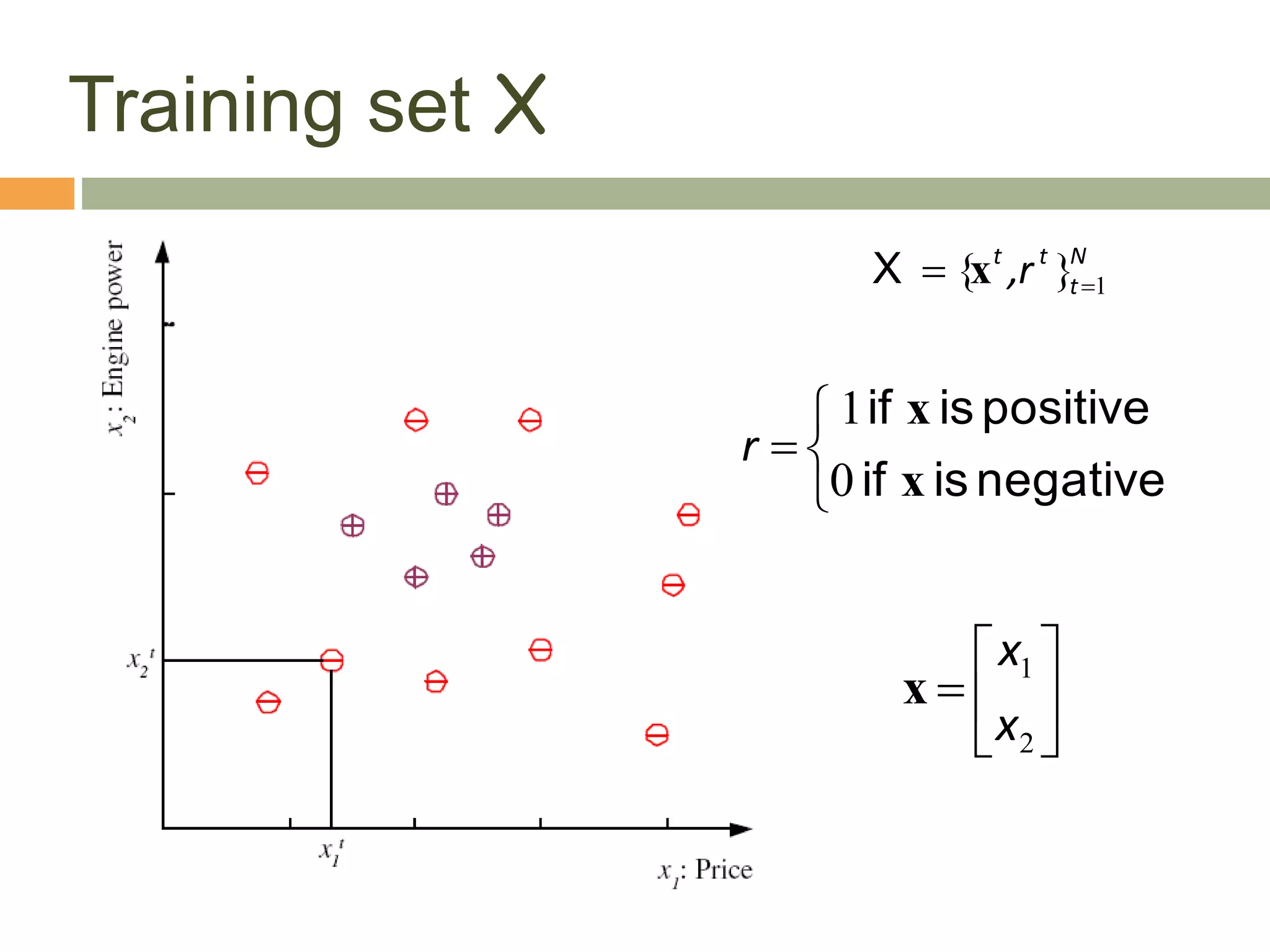
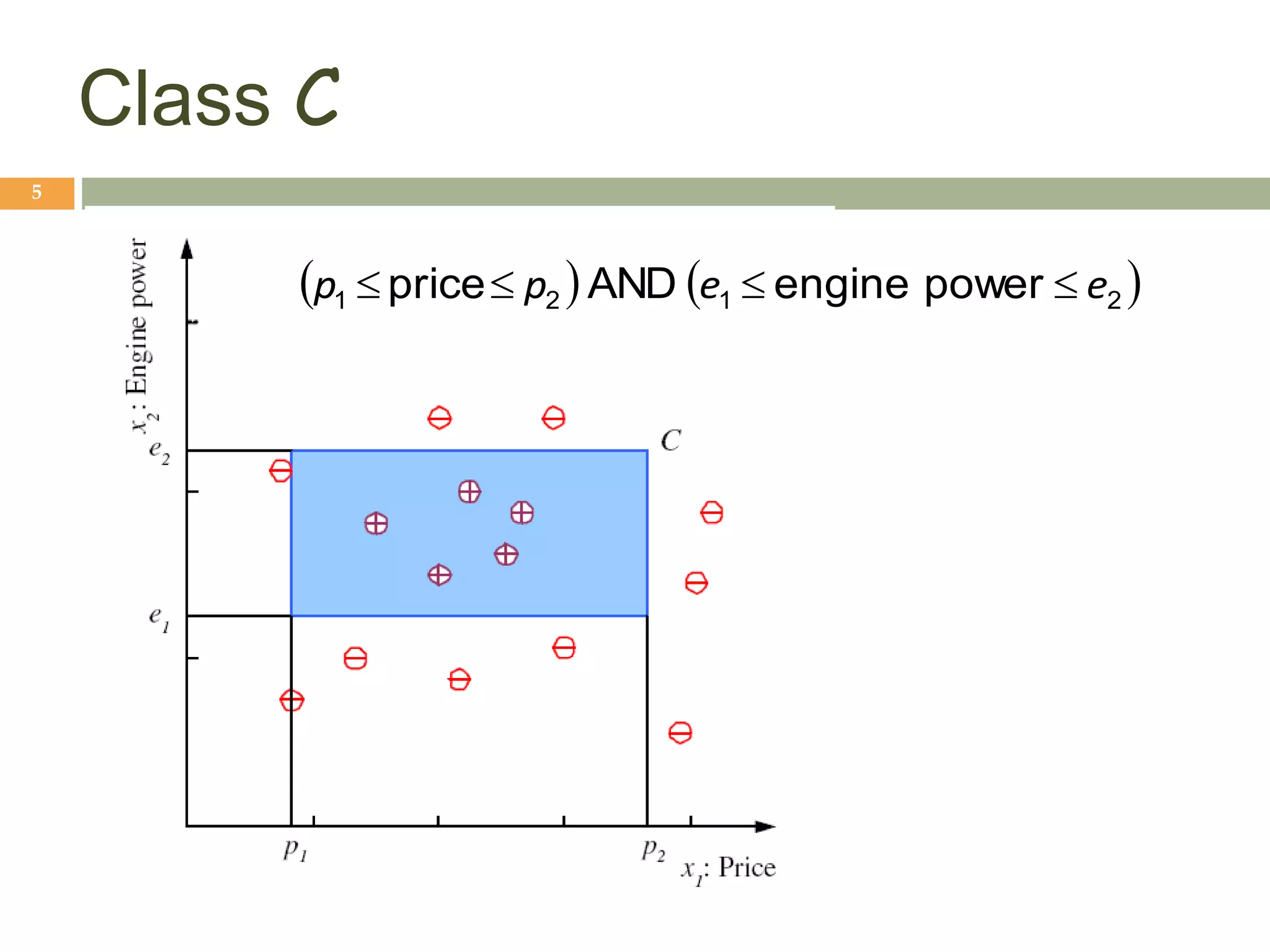
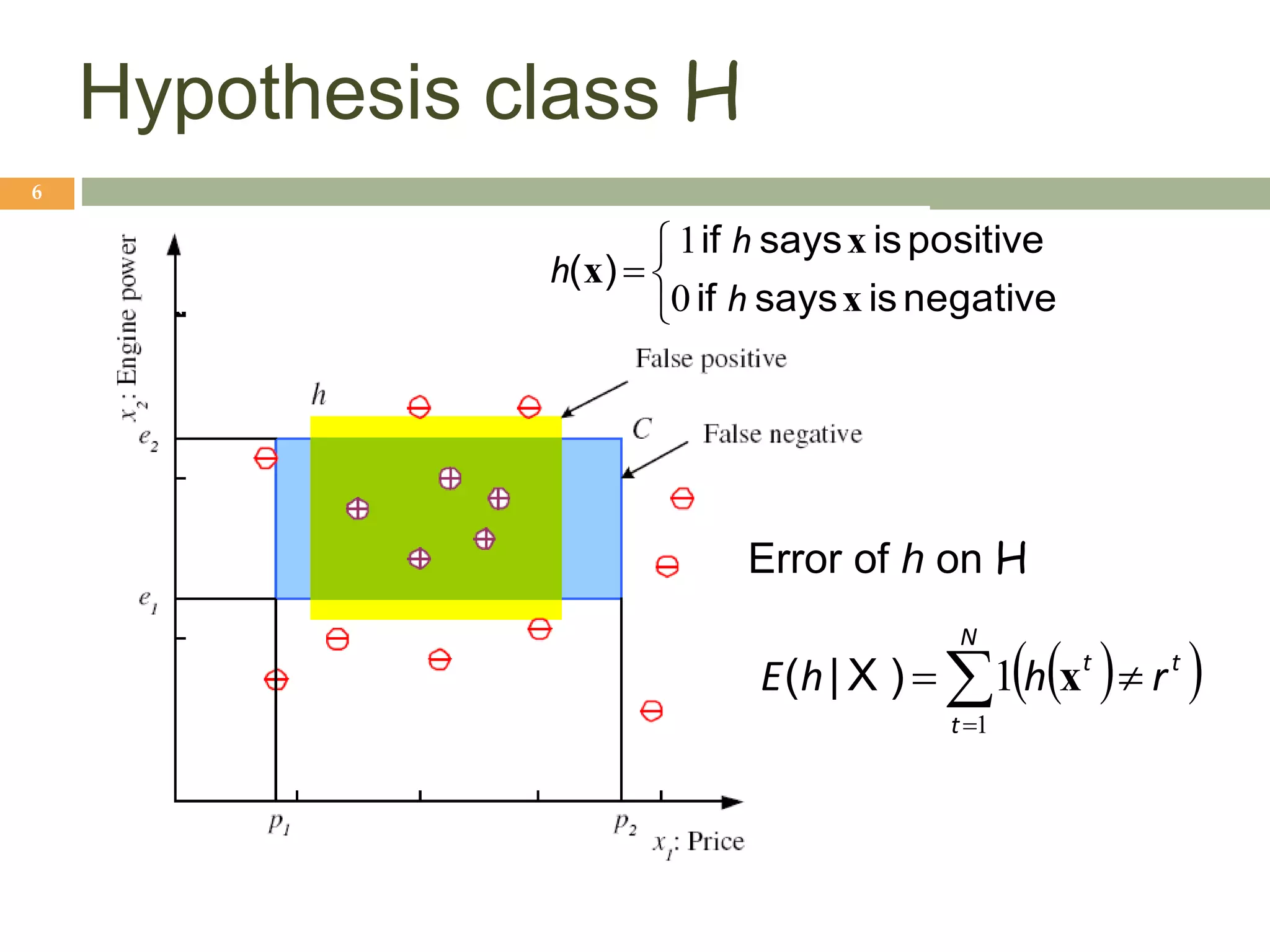
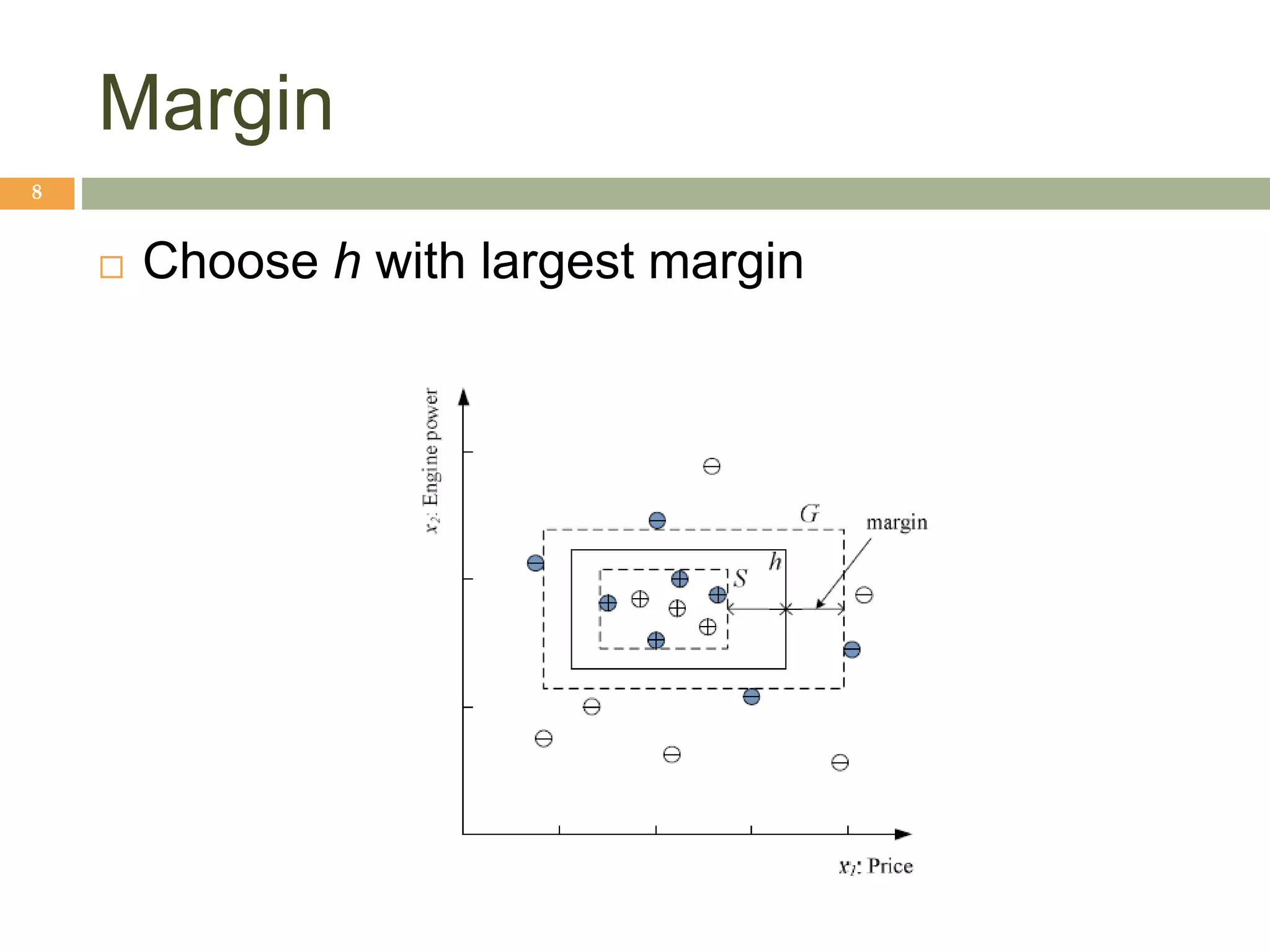
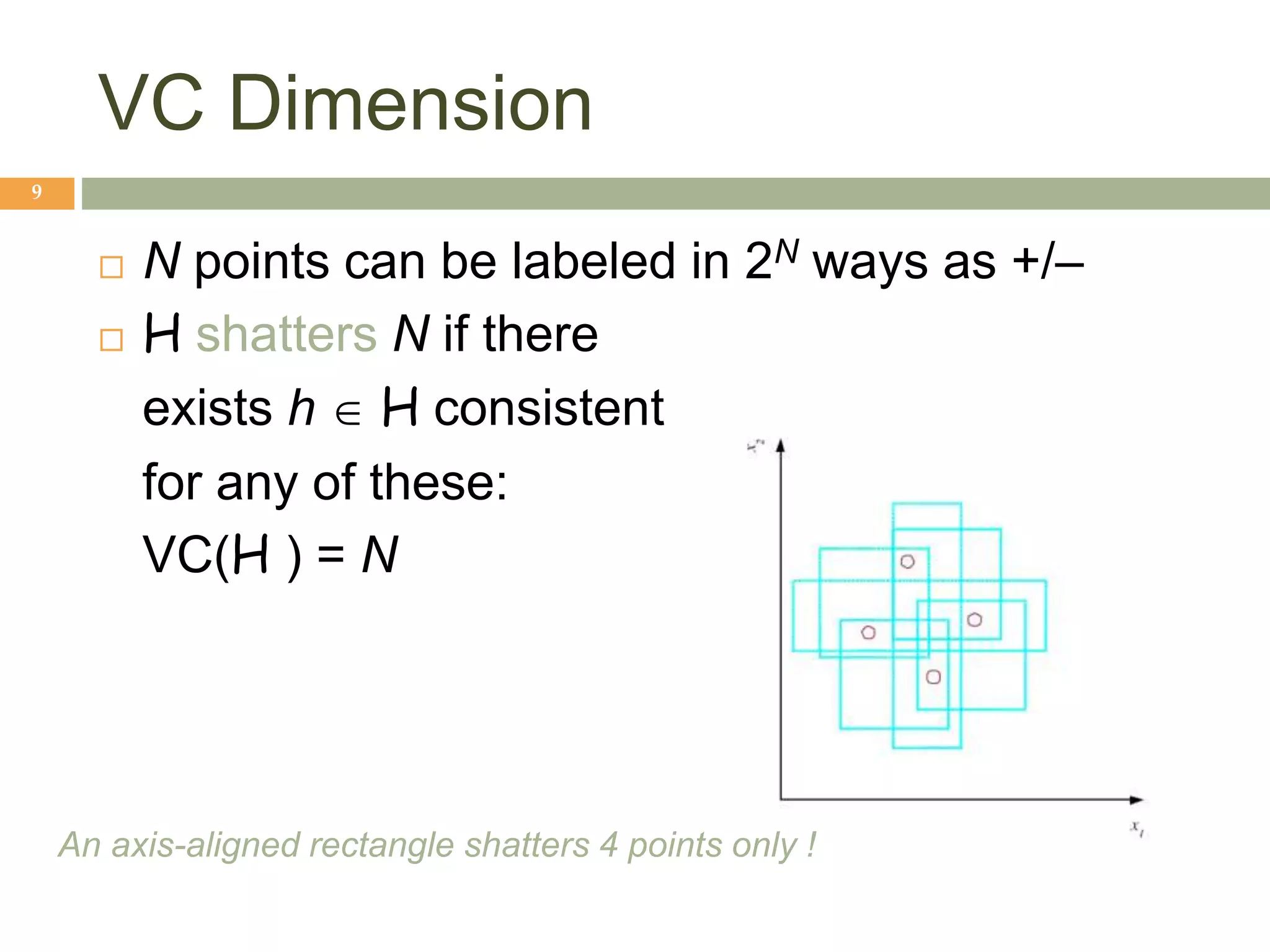
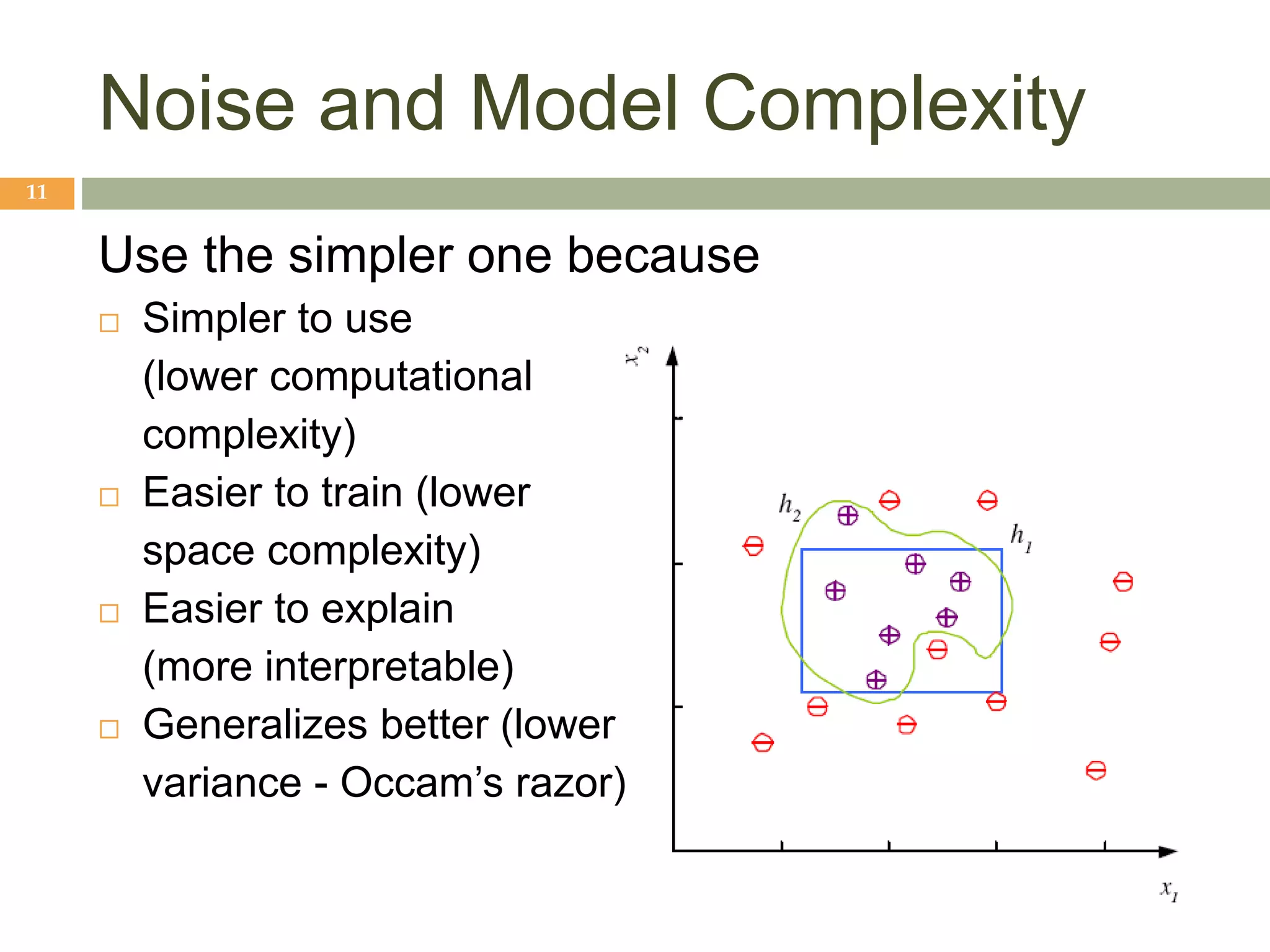
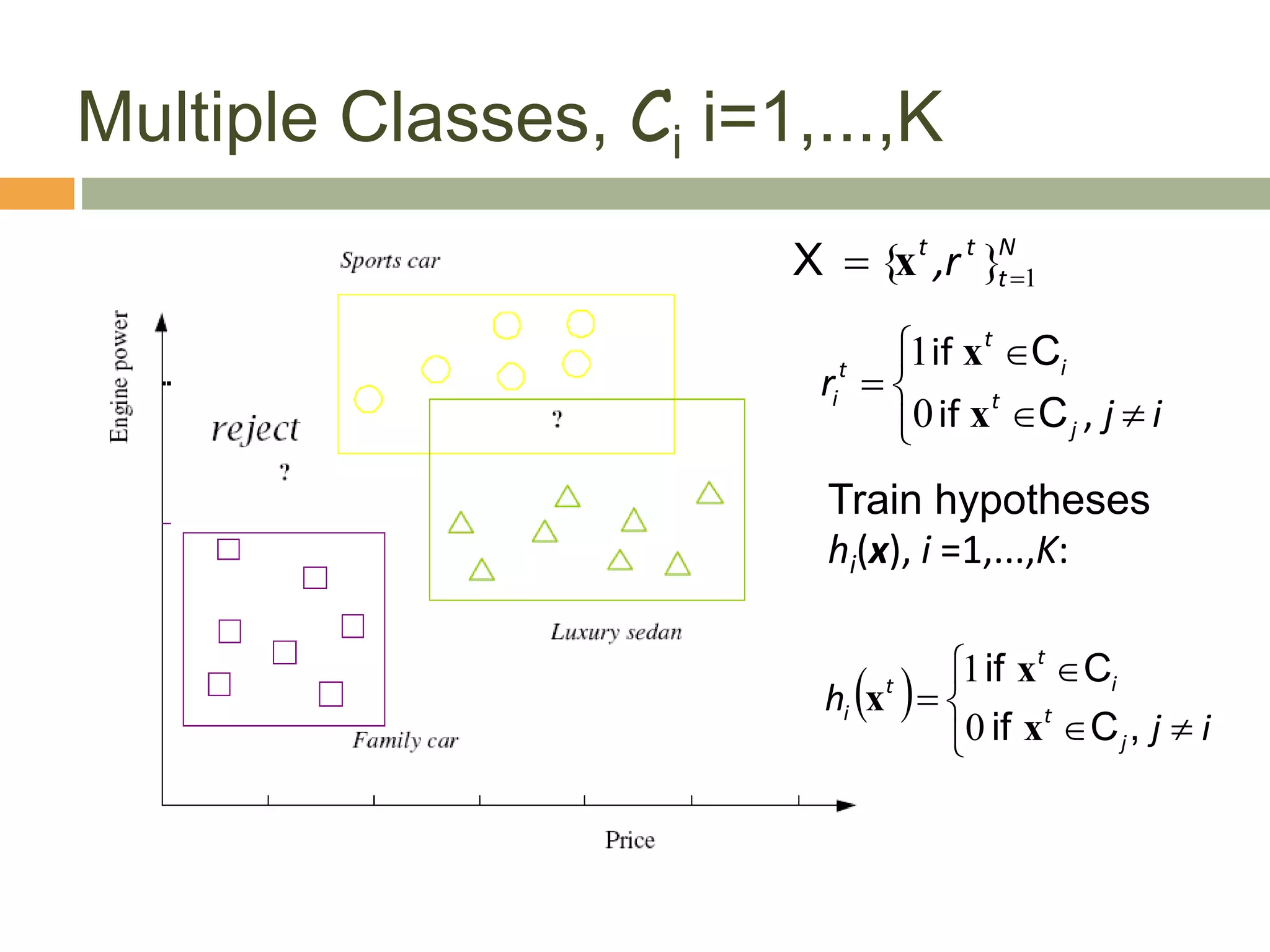
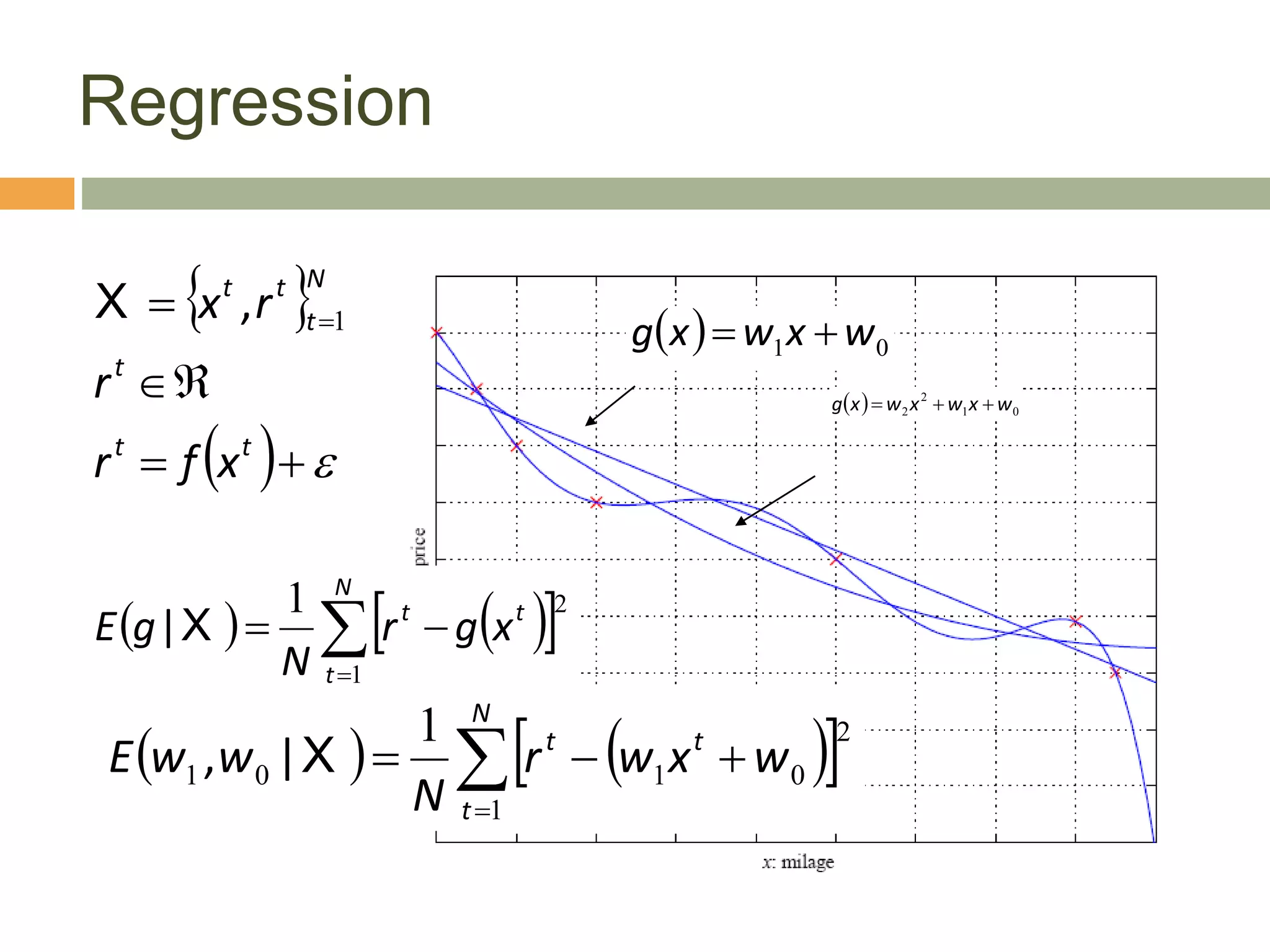
This document provides an introduction to machine learning and supervised learning. It discusses key concepts like training examples, hypotheses, error, model complexity, and overfitting. The goal of supervised learning is to learn a function that maps inputs to outputs from example input-output pairs. Choosing the right model complexity involves balancing training error, generalization error, and model interpretability.

1. INTRODUCTION
TO
MACHINE
LEARNING
3RD EDITION
ETHEM ALPAYDIN
© The MIT Press, 2014
alpaydin@boun.edu.tr
http://www.cmpe.boun.edu.tr/~ethem/i2ml3e
Lecture Slides for

2. CHAPTER 2:
SUPERVISED
LEARNING

3. Learning a Class from
Examples
3
 Class C of a “family car”
 Prediction: Is car x a family car?
 Knowledge extraction: What do people expect from a
family car?
 Output:
Positive (+) and negative (–) examples
 Input representation:
x1: price, x2 : engine power

4. Training set X
N
t
t
t
,r 1
}
{ 
 x
X




negative
is
if
positive
is
if
x
x
0
1
r
4







2
1
x
x
x

5. Class C
5
   
2
1
2
1 power
engine
AND
price e
e
p
p 




6. Hypothesis class H




negative
is
says
if
positive
is
says
if
)
(
x
x
x
h
h
h
0
1
 
 




N
t
t
t
r
h
h
E
1
1 x
)
|
( X
6
Error of h on H

7. S, G, and the Version Space
7
most specific hypothesis, S
most general hypothesis, G
h H, between S and G is
consistent and make up the
version space
(Mitchell, 1997)

8. Margin
8
 Choose h with largest margin

9. VC Dimension
9
 N points can be labeled in 2N ways as +/–
 H shatters N if there
exists h  H consistent
for any of these:
VC(H ) = N
An axis-aligned rectangle shatters 4 points only !

10. Probably Approximately Correct
(PAC) Learning
10
 How many training examples N should we have, such that with
probability at least 1 ‒ δ, h has error at most ε ?
(Blumer et al., 1989)
 Each strip is at most ε/4
 Pr that we miss a strip 1‒ ε/4
 Pr that N instances miss a strip (1 ‒ ε/4)N
 Pr that N instances miss 4 strips 4(1 ‒ ε/4)N
 4(1 ‒ ε/4)N ≤ δ and (1 ‒ x)≤exp( ‒ x)
 4exp(‒ εN/4) ≤ δ and N ≥ (4/ε)log(4/δ)

11. Noise and Model Complexity
11
Use the simpler one because
 Simpler to use
(lower computational
complexity)
 Easier to train (lower
space complexity)
 Easier to explain
(more interpretable)
 Generalizes better (lower
variance - Occam’s razor)

12. Multiple Classes, Ci i=1,...,K
N
t
t
t
,r 1
}
{ 
 x
X







,
if
if
i
j
r
j
t
i
t
t
i
C
C
x
x
0
1
 







,
if
if
i
j
h
j
t
i
t
t
i
C
C
x
x
x
0
1
12
Train hypotheses
hi(x), i =1,...,K:

13. Regression
  0
1 w
x
w
x
g 

  0
1
2
2 w
x
w
x
w
x
g 


   
 




N
t
t
t
x
g
r
N
g
E
1
2
1
X
|
13
   
 





N
t
t
t
w
x
w
r
N
w
w
E
1
2
0
1
0
1
1
X
|
,
 
  




 
t
t
t
N
t
t
t
x
f
r
r
r
x 1
,
X

14. Model Selection &
Generalization
14
 Learning is an ill-posed problem; data is not
sufficient to find a unique solution
 The need for inductive bias, assumptions
about H
 Generalization: How well a model performs on
new data
 Overfitting: H more complex than C or f
 Underfitting: H less complex than C or f

15. Triple Trade-Off
15
 There is a trade-off between three factors
(Dietterich, 2003):
1. Complexity of H, c (H),
2. Training set size, N,
3. Generalization error, E, on new data
 As N,E
 As c (H),first Eand then E

16. Cross-Validation
16
 To estimate generalization error, we need data
unseen during training. We split the data as
 Training set (50%)
 Validation set (25%)
 Test (publication) set (25%)
 Resampling when there is few data

17. Dimensions of a Supervised
Learner
1. Model:
2. Loss function:
3. Optimization procedure:
 

|
x
g
   
 


t
t
t
g
r
L
E 
 |
,
| x
X
17
 
X
|
min
arg
* 


E
