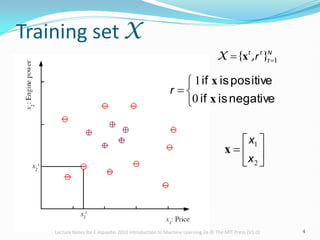
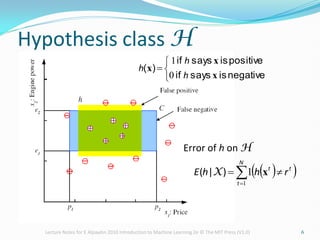
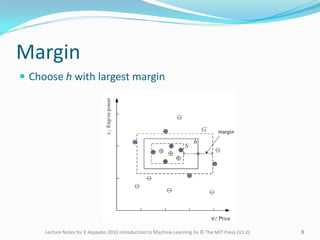
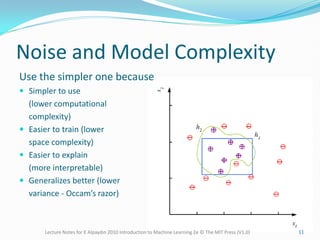
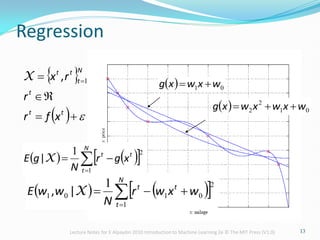
The document provides lecture notes on machine learning concepts, covering topics such as hypothesis classes, training examples, model complexity, and the importance of generalization. It discusses methods for estimating generalization error, such as cross-validation, and highlights the trade-offs between complexity, training set size, and error rates. Additionally, it addresses the concept of PAC learning and the need for inductive bias in the learning process.

1. ETHEM ALPAYDIN
© The MIT Press, 2010
alpaydin@boun.edu.tr
http://www.cmpe.boun.edu.tr/~ethem/i2ml2e
Lecture Slides for

3. Learning a Class from Examples
 Class C of a “family car”
 Prediction: Is car x a family car?
 Knowledge extraction: What do people expect from a
family car?
 Output:
Positive (+) and negative (–) examples
 Input representation:
x1: price, x2 : engine power
3
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

4. Training set X
N
t
t
t
,r 1
}
{ 
 x
X




negative
is
if
positive
is
if
x
x
0
1
r
4







2
1
x
x
x
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

5. Class C
   
2
1
2
1 power
engine
AND
price e
e
p
p 



5
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

6. Hypothesis class H




negative
is
says
if
positive
is
says
if
)
(
x
x
x
h
h
h
0
1
 
 




N
t
t
t
r
h
h
E
1
1 x
)
|
( X
6
Error of h on H
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

7. S, G, and the Version Space
7
most specific hypothesis, S
most general hypothesis, G
h H, between S and G is
consistent
and make up the
version space
(Mitchell, 1997)
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

8. Margin
 Choose h with largest margin
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0) 8

9. VC Dimension
 N points can be labeled in 2N ways as +/–
 H shatters N if there
exists h  H consistent
for any of these:
VC(H ) = N
9
An axis-aligned rectangle shatters 4 points only !
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

10. Probably Approximately Correct
(PAC) Learning
 How many training examples N should we have, such that with probability
at least 1 ‒ δ, h has error at most ε ?
(Blumer et al., 1989)
 Each strip is at most ε/4
 Pr that we miss a strip 1‒ ε/4
 Pr that N instances miss a strip (1 ‒ ε/4)N
 Pr that N instances miss 4 strips 4(1 ‒ ε/4)N
 4(1 ‒ ε/4)N ≤ δ and (1 ‒ x)≤exp( ‒ x)
 4exp(‒ εN/4) ≤ δ and N ≥ (4/ε)log(4/δ)
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0) 10

11. Noise and Model Complexity
Use the simpler one because
 Simpler to use
(lower computational
complexity)
 Easier to train (lower
space complexity)
 Easier to explain
(more interpretable)
 Generalizes better (lower
variance - Occam’s razor)
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0) 11

12. Multiple Classes, Ci i=1,...,K
N
t
t
t
,r 1
}
{ 
 x
X







,
if
if
i
j
r
j
t
i
t
t
i
C
C
x
x
0
1
 







,
if
if
i
j
h
j
t
i
t
t
i
C
C
x
x
x
0
1
12
Train hypotheses
hi(x), i =1,...,K:
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

13. Regression
  0
1 w
x
w
x
g 

  0
1
2
2 w
x
w
x
w
x
g 


   
 




N
t
t
t
x
g
r
N
g
E
1
2
1
X
|
13
   
 





N
t
t
t
w
x
w
r
N
w
w
E
1
2
0
1
0
1
1
X
|
,
 
  




 
t
t
t
N
t
t
t
x
f
r
r
r
x 1
,
X
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)

14. Model Selection & Generalization
 Learning is an ill-posed problem; data is not sufficient to
find a unique solution
 The need for inductive bias, assumptions about H
 Generalization: How well a model performs on new data
 Overfitting: H more complex than C or f
 Underfitting: H less complex than C or f
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0) 14

15. Triple Trade-Off
 There is a trade-off between three factors (Dietterich,
2003):
1. Complexity of H, c (H),
2. Training set size, N,
3. Generalization error, E, on new data
 As NE
 As c (H)first Eand then E
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0) 15

16. Cross-Validation
 To estimate generalization error, we need data unseen
during training. We split the data as
 Training set (50%)
 Validation set (25%)
 Test (publication) set (25%)
 Resampling when there is few data
Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0) 16

17. Dimensions of a Supervised
Learner
1. Model:
2. Loss function:
3. Optimization procedure:
 

|
x
g
   
 


t
t
t
g
r
L
E 
 |
,
| x
X
17
 
X
|
min
arg
* 


E

Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2e © The MIT Press (V1.0)