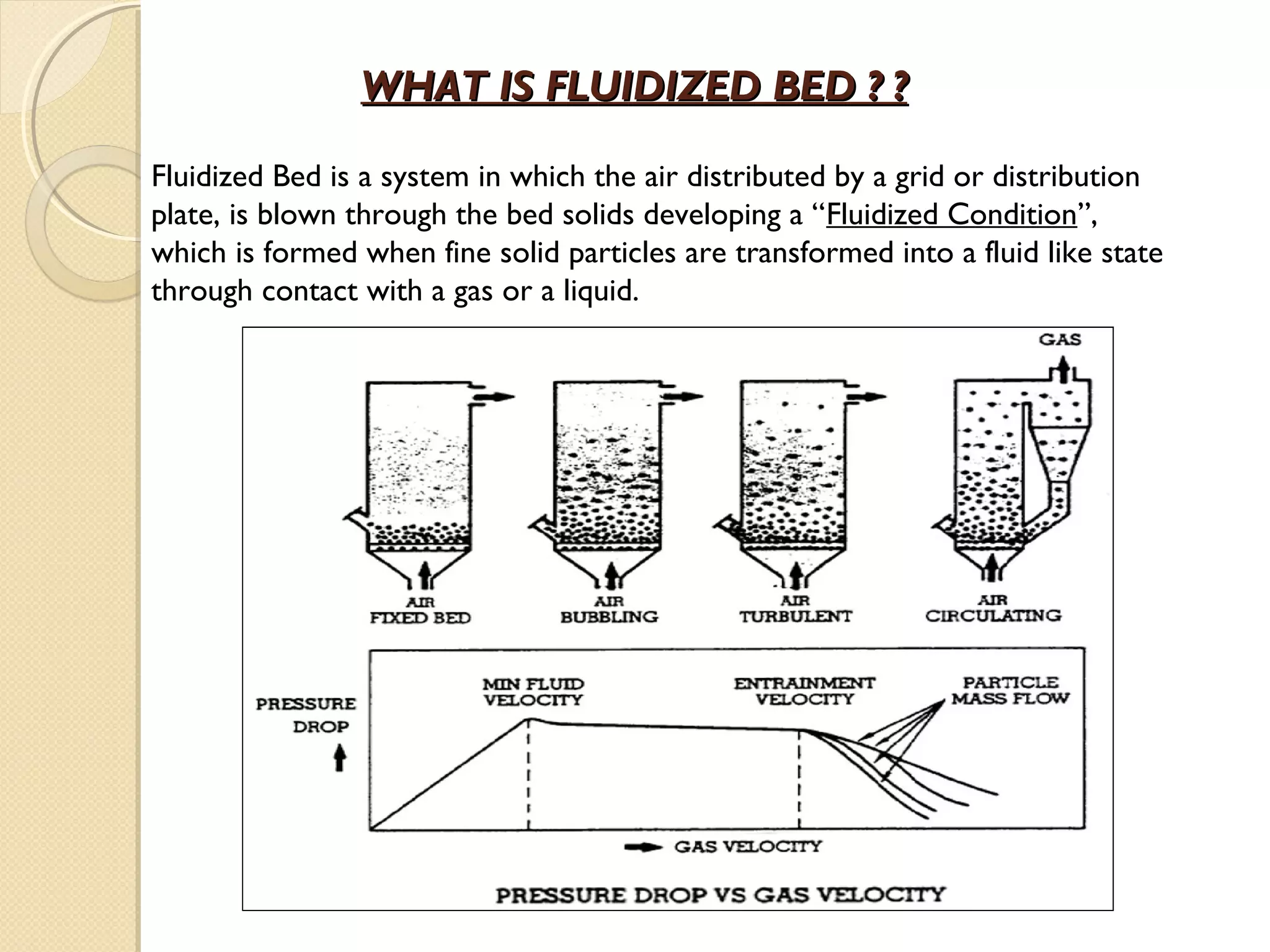
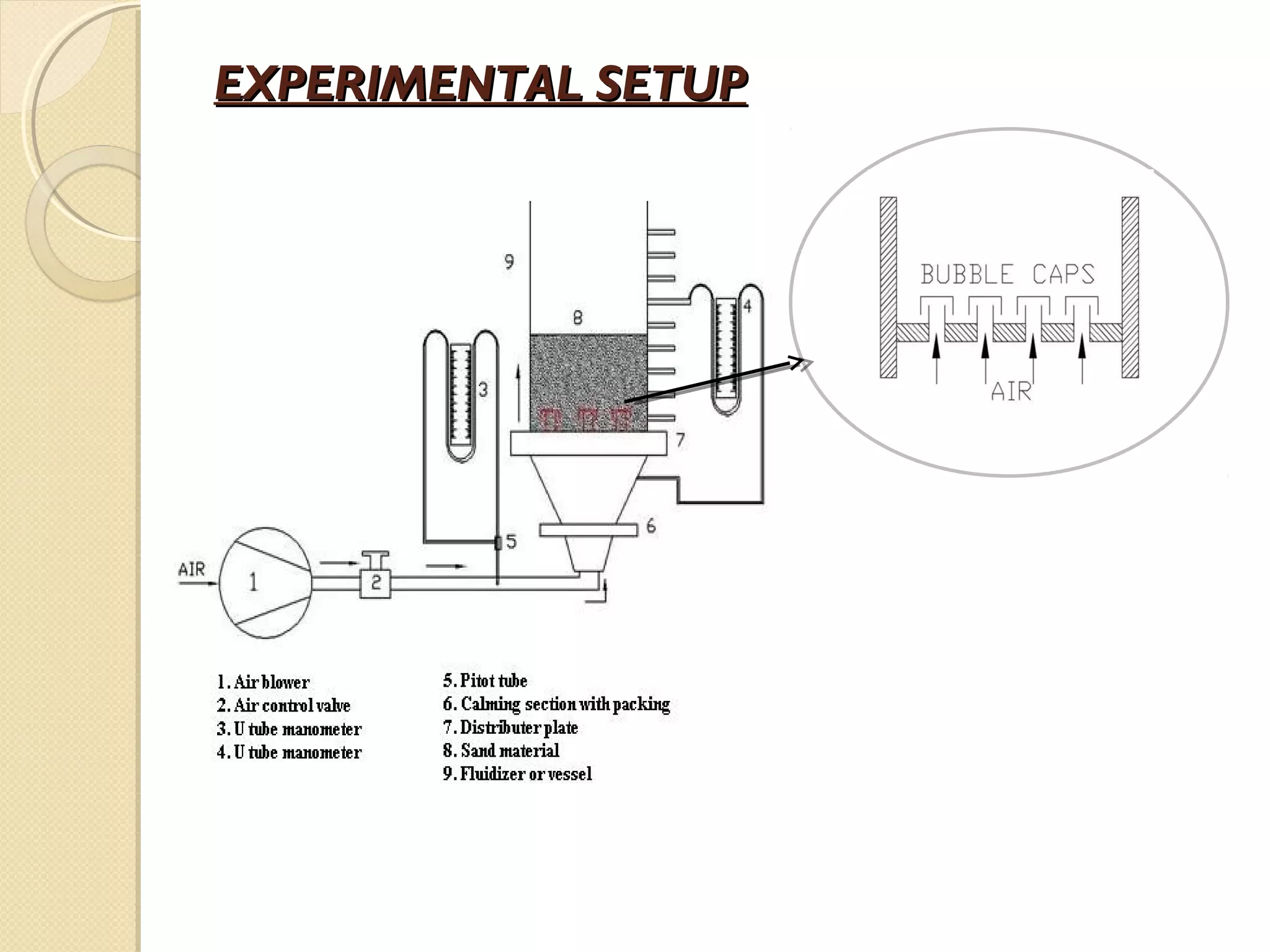
This document summarizes a study on the hydrodynamic behavior of a cold model bubbling fluidized bed system using bubble caps. Key findings include: 1) Experiments were conducted on a laboratory scale cold model fluidized bed system to study hydrodynamic parameters like minimum fluidization velocity (Umf) and terminal velocity (Ut) that are difficult to measure under actual high temperature/pressure conditions. 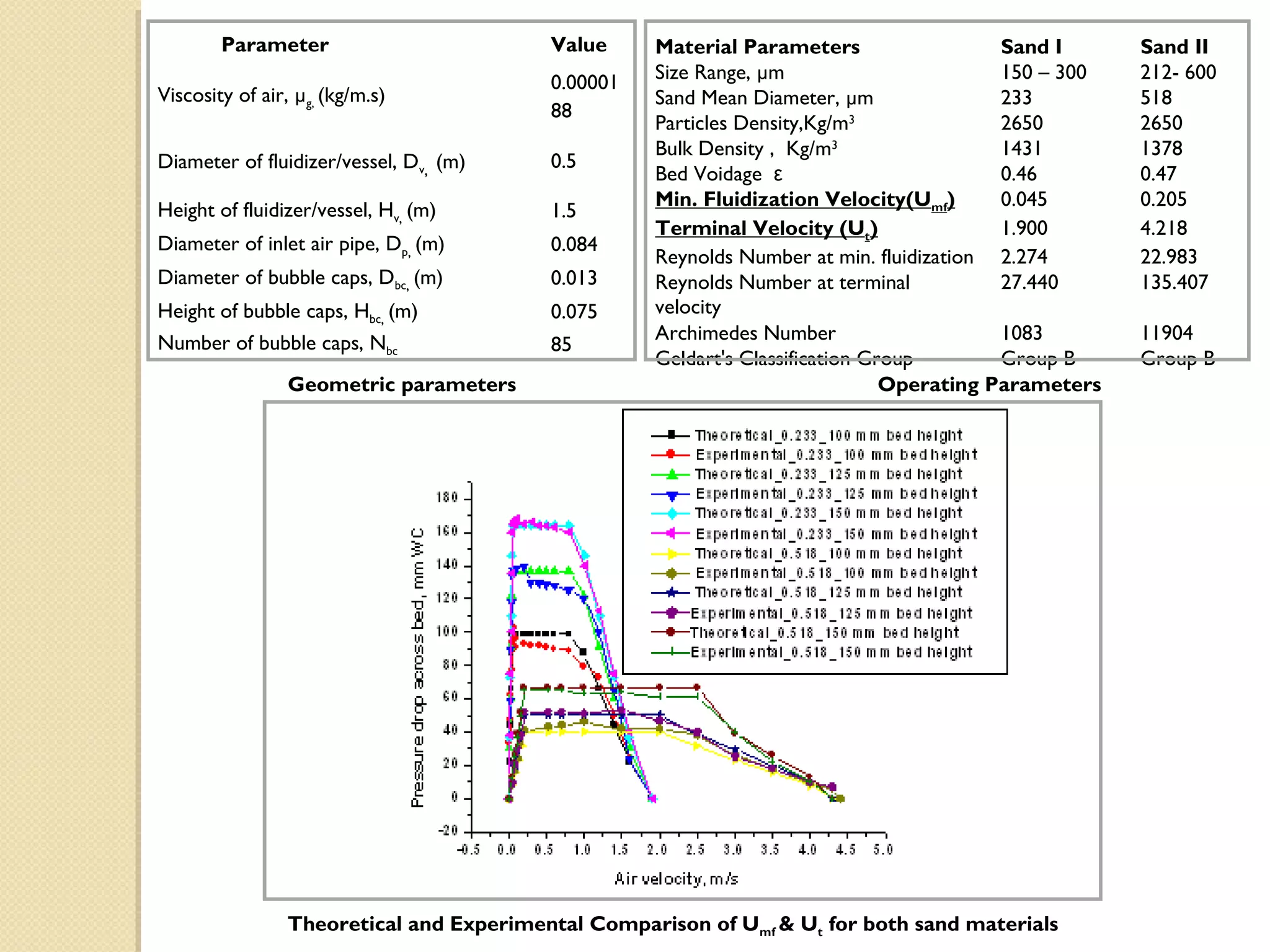2) Parameters measured included Umf, Ut, and bubble behavior for two types of sand (Sand I and Sand II) used as bed material. Theoretical predictions of Umf and Ut using established equations were also compared to experimental values. 3) Results provide insights into the fundamental hydrodynamics of

1. Hydrodynamic Study of Cold Model
Bubbling Fluidized Bed System Using
Bubble Caps
By
Mandeep Sharma Dinanath Akela
(Project Assistant, CMERI Durgapur) (Engineer, THERMAX Pune)
Central Mechanical Engineering Research Institute, Durgapur 713209, West Bengal, India

2. WHAT IS FLUIDIZED BED ? ?
Fluidized Bed is a system in which the air distributed by a grid or distribution
plate, is blown through the bed solids developing a “Fluidized Condition”,
which is formed when fine solid particles are transformed into a fluid like state
through contact with a gas or a liquid.

3. CHARACTERISTICS OF FLUIDIZED BED
Fluidized beds display a number of liquid-like properties:
 Lighter objects float on top of the bed (i.e., objects less dense than the bulk density
of the bed),
 The surface stays horizontal even in tilted beds,
 The solids can flow through an opening in the vessel just like a liquid,
 The beds have a “static” pressure head due to gravity, given by ρ0gh,
 Levels between two similar fluidized beds equalize their static pressure heads.
ADVANTAGES OF FLUIDIZED BED
 Rapid mixing of solids, uniform temperature and concentrations.
 Applicable for large or small scale operations.
 Heat and mass transfer rates between gas and particles are high as compared to
other modes of contacting.
 There is no moving part and hence a fluidized bed reactor is not mechanically agitated
reactor. So, maintenance cost can be low.
 The reactor is mounted vertically and save space.
APPLICATIONS
 Reactors for Cracking hydrocarbons, Coal gasification, Carbonization, Calcination.
 Heat exchangers, Drying operations, Coating (example, metals with polymer)
 Solidification/Granulation, Adsorption/desorption, Bio-fuel generation

4. Parameters Affecting Fluidization Behavior

5. CLASSIFICATION OF FBC TECHNOLOGY…

6. Bubbling Fluidized Bed
 Gas-solid bubbling fluidized bed (BFB) system is an efficient energy
conversion method for combustion and gasification of solid fuels.
 The combustion gas velocity is equal to “the minimum fluidization velocity”,
bubbles are gas voids with very little or no solids, the upward flow rate for
air/combustion gases is typically 2 - 3 m/s, the bed heights for BFBC plants
are 0.5 to 1.5 m, gas residence time within the bed are between 1 and 2
seconds.
 Chemical and thermal behavior of BFB combustors is greatly influenced
by the fundamental hydrodynamics of bed material, fluidizing medium
and bubble behavior.
 In actual BFB systems, it is very difficult to study these hydrodynamic
parameters due to very high temperature and pressure conditions.
Therefore, the objective of the present study is to investigate the
hydrodynamic parameters by conducting experiments on laboratory
scale BFB cold model at atmospheric conditions.

7. IMPORTANCE OF THE DISTRIBUTOR
Different type of distributors have different significances:
• With heavy load in large dia. beds, flat plates deflect unpredictably, hence
curved plates (c & d) are used. These withstand heavy loads and thermal
stresses well.
• Type f consists of slits between grate bars, has the same characteristics as
the flat perforated plate, but with a somewhat less uniform gas distribution.
• Nozzle (type g) and bubble caps (type h) are widely used to prevent solids
from falling through the distributor.

8. EXPERIMENTAL SETUP

9. Min. Fluidization Velocity
The pressure drop through fixed beds of has been correlated by Ergun[13] using the
equation: 2
∆P (1 − ε m ) 2 µ g uo 1 − ε m ρ g uo
g c = 150 + 1.75 3 ………………….. (1)
L 3
εm (φ s d p )
2
εm φsd p
The minimum fluidization occurs when
(drag force by upward moving gas ) = (weight of particles)
or (∆P bed) (Area bed) = (Volume bed) (Fraction of solids) (specific weight of solids)
 g 
or ∆P. Abed = ( Abed Lmf )(1 − ε mf ) ( ρ s − ρ g )  ………………….. (2)
 gc 
Umf , the superficial velocity of gas at minimum fluidization conditions, is found by
combining eqn. (1) and eqn.(2):
1.75  d p umf ρ g  150(1 − ε mf )  d p umf ρ g  d p ρ g ( ρ s − ρ g ) g
2 3

3 
 +  = ..........................(3)
φsε mf  µg   φs ε mf
2 3  µ  µg
2
 g 
The equation (3) can also be written as:
1
d p u mf ρ g  d p ρg (ρs − ρg )g 
3 2
= ( 33.7 ) + 0.0408
2
Re mf =  − 33.7 …………………..(4)
µg 
 µg
2



10. Terminal Velocity of Sand Particles
The gas flow rate through a fluidized bed is limited on one hand by u mf and on the other by entrainment of
solids by the gas. When entrainment occurs these solids must be recycled or replaced by fresh material to
maintain steady-state operations. This upper limit to the gas flow rate is approximated by the terminal or
free-fall velocity of the particles [14], which can be estimated from fluid mechanics by:
4 gd p ( ρs − ρg )  2
1
ut =   …..…(5)

 3ρg C d 

Where Cd is the experimentally determined drag coefficient.
10
C d , spherical = 12
, 0.4<Rep<500 …..…(6)
Re p
The expression for terminal velocity [14] is also given as
below:
( )
1
 4 ρ s − ρ g 2 d p2  2
U t , spherical =  d , 0.4<Rep<500 …..…(7)
 225 ρ gµ g  p
 
Terminal velocity(non-spherical),Ut’=Kt .Ut (spherical) ……... (8)
The correlation factor Kt is obtained by [15] :
 ϕ 
K t = 0.843 log 10   For Re <0.2, …... (9)
 0.065 
 4( ρp − ρg ) gd v 
0. 5
Kt =   For Re<1000, …... (10)
3ρg ( 5.31 −4.88 ϕ) 
 
Experimentally, terminal velocity of type sand I and sand II is find out by visual observations i.e. when the inlet air
flow rate is increased beyond the flow rate at which entrainment of sand particles is started, the pressure drop across
the bed is decreasing and at certain stage this pressure drop almost tend to zero when there is almost negligible sand
material in the bed. At this stage, terminal velocity for both sand materials is obtained.

11. Parameter Value Material Parameters Sand I Sand II
0.00001 Size Range, µm 150 – 300 212- 600
Viscosity of air, µg, (kg/m.s) Sand Mean Diameter, µm 233 518
88
Particles Density,Kg/m 3
2650 2650
Bulk Density , Kg/m 3
1431 1378
Diameter of fluidizer/vessel, Dv, (m) 0.5
Bed Voidage ε 0.46 0.47
Min. Fluidization Velocity(Umf) 0.045 0.205
Height of fluidizer/vessel, Hv, (m) 1.5
Terminal Velocity (Ut) 1.900 4.218
Diameter of inlet air pipe, Dp, (m) 0.084
Reynolds Number at min. fluidization 2.274 22.983
Diameter of bubble caps, Dbc, (m) 0.013 Reynolds Number at terminal 27.440 135.407
Height of bubble caps, Hbc, (m) 0.075 velocity
Number of bubble caps, Nbc Archimedes Number 1083 11904
85
Geldart's Classification Group Group B Group B
Geometric parameters Operating Parameters
Theoretical and Experimental Comparison of Umf & Ut for both sand materials

12. Bubble Behavior
A. Minimum Bubbling Velocity (Umb):
Fluidized systems with a small density difference between fluid and particles expand uniformly, while those
with a large density difference are generally unstable and produce bubbling. The lowest gas velocity at which
bubbling occurs is called the minimum bubbling velocity. There are two correlations are presented to find u mb:
1) The correlation to find umb is given by Broadhurst and Becker [16] :
 
 
d pU mb ρ g  Ar 
Re mb = = …………… (11)
µg  0.22 
 9.8 × 104 Ar − 0.82  ρ s  + 35.4 
 ρ 

  g 

2) Geldart[17] suggested a correlation for minimum bubbling velocity as:
U mb = K mb ×d p …………… (12)
Where Kmb is a constant whose value is 100 in cgs system. Davison & Harrison observed that the interval
between minimum bubbling velocity and minimum fluidization velocity represents the stable uniform
fluidization, which shrinks rapidly as the size of the particles increases.
B. Bubble size
There are several methods of observing bubbles in gas-solid fluidized beds:
1) Simple methods like visual observation if vessel is transparent,
2) still or cine photography,
3) using probes,
4) using two dimensional beds,
5) X-ray observation,
6) observation of particle movement,
7) observation of single isolated bubble.

13. The major advance in the study of fluid beds came with the investigations of single, isolated bubbles. The
Davison model remains useful as a first approximation. An isolated bubble in a fluid bed takes the form of an
indented sphere. The leading spherical surface is called the roof and the apex is the nose. The solids filling the
indentation are transported with the bubble for natural sand from 100 to 600 µm the wake fraction was from
0.22 to 0.28. The rise in velocity of an isolated bubble [18] depends on its size, given as:
1
U b = 0.79 gVb 2 = 0.711 gDb …………… (13)
C. Bubble growth and coalescence
After detachment from the distributor, bubbles interact as they rise in the bed. The coalescence of a pair of
bubbles has been investigated by Clift and Grace [19,20] and by Toei and Matsuno[21]. There are several
characteristics of the coalescence process. The leading bubble spreads horizontally as the trailing bubble
elongates and accelerates into the wake of the leader. The volume of two bubbles increases by 20-30%
during coalescence, followed by a 10% decrease during consolidation after wake entry, giving a net volume
increase of 10-20%. There is increased gas flow through the emulsion phase between the bubbles. The
following relation finds the maximum size:
( )
0. 4
 Dbed 2 U 0 − U mf 
D b∞ = 2.35  …………… (14)

 g

Bubble growth and splitting lead to a distribution of bubble size in the bed. Agarwal used a population balance to calculate the
bubble distribution. Three correlations have been found to be reliable for mean bubble size.
1) Mori & Wen [22] use the initial and maximum bubble sizes with first order growth rate (as it is the
most popular equation for calculation). With distributor plate having Bubble cap,
Db ( H ) = Db∞ − ( Db∞ − Db 0 ) exp  − 0.3H

.............(15)
 Dbed 


14. 2) Darton [23] has suggested another correlation for bubble size and the same is represented as:
0 .8
 
0.54(u −u mf ) Abed
0 .4
H + 4 
 N or 
Db ( H ) =   …………….. (16)
0 .2
g
3) Rowe [24] proposed a correlation to predict bubble size in a gas-solid fluidized bed (when size is
not
restricted by the column dimension) as:
(U 0 −U mf ) 12 ( H + H 0 ) 3 4
Db ( H ) = 1
…………….. (17)
g 4
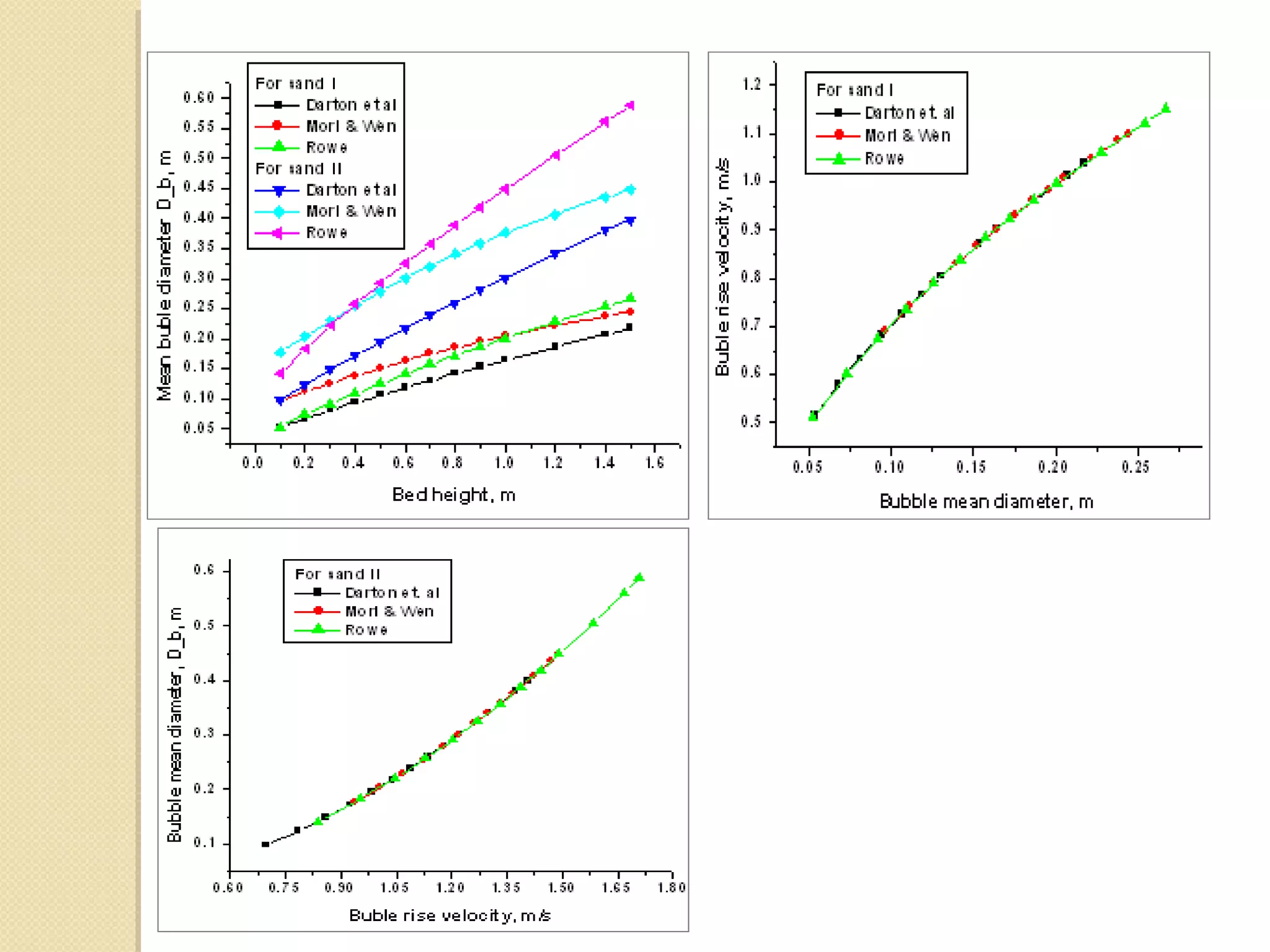
Table . Comparisons between bubble size for both sand materials:
Ref. Darton [23] Mori [22] Rowe [24]
Sand I Sand II Sand I Sand II Sand I Sand II
Uo 0.158 0.718 - - 0.158 0.718
Umf 0.045 0.205 0.045 0.205 0.045 0.205
H 0.1-1.5 0.1-1.5 0.1-1.5 0.1-1.5 0.1-1.5 0.1-1.5
Dbed 0.5 0.5 0.5 0.5 0.5 0.5
Abed 0.196 0.196 0.196 0.196 0.196 0.196
Nor 85 85 85 85 85 85
Dmax. 0.357 0.654 0.357 0.654 0.357 0.654
Dmin. 0.080 0.147 0.080 0.147 0.080 0.147
Db 0.053-0.217 0.098-0.399 0.096-0.244 0.176-0.448 0.052-0.267 0.142-0.588
Ub 0.514-1.038 0.697-1.406 0.691-1.101 0.936-1.491 0.509-1.151 0.838-1.708

17. Results & Conclusion
 The experimental and theoretical maximum pressure drop across the bed at 100, 125, 150 mm fixed bed
height conditions is 103, 139, 168 mm WC and 98.793, 136.85, 164.18 mm WC respectively for sand I and
44, 53, 65 mm WC and 40.098, 50.197, 66.642 mm WC respectively for sand II. The calculated u mf for
0.233 mm mean diameter sand I is 0.045 m/s and for 0.518 mm mean diameter sand II is 0.205 m/s. The
experimental value of umf varies from 0.05 to 0.06 m/s for sand I and for sand II, it varies from 0.206 to
0.209 m/s.
 During the experiment, it was observed that the experimental value of U t varies from 1.8 to 2.0 m/s for
sand I and from 4.3 to 4.6 m/s for sand II. It is then compared with the theoretical value i.e.1.9 m/s and
4.218 m/s. Therefore, the ratio Ut/Umf for sand I is 30 - 33.3 and for sand II is 20.87 – 22.01 which shows
the workability range of the present bubbling bed cold model.
 Also it is observed that the bubble size varies from 0.080 m to 0.357 m for sand I, from 0.147m to 0.654 m
for sand II at three bed heights i.e. 0.1m, 0.125m and 0.150m. It is observed from the graph that mean
bubble size increases with increase in bed material height for both sand sizes. Also it is seen from the
graphs that the mean bubble size for both sand sizes varies almost linearly with bubble rise velocity i.e. it
increases when bubble rise velocity increase and vice versa. The bubble rise velocity varies from 0.514 to
1.708 m/s with superficial air velocity varies from 0.518m/s to 0.718m/s for both sand types.
 The hydrodynamics parameters like minimum fluidization velocity, minimum bubbling velocity, particle
terminal velocity and the bubble size at different bed heights have been studied. The present study on cold
model of bubbling fluidized bed with bubble caps distributor provides sufficient information on
hydrodynamic parameters like minimum fluidization velocity, terminal velocity, the bubble size and bubble
behavior in large beds, These parameters of a freely bubbling beds are needed to understand the contacting
of gas and solids mixing.

18. Future Work
Results will be used in hot model
bubbling fluidized bed gasifier for
generation of hydrogen from the biomass
gasification of rice husk.
A CFD analysis will be done.