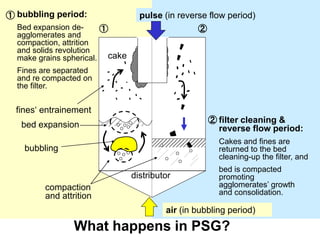
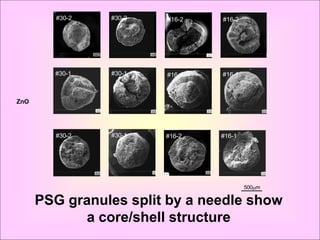
The document discusses binderless granulation and its potential, focusing on fundamental issues presented at the 7th International Symposium on Agglomeration. It details various experiments and findings related to pressure swing granulation, particle size distribution, and the effects of fluidizing gas velocity on agglomerate properties. The research indicates significant factors impacting granule density and suggests potential applications in the hard metal industry for improved material strength.

1. 7th Intl. Symp. on Agglomeration
Tuesday 29, May 2001
Binderless granulation –
Binderless granulation –
Its potential and relevant
Its potential and relevant
fundamental issues
fundamental issues
Masayuki Horio
Tokyo University of A&T
Koganei, Tokyo

2. Koganei ?
25 min from
Shinjuku
Nice place to escape

3. ①Fluidizing
Bag filter interval
15s
1s
②Compaction
interval
0 time[s] 7200
0.41m
f0.108m
Air ①Fluidizing ②Compaction
interval interval
(a) Test apparatus (b)Operation scheme
Pressure Swing Granulation
Nishii et al., U.S. Patent No. 5124100 (1992)
Nishii, Itoh, Kawakami,Horio, Powd. Tech., 74, 1 (1993)

4. Typical examples of PSG granules

5. Cumulative weight [%]
PSG
granules slide
from ZnO gate
dp=0.57m
after
1st fall
2nd fall
3rd fall
Particle size [10-6m]
PSG granules: weak but strong enough!
Change in PSD of PSG granules in realistic conditions

7. ① bubbling period: pulse (in reverse flow period)
Bed expansion de- ① ②
agglomerates and
compaction, attrition
and solids revolution
make grains spherical. cake
Fines are separated
and re compacted on
the filter.
fines‘ entrainement
② filter cleaning &
bed expansion reverse flow period:
Cakes and fines are
bubbling returned to the bed
cleaning-up the filter, and
bed is compacted
distributor promoting
compaction agglomerates’ growth
and attrition and consolidation.
air (in bubbling period)
What happens in PSG?

8. #30-2 #30-2 #16-2 #16-2
#30-1 #30-1 #16-1 #16-1
ZnO
#30-2 #30-1 #16-2 #16-1
500m
PSG granules split by a needle show
a core/shell structure

9. Fig.5

10. 1000
Median diameter [m10-6]
500
E
150
0.1 0.5 1.0
Superficial gas velocity [m/s]
Effect of fluidizing gas velocity on da

11. 1.2
Bulk density of granules [kg/m3]
w=0.4kg
1.0 0.2kg
with
gas velocity
0.8 and
solids charge
0.6
0 2.0 4.0 6.0
Maximum pressure difference for compaction [Pa104]
Factors affecting PSG granule density

12. Possibility of size control by surface
modification
Polar-polar interaction
between adsorbate molecules

13. 500
Median diameter [10-6m] Median diameter [10- 600
Median diameter [10-
adsorption at: 293K, 293K,
p(adsorbate): 4kPa 4kPa
400 500
No effect: desorbed
during PSG
6m]
6m]
300 400
0 3 6 9 12 0 3 6 9 12 Notes: At 573K all
Absorption time [h] Absorption time [h] hydroxyl groups
Median diameter [10-6m]
500 on TiO2 are
500 eliminated
573K, 573K, (Morimoto, et al.,
13.3kPa 13.3kPa Bull. Chem. Soc.
400 JPN, 21, 41(1988).
400 Highest heat of
immersion at 573K
300 (Wade &
No effect ?? Hackerman, Adv.
Chem. Ser., 43, 222,
200 300 (1964))
0 3 6 9 12 0 3 6 9 12
Absorption time Absorption time [h]
[h] heat treatment:at p<13.3Pa
(a) C2H5OH (b) NH4OH 523K, for 6 hrs
adsorption:
bed= f150x10mm
Mean size of PSG granules from TiO2 (0.27x10 m) -6 in a 0.03m3 vacuum
dryer
after heat treatment and surface modification PSG: charge=0.0333 kg
u0=0.55 m/s RH: 40-
50%
Nishii & Horio (Fluidization VIII, 1996) fluidiz.:15 s comp.: 1 s
total cycles=450

14. feed compositions
powd. dp(WC) WC Co wax*
x10-6m %wt %wt %wt
1 1.5 93.0 7.0 0.5
2 6.0 85.0 15.0 0.5
Powder 1 Powder 2 Powder 3 3 9.0 77.0 23.0 0.5
dp(cobalt)=1.3-1.5x10-6m
*) Tmp(wax)=330K
preparation:
1. grinding 2.5hr
2. vacuum drying
PSG:
Agglomerate 1 Agglomerate 2 Agglomerate 3 Dt=44mm
charge=150g
u0=0.548 m/s
P(TANK)=0.157 MPa
Hard Metal Application total cylces=64
SEM images of feeds and product granules

15. Transverse rupture strength [N/mm2]
PSG
method
convent-
ional
method
Co content [wt%]
Application to hard metal industry
Improved strength of sintered bodies

16. 500m 500m 500m 500m 500m
L : E=0 : 1 L : E=3 : 7 L : E=1 : 1 L : E=7 : 3 L : E=1 : 0
10m 10m 10m 10m 10m
L : E=0 : 1 L : E=3 : 7 L : E=1 : 1 L : E=7 : 3 L : E=1 : 0
top: PSG granules; second line: surface of agglomerate
(SEM)
Co-agglomeration of lactose and
ethensamide

17. 1,000 0.1
500
Chaouki et al.
300
Iwadate-Horio 0.05
da [m] Bubble size
Da [m]
200 0.03
(IHM)
100 0.02
50 bubbling
Morooka et al. 0.01 fixed bed
30 bed
20 u0=umf
u0=0.5m/s
2,000
0.005
10 0.01 0.03 0.1 0.3 1 3
0.01 0.03 0.1 0.3 1 3 10 30 100 1,000
dp [m] 500
IHM
(a) Effect of primary particle size 200
da [m]
100
5,000 50
Chaouki et al.
2,000 Morooka et al.
20
1,000 IHM
da [m]
10
500 0.01 0.03 0.1 0.3 1 3
200 u [m/s]
0
100
50 Chaouki et al. (c) Effect of u0
20 Morooka et al.
u0=0.5m/s
10
0.3 0.5 1 2 3 5
Ha [J]
(b) Effect of Hamaker const.
Comparison of model performances

18. 1.4E-3
1.2E-3
Lactose
1E-3 ZnO
da,calc [m] L:E=7:3
8E-4 L:E=1:1
L:E=3:7
6E-4
4E-4
2E-4
0E+0
0E+0 4E-4 8E-4 1.2E-3
2E-4 6E-4 1E-3 1.4E-3
da,obs[m]
Comparison of model predictions with observed data
Model (IHM) works !

19. Agglomerate: Fcoh>Frep, max
Collision: Fcoh<Frep, max
*
Non-cohesive Ha=0.4x10-19J Ha=1.0x10-19J Ha=2.0x10-19J
Kuwagi-Horio(2001)
Numerically determined agglomerates

20. Particle pressure around a Davidson’s
bubble

21. dp=100m, p=3700kg/m3
u0=0.1m/s, Ha=1.0×10-19J
0.411s 0.430s 0.450s 0.469s 0.489s
High particle normal stress right below
a bubble (Kuwagi-Horio(2001))

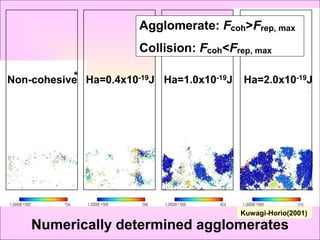
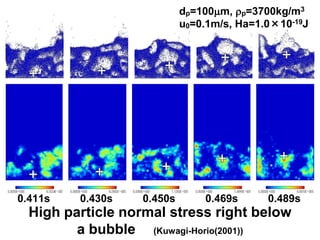
22. Comparison of previous model concepts
Authors Model External force/energy Cohesion force/energy Comments
FGa Fpp
Chaouki
[ ]
FGa = Fpp No bubble
FGa =  d a3
hwd p
hw
et al. Fpp =
2 1+ 8 2 3 hydrodynamic
 ag
6 16 
effects included.
Force balance Hr
van der Waals force
gravity force ≒drag force
between primary particles
No bubble
v=u mf Etotal =(Ekin+Elam ) Esplit
hydrodynamic
Etotal=(Ekin+Elam ) h w (1- a)d a2
Morooka Elaminer =3u mfd a2 Esplit =
effects included.
=Esplit shear
322 If 3 umf <hw (1-a)
et al. Ekinetic =mu mf 2/2 Etotal  ad p /(32d p  a),
Energy balance energy required to negative d a is
laminar shear + kinetic force
break an agglomerate obtained.
expansion Fcoh,rup
Fexp = Fcoh,rup exp = - Ps Bed expansion
force caused by
 Db ag(-Ps)d a2 Had a(1- a)
bubble Fexp = Fcoh,rup = bubbles is
Iwadate-Horio 2n k 242 equated with
Force balance cohesive rupture
force.
bed expansion force cohesive rupture force

23. (a) example force balance and (b) Limiting size of agglomerates
two solutions
The critical condition
stable point unstable point
1E-4
1E-4
1E-5
^
Dbag(-Ps)d a2 B 1E-5
Fexp= 2nk
1E-6
A easy to 1E-6
C
log F[N]
log F[N]
1E-7
defluidize 1E-7
fluidized
1E-8 1E-8
saddle point
Hada(1- a)
Fcoh,rup=
1E-9 1E-9
24 2
1E-10
1E-10
1E-6 3E-6 1E-5 3E-5 1E-4 3E-4 1E-3 3E-3
1E-6 3E-6 1E-5 3E-5 1E-4 3E-4 1E-3 3E-3
log d a[m] log da[m]
Force balance of I-H model
and the critical solution