Bab 10 membahas Hidrograf Satuan Sintetis Limantara, yaitu metode yang dikembangkan oleh Lily Montarcih Limantara pada 2006 untuk memperkirakan hidrograf banjir di sungai-sungai di Indonesia. Metode ini mempertimbangkan lima parameter fisik DAS yaitu luas, panjang sungai, jarak titik berat DAS ke outlet, kemiringan, dan koefisien kekasaran. Persamaan debit puncak, kurva naik, dan kurva turun men

1. BAB 10
HIDROGRAF SATUAN SINTETIS LIMANTARA
10.1. Pengertian Hidrograf Satuan Sintetis
1
Berdasarkan cara-cara untuk mendapatkan hidrograf satuan pengamatan,
diperlukan serangkaian data antara lain data tinggi muka air (rekaman AWLR),
data pengukuran debit, data hujan harian dan data hujan jam-jaman dari ARR.
Data tersebut seringkali sulit diperoleh atau bahkan tidak tersedia sama sekali.
Untuk membuat hidrograf banjir pada sungai-sungai yang tidak ada atau
sedikit sekali dilakukan pengamatan (observasi) hidrograf banjirnya, maka perlu
dicari karakteristik atau parameter daerah pengaliran tersebut terlebih dahulu.
Karakteristik atau parameter tersebut antara lain waktu untuk mencapai puncak
hidrograf, lebar dasar, luas, kemiringan, panjang alur terpanjang, koefisien
limpasan dan sebagainya. Untuk sungai-sungai yang tidak mempunyai hidrograf
banjir pengamatan, biasanya digunakan hidrograf-hidrograf sintetis yang telah
dikembangkan di negara-negara lain, yang parameter-parameternya harus
disesuaikan terlebih dahulu dengan karakteristik daerah pengaliran yang ditinjau.
Hidrograf Satuan Sintetis (HSS) yang telah dikembangkan oleh para pakar
antara lain HSS Snyder, HSS Nakayasu, HSS SCS, HSS Gama I, HSS
Limantara dan lain-lain. Hidrograf Satuan Sintetis ini dikembangkan berdasarkan
pemikiran bahwa pengalihragaman hujan menjadi aliran baik akibat pengaruh
translasi maupun tampungan, dipengaruhi oleh sistem daerah pengalirannya.
Hidrograf Satuan Sintetis merupakan suatu cara untuk memperkirakan

2. 2
penggunaan konsep hidrograf satuan dalam suatu perencanaan yang tidak
tersedia pengukuran-pengukuran langsung mengenai hidrograf banjir.
Bab ini memaparkan tentang Hidrograf Satuan Sintetis (HSS) Limantara,
yang asalnya dari Indonesia, ditemukan oleh Lily Montarcih Limantara,
tahun 2006. Lokasi penelitian di sebagian Indonesia dianggap mewakili: Jawa (6
DAS, 67 Sub DAS), Bali (2 DAS, 13 Sub DAS), Lombok (1 DAS, 5 Sub DAS) dan
Kalimantan Timur (1 DAS, 9 Sub DAS).
10.2. Parameter-parameter fisik DAS
Parameter DAS yang dipakai dalam Hidrograf Satuan Sintetis Limantara
ada 5 antara lain
1. Luas DAS (A)
2. Panjang sungai utama (L)
3. Panjang sungai diukur sampai titik terdekat dengan titik berat DAS (Lc)
4. Kemiringan sungai (S)
5. Koefisien kekasaran (n)
Masing-masing parameter tersebut di atas bisa diuraikan sebagai berikut:
1. Luas DAS (A)
Luas DAS (A) diperkirakan dengan mengukur daerah itu pada peta DAS. Jika
dihitung per-satuan luas, banjir yang terjadi di daerah dengan luas yang kecil
akan lebih besar dibandingkan banjir yang terjadi di sungai dengan DAS yang

3. 3
lebih luas.. Hal ini disebabkan karena di DAS yang kecil, air hujan mudah
mencapai sungai sedangkan pada DAS yang luas kemungkinan terdapat danau,
rawa, kolam, tanah yang porous (misalnya pasir) dan lain-lain, yang dapat
menahan air hujan. Luas DAS dipandang berpengaruh besar terhadap debit
puncak. DAS yang kecil memiliki tanggapan yang berbeda dengan DAS yang
besar, terutama tentang hubungannya dengan peristiwa limpasan.
2. Panjang sungai utama (L)
Panjang sungai (L) merupakan jarak dari outlet ke batas daerah aliran, yang
diukur sepanjang saluran aliran utama. Semakin panjang sungai, maka jarak
antara tempat jatuhnya hujan dengan outlet semakin besar, sehingga waktu
yang diperlukan air hujan untuk mencapai outlet lebih lama dan akan
menurunkan debit banjir. Hal ini disebabkan karena makin panjang sungai makin
banyak memberikan kesempatan bagi air hujan untuk mengalir sebagai
limpasan. Dengan demikian jumlah kehilangan air akan semakin besar.
3. Panjang sungai diukur sampai titik terdekat dengan titik berat DAS (Lc)
Lc merupakan panjang sungai dari outlet sampai titik berat DAS dan diukur
sepanjang aliran utama. Parameter ini didasarkan pada penelitian Gupta (1967),
antara lain dalam upayanya untuk mengaitkan besarnya debit puncak dengan
faktor-faktor fisik DAS. Untuk DAS yang cenderung menyempit di bagian hilir,
maka titik berat DAS akan terletak hampir ke hulu. Walaupun Lc cenderung
panjang, namun dengan kondisi DAS menyempit ke bagian hilir, maka akan
mempercepat naiknya debit puncak (waktu untuk mencapai debit puncak relatif

4. 4
singkat). Sebaliknya untuk DAS yang mempunyai lebar cenderung merata dari
hulu ke hilir, maka titik berat DAS akan terletak hampir di tengah DAS. Dalam hal
ini walaupun Lc relatif pendek, dengan kondisi DAS yang lebar, akan
memperlambat naiknya debit puncak (waktu untuk mencapai debit puncak relatif
lama).
4. Kemiringan sungai (S)
Kemiringan sungai (S) merupakan kemiringan sungai utama. Pada umumnya
hanya sungai utama yang diperhatikan dalam menggambarkan kemiringan DAS
secara umum. Kemiringan sungai secara rasional berpengaruh terhadap debit
puncak (Qp). Dengan kemiringan yang curam akan mempercepat waktu untuk
mencapai puncak banjir karena limpasan semakin cepat masuk ke sungai.
Kemiringan sungai utama menentukan kecepatan aliran dalam saluran, seperti
halnya liku resesi hidrograf yang digambarkan oleh pengosongan tampungan.
Kemiringan sungai yang curam akan mempercepat pengosongan tampungan
dan akan menghasilkan liku resesi hidrograf yang curam, sehingga menjadikan
waktu dasar hidrograf menjadi pendek. Dalam banyak kasus, kemiringan DAS
yang landai justru menghasilkan debit puncak yang lebih besar. Taylor dan
Cordery (1991) menyarankan cara menghitung kemiringan sungai dengan
anggapan aliran seragam. Dengan alasan kecepatan berbanding lurus dengan
akar kemiringan sungai (rumus Manning), maka prosedur perhitungan
kemiringan sungai adalah dengan membuat seimbang segmen-segmen sungai
dengan akar kemiringannya. Jadi, jika sungai dengan kekasaran Manning yang
sama dibagi dengan N segmen dengan kemiringan masing-masing Si (Gambar

5. 2), dengan kecepatan aliran adalah sama (V1 = V2 = V3 = VN), maka indeks
kemiringan sederhana menjadi:
S = (SÖSi/N)2 …….. Si » DE / DL
dengan
DE = beda elevasi dasar sungai (m)
DL = panjang segmen sungai (m)
5. Koefisien kekasaran (n)
Di dalam DAS terdapat hutan dan beberapa bagian tegalan, sawah, dan
pemukiman, yang membutuhkan perkiraan koefisien kekasaran (n). Koefisien
kekasaran (n) untuk lahan pertanian dengan tanaman diperkirakan sebesar
0,035 sedangkan untuk hutan atau semak belukar sebesar 0,07. Dengan
persamaan garis linier pada 2 titik yaitu pada kondisi tidak terdapat hutan dan
kondisi hutan seluruhnya, maka (Chow, 1988):
n = 0,035 (1 + Af/A)
dengan
5

6. n = koefisien kekasaran DAS
Af = luas hutan
A = luas DAS
Berdasarkan rumus di atas, jika luas hutan 100% (DAS seluruhnya berupa
hutan), maka akan diperoleh koefisien kekasaran DAS: n = 0,070. Sebaliknya
jika tidak ada hutan sama sekali (dalam arti Af = 0), maka akan diperoleh
koefisien kekasaran DAS: n = 0,035. Seperti diketahui, hutan pada umumnya
ditumbuhi tanaman-tanaman (pohon-pohon) yang besar sehingga
menggambarkan kekasaran DAS cukup besar, dalam arti akan menghambat
jalannya air hujan yang melimpas. Sedangkan untuk sawah dan tegalan hanya
ditumbuhi tanaman yang relatif kecil dan dianggap tidak cukup kuat dalam
menghambat air hujan yang melimpas. Demikian juga daerah pemukiman,
dianggap tidak cukup kasar untuk menghambat jalannya air hujan yang
melimpas. Berdasarkan alasan tersebut, Chow (1988) hanya memasukkan faktor
luas hutan dalam perhitungan koefisien kekasaran DAS.
10.3. Persamaan HSS Limantara
A. Persamaan Debit Puncak
Qp = 0,042.A0,451.L0,497.Lc0,356.S-0,131.n0,168
dengan
Qp = debit puncak banjir hidrograf satuan (m3/dt/mm)
A = luas DAS (km2)
L = panjang sungai utama (km)
6

7. Lc = panjang sungai dari outlet sampai titik terdekat dengan titik berat
DAS (km)
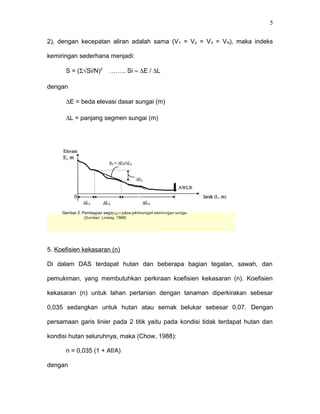
S = kemiringan sungai utama
n = koefisien kekasaran DAS
0,042 = koefisien untuk konversi satuan (m0,25/dt)
B. Persamaan Kurva Naik
Qn = Qp. [(t/Tp)]1,107
dengan
Qn = debit pada persamaan kurva naik (m3/dt/mm)
Qp = debit puncak hidrograf satuan (m3/dt/mm)
t = waktu hidrograf (jam)
Tp = waktu naik hidrograf atau waktu mencapai puncak hidrograf (jam)
C. Persamaan kurva turun:
Qt = Qp.100,175(Tp – t)
dengan
7
Qt = debit pada persamaan kurva turun (m3/dt/mm)
Qp = debit puncak hidrograf satuan (m3/dt/mm)
Tp = waktu naik hidrograf atau waktu mencapai puncak hidrograf (jam)
t = waktu hidrograf (jam)
0,175 = koefisien untuk konversi satuan (dt-1)

8. 10.4. Analisa Dimensi
A. Persamaan Debit Puncak Banjir (Qp)
Qp = 0,042.A0,451.L0,497.Lc0,356.S-0,131.n0,168
analisa dimensinya sbb:
[ L ]2 [ T ]-1 = [ L ]0,25 [ T ]-1 [ L 2 ]0,451 [ L ]0,492 [ L ]0,356
[ L ]2 [ T ]-1 = [ L ]0,25 [ T ]-1 [ L ]0,902 [ L ]0,492 [ L ]0,356
[ L ]2 [ T ]-1 = [ L ]0,25 + 0,902 + 492 +0,356 [ T ]-1
[ L ]2 [ T ]-1 = [ L ]2 [ T ]-1
B. Persamaan Kurva Naik (Qn)
Qn = Qp. [(t/Tp)]1,107
analisa dimensinya sbb:
[ L ]2 [ T ]-1 = [ L ]2 [ T ]-1 { [ T ]-1 / [ T ]-1 }1,107
[ L ]2 [ T ]-1 = [ L ]2 [ T ]-1 x 1
[ L ]2 [ T ]-1 = [ L ]2 [ T ]-1
C. Persamaan Kurva Turun (Qt)
Qt = Qp.e0,175(Tp – t)
analisa dimensinya sbb:
ln Qt = 0,175 (Tp – t) x ln Qp
ln [ L ]2 [ T ]-1 = [ T ]-1 [ T ]1 x ln [ L ]2 [ T ]-1
ln [ L ]2 [ T ]-1 = 1 x ln [ L ]2 [ T ]-1
[ L ]2 [ T ]-1 = [ L ]2 [ T ]-1
8

9. 10.5. Batasan keberlakuan HSS Limantara
HSS Limantara dapat diterapkan pada DAS lain yang memiliki kemiripan
karakteristik dengan DAS-DAS di lokasi penelitian. Spesifikasi teknik HSS
Limantara disajikan pada tabel berikut
Tabel Spesifikasi Teknik HSS Limantara
Uraian Notasi Satuan Kisaran
Luas DAS A km2 0,325 – 1667,500
Panjang sungai utama L km 1,16 – 62,48
Jarak titik berat DAS ke outlet Lc km 0,50 – 29,386
Kemiringan sungai utama S - 0,00040 – 0,14700
Koefisien kekasaran DAS N - 0,035 – 0,070
Bobot luas hutan Af % 0,00 - 100
10.6. Perkiraan Waktu Puncak Banjir (Tp)
Untuk memperkirakan waktu puncak banjir (Tp) bisa dipakai rumus seperti
pada Nakayasu sbb:
Tp = tg + 0,8 tr
dengan:
Tp = tenggang waktu (time lag) dari permulaan hujan sampai
puncak banjir  jam
tg = waktu konsentrasi hujan  jam
Cara menentukan tg:
Jika L ³ 15 km, maka tg = 0,40 + 0,058 L
L < 15 km, maka tg = 0,21 L0,7
dengan:
9

10. a = parameter hidrograf
tr = 0,5 x tg sampai 1 x tg
Contoh Soal
Parameter Sub DAS Garang (Jawa Tengah) berada dalam kisaran spesifikasi
teknik HSS Limantara, antara lain: A = 73,5 km2; L = 34,264 km; Lc = 22,16 km;
S = 0,0129 dan n = 0,0506. Akan dicari HSS nya dan Hidrograf Banjirnya
Penyelesaian:
L= 34,264 km
L ³ 15 km, maka tg = 0,40 + 0,058 L
tg = 0,40 + 0,058 x 34,264 = 2,387 jam
Tp = tg + 0,8 tr = 2,387 + 0,8 x 1 = 3,187 jam
Jadi:
- Qp = 0,042.A0,451.L0,497.Lc0,356.S-0,131.n0,168
= 0,042 x 73,50,451 x 34,2640,497 x 22,160,356 x 0,0129-0,131 x 0,05060,168
= 5,452
- Untuk t = 0 jam s/d 2 jam, memakai persamaan kurva naik
 Qn = Qp. [(t/Tp)]1,107
= 5,452 [(t/3,187)1,107
- Untuk t > 3,187 jam, memakai persamaan kurva turun
Qt = Qp.100,175(Tp – t)
= 5,452 x 100,175(3,187-t)
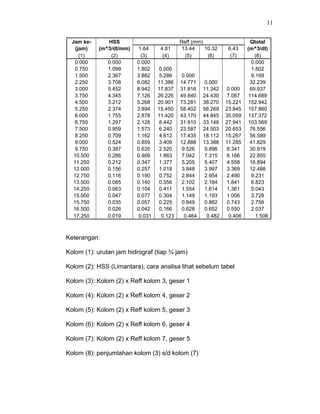
Analisa HSS (Limantara) dan Hidrograf Banjir ditabelkan sbb.:
10

11. Jam ke- HSS Reff (mm) Qtotal
(jam) (m^3/dt/mm) 1.64 4.81 13.44 10.32 6.43 (m^3/dt)
(1) (2) (3) (4) (5) (6) (7) (8)
0.000 0.000 0.000 0.000
0.750 1.099 1.802 0.000 1.802
1.500 2.367 3.882 5.286 0.000 9.169
2.250 3.708 6.082 11.386 14.771 0.000 32.239
3.000 5.452 8.942 17.837 31.816 11.342 0.000 69.937
3.750 4.345 7.126 26.226 49.840 24.430 7.067 114.689
4.500 3.212 5.268 20.901 73.281 38.270 15.221 152.942
5.250 2.374 3.894 15.450 58.402 56.269 23.845 157.860
6.000 1.755 2.878 11.420 43.170 44.845 35.059 137.372
6.750 1.297 2.128 8.442 31.910 33.148 27.941 103.569
7.500 0.959 1.573 6.240 23.587 24.503 20.653 76.556
8.250 0.709 1.162 4.612 17.435 18.112 15.267 56.589
9.000 0.524 0.859 3.409 12.888 13.388 11.285 41.829
9.750 0.387 0.635 2.520 9.526 9.896 8.341 30.919
10.500 0.286 0.469 1.863 7.042 7.315 6.166 22.855
11.250 0.212 0.347 1.377 5.205 5.407 4.558 16.894
12.000 0.156 0.257 1.018 3.848 3.997 3.369 12.488
12.750 0.116 0.190 0.752 2.844 2.954 2.490 9.231
13.500 0.085 0.140 0.556 2.102 2.184 1.841 6.823
14.250 0.063 0.104 0.411 1.554 1.614 1.361 5.043
15.000 0.047 0.077 0.304 1.149 1.193 1.006 3.728
15.750 0.035 0.057 0.225 0.849 0.882 0.743 2.756
16.500 0.026 0.042 0.166 0.628 0.652 0.550 2.037
17.250 0.019 0.031 0.123 0.464 0.482 0.406 1.506
Keterangan:
Kolom (1): urutan jam hidrograf (tiap ¾ jam)
Kolom (2): HSS (Limantara), cara analisa lihat sebelum tabel
Kolom (3): Kolom (2) x Reff kolom 3, geser 1
Kolom (4): Kolom (2) x Reff kolom 4, geser 2
Kolom (5): Kolom (2) x Reff kolom 5, geser 3
Kolom (6): Kolom (2) x Reff kolom 6, geser 4
Kolom (7): Kolom (2) x Reff kolom 7, geser 5
Kolom (8): penjumlahan kolom (3) s/d kolom (7)
11

12. 12

13. 13
Gambar Hidrograf Banjir DAS Garang
t (jam)
Q (m3/dt)

14. 14
t (jam)
Q (m3/dt)

15. 15

16. 16