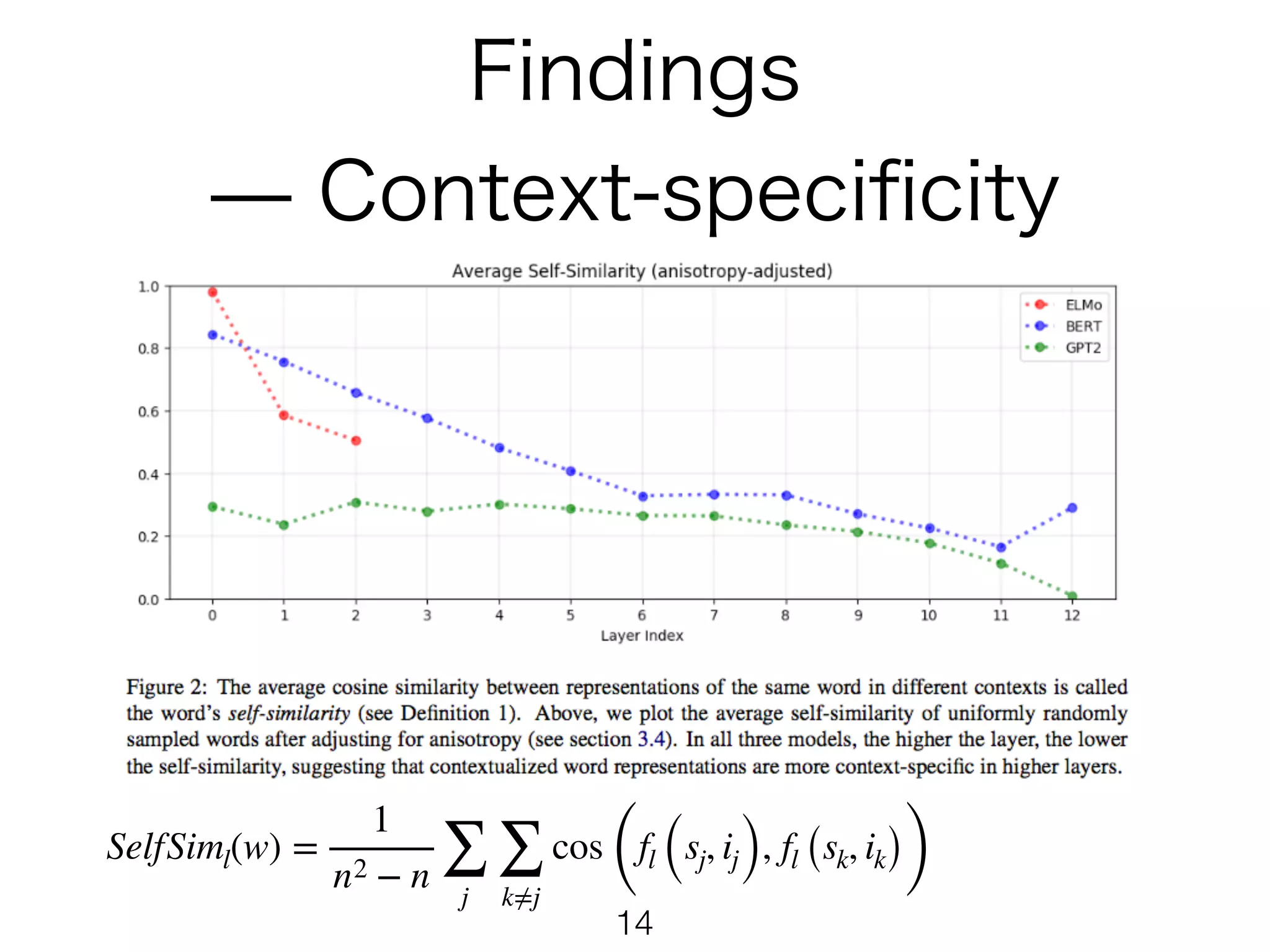
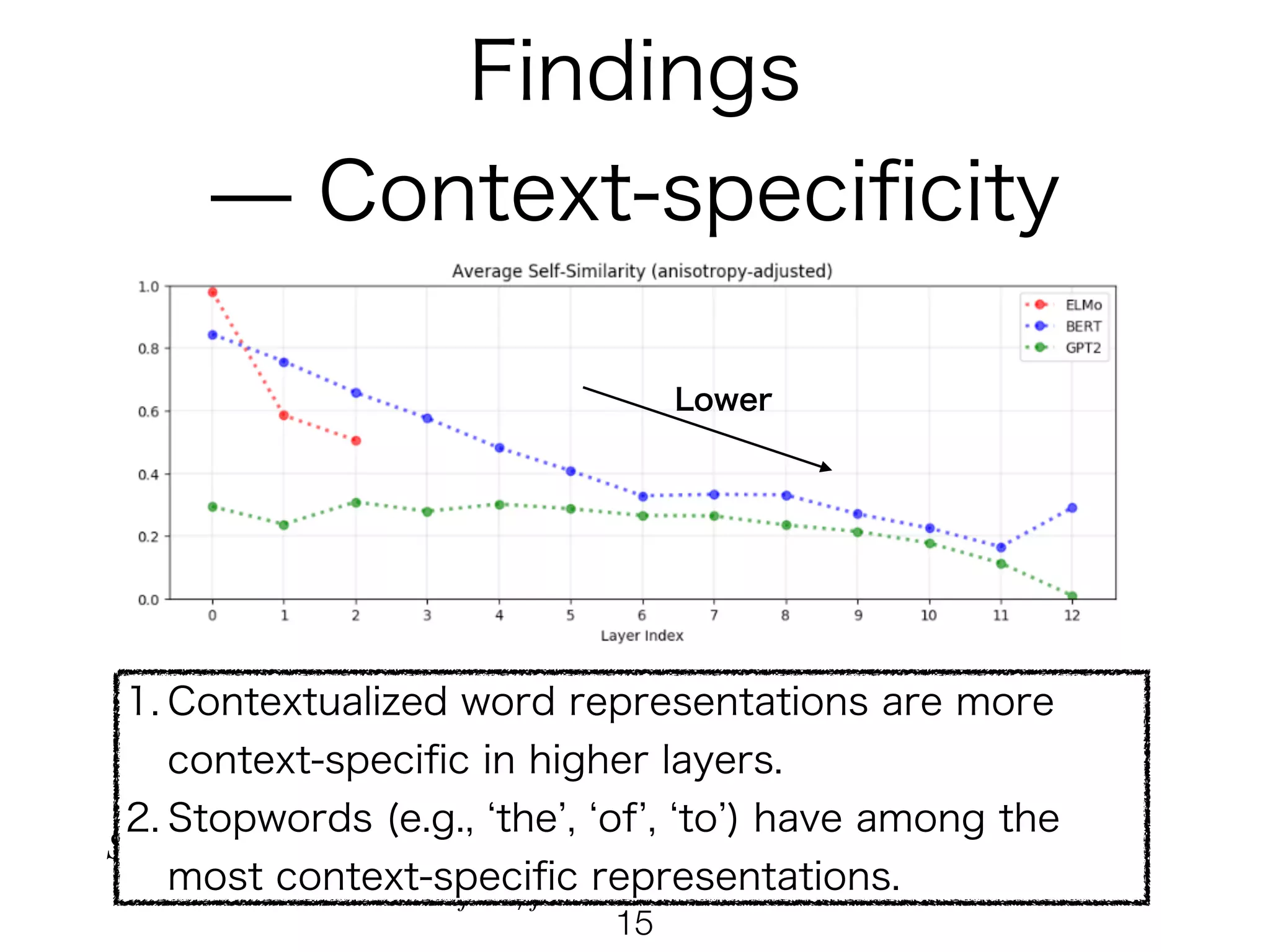
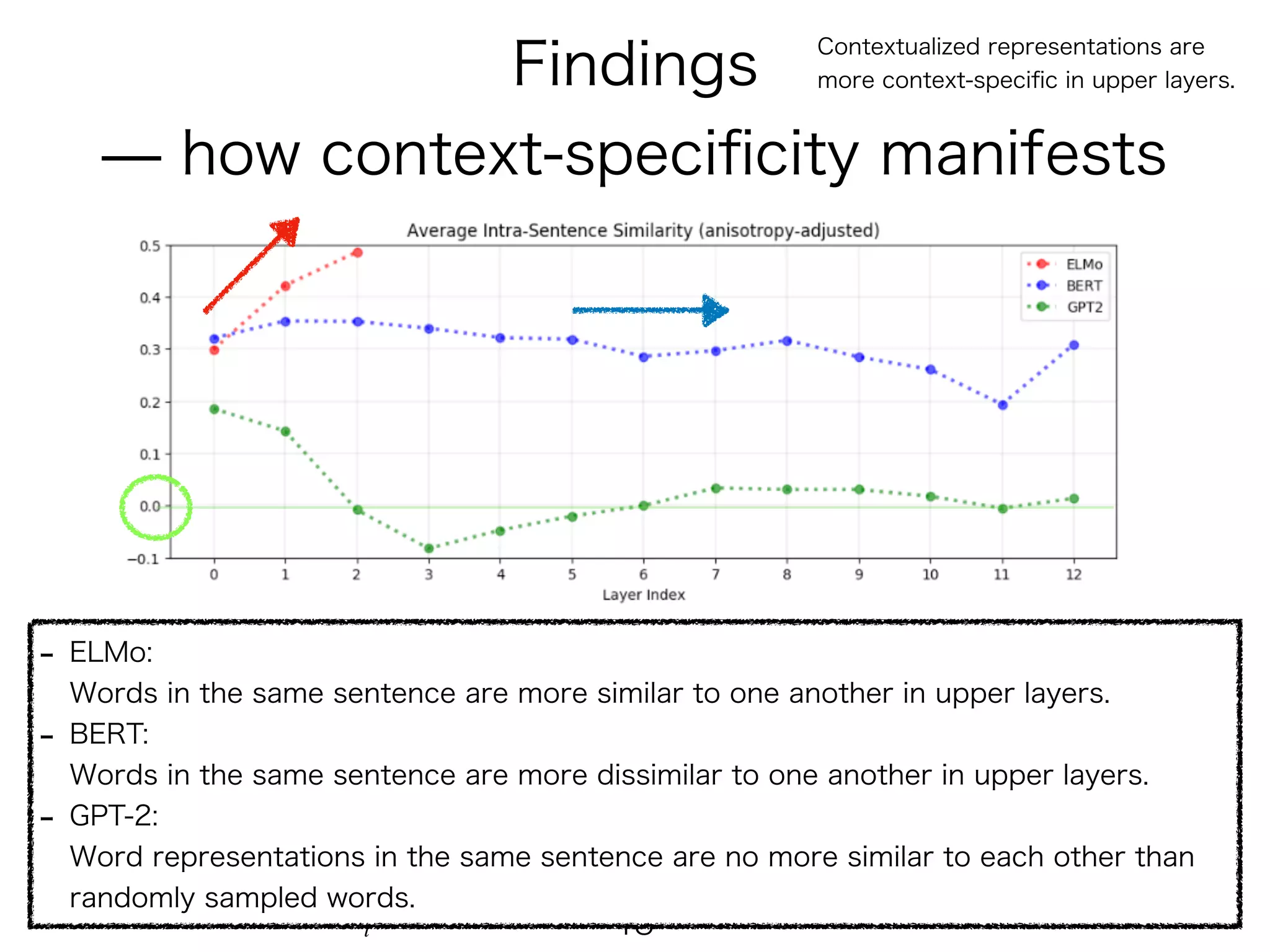
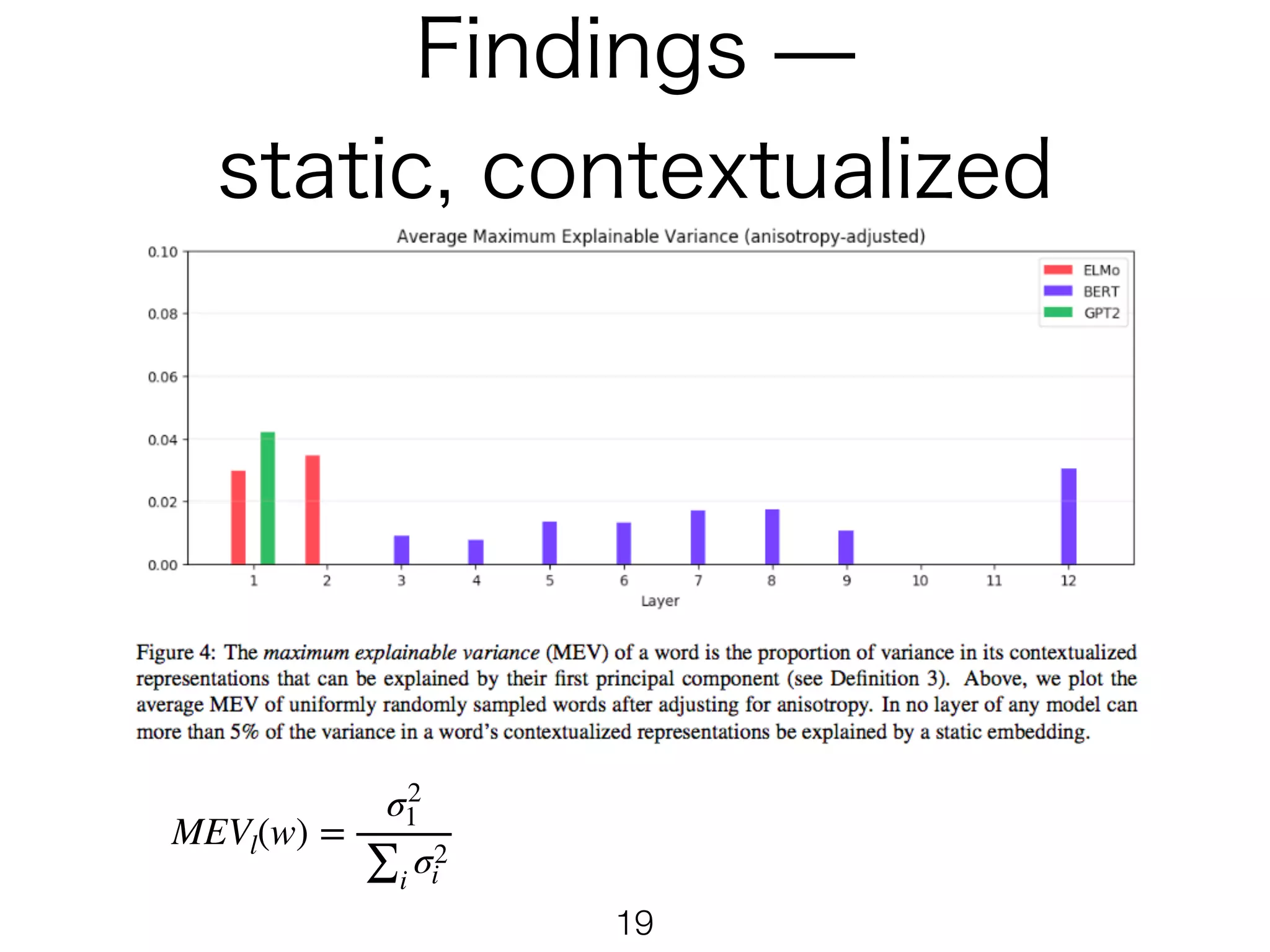
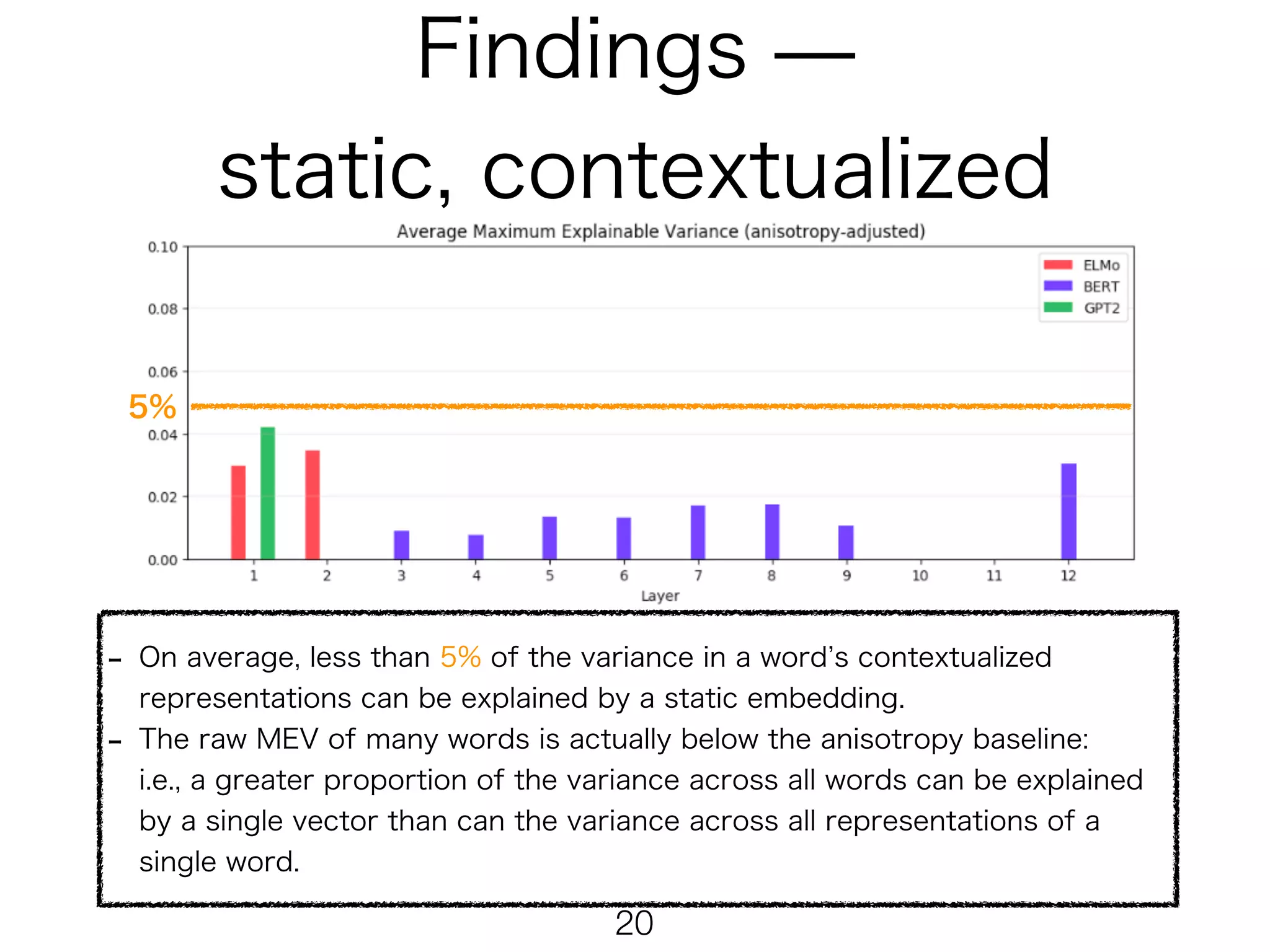
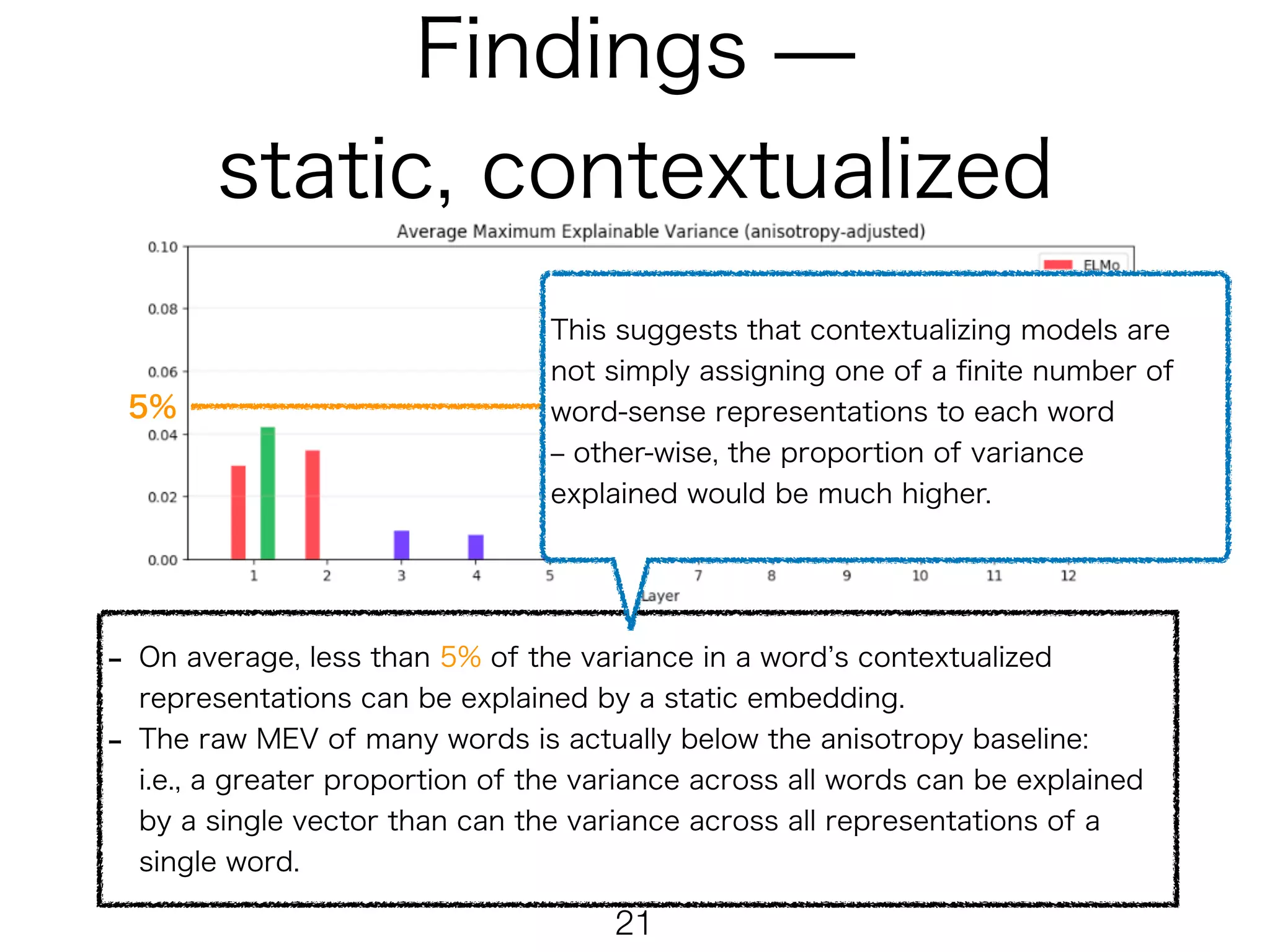
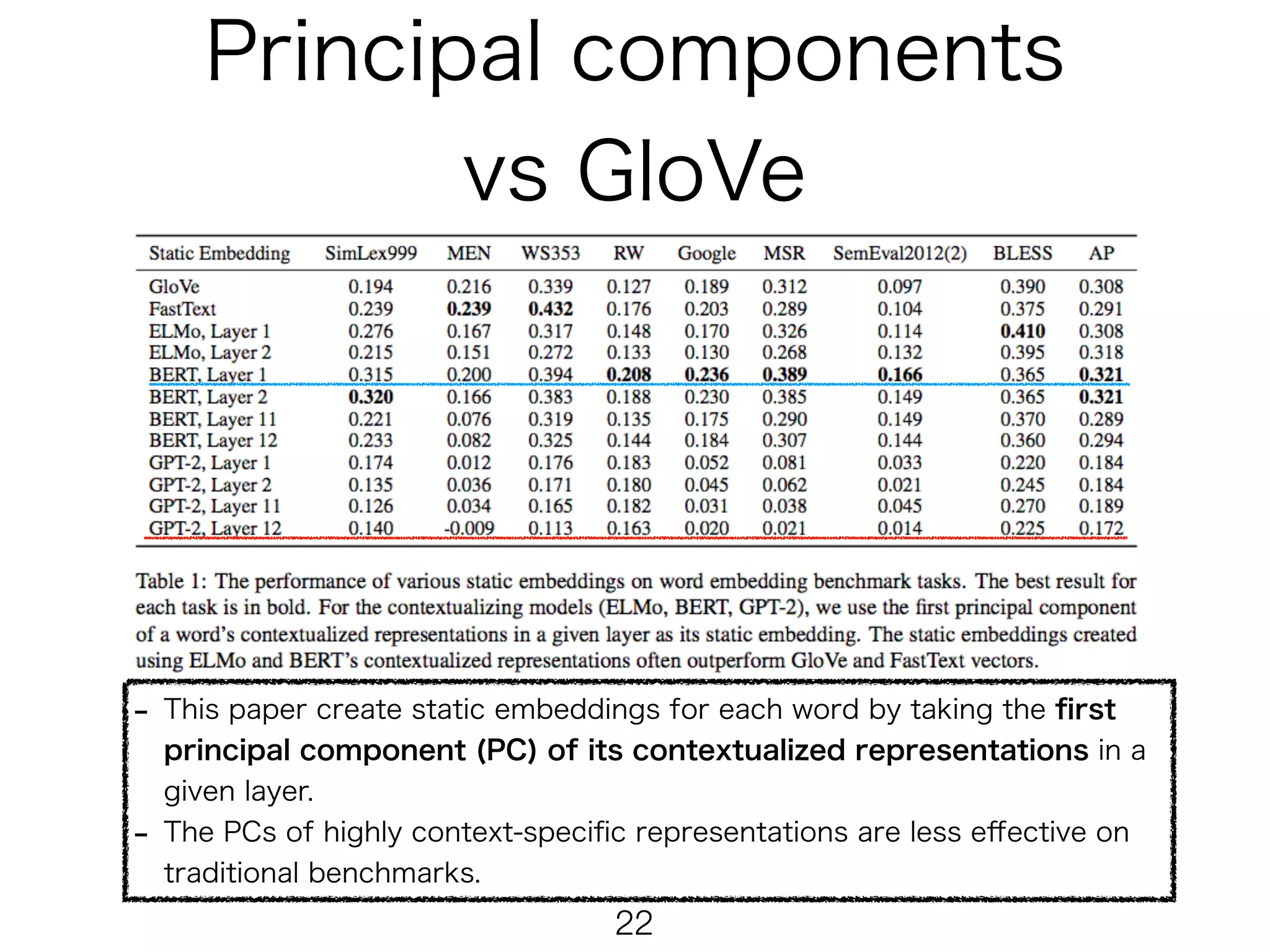
The document presents mathematical formulations for calculating self-similarity and intra-similarity measures using cosine similarity. It defines functions such as selfsiml and intrasiml, detailing their calculations based on input sequences and indices. Additionally, it introduces a baseline method for comparison of similarity metrics, highlighting differences between self-similarity and baseline values.



![!4
w {s1, . . . , sn}
{i1, . . . , in}
w = s1[i1] = . . . = sn[in]
fl(s, i) s[i]
l
SelfSiml(w) =
1
n2 − n ∑
j
∑
k≠j
cos
(
fl (sj, ij), fl (sk, ik))](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-4-2048.jpg)
![!5
s ⟨w1, . . . , wn⟩
fl(s, i) s[i]
l
IntraSiml(s) =
1
n ∑
i
cos ( ⃗sl, fl(s, i))
where ⃗sl =
1
n ∑
i
fl(s, i)](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-5-2048.jpg)
![!6
w {s1, . . . , sn}
{i1, . . . , in}
w = s1[i1] = . . . = sn[in]
fl(s, i) s[i] l
MEVl(w) =
σ2
1
∑i
σ2
i
[fl(s1, i1) . . . fl(sn, in)]
σ1 . . . σm](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-6-2048.jpg)
![!7
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]
𝒪
fl( ⋅ )
l](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-7-2048.jpg)
![!8
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]
𝒪
fl( ⋅ )
SelfSiml(w) = 0.95
Baseline(fl) = 0.00
Baseline(fl) = 0.99
Baseline(fl) = 0.00
Baseline(fl) = 0.99](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-8-2048.jpg)
![!9
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]
𝒪
fl( ⋅ )
SelfSiml(w) = 0.95
Baseline(fl) = 0.00
Baseline(fl) = 0.99
Baseline(fl) = 0.00
Baseline(fl) = 0.99](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-9-2048.jpg)
![!10
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]
𝒪
fl( ⋅ )
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]
SelfSim*l
(w) = SelfSiml(w) − Baseline (fl)](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-10-2048.jpg)
![!11
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-11-2048.jpg)
![!12
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-12-2048.jpg)
![!13
Baseline (fl) = 𝔼x,y∼U(𝒪) [cos (fl(x), fl(y))]](https://image.slidesharecdn.com/howcontextualized-191016123148/75/How-Contextual-are-Contextualized-Word-Representations-13-2048.jpg)