The document presents a seminar on high-dimensional data visualization by Fabian Keller, outlining various dimensionality reduction techniques such as PCA, LLE, Isomap, and t-SNE, as well as visualization methods including scatterplots and parallel coordinate plots. It emphasizes the necessity of choosing appropriate techniques based on application needs, citing several examples across different fields like biology, finance, and big data analysis. The conclusion highlights the importance of tailoring visualization methods to specific requirements in handling high-dimensional data.

1. High Dimensional Data Visualization
Presented by Fabian Keller
Seminar: Large Scale Visualization
Advisor: Steffen Koch
University of Stuttgart, Summer Term 2015

2. Motivation
What do you see?
16.07.2015 Fabian Keller 2

3. Motivation
I can see…
16.07.2015 Fabian Keller 3

4. Agenda
• Introduction
• Dimension Reduction Techniques
PCA / LLE / ISOMAP / t-SNE
• Visualization Techniques
Scatterplots / Parallel Coordinate Plots / Glyphs
• Conclusion
16.07.2015 Fabian Keller 4

5. Goal
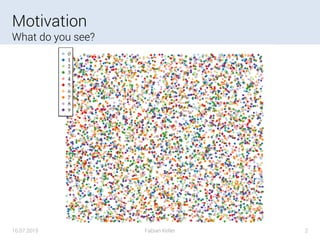
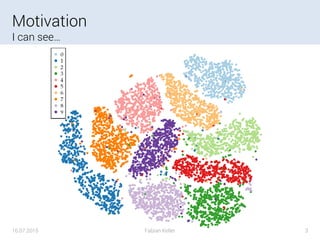
Of dimensionality reduction
• High Dimensional Data (>>1000 dimensions)
• Reduce Dimensions (for Clustering / Learning / …)
• Extract Meaning
• Visualize and Interact
16.07.2015 Fabian Keller 5
[c.f. Card et al 1999; dos Santos and Brodlie 2004]

6. Intrinsic Dimensionality
How many dimensions can we reduce?
2D  1D 3D  1D
16.07.2015 Fabian Keller 6
 Intrinsic Dimensionality: 1

7. Agenda
• Introduction
• Dimension Reduction Techniques
PCA / LLE / ISOMAP / t-SNE
• Visualization Techniques
Scatterplots / Parallel Coordinate Plots / Glyphs
• Conclusion
16.07.2015 Fabian Keller 7

8. Dimension Reduction
What techniques are there?
DR
Techniques
Linear
Principal
Component
Analysis
Non-Linear
Local
Local Linear
Embedding
Global
ISOMAP t-SNE
16.07.2015 Fabian Keller 8

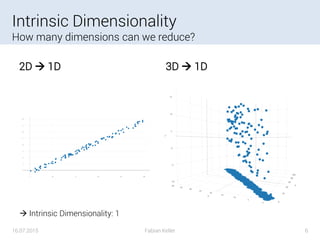
9. Principal Component Analysis (PCA)
Eigen-*
16.07.2015 Fabian Keller 9
• Linear, Global
• Find “Principal
Components”
• Minimize
Reconstruction Error
[isomorphismes, 2014]

10. Principal Component Analysis (PCA)
Eigen-Faces
16.07.2015 Fabian Keller 10

11. Local-Linear Embedding (LLE)
Assumes the data is locally linear
• Non-Linear, Local
• Select neighbors and
approximate linearly
• Map to lower
dimension
16.07.2015 Fabian Keller 11
[Roweis, 2000]

12. ISOMAP
Isometric feature mapping
16.07.2015 Fabian Keller 12
• Non-linear, Global
• K-Nearest Neighbors
• Construct
neighborhood graph
• Compute shortest
paths
[Balasubramanian, 2002]

13. t-SNE
Stochastic Neighbor Embedding
• Non-linear, Global
• Uses Gaussian
similarities
• Preserves the
similarities in lower
dimensions
16.07.2015 Fabian Keller 13

14. Agenda
• Introduction
• Dimension Reduction Techniques
PCA / LLE / ISOMAP / t-SNE
• Visualization Techniques
Scatterplots / Parallel Coordinate Plots / Glyphs
• Conclusion
16.07.2015 Fabian Keller 14

15. 2D Scatter Plots
Commonly used
• Easy Perception
• (No) Interaction
• Limited to two
dimensions
• Colors?!
16.07.2015 Fabian Keller 15

16. 2D Scatter Plot Matrices
Show relationships with scatter plots
• Slow perception
• May have interaction
• Does not scale well
16.07.2015 Fabian Keller 16

17. 2D Scatter Plot Matrices
Let an algorithm choose the plots
16.07.2015 Fabian Keller 17
[Zheng, 2014]

18. 3D Scatter Plots
Interactive
• Only one additional dimension
• Expensive interaction, useless without!
• Limited benefit compared to 2D scatter plots
16.07.2015 Fabian Keller 18
[Sedlmair, 2013]

19. Parallel Coordinate Plot
Display >2 dimensions
16.07.2015 Fabian Keller 19
Interaction Examples: https://syntagmatic.github.io/parallel-coordinates/
• Noisy
• Slow perception
• Meaning of x-axis?!
[Harvard Business Manager, 2015-07]

20. Glyphs
Encode important information
• Memorable semantics
• Small
• Details through
interaction
• Overwhelming?
16.07.2015 Fabian Keller 20
[Fuchs, 2013]

21. Glyphs
Domain-specific clues
16.07.2015 Fabian Keller 21
[Fuchs, 2014]

22. Glyphs
Time series data
16.07.2015 Fabian Keller 22
[Kintzel, 2011]

23. Conclusion
High Dimensional Data Visualization
• Lots of DR / visualization techniques
• Even more combinations
• Application needs to be tailored to needs
16.07.2015 Fabian Keller 23
“A problem well put is half-solved”
– John Dewey

24. Thank you for your attention!
Questions?

25. Literature
• Sedlmair, Michael; Munzner, Tamara; Tory, Melanie (2013): Empirical guidance on scatterplot and
dimension reduction technique choices.
• Zheng, Yunzhu; Suematsu, Haruka; Itoh, Takayuki; Fujimaki, Ryohei; Morinaga, Satoshi;
Kawahara, Yoshinobu (2014): Scatterplot layout for high-dimensional data visualization.
• Card, S. K., Mackinlay, J. D., and Shneiderman, B., editors. Readings in Information Visualization:
Using Vision to Think. Morgan Kaufmann, San Francisco. 1999.
• Fuchs, Johannes, et al. "Evaluation of alternative glyph designs for time series data in a small
multiple setting." Proceedings of the SIGCHI Conference on Human Factors in Computing
Systems. ACM, 2013.
• Christopher Kintzel, Johannes Fuchs, and Florian Mansmann. 2011. Monitoring large IP spaces
with ClockView.
• Fuchs, Johaness et al. “Leaf Glyph Visualizing Multi-Dimensional Data with Environmental Cues“.
2014.
• Balasubramanian, Mukund, and Eric L. Schwartz. "The isomap algorithm and topological
stability." Science 295.5552 (2002): 7-7.
• Roweis, Sam T.; Saul, Lawrence K. (2000): Nonlinear dimensionality reduction by locally linear
embedding.
• dos Santos, S. and Brodlie, K. Gaining understanding of multivariate and multidimensional data
through visualization. Computers & Graphics, 28(3):311–325. 2004.
• Harvard Business Manager, 2015-07: Andere Länder, anderer Stil
http://www.harvardbusinessmanager.de/heft/d-135395625.html
• isomorphismes (2014). pca - making sense of principal component analysis, eigenvectors &
eigenvalues - cross validated. http://stats.stackexchange.com/a/82427/80011
16.07.2015 Fabian Keller 25

26. Example Applications
• Biological / Medical (genes, fMRI)
• Finance (time series)
• Geological (climate, spatial, temporal)
• Big Data Analysis (Netflix Movie Rating Data)
16.07.2015 Fabian Keller 26

27. Other DR techniques
Matlab toolbox for dimensionality reduction
16.07.2015 Fabian Keller 27
• Principal Component Analysis
(PCA)
• Probabilistic PCA
• Factor Analysis (FA)
• Classical multidimensional
scaling (MDS)
• Sammon mapping
• Linear Discriminant Analysis
(LDA)
• Isomap
• Landmark Isomap
• Local Linear Embedding (LLE)
• Laplacian Eigenmaps
• Hessian LLE
• Local Tangent Space
Alignment (LTSA)
• Conformal Eigenmaps
(extension of LLE)
• Maximum Variance Unfolding
(extension of LLE)
• Landmark MVU
(LandmarkMVU)
• Fast Maximum Variance
Unfolding (FastMVU)
• Kernel PCA
• Generalized Discriminant
Analysis (GDA)
• Diffusion maps
• Neighborhood Preserving
Embedding (NPE)
• Locality Preserving Projection
(LPP)
• Linear Local Tangent Space
Alignment (LLTSA)
• Stochastic Proximity
Embedding (SPE)
• Deep autoencoders (using
denoising autoencoder
pretraining)
• Local Linear Coordination (LLC)
• Manifold charting
• Coordinated Factor Analysis
(CFA)
• Gaussian Process Latent
Variable Model (GPLVM)
• Stochastic Neighbor
Embedding (SNE)
• Symmetric SNE
• t-Distributed Stochastic
Neighbor Embedding (t-SNE)
• Neighborhood Components
Analysis (NCA)
• Maximally Collapsing Metric
Learning (MCML)
• Large-Margin Nearest Neighbor
(LMNN)
See: http://lvdmaaten.github.io/drtoolbox/