The document discusses the author's thesis that it is possible to generate provable verification conditions for full behavioral verification of object-based software in a modular fashion. Key points:
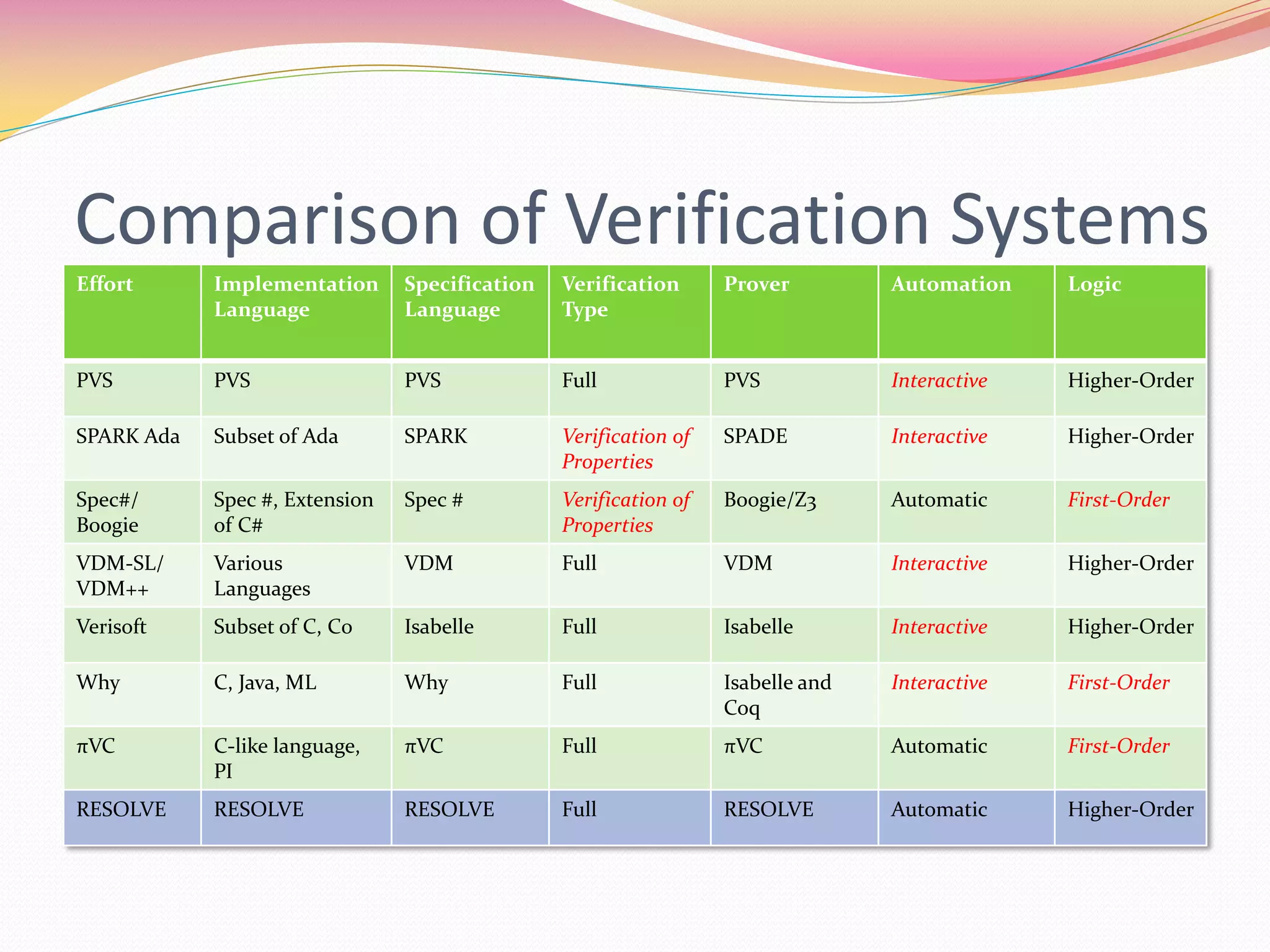
- The author uses the RESOLVE specification and implementation language for verification.
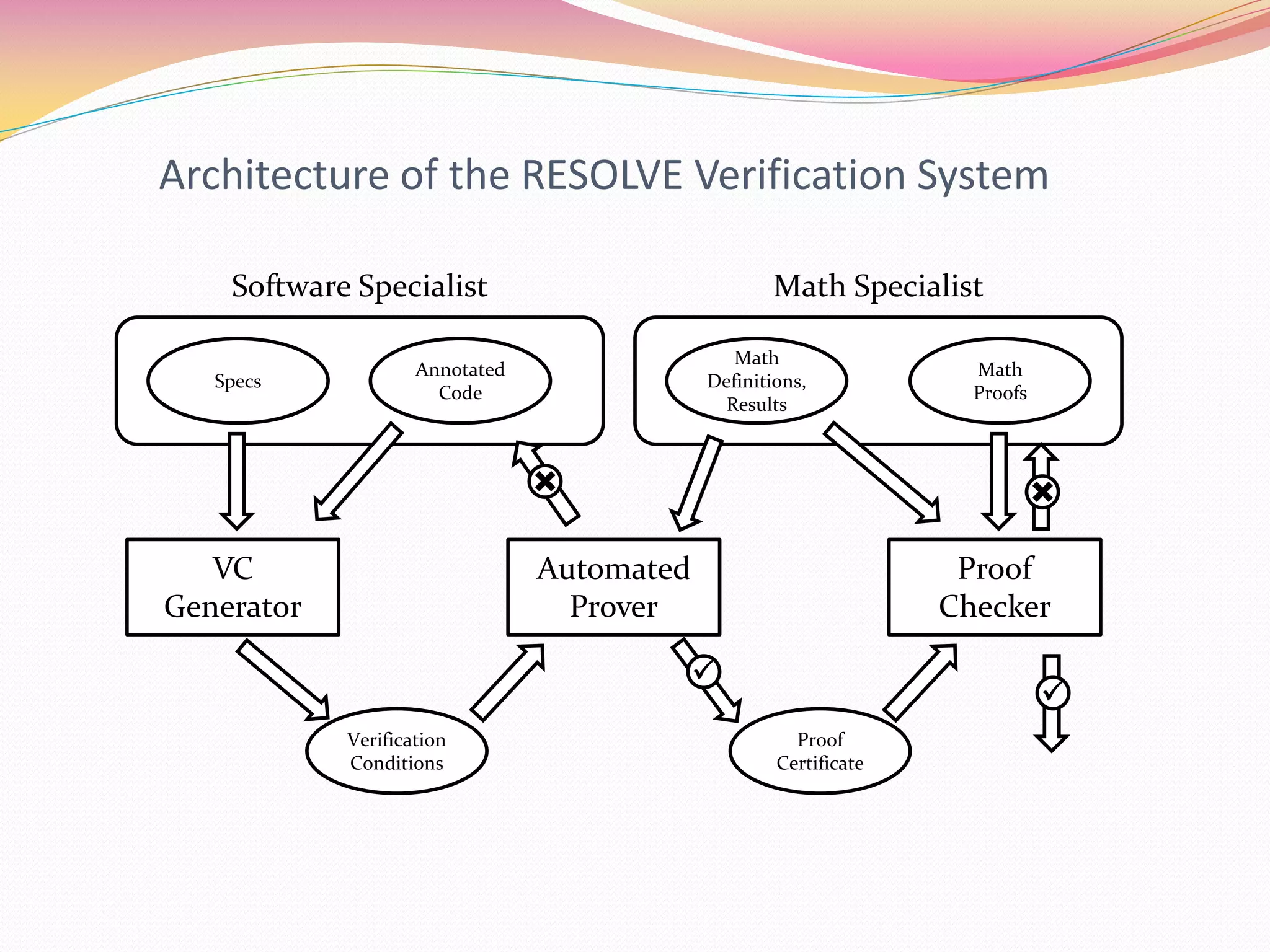
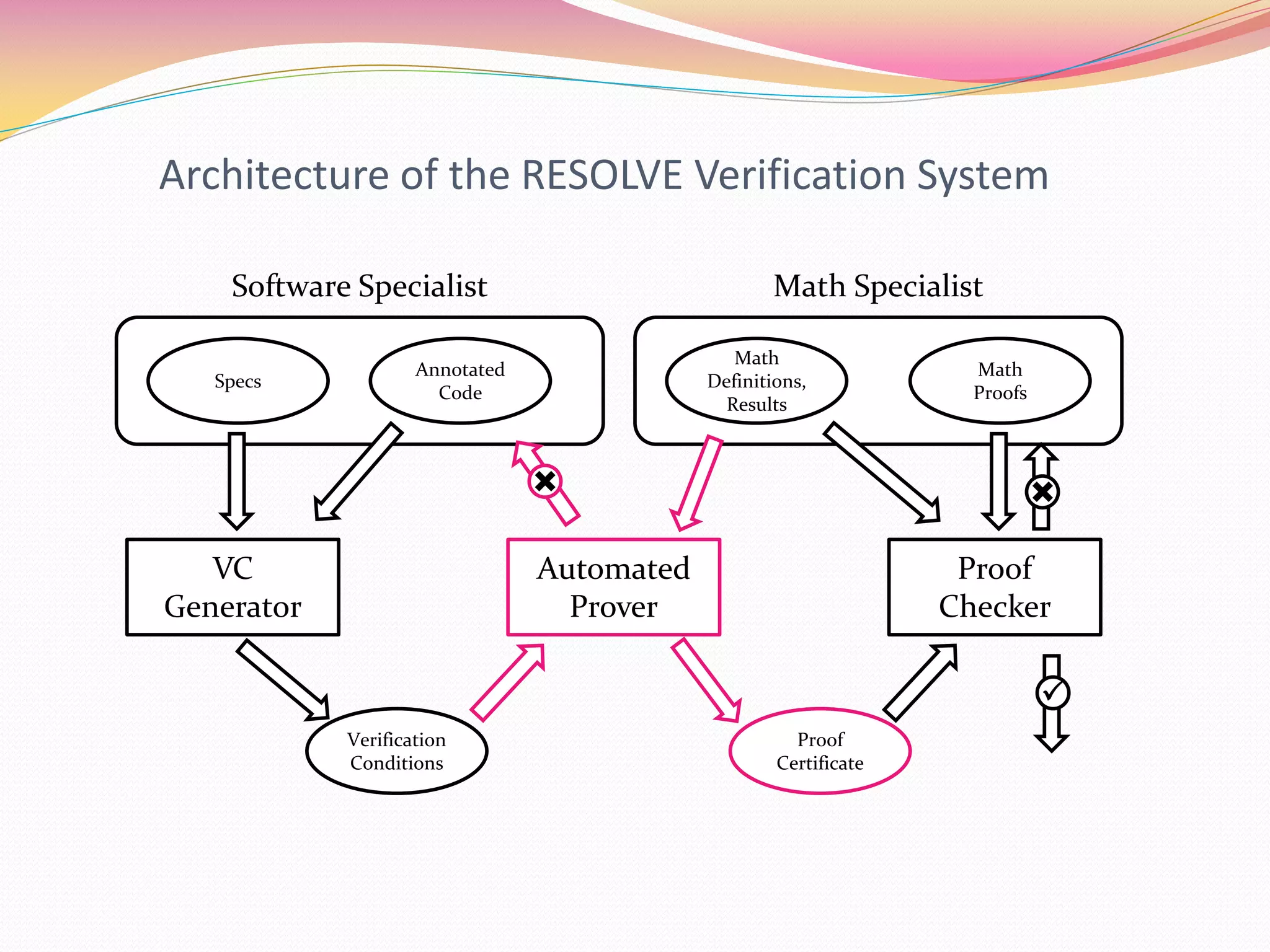
- The verification system architecture includes a VC generator, proof checker, automated prover, and annotated code.
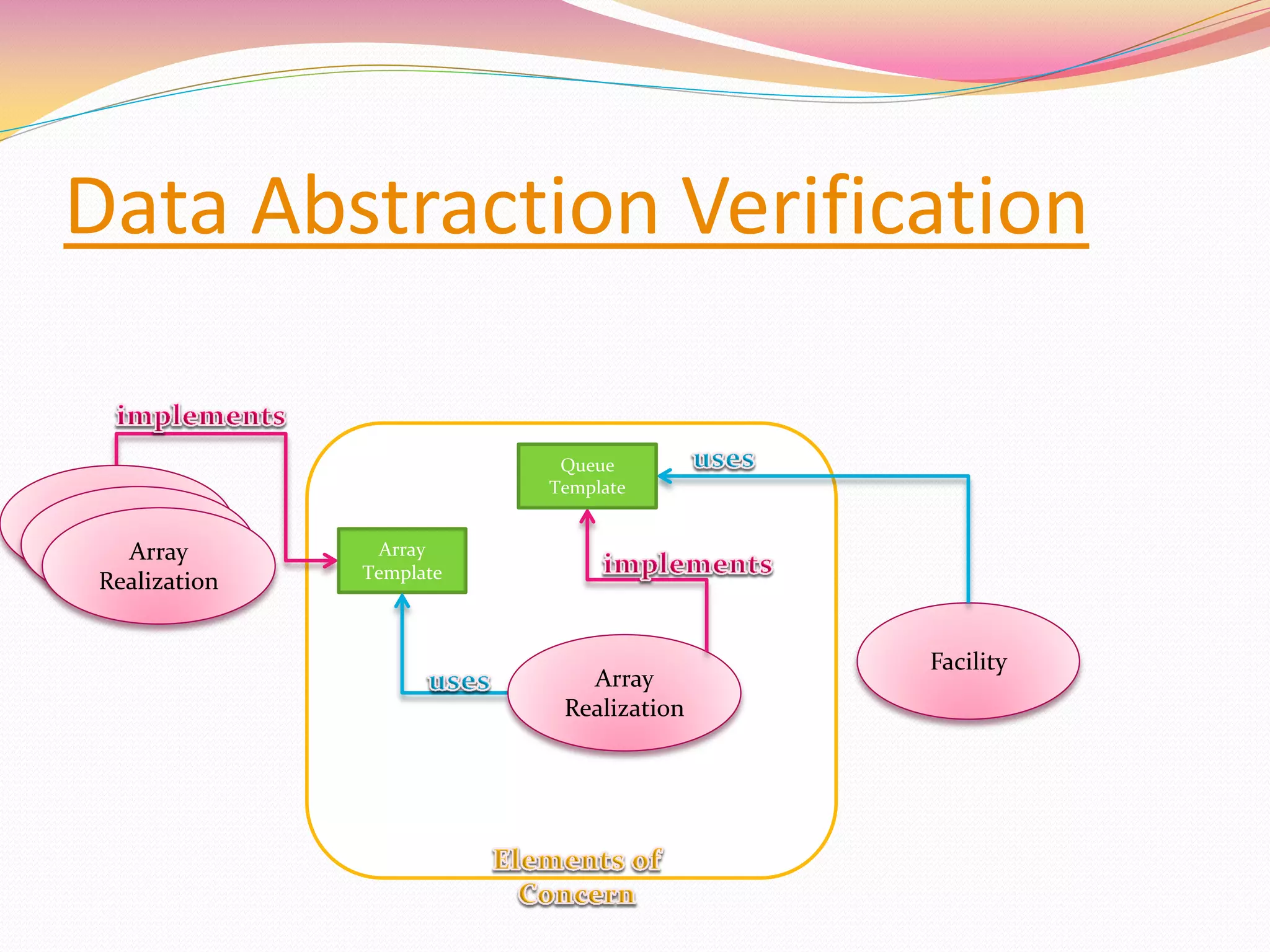
- The system aims to provide modular verification by verifying components one at a time using only specifications of reused components.
- The author has done research into mechanizing proof rules for constructs in modern languages to support automated verification.















































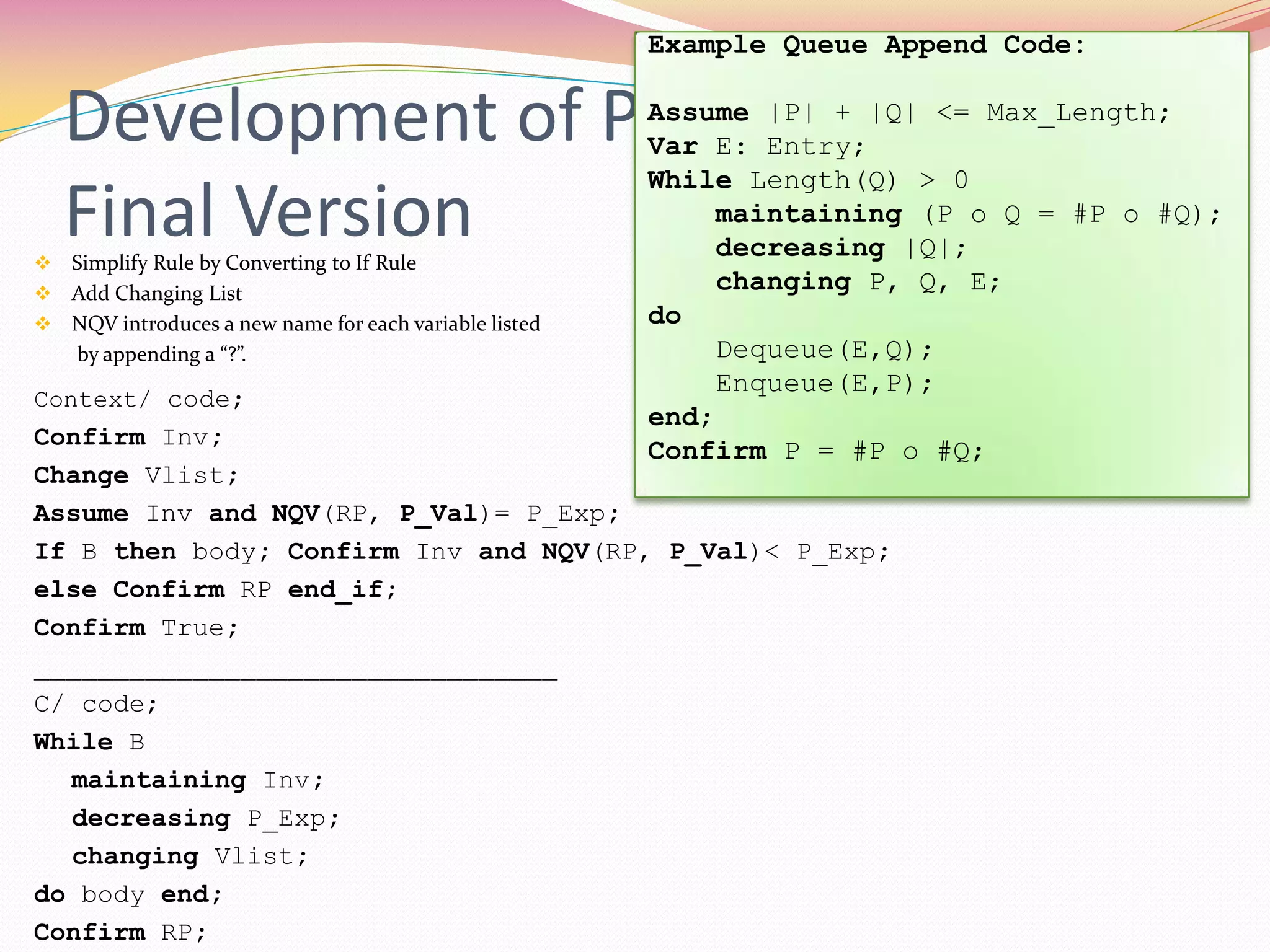




![Queue Append VC Generation
Part 1:
Assume ((Last_Char_Num > 0) and(((min_int <= 0) and(0 <
max_int)) and((Max_Length > 0) and(min_int <=
Max_Length) and (Max_Length <= max_int))));
Assume ((|Q| <= Max_Length) and((|P| <= Max_Length)
and((|P| + |Q|) <= Max_Length)));
Remember; Var E:Entry;
Confirm (P o Q) = (#P o #Q);
Change P:Modified_String_Theory.Str(Entry),
Q:Modified_String_Theory.Str(Entry), E:Entry, E:Entry;
Assume ((P o Q) = (#P o #Q) and P_val' = |Q|);
Confirm true;
Assume |Q| /= 0;
Dequeue(E, Q);
Enqueue(E, P);
Confirm ((P o Q) = (#P o #Q) and(|Q| < P_val'));
CDP = Operation P( updates t: T1; alters u: T2);
requires Pre/_t, u _;
ensures Post/_ #t, #u, t _;
Operation Call Rule:
C {CDP} code; Confirm Invk_Cond(P(a,b));
Assume Post[t⇝NQV(result, a), #t⇝a, #u⇝b];
Confirm result[a⇝NQV(result, a)];
____________________________________________
C {CDP} code; P( a, b); Confirm result/_ a, b _ ;](https://image.slidesharecdn.com/79e8963d-3ebe-40b5-8425-90f01390b6c3-160524003824/75/Harton-Presentation-56-2048.jpg)





![Change Rule Applied
Assume ((Last_Char_Num > 0) and(((min_int <= 0) and(0 <
max_int)) and((Max_Length > 0) and(min_int <=
Max_Length) and (Max_Length <= max_int))));
Assume ((|Q| <= Max_Length) and((|P| <= Max_Length)
and((|P| + |Q|) <= Max_Length)));
Remember;
Var E:Entry;
Confirm (P o Q) = (#P o #Q);
Confirm ((P' o Q'') = (#P o #Q) implies
(|Q''| /= 0 implies
(|Q''| /= 0 and (Q'' = (<E'> o Q') implies
((|P'| < Max_Length) and
(((P' o <E'>) o Q') = (#P o #Q) and
(|Q'| < |Q''|)))))))
Change Rule:
C code;
Confirm result[x⇝NQV(result, x)];
_____________________________________________
C code; Change x; Confirm result;](https://image.slidesharecdn.com/79e8963d-3ebe-40b5-8425-90f01390b6c3-160524003824/75/Harton-Presentation-62-2048.jpg)


![Remember Rule
Assume ((Last_Char_Num > 0) and(((min_int <= 0) and(0 <
max_int)) and((Max_Length > 0) and(min_int <=
Max_Length) and (Max_Length <= max_int))));
Assume ((|Q| <= Max_Length) and((|P| <= Max_Length)
and((|P| + |Q|) <= Max_Length)));
Confirm ((P o Q) = (P o Q) and
((P' o Q'') = (P o Q) implies
(|Q''| /= 0 implies
(|Q''| /= 0 and (Q'' = (<E'> o Q') implies
((|P'| < Max_Length) and
(((P' o <E'>) o Q') = (P o Q) and
(|Q'| < |Q''|))))))))
Remember Rule:
C code; Confirm result[#s⇝s, #t⇝t];
_____________________________________________
C code; Remember;
Confirm result/_ s, #s, t, #t, u, v, ⋯ _;](https://image.slidesharecdn.com/79e8963d-3ebe-40b5-8425-90f01390b6c3-160524003824/75/Harton-Presentation-65-2048.jpg)