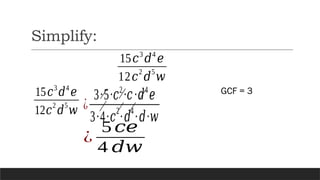
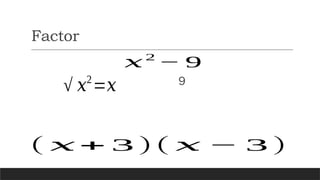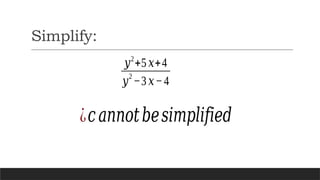The document explains operations involving rational algebraic expressions, including multiplication, division, addition, and subtraction, using the least common denominator. It also covers various factoring techniques such as the difference of squares, sum and difference of cubes, and perfect square trinomials, along with examples. Additionally, it discusses the simplification of rational expressions and provides group activities for practice.

1. Operations of
Rational
Algebraic
Expression

2. Multiplying Rational Algebraic
Expressions
The product of two rational expressions is the product of the
numerators divided by the product of the denominators. In
symbols,

3. Multiplying Rational Algebraic
Expressions
Find the product of
Express the numerators and denominators
into prime factors
¿
(5)(𝑡)(22
)
(2¿¿ 2)(2 )(3 𝑡 )𝑡 ¿
¿
5
( 2 ) ( 3 𝑡 )
¿
5
6 𝑡
Simplify rational expressions using laws of
exponents

4. Dividing Rational Algebraic
Expressions
The quotient of two rational expressions is the product of the
dividend and the reciprocal of the divisor.

5. Adding and Subtracting Dissimilar
Rational Algebraic Expressions
In adding or subtracting dissimilar rational expressions, change
the rational algebraic expressions into similar rational algebraic
expressions using the least common denominator or LCD and
proceed as in adding similar fractions

6. Adding and Subtracting Dissimilar
Rational Algebraic Expressions
Find the sum of

7. FACTORING
DIFFERENCE OF TWO SQUARES

8. Factoring Difference of Two
Squares
The factored form of a polynomial that is a
difference of two squares is the sum and
difference of the square roots of the first and
last terms.

9. Factoring Difference of Two
Squares
4 𝑥2
−36 𝑦2
h
𝑇 𝑒 𝑠𝑞𝑢𝑎𝑟𝑒𝑟𝑜𝑜𝑡 𝑜𝑓 4 𝑥2
𝑖𝑠2 𝑥
h
𝑇 𝑒 𝑠𝑞𝑢𝑎𝑟𝑒𝑟𝑜𝑜𝑡 𝑜𝑓 36 𝑦2
𝑖𝑠6 𝑦
(

10. Factor
𝑥2
− 9
√ 𝑥2
=𝑥
( 𝑥 + 3 )( 𝑥 − 3 )
9

11. Factor
𝑦 2
− 25
√ 𝑦2
=𝑦
( 𝑦 +5 )( 𝑦 − 5 )

12. Factor
4 𝑥2
−25
√4𝑥2
=2𝑥
(2 𝑥+5) (2 𝑥 − 5)

13. Factor
9 𝑏2
−100
√9𝑏2
=3𝑏
(3 𝑏 +10)(3 𝑏 −10)

14. FACTORING
SUM AND DIFFERENCE OF TWO CUBES

15. Factoring the Sum and Difference
of Two Cubes
The polynomial in the form is called the sum of two cubes because two
cubic terms are being added together.
That is:
The polynomial in the form is called the difference of two cubes because
two cubic terms are being deducted together.
That is:

16. Factor
27 𝑥3
+𝑦 3
3
√27𝑥3
=3𝑥
U sethe factorizationof ∑of cubes¿rewrite,that is
3
√𝑦3
=𝑦
= (𝑎 +𝑏)( 𝑎2
− 𝑎𝑏 + 𝑏2
)
(3 𝑥 + 𝑦 )(3 𝑥2
− 3 𝑥𝑦 + 𝑦2
)

17. Factor
𝑥3
+ 125
3
√𝑥3
=𝑥
U sethe factorizationof ∑of cubes¿rewrite,that is
3
√125=5
= (𝑎 +𝑏)( 𝑎2
− 𝑎𝑏 + 𝑏2
)
( 𝑥+ 5)( 𝑥2
− 5 𝑥+ 52
)
( 𝑥+ 5)( 𝑥2
− 5 𝑥+ 25)

18. Factor
𝑥3
+ 64
3
√𝑥3
=𝑥
U sethe factorizationof ∑of cubes¿rewrite,that is
3
√64=4
= (𝑎 +𝑏)( 𝑎2
− 𝑎𝑏 + 𝑏2
)
( 𝑥+ 4 )( 𝑥2
− 4 𝑥+ 42
)
( 𝑥+ 4 )( 𝑥2
− 4 𝑥+ 16)

19. Factor
𝑥3
− 27
3
√𝑥3
=𝑥
U sethefactorizationof differenceof cubes¿rewrite,thatis
3
√27=3
= (𝑎 − 𝑏)(𝑎2
+𝑎𝑏 + 𝑏2
)
( 𝑥 − 3)( 𝑥2
+3 𝑥 +32
)
( 𝑥 − 3)( 𝑥2
+3 𝑥 +9)

20. Factor
𝑥3
− 1
3
√𝑥3
=𝑥
U sethefactorizationof differenceof cubes¿rewrite,thatis
3
√1=1
= (𝑎 − 𝑏)(𝑎2
+𝑎𝑏 + 𝑏2
)
( 𝑥 − 1)( 𝑥2
+ 𝑥+12
)
( 𝑥 − 1)( 𝑥2
+ 𝑥+1 )

21. Factor
8 𝑥3
− 1000
3
√8 𝑥
3
=2𝑥
U sethefactorizationof differenceof cubes¿rewrite,thatis
3
√1000=10
= (𝑎 − 𝑏)(𝑎2
+𝑎𝑏 + 𝑏2
)
(2 𝑥 −10)(2 𝑥2
+2 𝑥 (10)+102
)
(2 𝑥 −10)(2 𝑥2
+20 𝑥+100)

22. FACTORING
PERFECT SQUARE TRINOMIAL AND
GENERAL TRINOMIAL

23. Perfect Square Trinomials
You can use the following relationships to factor perfect squares:

24. Factor
𝑥2
+16 𝑥+64
√ 𝑥2
=𝑥
U setherelationshipof perfectsquaretrinomials¿factor,thatis
√ 64=8
( 𝑥)2
+2 ( 𝑥 )(8 )+82
¿=¿
¿

25. Factor
4 𝑥2
−12 𝑥+9
√4𝑥2
=2𝑥
U setherelationshipof perfectsquaretrinomials¿factor,thatis
√ 9=3
(2 𝑥)2
−2 (2 𝑥 ) (3)+32
¿=¿
¿

26. Factor
𝑥2
+12 𝑥+36
√ 𝑥2
=𝑥
U setherelationshipof perfectsquaretrinomials¿factor,thatis
√ 36=6
( 𝑥)2
+2 ( 𝑥 )(6 )+62
¿=¿
¿

27. Factor
75 𝑥3
+30 𝑥2
+3 𝑥
√ 25 𝑥2
=5 𝑥 √ 1=1
(5 𝑥)2
+2 (5 𝑥) (1)+12
¿=¿
¿
75𝑥3
+30 𝑥2
+3 𝑥
3 𝑥
=3𝑥(25 𝑥
2
+10 𝑥+1)

28. Factor
75 𝑥3
+30 𝑥2
+3 𝑥
√ 25 𝑥2
=5 𝑥 √ 1=1
(5 𝑥)2
+2 (5 𝑥) (1)+12
¿=¿
¿
75𝑥3
+30 𝑥2
+3 𝑥
3 𝑥
=3𝑥(25 𝑥
2
+10 𝑥+1)

29. General Trinomials
To factor trinomials with 1 as the numerical coefficient of the leading term:
a. Factor the leading term of the trinomial and write these factors as the leading
terms of the factors;
b. List down all the factors of the last term;
c. Identify which factor pair sums up to the middle term; then
d. Write each factor in the pairs as the last term of the binomial factors.

30. Factor
𝑥2
−10 𝑥+21
List all factorsof 21that the∑will beequal¿−10
Factors Product Sum
7 3 21 10
1 21 21 22
-7 -3 21 -10
-1 -21 21 -22
Factors =
−7 −3

31. Factor
𝑥2
+5 𝑥 +6
List all factors of 6that the∑willbe equal ¿5
Factors Product Sum
2 3 6 5
6 1 6 7
-2 -3 6 -5
-6 -1 6 -7
Factors =
+2 +3

32. Factor
𝑧2
+4 𝑧 −21
List all factors of −21that the∑willbe equal¿ 4
Factors Product Sum
-3 7 -21 4
-7 3 -21 -4
-21 1 -21 -20
-1 21 -21 20
Factors =
−3 +7

33. Factor the expression using the Greatest Common Monomial Factor
Factor the Difference of Two Squares
3.
4.
Factor the Sum and Difference of Two Cubes
5.
6.
Factor the Perfect Square Trinomials
7.
8.
Factor the General Trinomials that has a leading coefficient 1
9.
10.

34. Rational
Algebraic
Expressions

35. Group Activity 1
1. The ratio of a number x and four added to two.
2. The product of the square root of three and the number y.
3. The square of a added to twice the a.
4. The sum of b and two less than the square of b.
5. The product of p and q divided by three.
6. One third of the square of c.
7. Ten times a number y increased by six.
8. The cube of a number z decreased by nine.
9. The cube root of nine less than a number w.
10. A number h raised to the fourth power.
1 2
3
4
5
6
7 8
9
10

36. Rational Algebraic Expressions
All polynomials are expressions but not all
expressions are polynomials.
A rational algebraic expression is a ratio of two polynomials provided
that the denominator is not equal to zero. In symbols: , where and are
polynomials and

37. Group Activity 2
RATIONAL ALGEBRAIC EXPRESSIONS NOT RATIONAL ALGEBRAIC EXPRESSIONS
IDENTIFY THE FOLLOWING EXPRESSIONS
𝑚 +2
0
𝑐4
𝑚− 𝑚
𝑦 + 2
𝑦 −2
𝑎
𝑦
2
− 𝑥
9
𝑘
3𝑘
2
− 6𝑘
1
𝑎
6
𝑐
𝑎 − 2
1− 𝑚
𝑚
3

38. Recall Laws of Exponents
I. Product of Powers
II. Power of a Power IV. Power of a Quotient
III. Power of a Product

39. Group Activity 3
REWRITE EACH EXPRESSIONS WITH POSITIVE EXPONENTS
1.
2.
3.
=
=
=

40. Simplifying
Rational
Algebraic
Expressions

41. Simplify:
4 𝑎+8𝑏
12
¿
𝑎+2𝑏
3
4 𝑎+8𝑏
12 ¿
4(𝑎+2𝑏)
4∙3
GCF = 4

42. Simplify:
15𝑐3
𝑑4
𝑒
12𝑐
2
𝑑
5
𝑤
¿
5 𝑐𝑒
4 𝑑𝑤
15𝑐3
𝑑4
𝑒
12𝑐
2
𝑑
5
𝑤 ¿
3∙5∙𝑐2
∙𝑐∙𝑑4
𝑒
3∙4∙𝑐
2
∙𝑑
4
∙𝑑∙𝑤
GCF = 3

43. Simplify:
𝑥2
+3 𝑥+2
𝑥
2
−1
¿
𝑥+2
𝑥 −1
¿
(𝑥+1)(𝑥+2)
(𝑥+1)(𝑥−1)
𝑥2
+3 𝑥+2
𝑥
2
−1

44. Simplify:
𝑦2
+5 𝑥+4
𝑦
2
−3 𝑥−4
¿𝑐𝑎𝑛𝑛𝑜𝑡𝑏𝑒𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑒𝑑

45. Simplify:
2𝑎+4𝑏
6
¿
𝑎+2𝑏
3
2𝑎+4𝑏
6 ¿
2(𝑎+2𝑏)
2∙3
1. 𝑥2
−9
𝑥
2
−7 𝑥+12
2.
𝑥2
−9
𝑥
2
−7𝑥+12 ¿
(𝑥+3)(𝑥−3)
(𝑥−4)(𝑥−3)
¿
(𝑥+3)
(𝑥− 4)