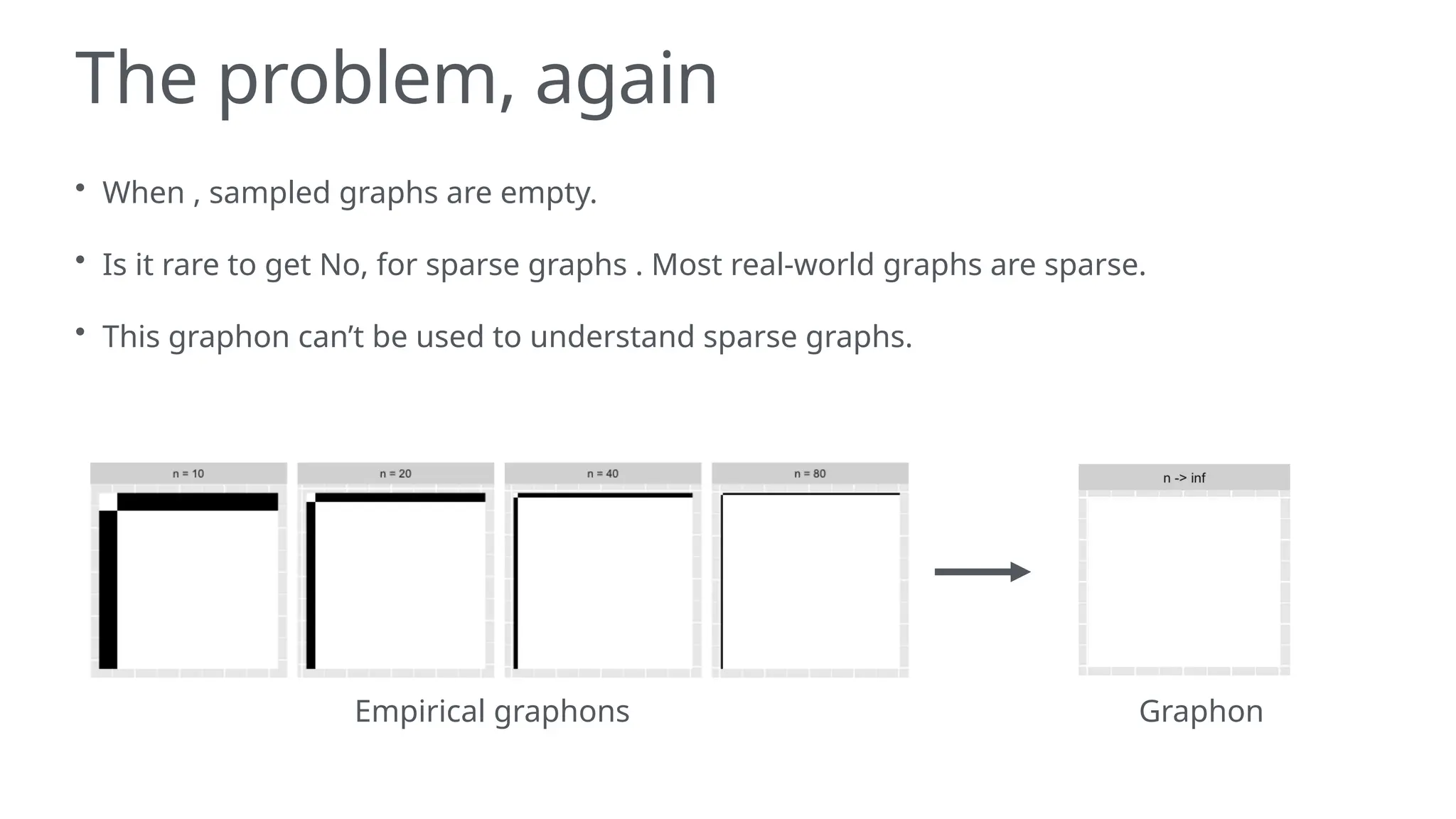
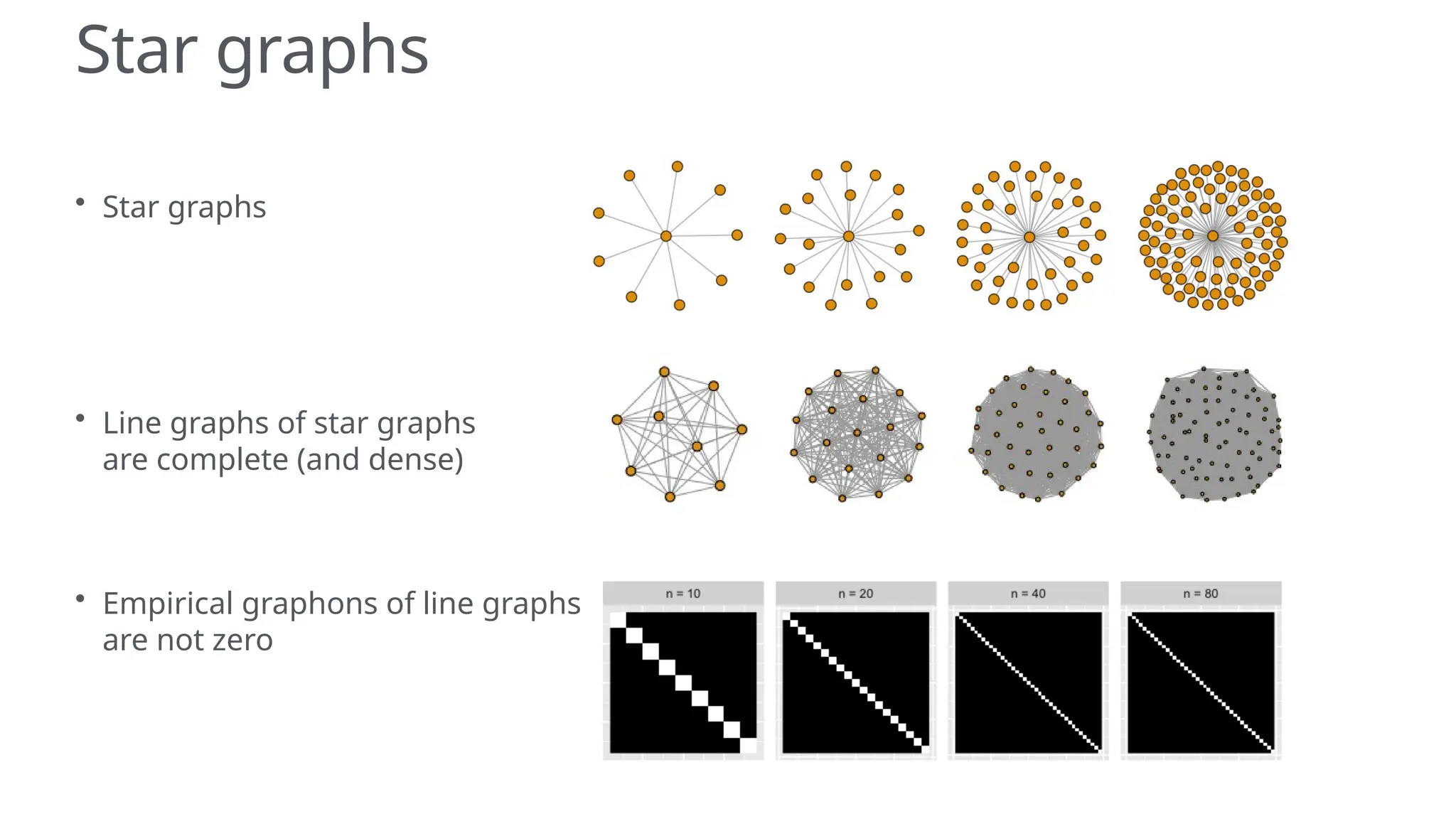
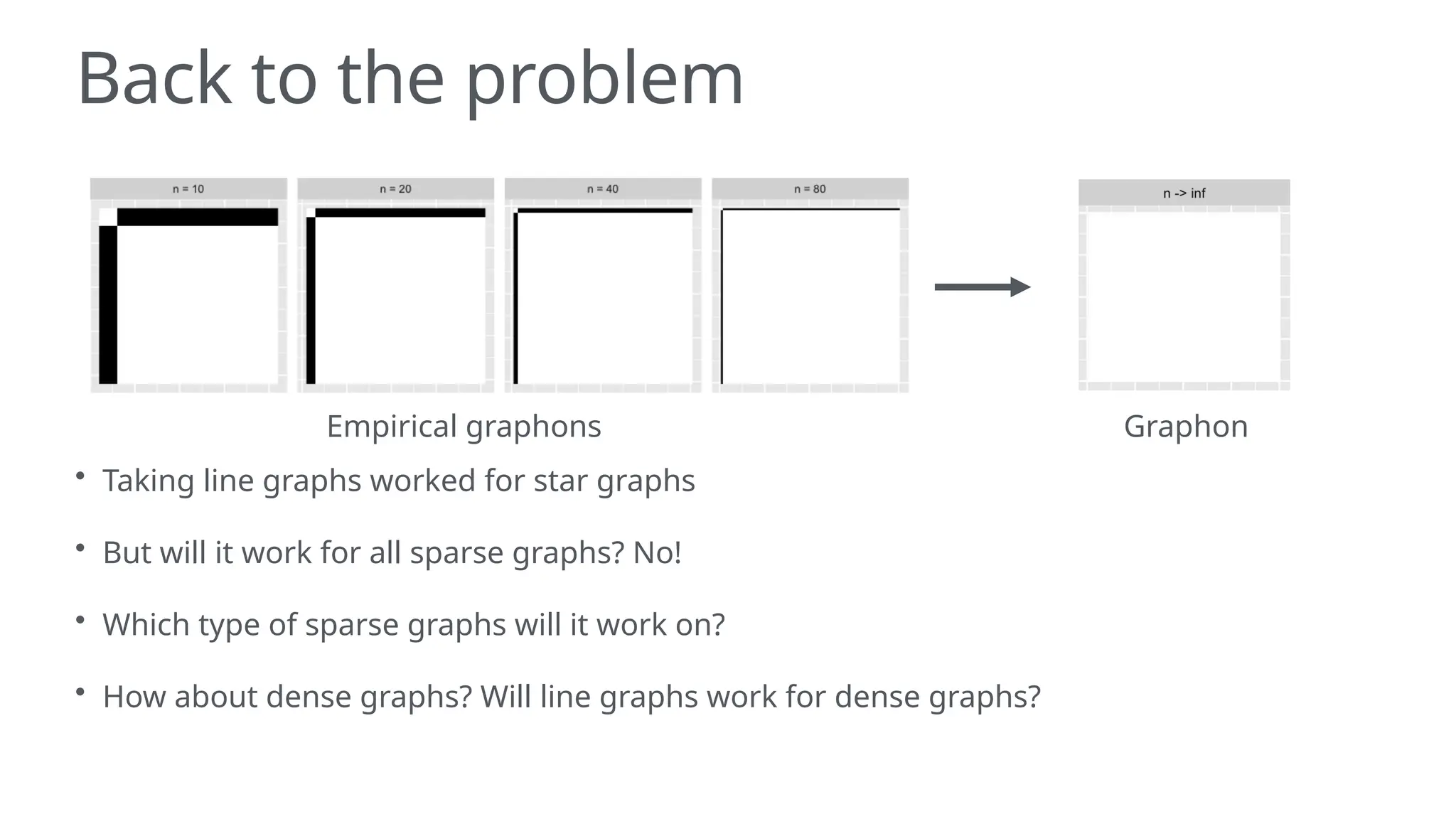
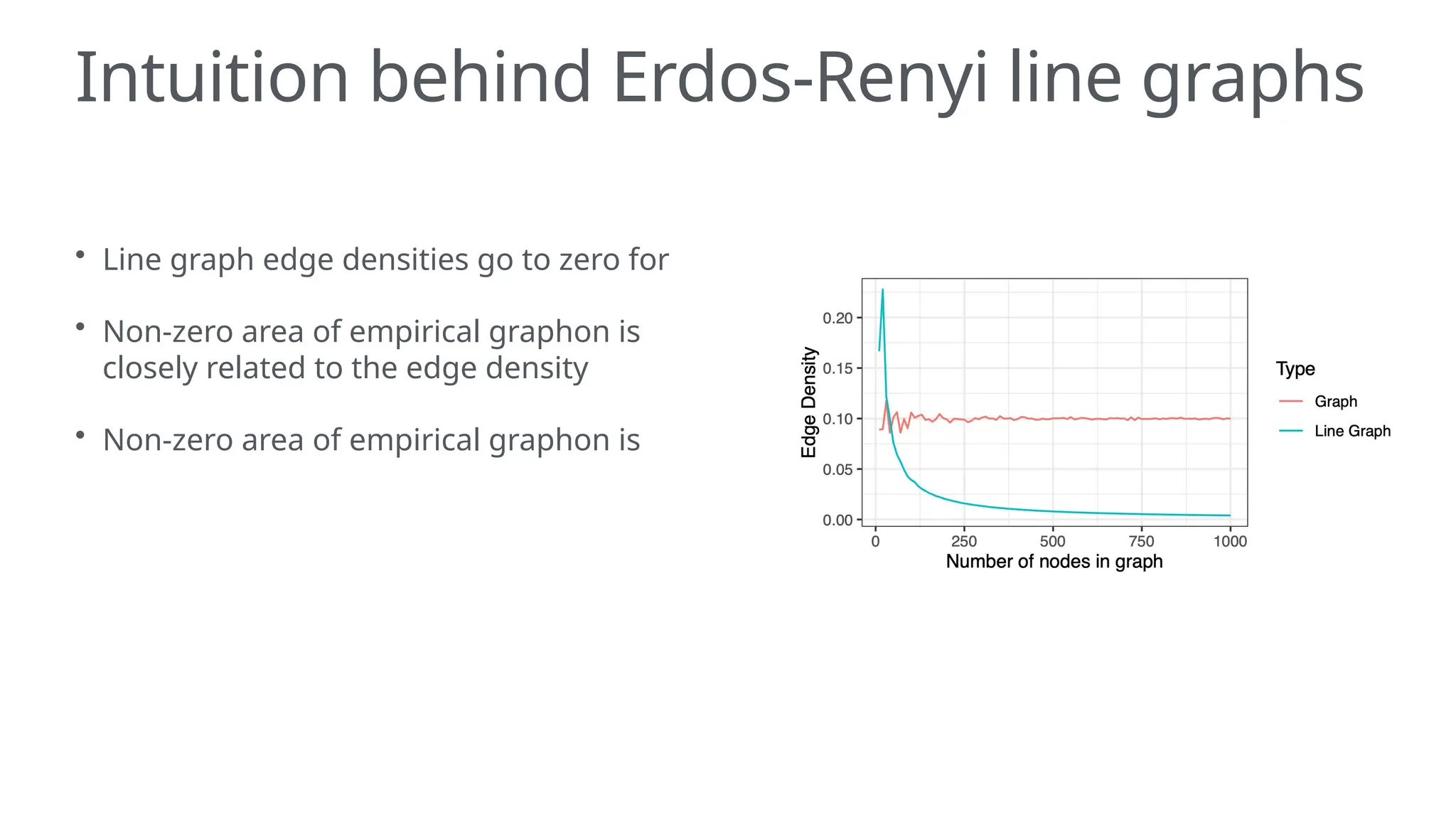
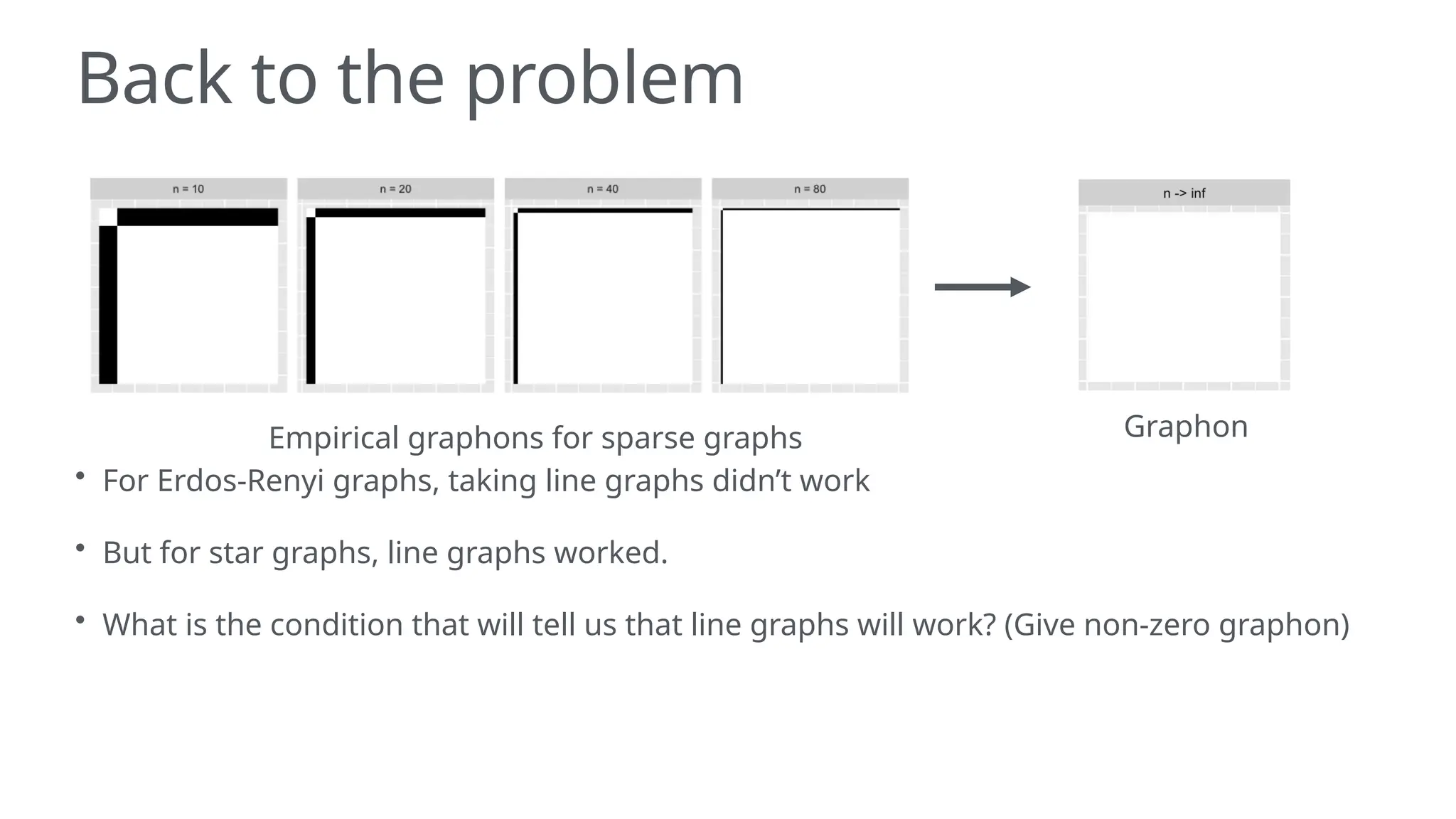
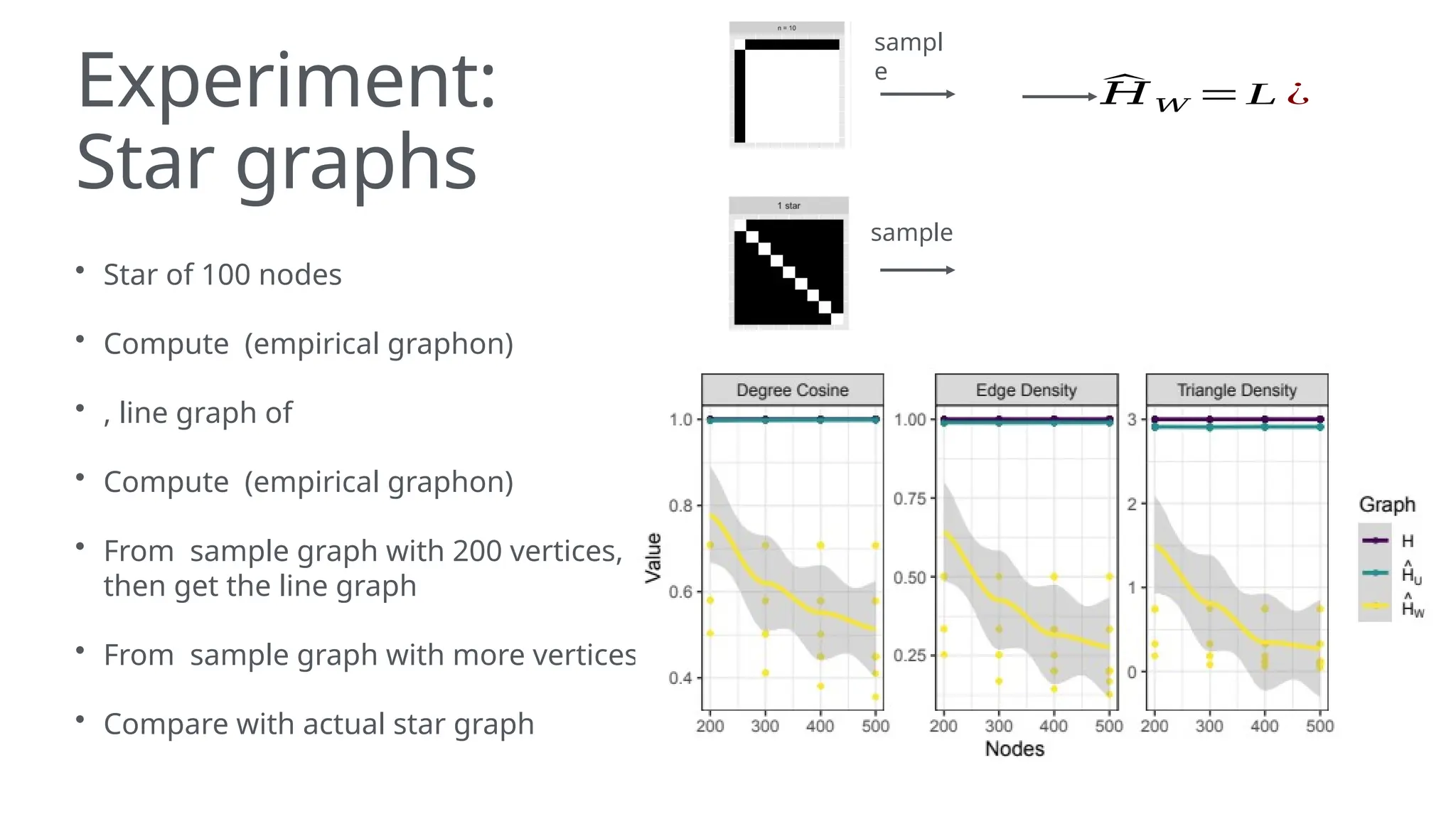
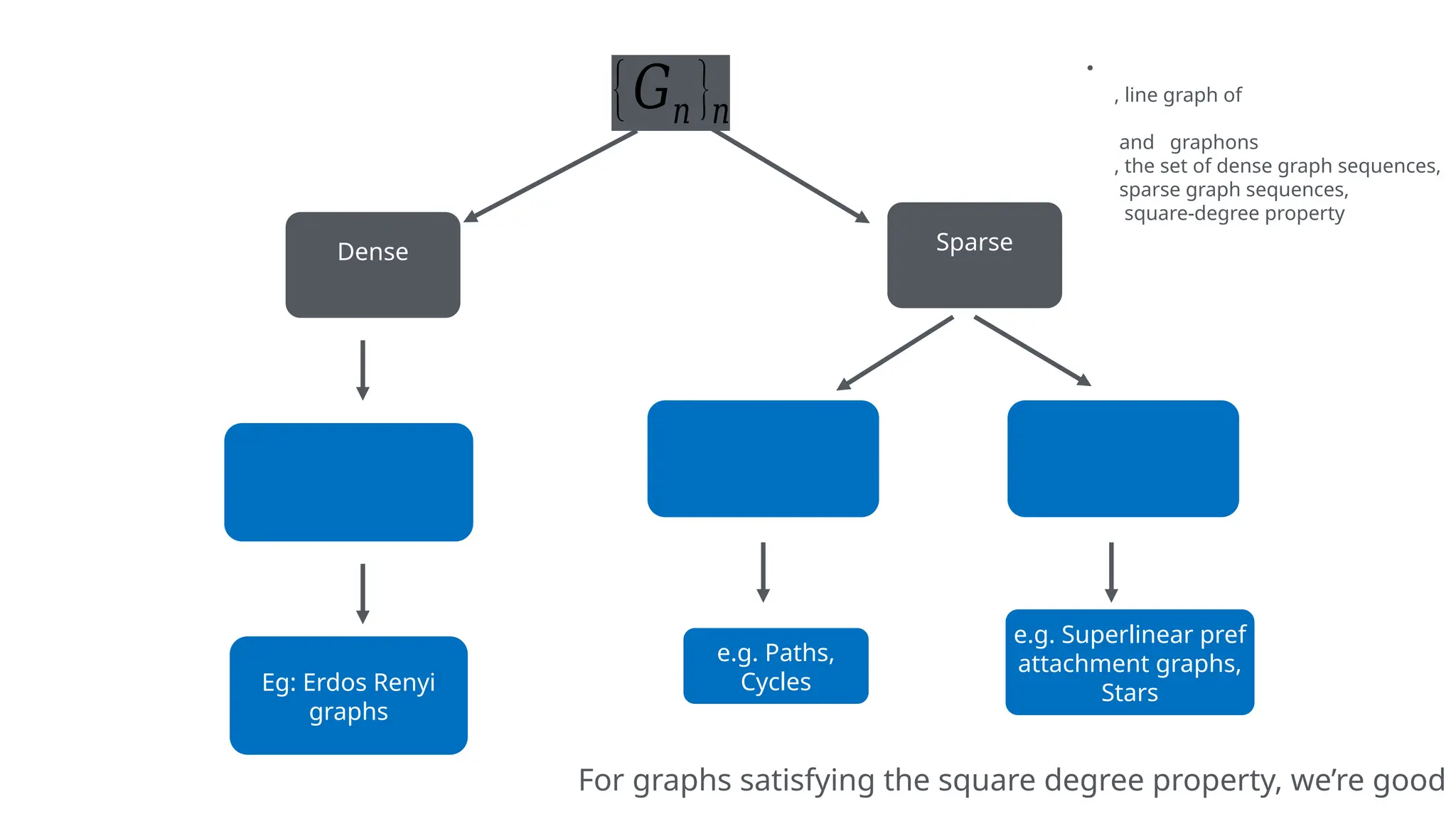
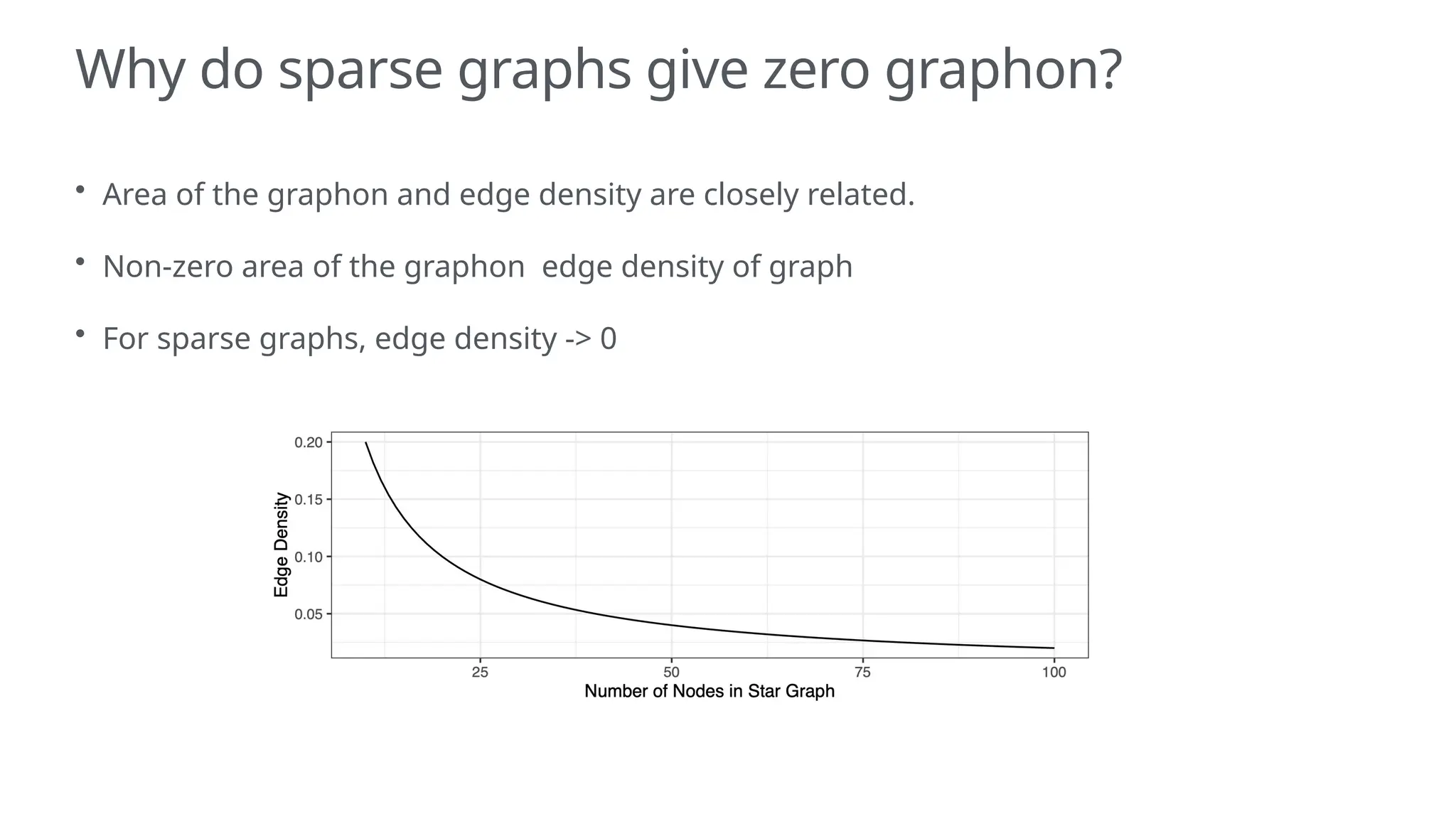
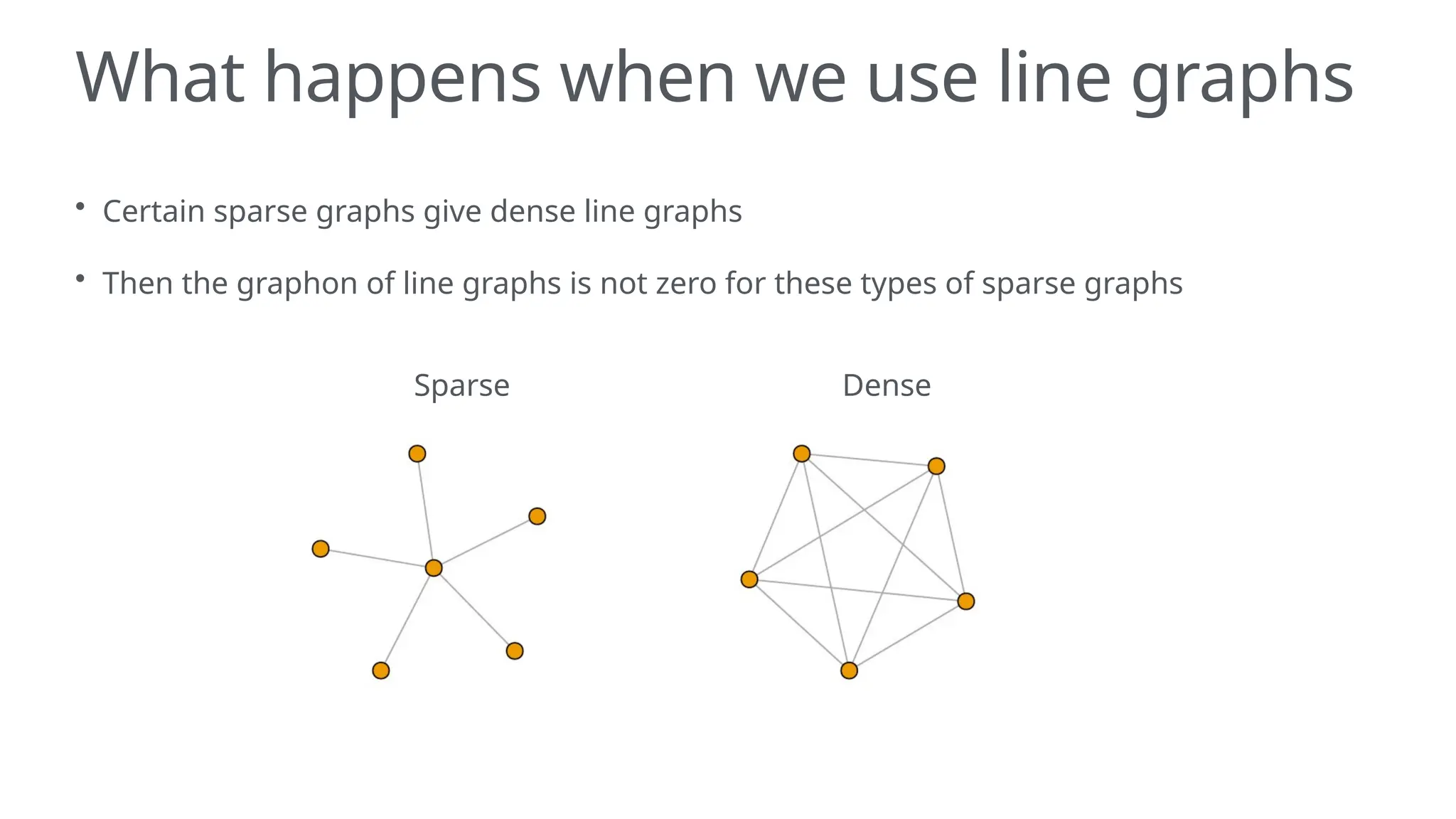
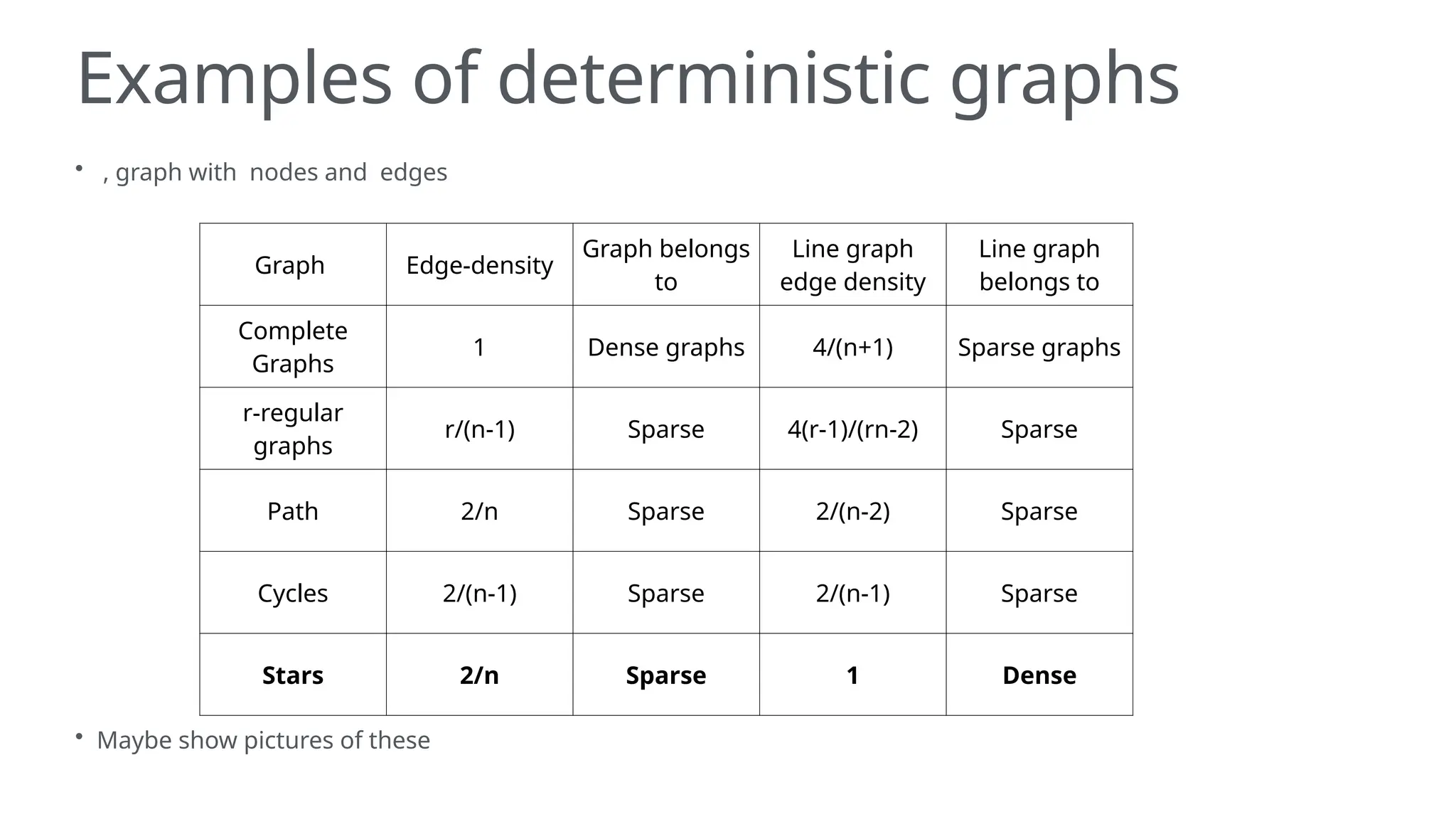
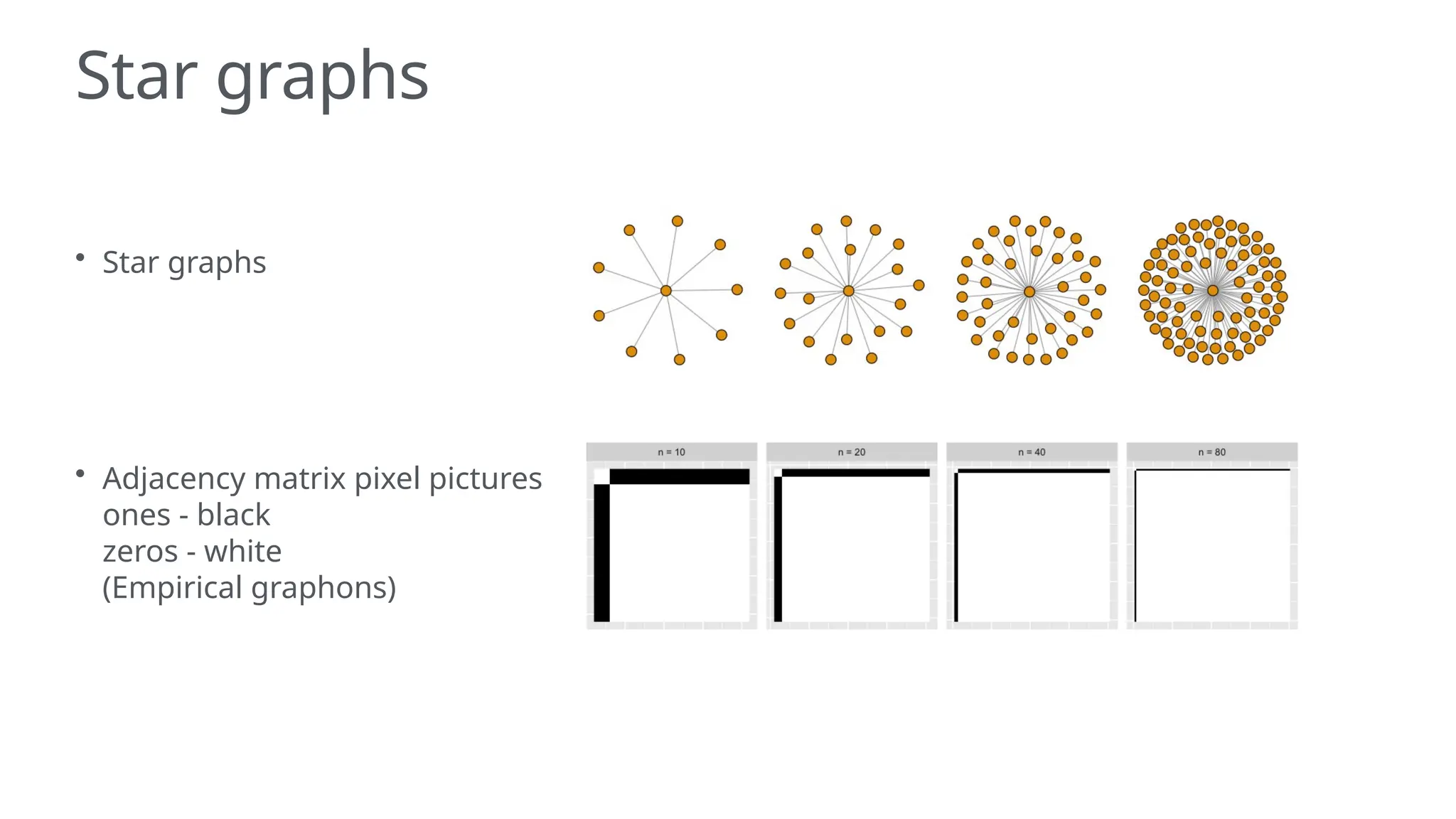
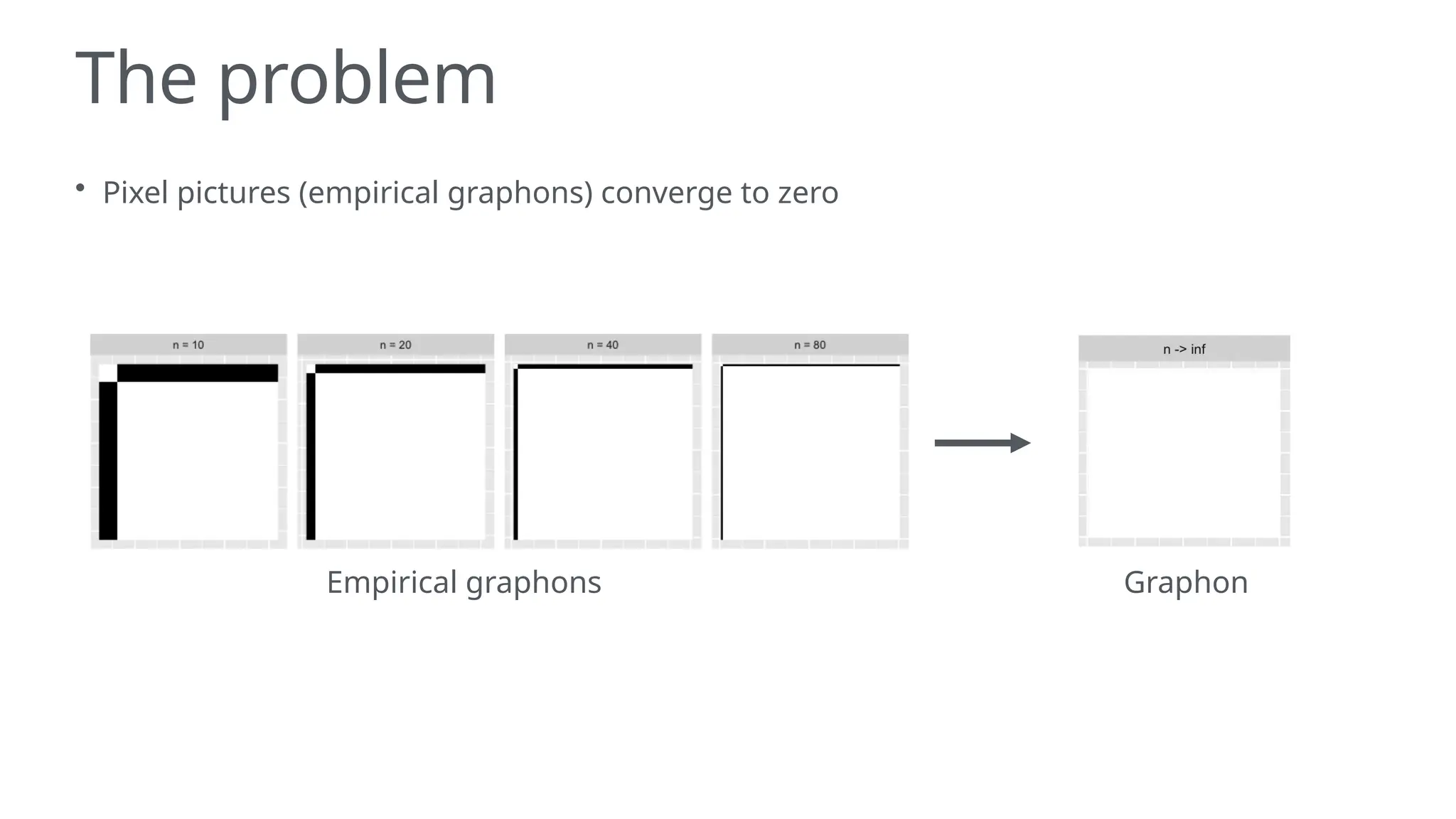
The document discusses graphons and their mathematical properties, specifically in relation to graph limits and the convergence of various types of graphs. It highlights the use of graphons to model social and computer networks, the conditions under which they work for dense and sparse graphs, and specifically examines the line graphs of star graphs and Erdos-Renyi graphs. The limitations of graphons in understanding sparse graphs and the implications of square-degree properties on graph density are also explored.

1. Statistics Seminar, University of Sydney, 30 September 2024
Sevvandi Kandanaarachchi, Cheng Soon Ong
CSIRO’s Data61
Graphons of Line Graphs

2. Growing graphs/networks
Social media networks
Career networks – LinkedIn
Grow over time
Computer networks – WWW
Graphons can be used to model these
networks if certain conditions are satisfied.
Graphons have nice mathematical properties.

3. Star graphs
• Star graphs
• Adjacency matrix pixel pictures
ones - black
zeros - white
(Empirical graphons)

4. The problem
• Pixel pictures (empirical graphons) converge to zero
Empirical graphons Graphon

5. What are graphons?
• Graph limits
• Examples from What is a graphon? By Daniel Glasscock
Erdos-Renyi graphs
Growing uniform attachment graphs
Bi-partite graphs

6. Mathematically what is a graphon?
• Graphon is a symmetric measurable function
• A function defined on a unit square
• Empirical graphon: when you colour in the squares of the adjacency matrix and scale it to
[0, 1]
• Empirical graphon of graph , is .
• Graphs converging to graphons
• How is convergence defined?
• Graph homomorphisms and homomorphism densities
Empirical graphons Graphon

7. Graph homomorphism - convergence
• A graph homomorphism from to is a map such that if then (Maps edges to edges). Let be
the set of all such homomorphisms and let . Then homomorphism density is defined as
•
• A graph sequence is said to be convergent if converges as goes to infinity for any simple
graph .

8. Convergence - cut metric
• The cut norm of a graphon is defined as where supremum is taken over all measurable
sets and of
• Given two graphons and , the cut metric is defined as
where is a measure preserving bijection from to .
• Why ? Because nodes can be re-named or permuted.
• Convergence in homomorphism density is equivalent to convergence in cut-metric. (Borgs
et al 2011)
• If a graph sequence converges (cut metric or hom. density) we have a graphon.

9. How can we use graphons?
• To generate new graphs (sample graphs)
• We can sample a graph with a larger number of nodes than currently seen - depicting the
graph at a future time point
• Suppose there are the nodes in your new graph
• Sample random numbers from the interval -
• For every consider the value of the graphon as a probability
• Toss a coin with probability , and connect the edge between and if you get heads
𝑟𝑖
𝑟 𝑗

10. The problem, again
• When , sampled graphs are empty.
• Is it rare to get No, for sparse graphs . Most real-world graphs are sparse.
• This graphon can’t be used to understand sparse graphs.
Empirical graphons Graphon

11. Dense and sparse graphs
• Consider a graph sequence , where has nodes and edges.
• Dense graphs:
• Edges grow quadratically with nodes
• Graph sequences with strictly positive edge-density limits
• Sparse graphs:
• Graph sequences with edge-density going to zero
• Edges grow subquadratically with nodes

12. Line graphs
• Edges Mapped to vertices
• Vertices are connected, if they share an edge
• The name line graphs - term came from
Frank Harary (motivated by Harary calling
“vertices" and “edges”, “points” and “lines”)
• Work originated by Hassler Whitney in
1932
• Other names used, interchange graphs,
edge-to-vertex dual, covering graph,
derivative, derived graph, adjoint,
conjugate
Graph Line graph

13. Star graphs
• Star graphs
• Line graphs of star graphs
are complete (and dense)
• Empirical graphons of line graphs
are not zero

14. Multiple stars
• Star graphs
• Line graphs of stars (complete subgraphs)
• Empirical graphons of line graphs

15. Back to the problem
• Taking line graphs worked for star graphs
• But will it work for all sparse graphs? No!
• Which type of sparse graphs will it work on?
• How about dense graphs? Will line graphs work for dense graphs?
Empirical graphons Graphon

16. Erdos-Renyi graphs
• Recall: dense graphs:
• For , this limit equals
• Theorem: Let be an Erdős–Rényi graph sampled from
a model and suppose has nodes and edges. Let
where denotes the line graph. As and go to infinity,
the edge density of satisfies
• This implies graphon of line graphs is zero for Erdos-
Renyi graphs.
Erdos-Renyi pixel pictures
and graphon
Line graphs of Erdos-Renyi graphs

17. Intuition behind Erdos-Renyi line graphs
• Line graph edge densities go to zero for
• Non-zero area of empirical graphon is
closely related to the edge density
• Non-zero area of empirical graphon is

18. Back to the problem
• For Erdos-Renyi graphs, taking line graphs didn’t work
• But for star graphs, line graphs worked.
• What is the condition that will tell us that line graphs will work? (Give non-zero graphon)
Empirical graphons for sparse graphs Graphon

19. Square-degree property
• (Sum of degree squares) (square of sum of degrees) for and
• Let denote a sequence of graphs. We say that exhibits the square-degree property if
there exists some and such that for all we have
• We denote the set of graph sequences satisfying the square-degree property by

20. Where does square-degree come from?
• Let the line graph of graph be denoted by , and has nodes and edges
• Then edge density of line graph density
•
• Square-degree property <=> line graph edge density is non-zero
<=> graphon of line graphs have non-zero area

21. What kind of graphs are square-degree?
• Sum of squares > c (square of sums) , where degrees are all positive as
• There has to be great disparity between the degrees
• Otherwise, the product terms will outweigh the square terms
• Graphs with hubs? How about stars?
• Stars , nodes and edges.
• and =>
• Stars satisfy the square-degree property

22. Experiment:
Star graphs
• Star of 100 nodes
• Compute (empirical graphon)
• , line graph of
• Compute (empirical graphon)
• From sample graph with 200 vertices,
then get the line graph
• From sample graph with more vertices
• Compare with actual star graph
^
𝐻𝑊 = L ¿
sampl
e
sample

23. {𝐺𝑛 }𝑛
Dense
Eg: Erdos Renyi
graphs
e.g. Paths,
Cycles
e.g. Superlinear pref
attachment graphs,
Stars
Sparse
•
, line graph of
and graphons
, the set of dense graph sequences,
sparse graph sequences,
square-degree property
For graphs satisfying the square degree property, we’re good

24. Map between and
• Say and where and and are graphons. , the set of dense graph sequences, sparse
graph sequences, square-degree property satisfying graph sequences

25. Bird’s-eye view
• Graphons for Sparse graphs
• Work by Caron and Fox
• Many methods led by Borgs and Chayes
• Work by Janson and others
• These methods have complex mathematical machinery
• Why? Because standard construction for sparse graphs give graphons with point masses
with measure zero
• The difference in our work
• Line graphs enable us to use the standard path for dense graphons

26. Thank you!
Preprint:
https://web3.arxiv.org/
abs/2409.01656

27. Extra slides

28. ∑ deg 𝑣𝑖 ,𝑛
2
≥ 𝑐1 ( ∑ deg 𝑣𝑖 , 𝑛 )2
• Say vertex degrees are given by then
• Want
• Intuition: this can only happen when some degrees are very very big compared to others.
• Mixed terms on RHS need to be smaller than the squares on the LHS
• Examples: superlinear preferential attachment graphs and stars

29. Limitations of the graphon
• Graphs sampled from the graphon are either dense or empty graphs (consequence of
Aldous-Hoover theorem)
• If non-zero area of graphon > 0
• Sampled graphs are dense
• If non-zero area of graphon = 0 (graphon )
• Graphs are empty

30. Existing work on sparse graphs
• Work by Caron and Fox
• Kallenberg exchangeability and Levy measures
• Many methods led by Borgs and Chayes
• Rescaled and stretched graphons, Graphexes
• Work by Janson and others
• Edge exchangeable graphs
• These methods have complex mathematical machinery

31. How does the graphon come in?
• Theorem (Borgs et al. 2008)
• converges iff there is a such that .
• And for every there is a convergent sequence of graphs like above.
Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T., & Vesztergombi, K. (2008). Convergent sequences of
dense graphs I: Subgraph frequencies, metric properties and testing. Advances in Mathematics,
219(6), 1801–1851. https://doi.org/10.1016/j.aim.2008.07.008

32. Why do sparse graphs give zero graphon?
• Area of the graphon and edge density are closely related.
• Non-zero area of the graphon edge density of graph
• For sparse graphs, edge density -> 0

33. What happens when we use line graphs
• Certain sparse graphs give dense line graphs
• Then the graphon of line graphs is not zero for these types of sparse graphs
Sparse Dense

34. Square-degree graphs are sparse
• This implies (definition of Sparse)

35. Are all sparse graphs square-degree?
• No! Paths, Cycles, r-regular graph sequences.
• If is dense, then
Dense
graphs Square-
degree
Sparse graphs

36. Square-degree result
• Theorem: Let be a sparse graph sequence. Let be the corresponding sequence of line
graphs with . Then , i.e., satisfies if and only if is dense.
• - the set of sparse graph sequences
• - the set of square-degree graph sequences
• - the set of dense graph sequences
• - square-degree condition

37. Examples of deterministic graphs
• , graph with nodes and edges
• Maybe show pictures of these
Graph Edge-density
Graph belongs
to
Line graph
edge density
Line graph
belongs to
Complete
Graphs
1 Dense graphs 4/(n+1) Sparse graphs
r-regular
graphs
r/(n-1) Sparse 4(r-1)/(rn-2) Sparse
Path 2/n Sparse 2/(n-2) Sparse
Cycles 2/(n-1) Sparse 2/(n-1) Sparse
Stars 2/n Sparse 1 Dense

38. Preferential Attachment Graphs
• New nodes connect to more connected nodes
• The probability that a new node connects to node , which has degree is given by
• Maximum degree
• Three regimes of : sublinear , linear , and superlinear
• Sethuraman & Venkataramani (2019) show that for ,
Sethuraman, S., & Venkataramani, S. C. (2019). On the Growth of a Superlinear Preferential Attachment Scheme. Springer Proceedings in Mathematics
and Statistics, 283, 243–265. https://doi.org/10.1007/978-3-030-15338-0_9

39. Superlinear pref. attachment
• Using this result we show
• Lemma: Let denote a sequence of graphs growing by superlinear preferential
attachment with . Then almost surely.
• Say and where and and are graphons.
• If is a superlinear pref. attachment graph sequence, then

40. Thank you!