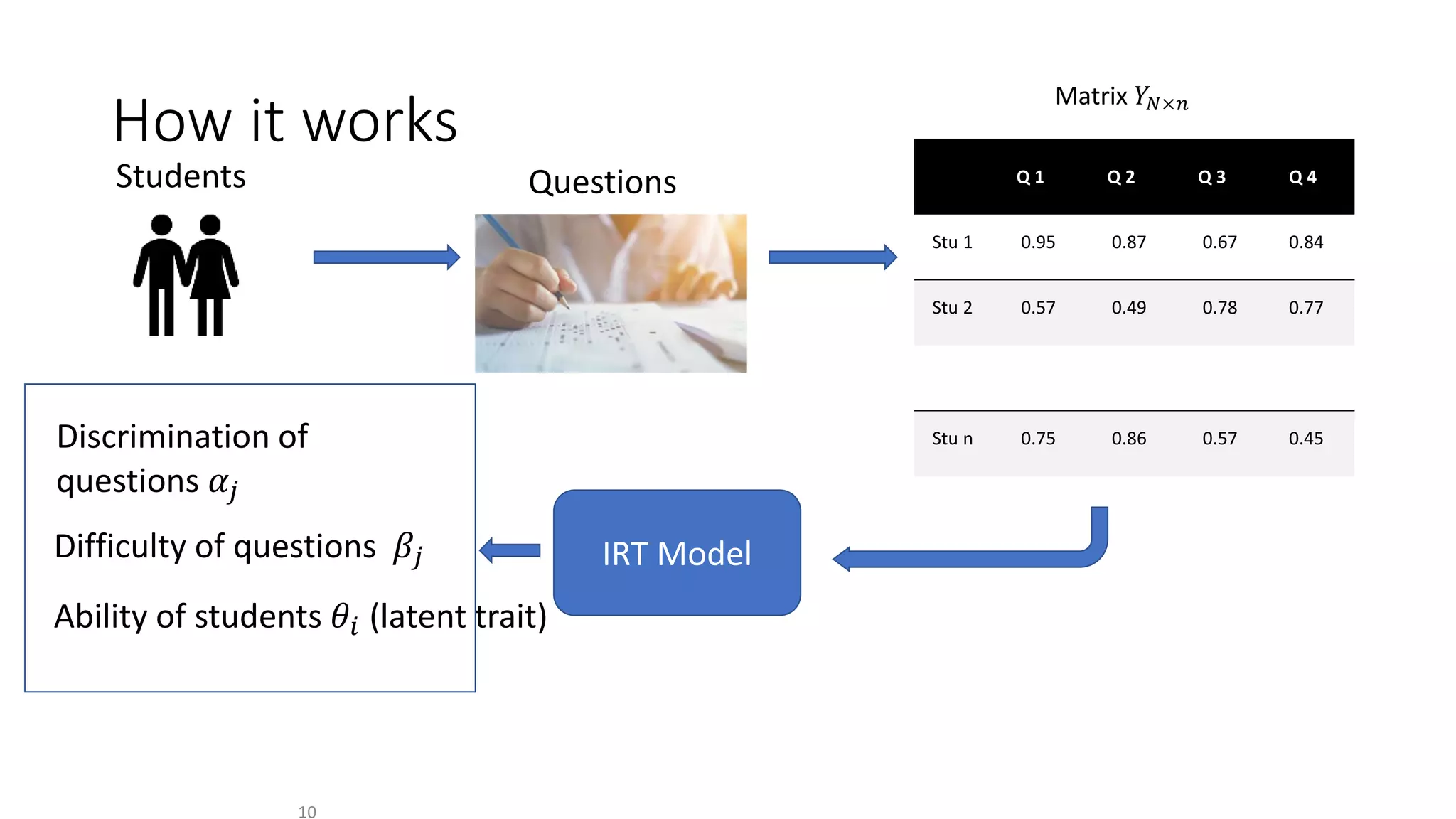
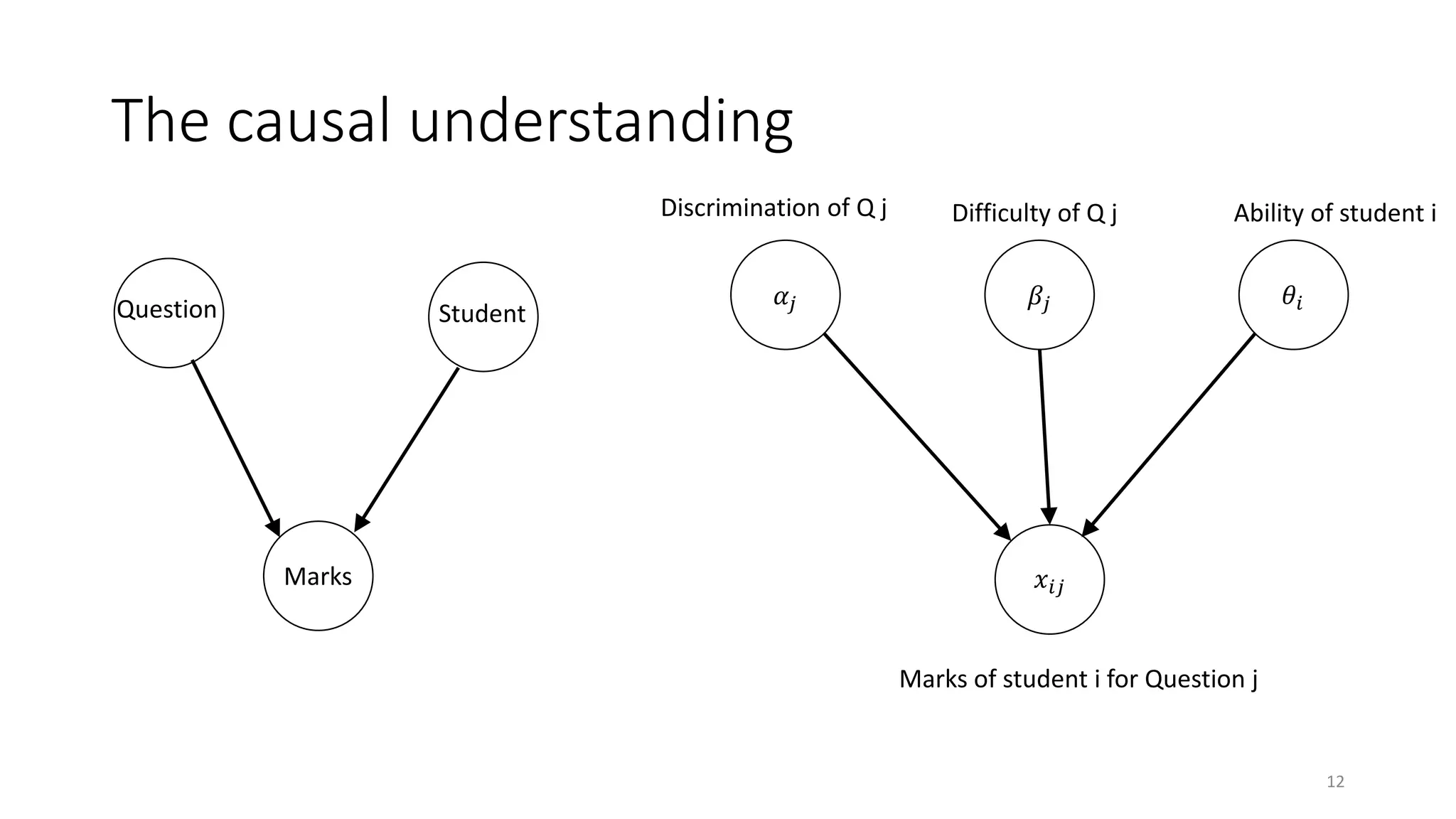
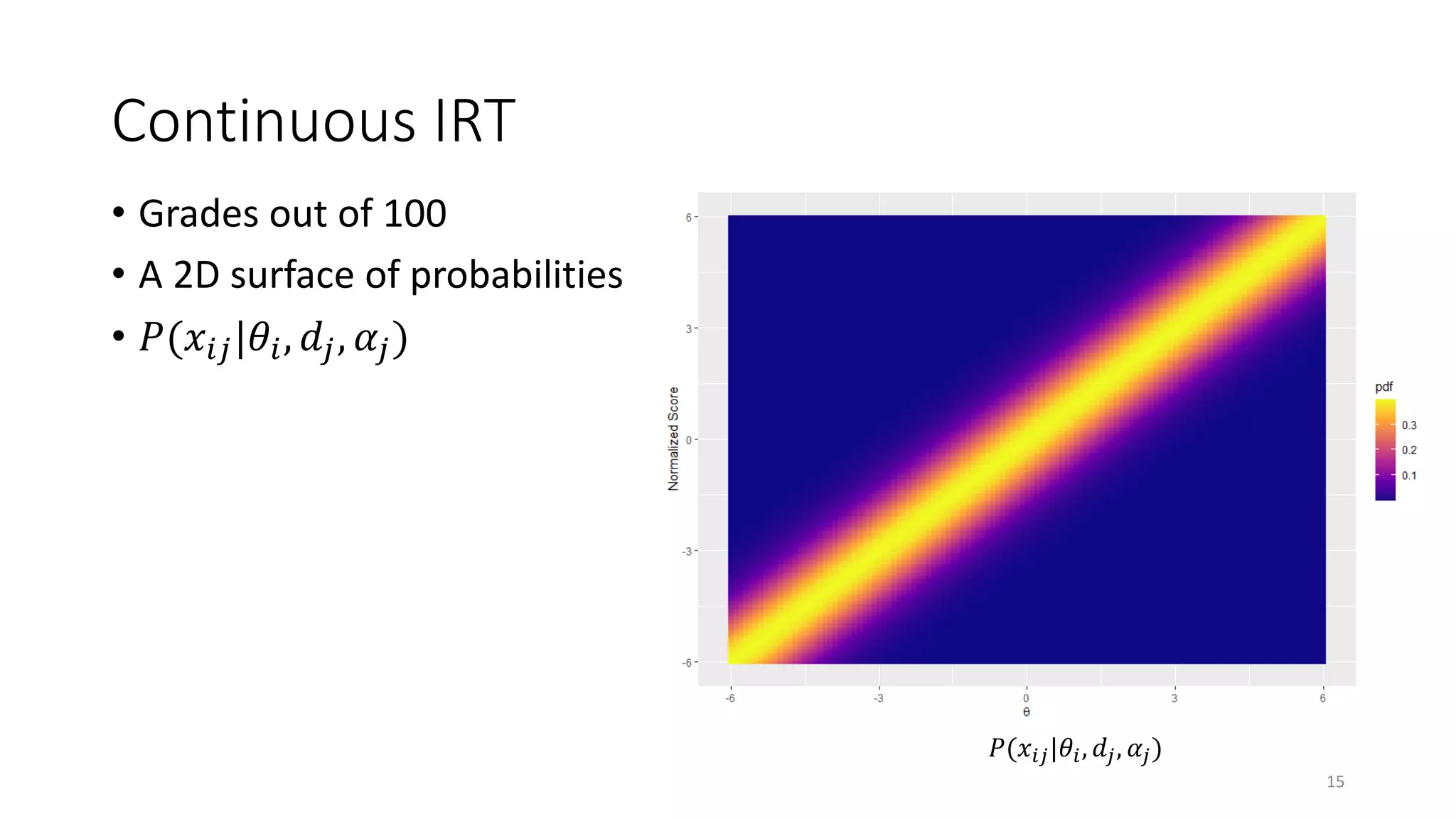
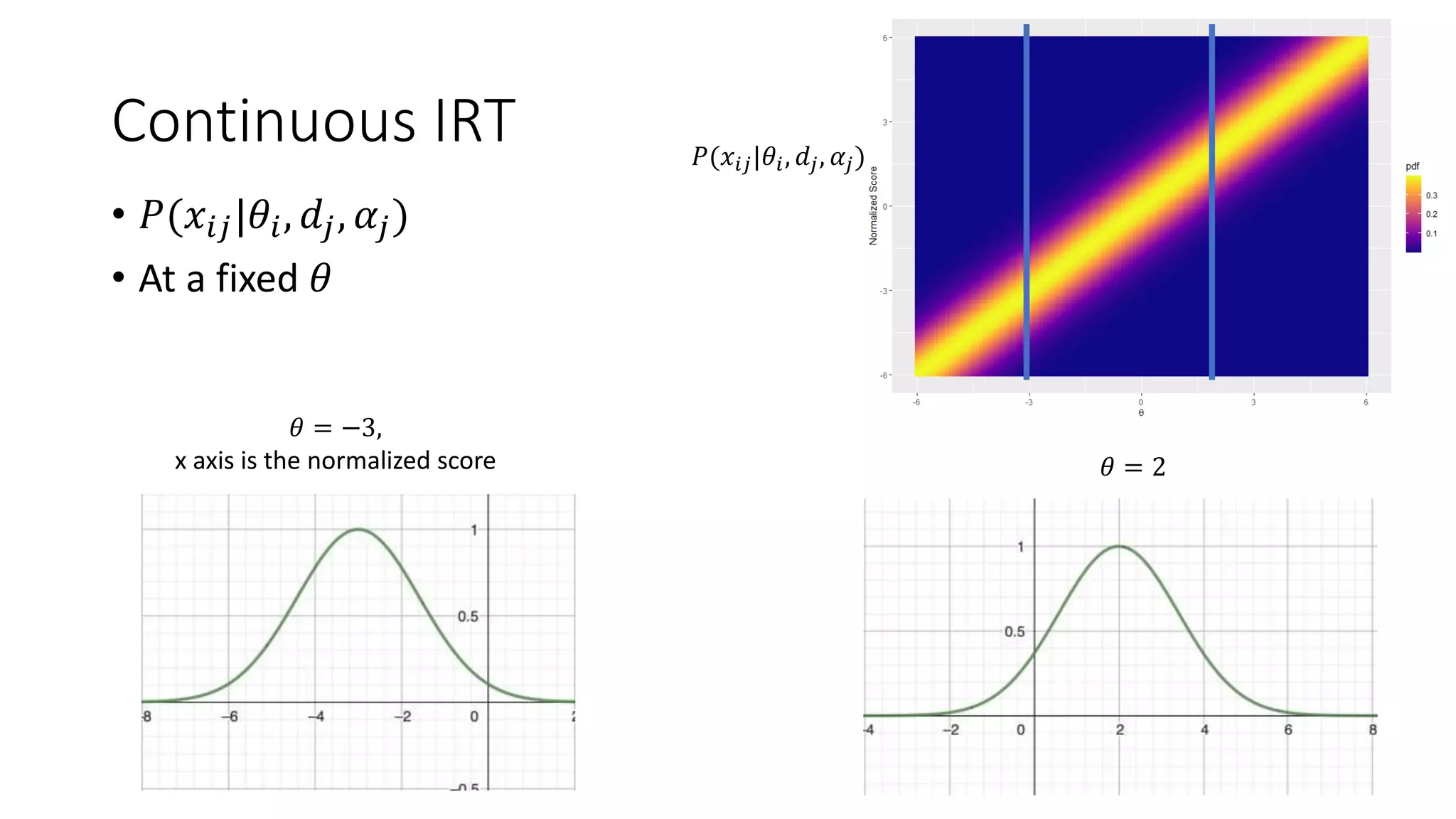
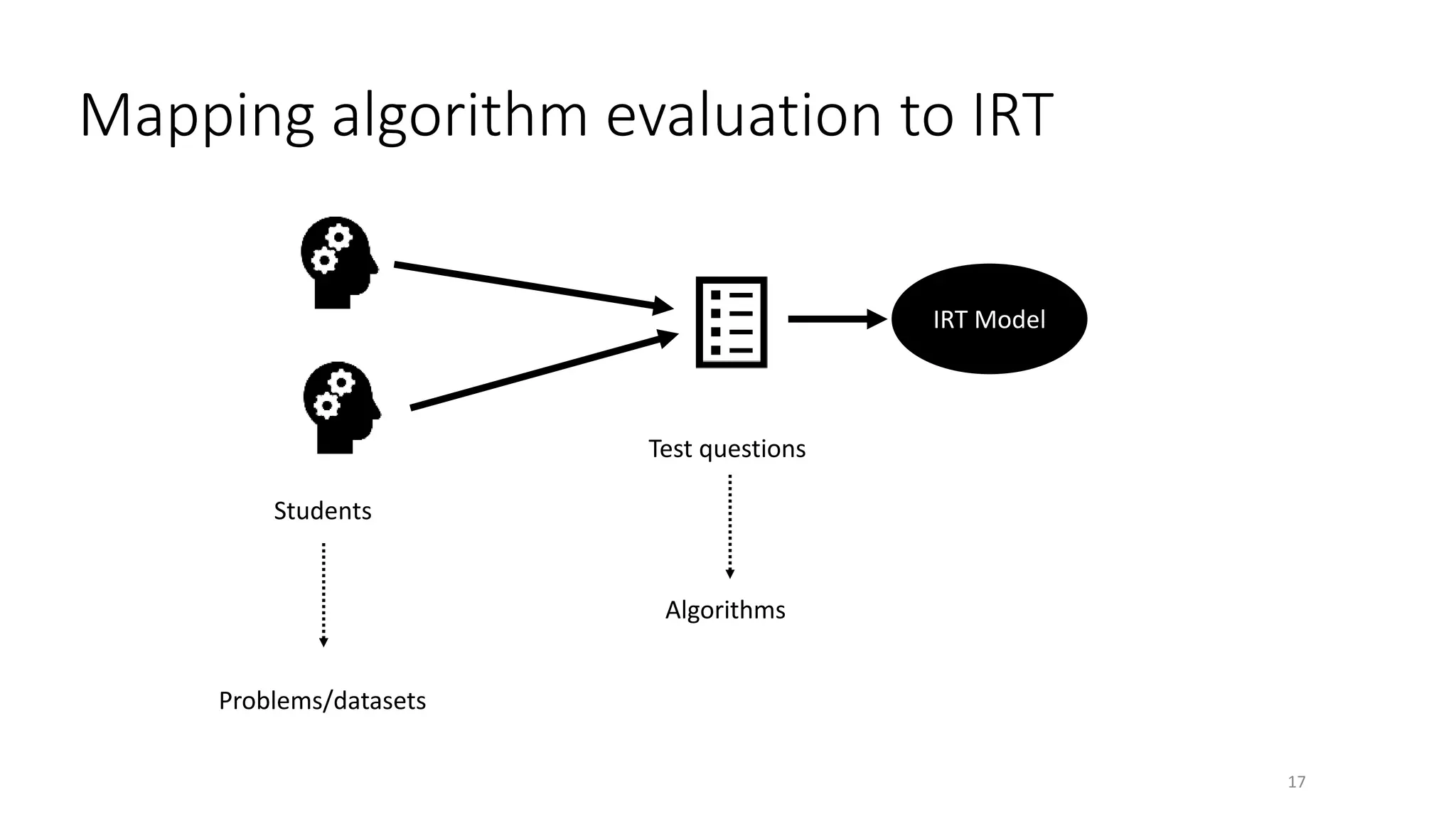
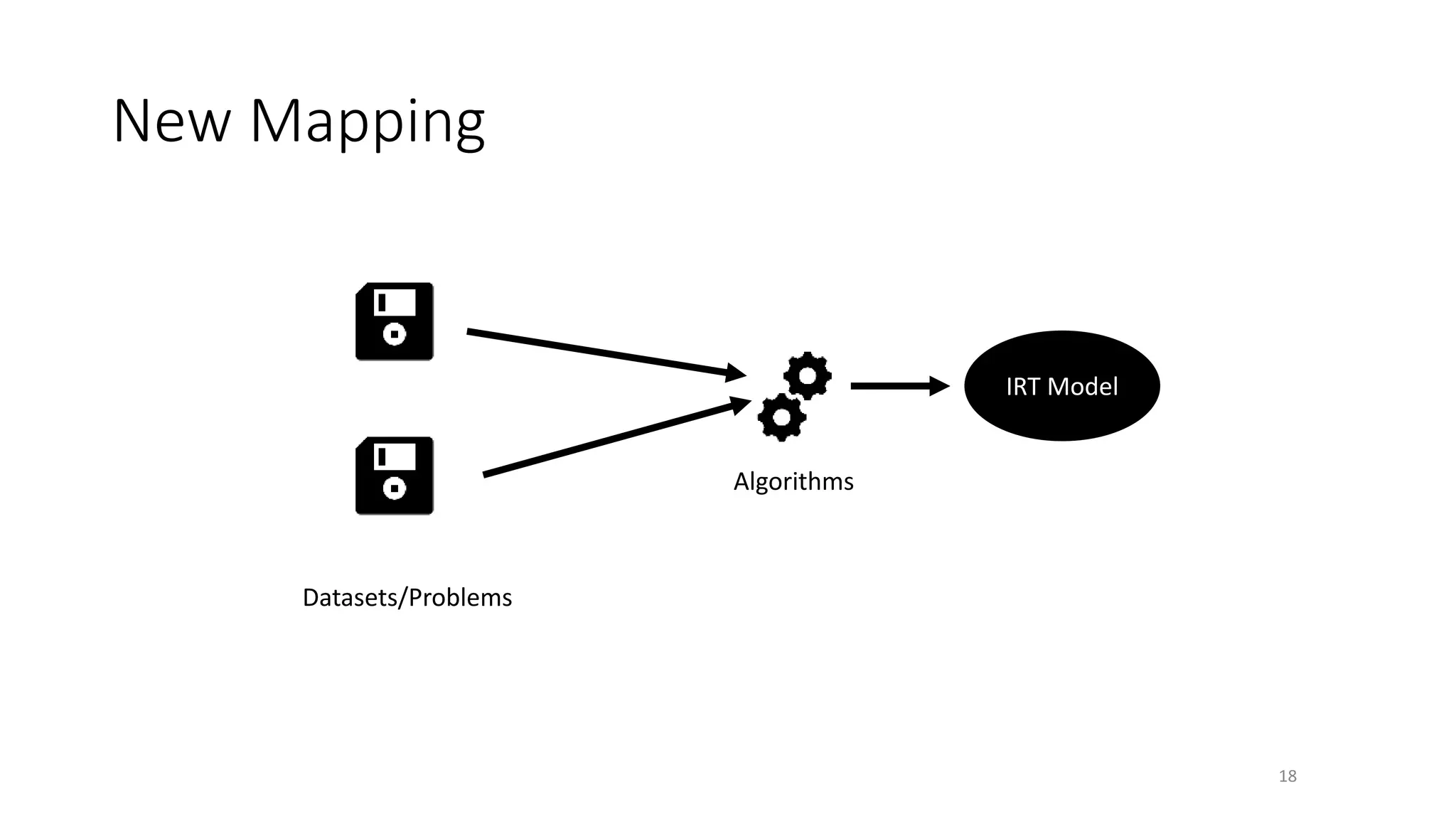
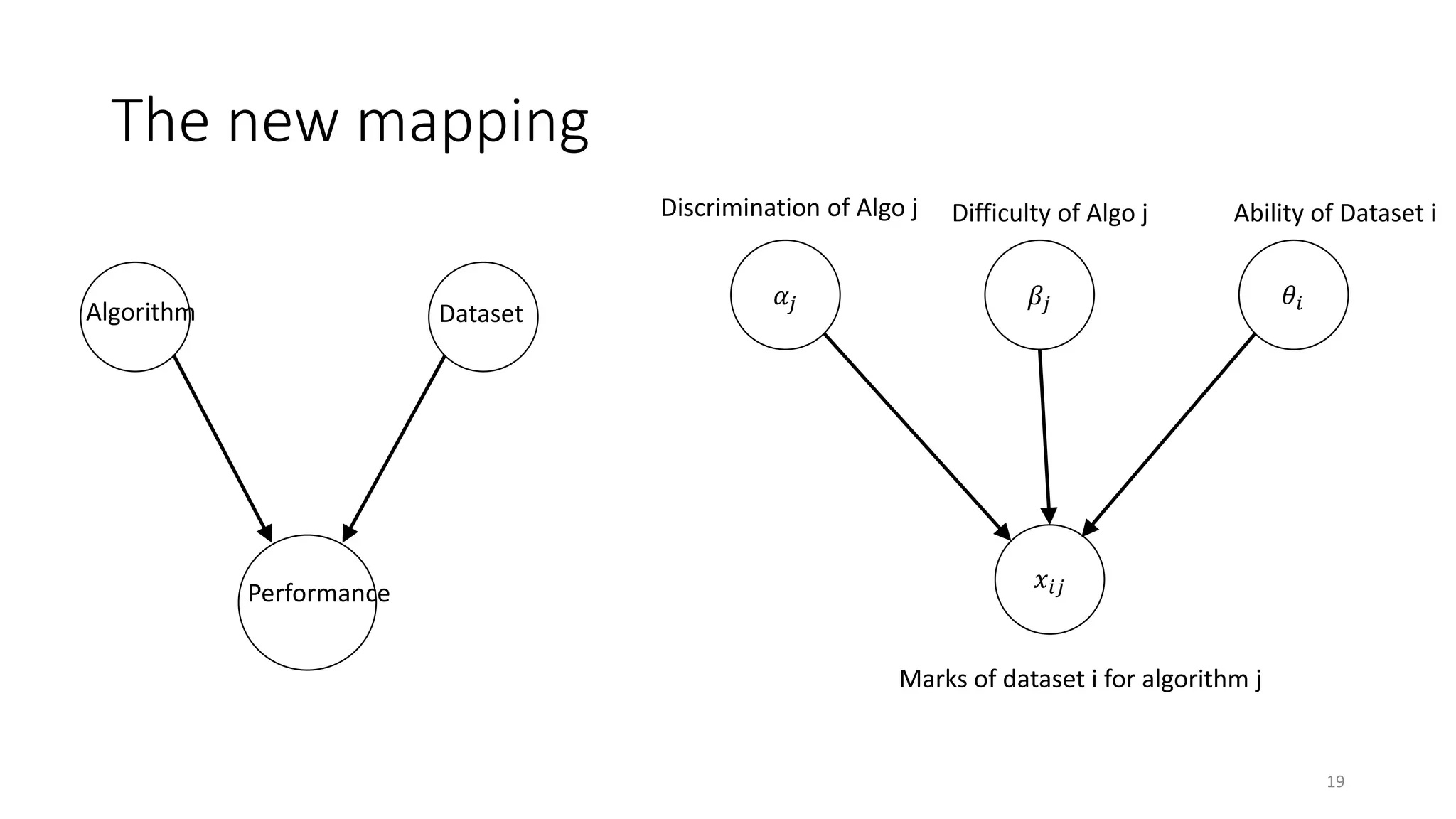
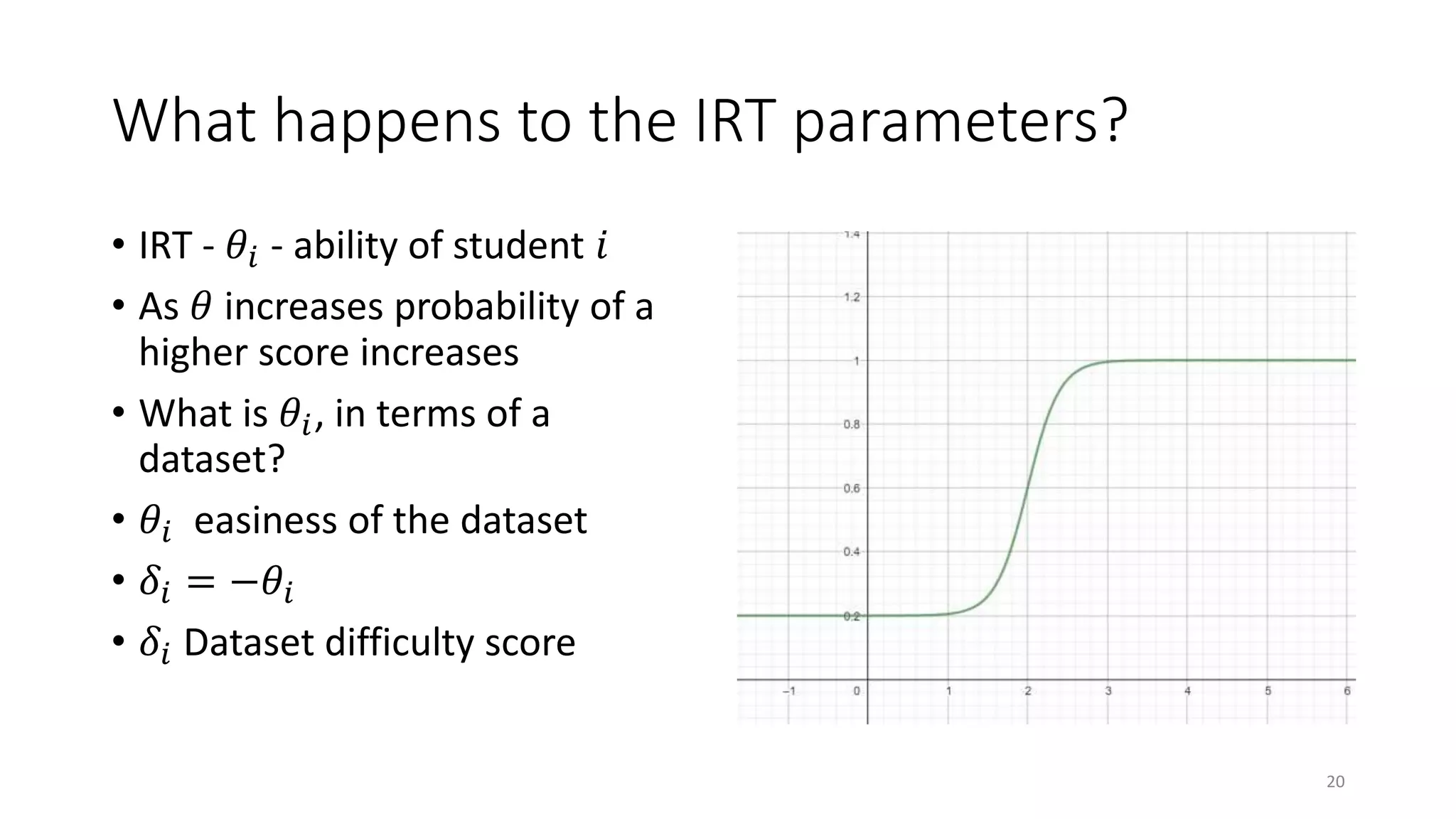
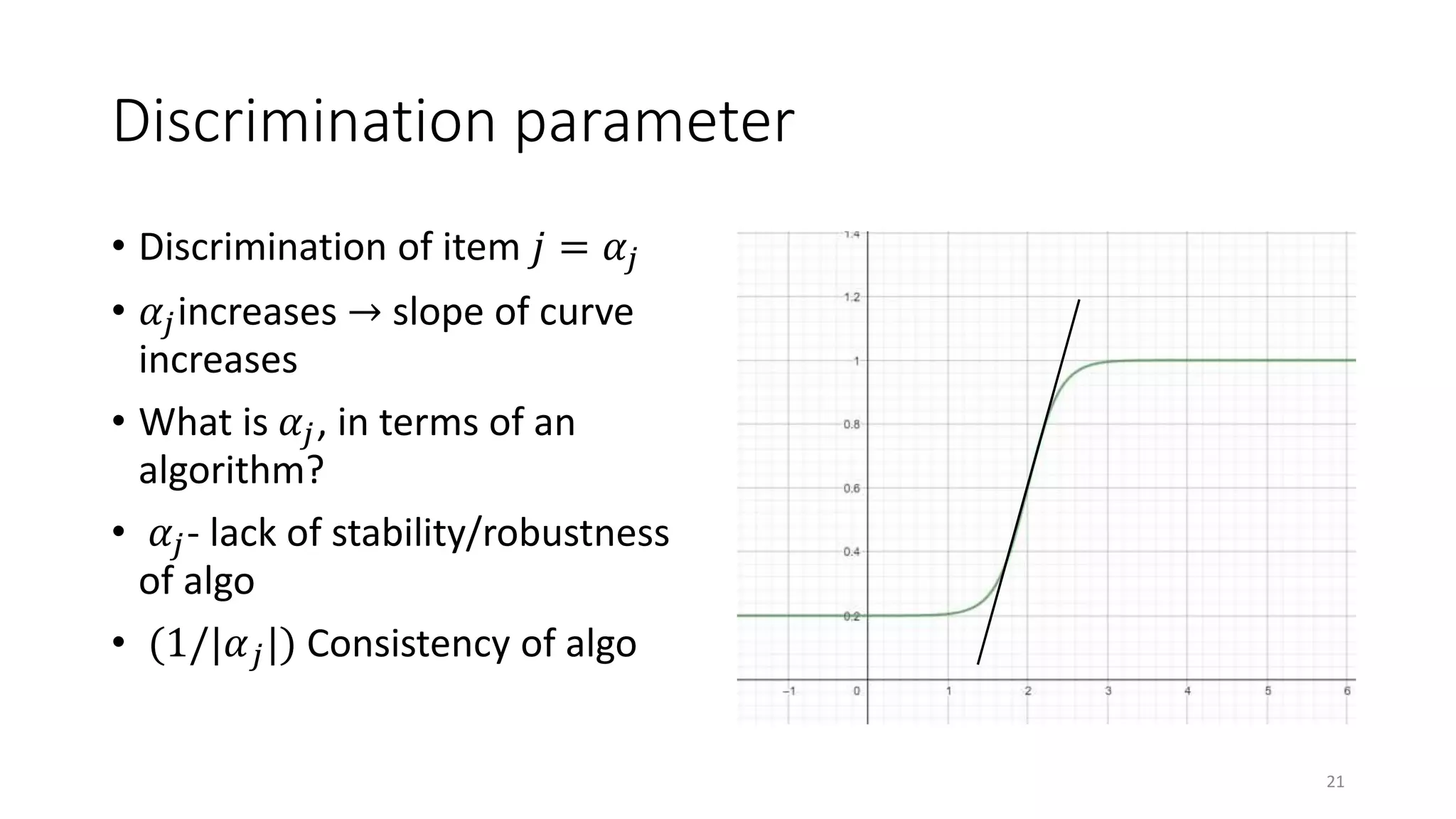
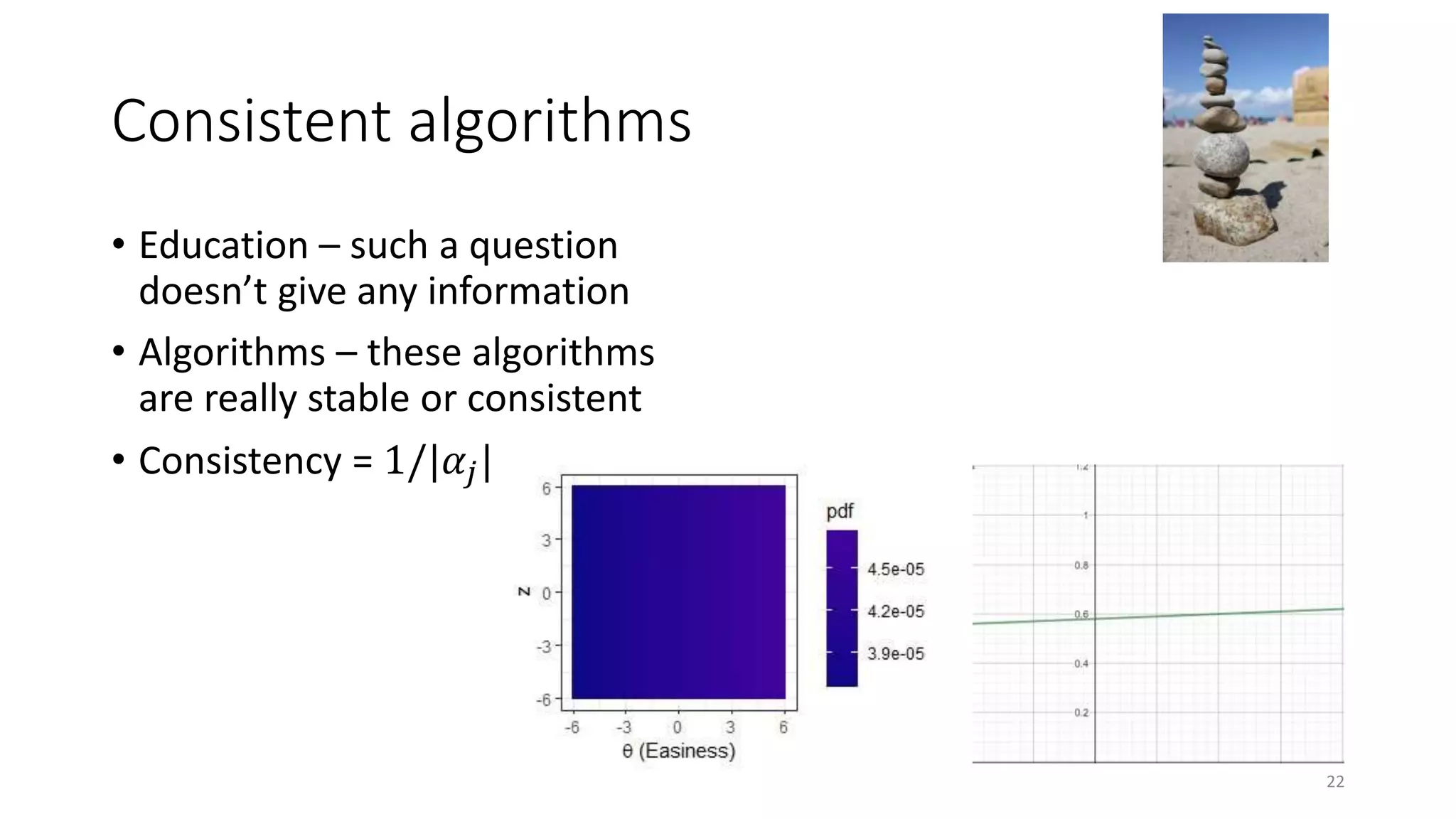
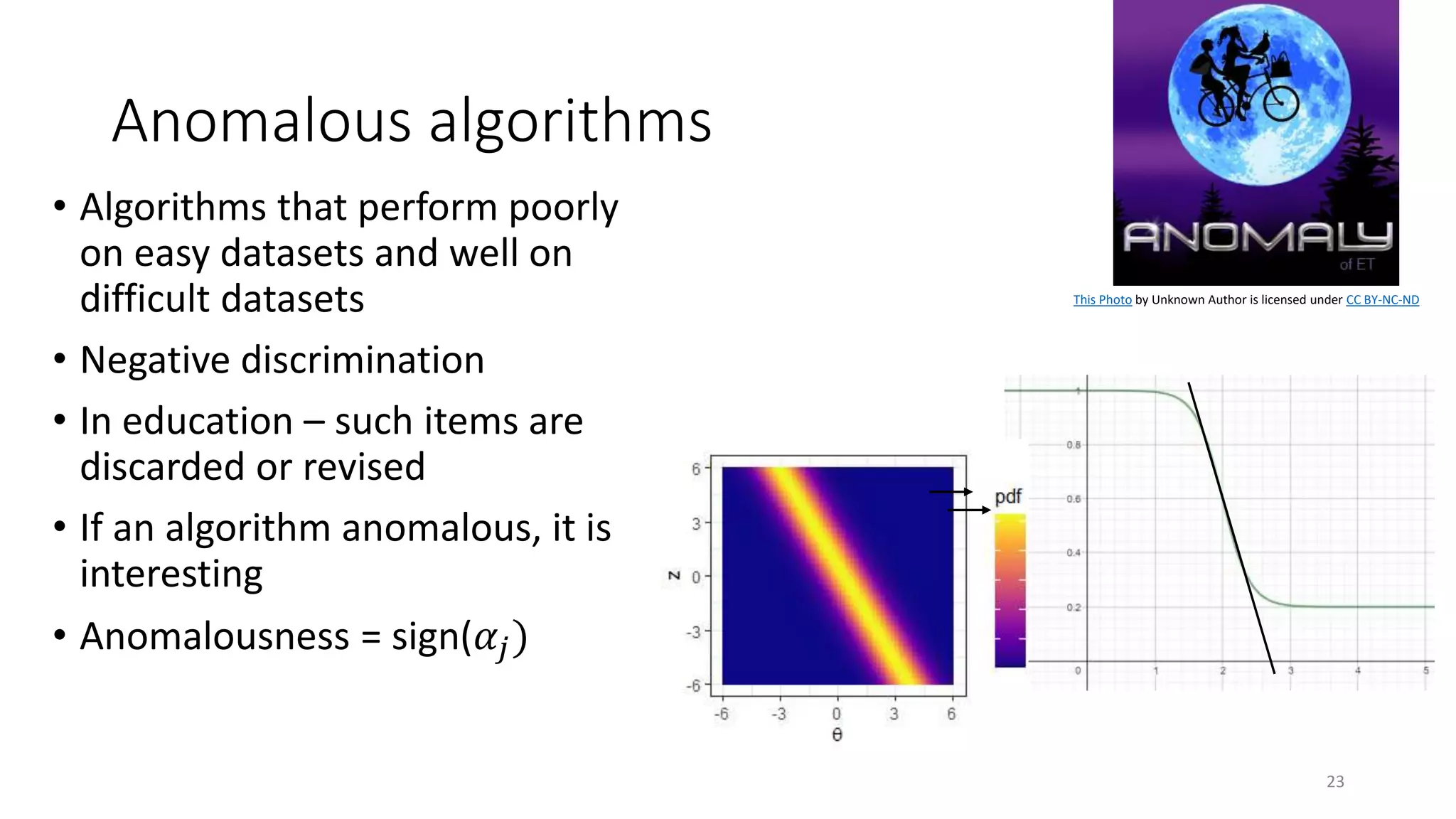
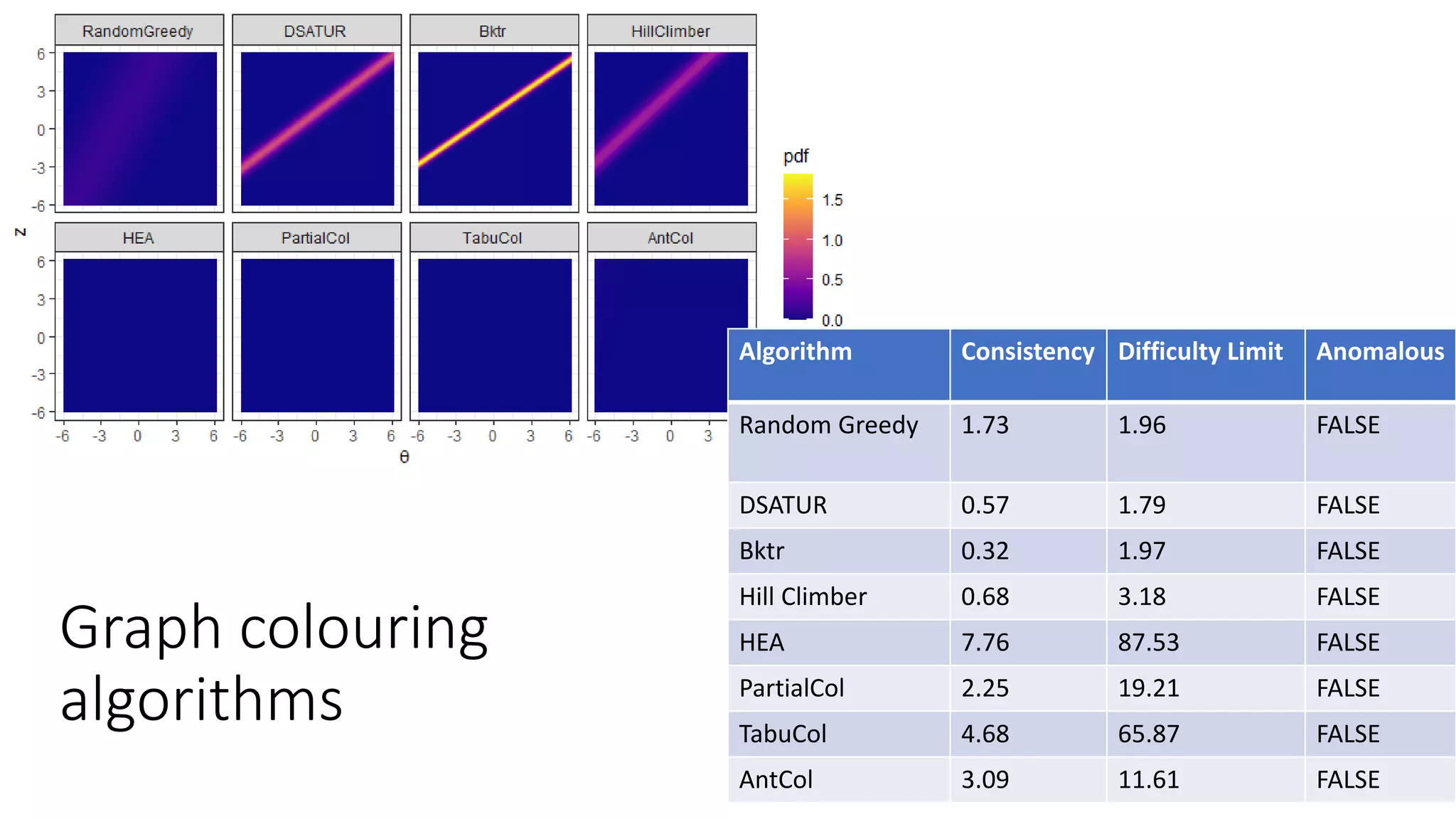
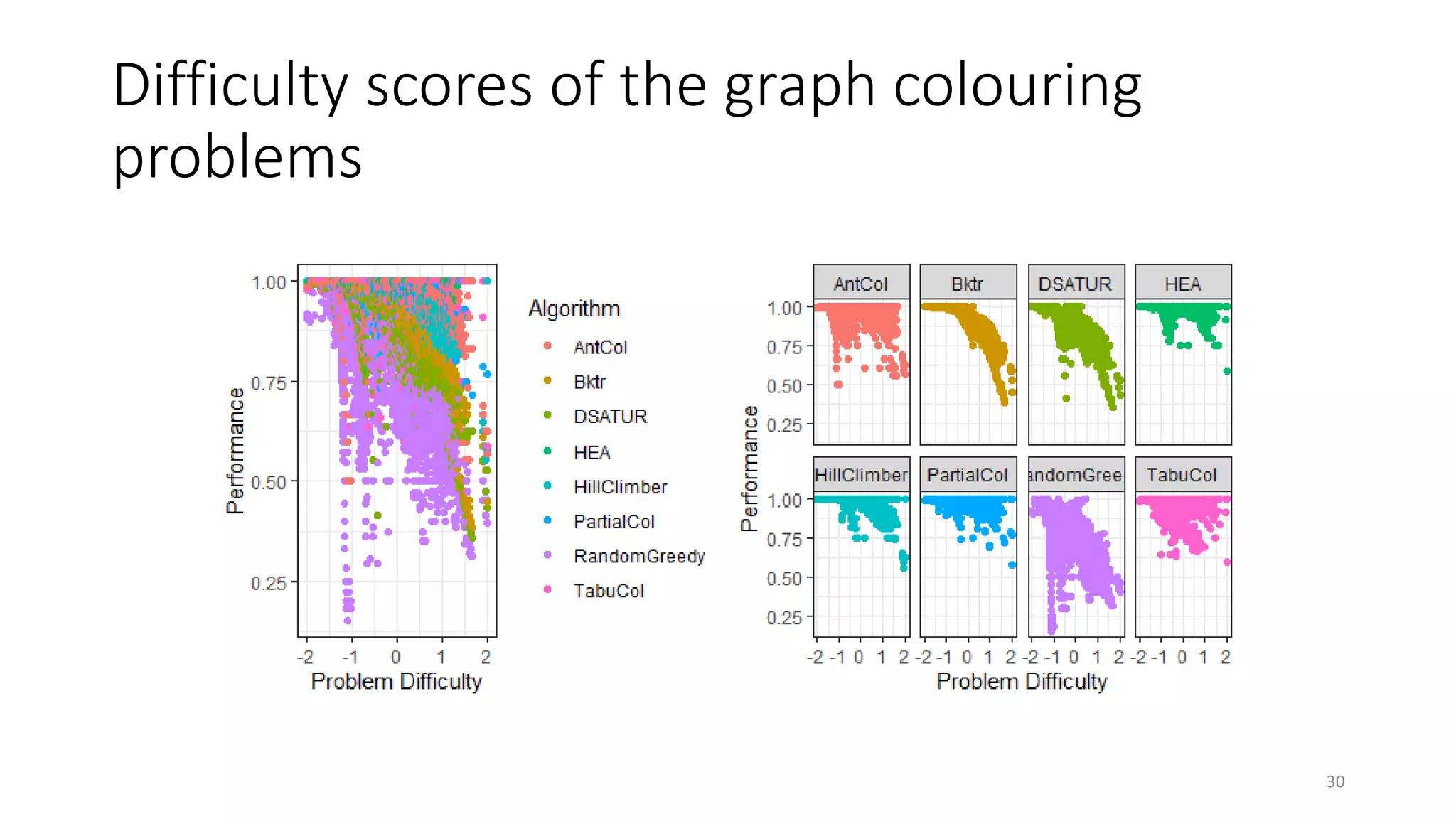
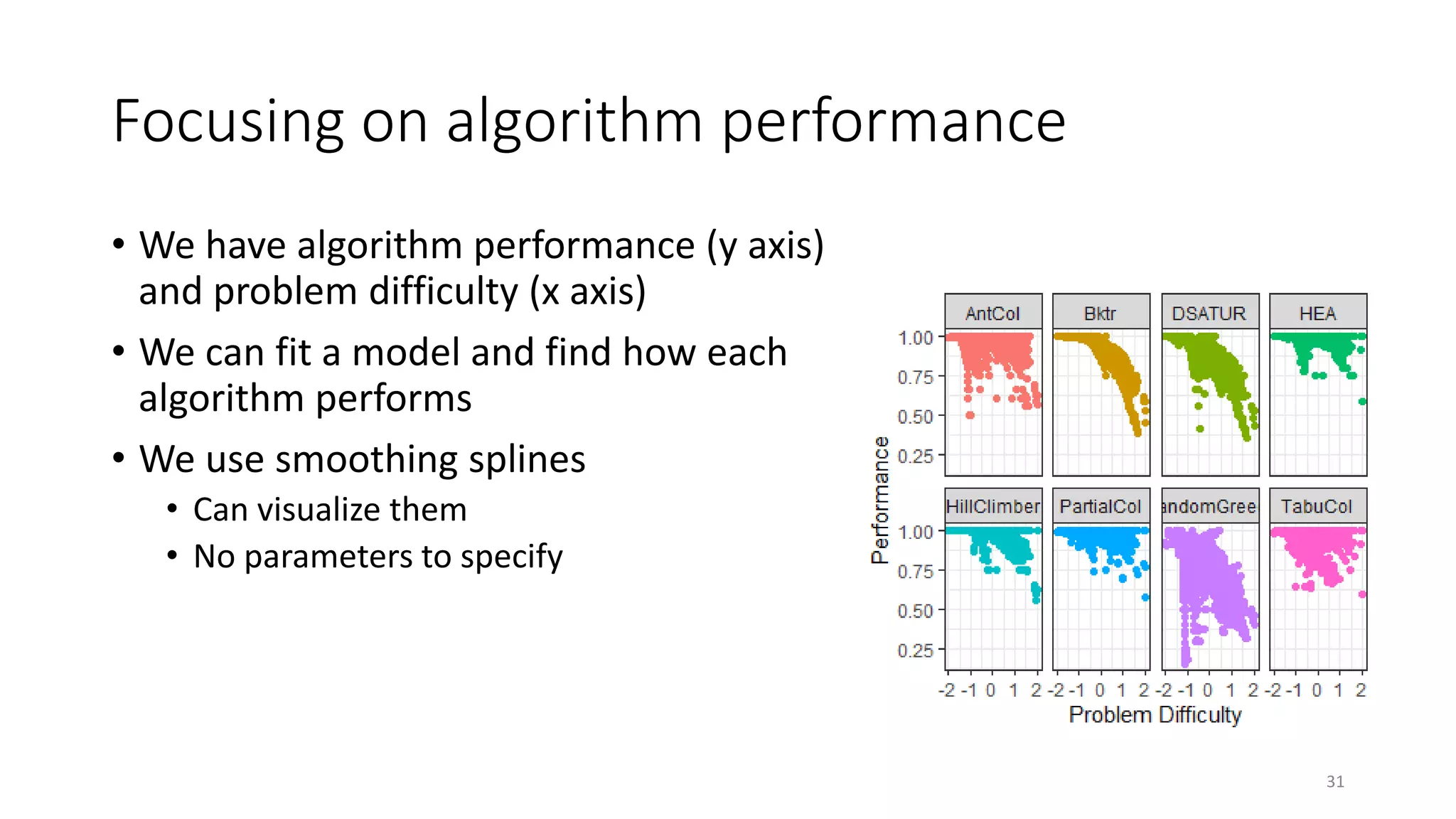
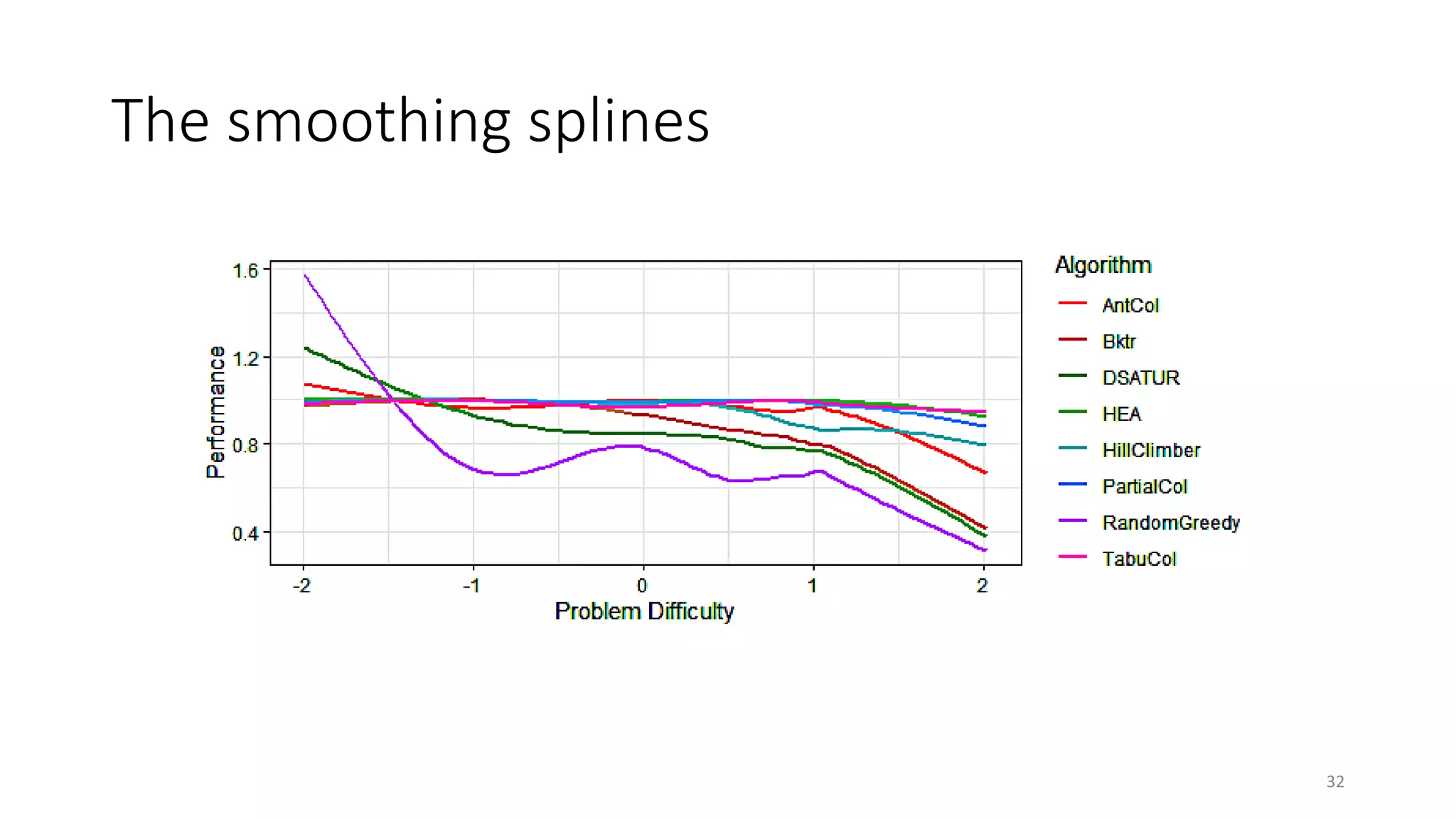
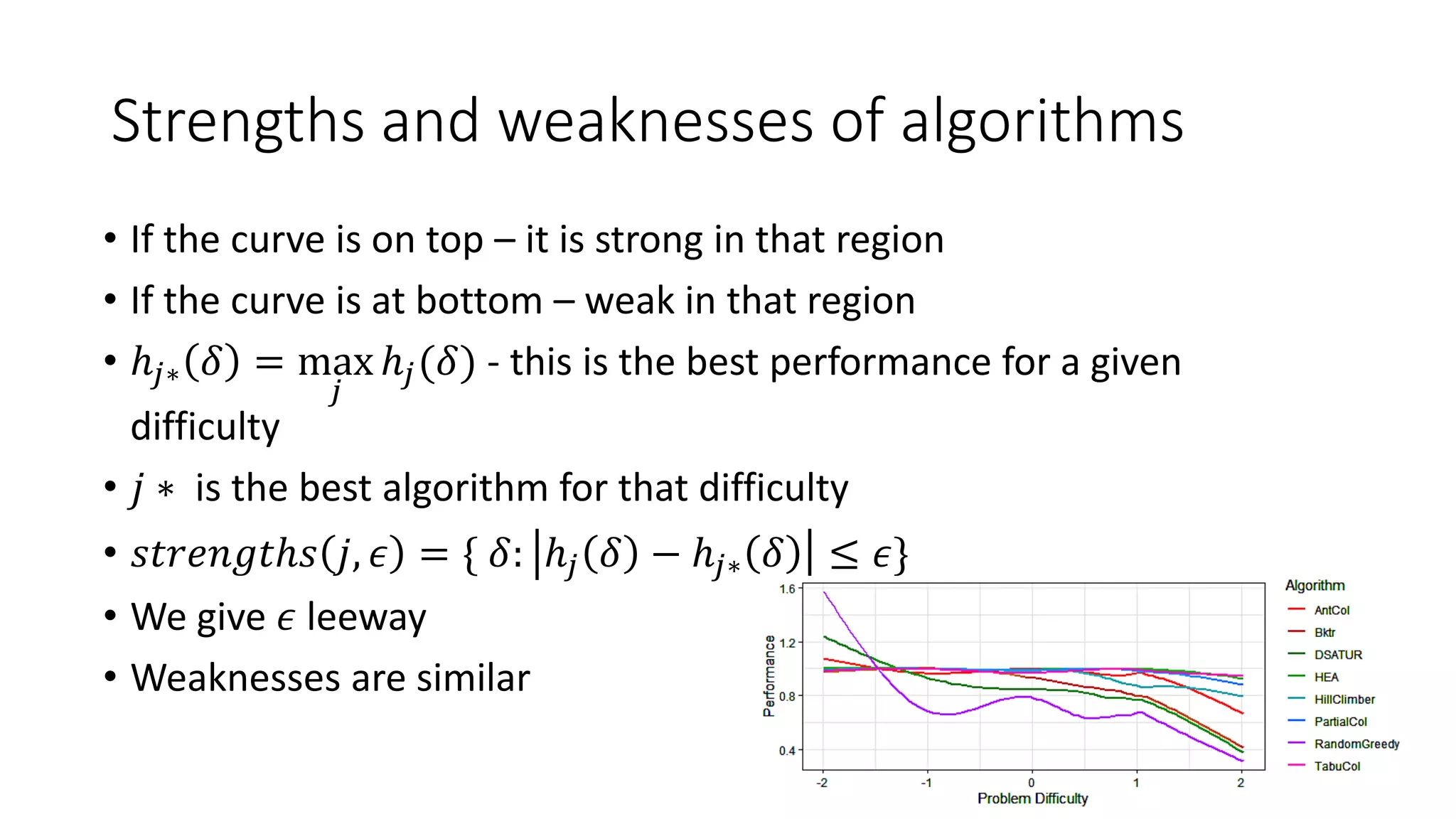
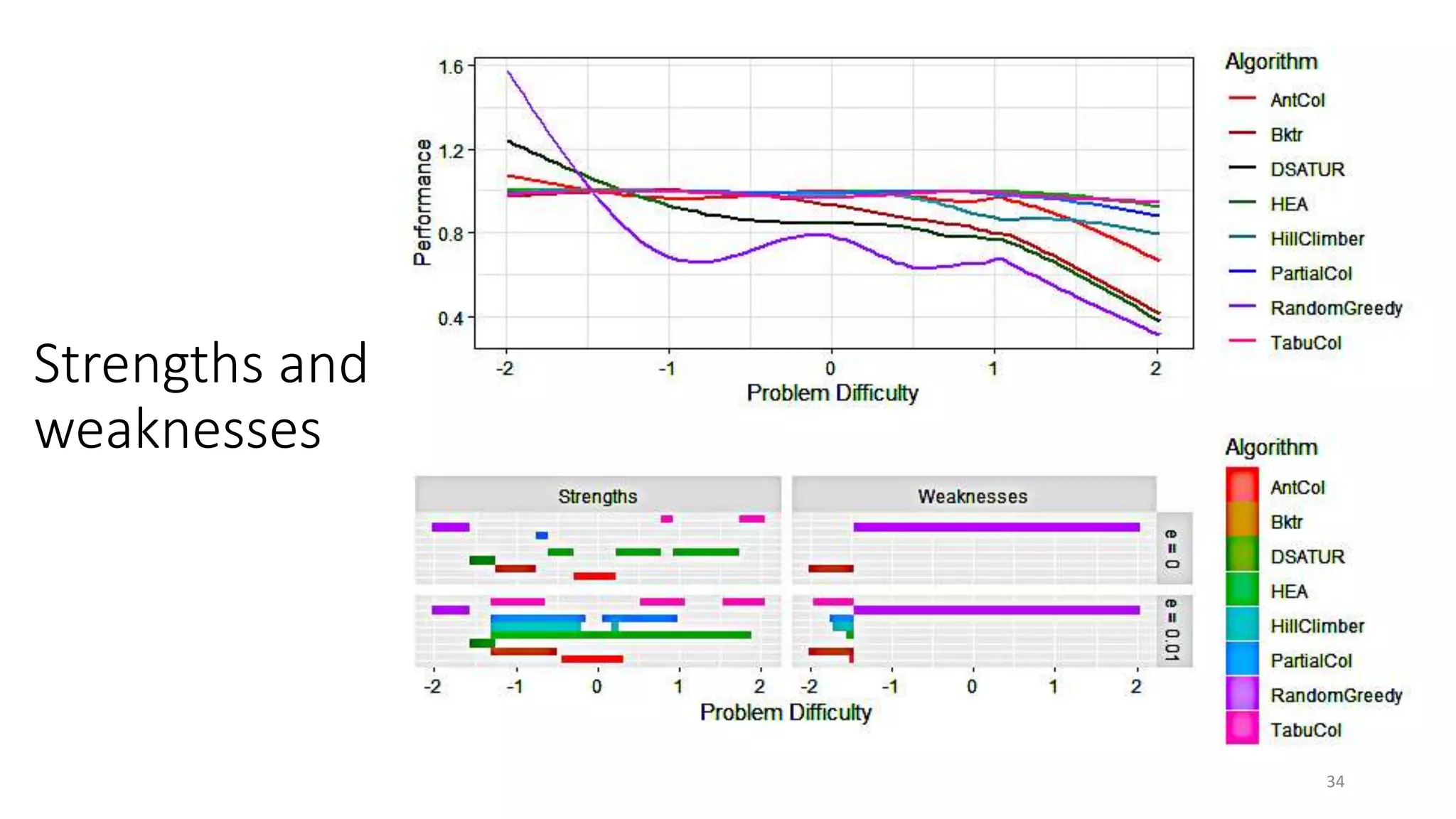
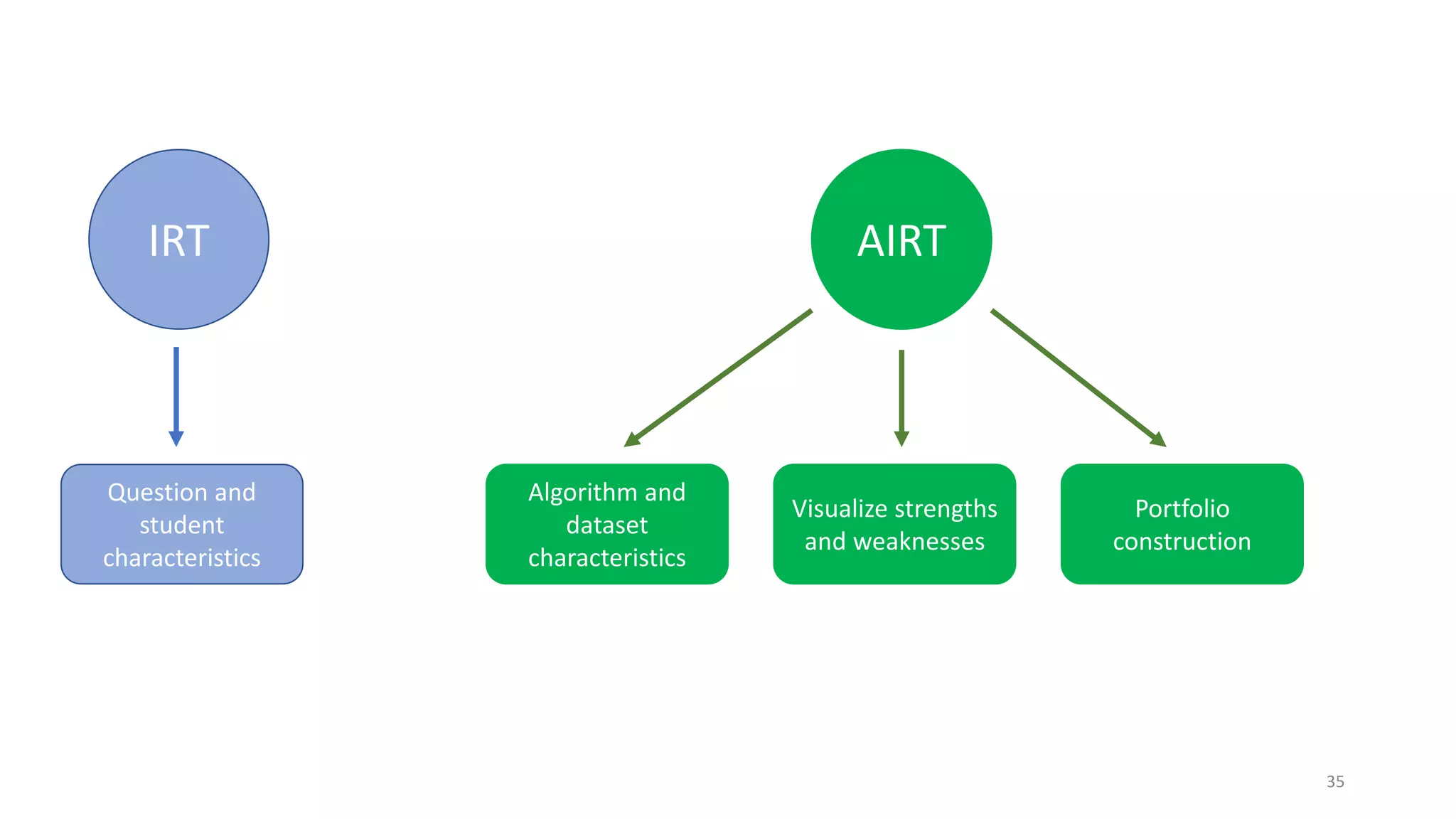
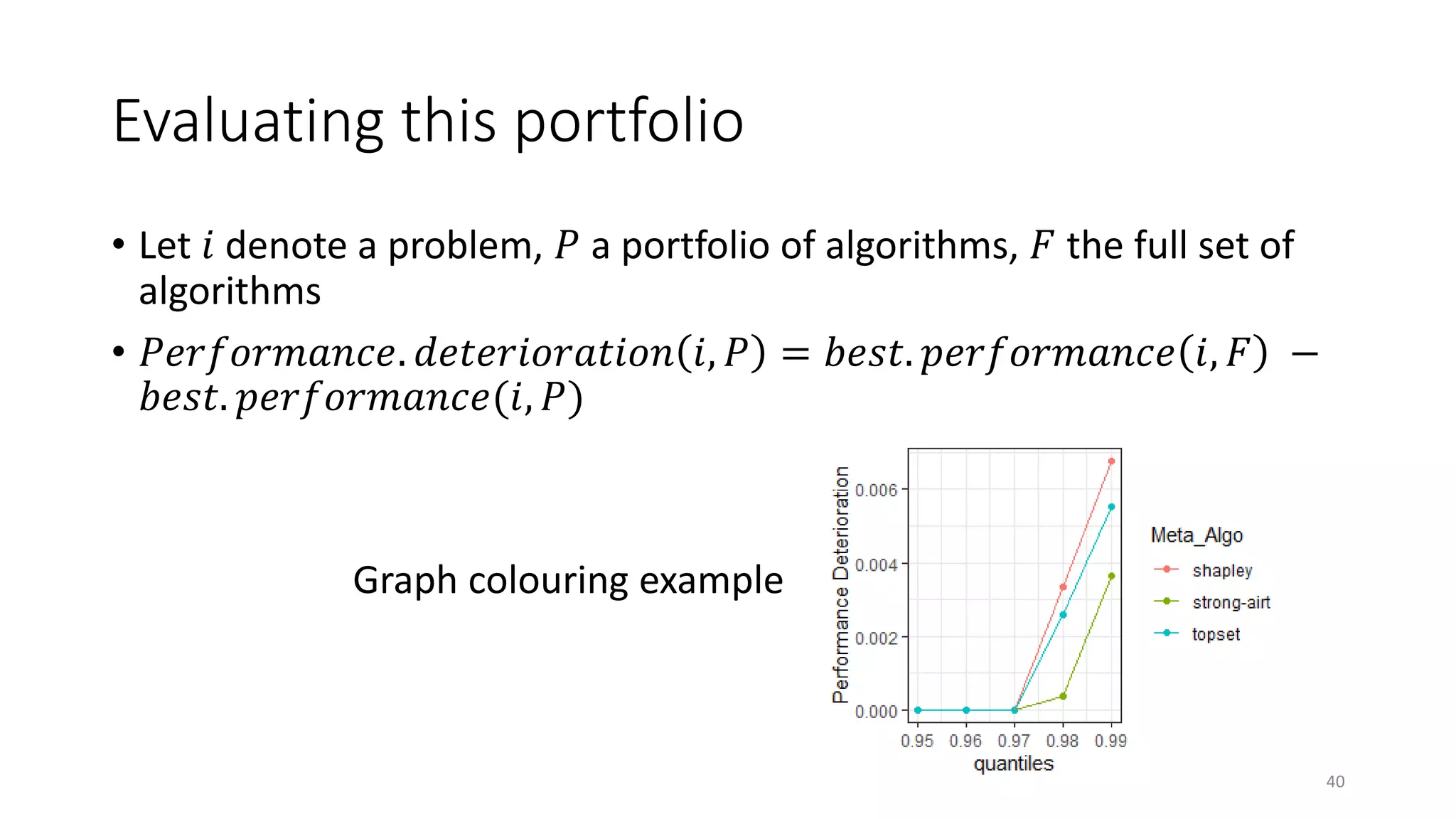
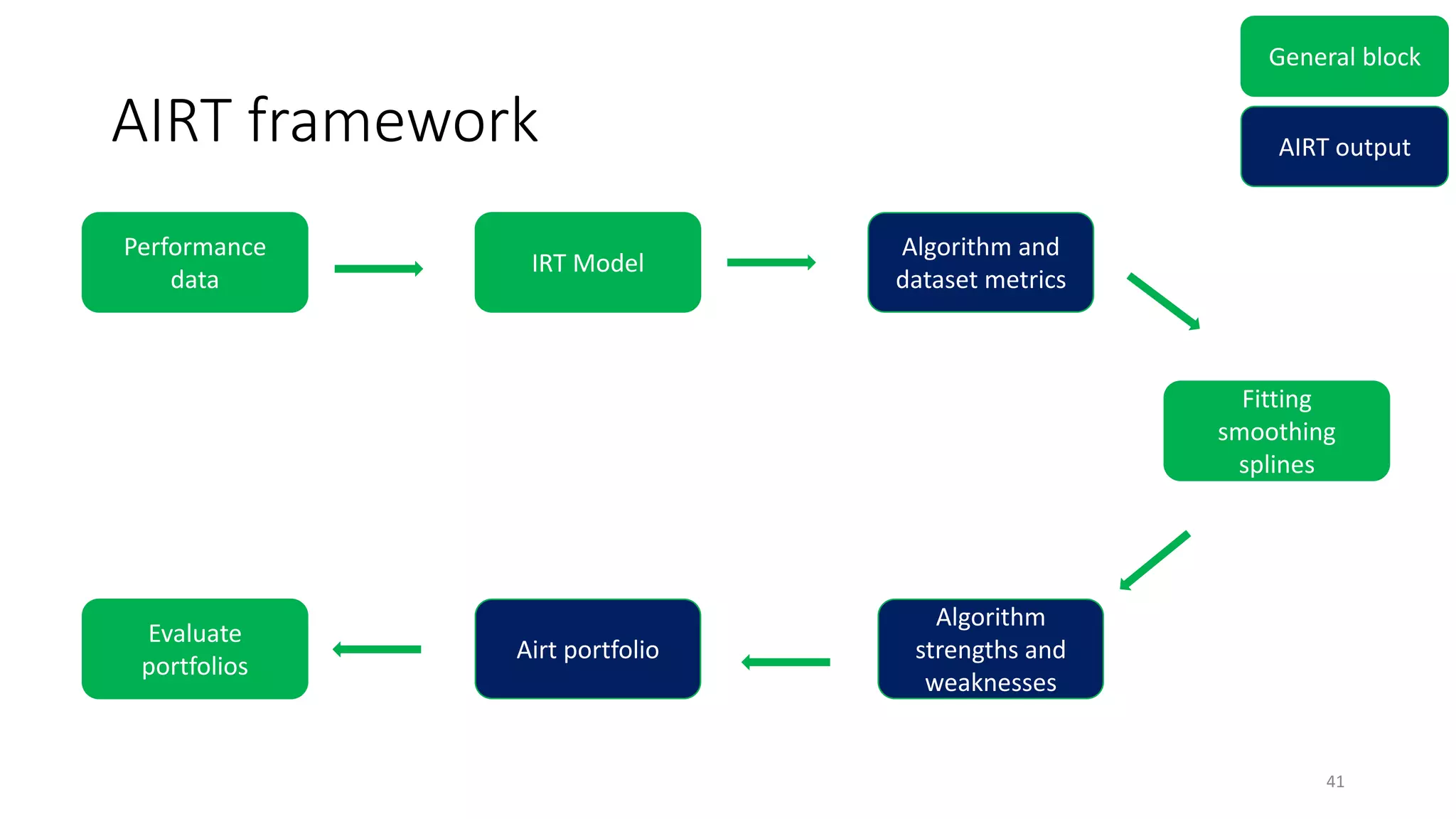
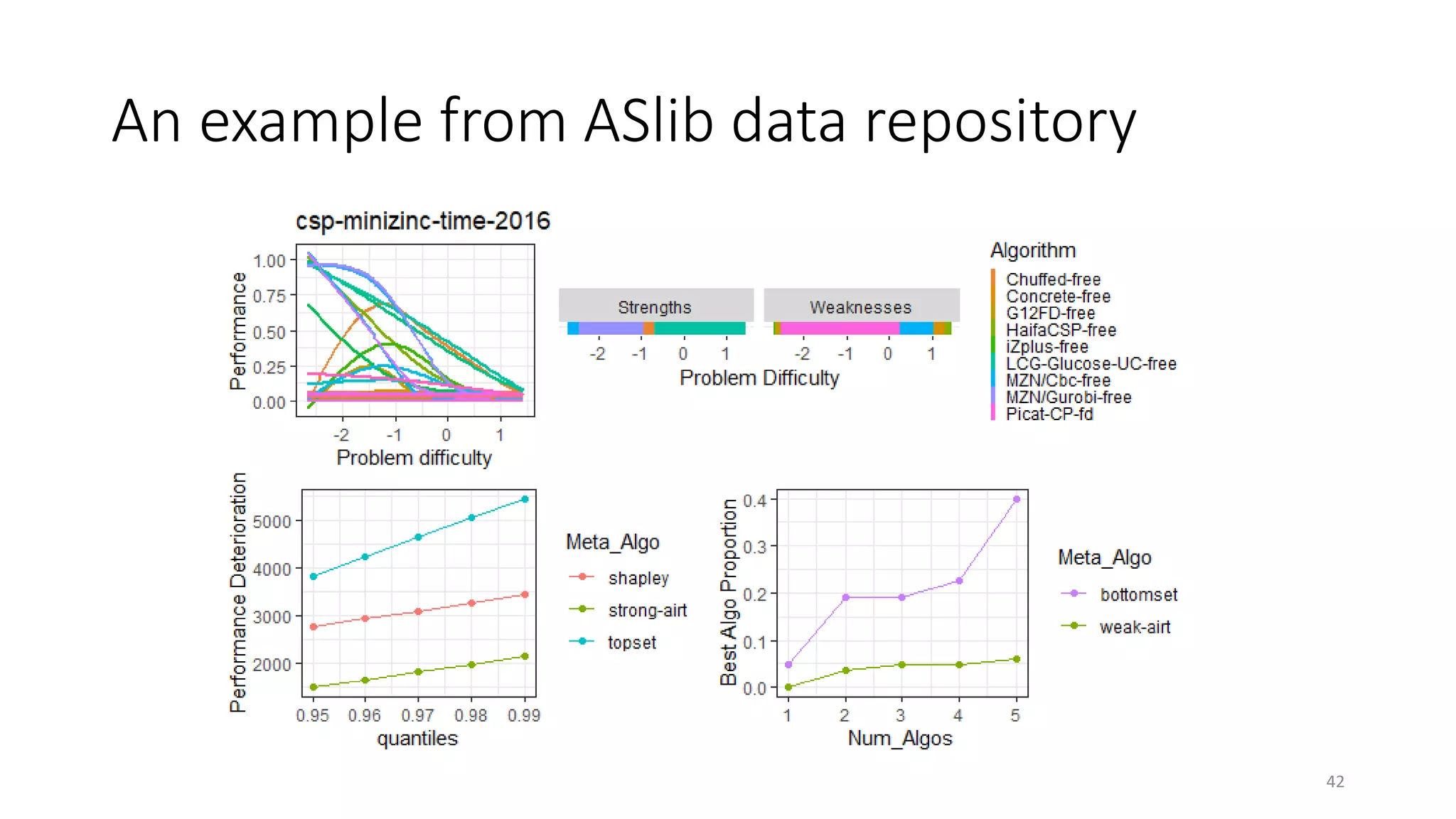
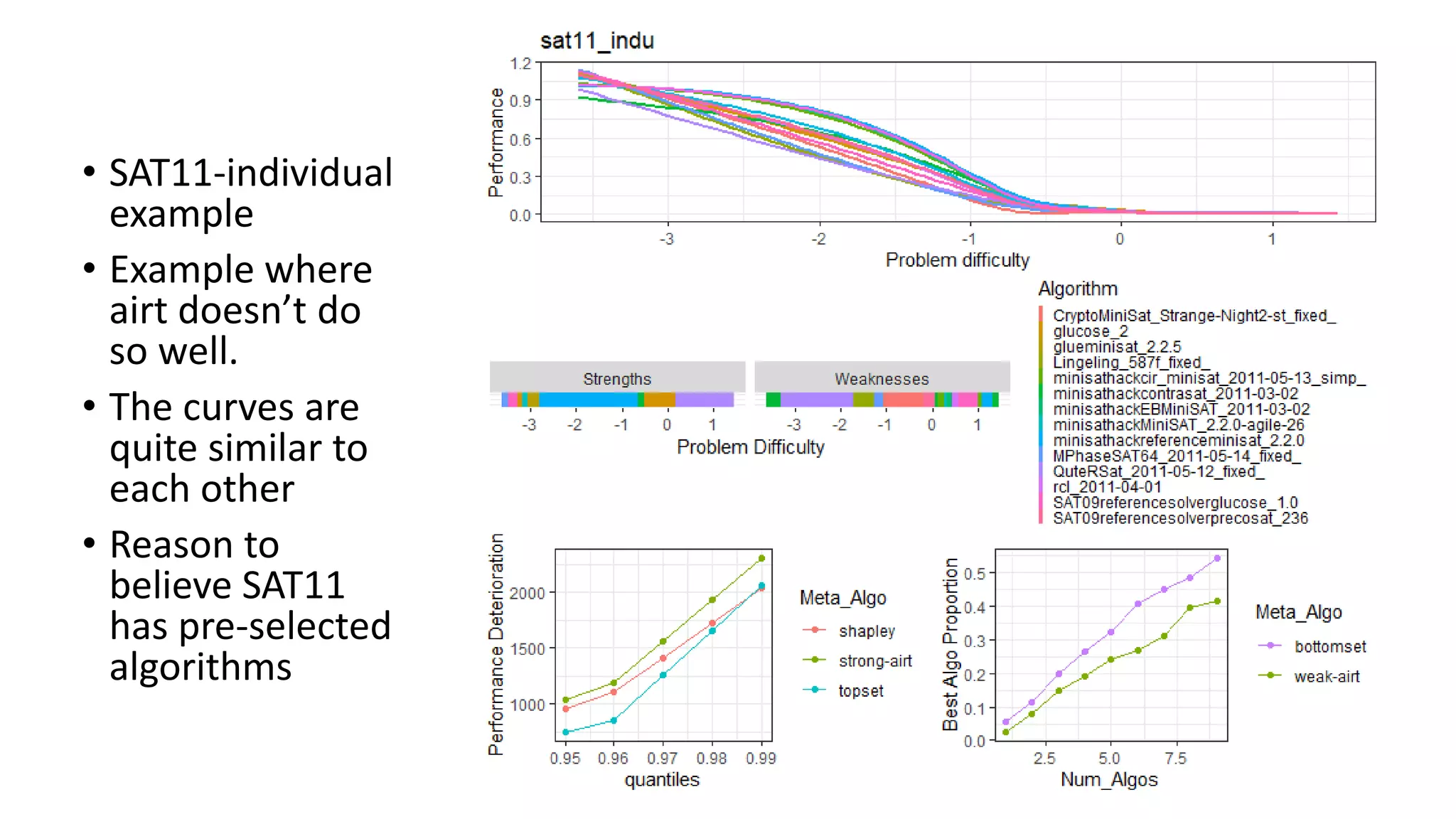
The document discusses the integration of educational models, specifically Item Response Theory (IRT), into the evaluation of algorithms within the field of explainable artificial intelligence (XAI). It outlines how IRT can help in assessing algorithm performance by measuring their anomalies, consistency, and difficulty limits, providing a clearer understanding of their strengths and weaknesses. Finally, it presents the 'airt' framework for selecting diverse algorithm portfolios that effectively address various datasets and problems.

1. Using educational
models to explain
algorithm
evaluation
Sevvandi Kandanaarachchi
Work with Kate Smith-Miles
1

2. What is an explanation?
• “To explain an event is to provide some information about its
causal history.” – Lewis , 1986 (Causal Explanation)
• “A statement or an account that makes something clear” –
Google
• “It is important to note that the solution to explainable AI is not
just ‘more AI’ “ - Miller, 2019
2

3. Explanation in the social sciences
• Miller (2019) argues for Social Science + Computer Science in XAI
“In the fields of philosophy, cognitive psychology/science, and social
psychology, there is a vast and mature body of work that studies these
exact topics. For millennia, philosophers have asked the questions
about what constitutes an explanation, what is the function of
explanations, and what are their structure. For over 50 years, cognitive
and social psychologists have analysed how people attribute and
evaluate the social behaviour of others in physical environments. For
over two decades, cognitive psychologists and scientists have
investigated how people generate explanations and how they evaluate
their quality.
I argue here that there is considerable scope to infuse this valuable
body of research into explainable AI.”
3

4. Message: Bring in the social
scientists to the party!
4

5. What is algorithm evaluation?
• Performance of many algorithms to many problems
• How do you explain the algorithm performance?
• Standard statistical analysis misses many things
5
Algo 1 Algo 2 Algo 3 Algo 4
Problem 1
Problem 2
Problem 3
Problem 4
Problem 5

6. We want to evaluate algorithms
performance in a way that we
understand algorithms and problems
better!
6

7. 7
Item Response
Theory

8. Item Response Theory
(IRT)
• Models used in social
sciences/psychometrics
• Unobservable characteristics and observed
outcomes
• Verbal or mathematical ability
• Racial prejudice or stress proneness
• Political inclinations
• Intrinsic “quality” that cannot be
measured directly
This Photo by Unknown Author is licensed under CC BY-SA

9. IRT in education
• Finds the discrimination and difficulty of test
questions
• And the ability of the test participants
• By fitting an IRT model
• In education – questions that can discriminate
between students with different ability is
preferred to “very difficult” questions.
9

10. How it works
10
Questions
Students Q 1 Q 2 Q 3 Q 4
Stu 1 0.95 0.87 0.67 0.84
Stu 2 0.57 0.49 0.78 0.77
Stu n 0.75 0.86 0.57 0.45
IRT Model
Discrimination of
questions 𝛼𝑗
Difficulty of questions 𝛽𝑗
Ability of students 𝜃𝑖 (latent trait)
Matrix 𝑌𝑁×𝑛

11. What does IRT give us?
• Q1 - discrimination 𝛼1,difficulty 𝛽1
• Q2 - discrimination 𝛼2 ,difficulty 𝛽2
• Q3 - discrimination 𝛼3 ,difficulty 𝛽3
• Q4 - discrimination 𝛼4 ,difficulty 𝛽4
• Student 1 ability 𝜃1
︙
• Student n ability 𝜃𝑛
11
Q 1 Q 2 Q 3 Q 4
Stu 1 0.95 0.87 0.67 0.84
Stu 2 0.57 0.49 0.78 0.77
Stu n 0.75 0.86 0.57 0.45

12. The causal understanding
12
𝛼𝑗 𝛽𝑗 𝜃𝑖
𝑥𝑖𝑗
Discrimination of Q j Difficulty of Q j Ability of student i
Marks of student i for Question j
Student
Question
Marks

13. IRT in Data Science/Machine Learning
• Relatively new area of research
• Seminal paper
• 2019 - Item response theory in AI: Analysing machine learning
classifiers at the instance level – F. Martínez-Plumed et al.
13

14. Dichotomous IRT
• Multiple choice
• True or false
• 𝜙 𝑥𝑖𝑗 = 1 𝜃𝑖, 𝛼𝑗, 𝑑𝑗, 𝛾𝑗 = 𝛾𝑗 +
1 −𝛾𝑗
1+exp(−𝛼𝑗(𝜃𝑖−𝑑𝑗))
• 𝑥𝑖𝑗 - outcome/score of examinee 𝑖 for item 𝑗
• 𝜃𝑖 - examinee’s (𝑖) ability
• 𝛾𝑗 - guessing parameter for item 𝑗
• 𝑑𝑗 - difficulty parameter
• 𝛼𝑗 - discrimination
This Photo by Unknown Author is licensed under CC BY-NC
14

15. Continuous IRT
• Grades out of 100
• A 2D surface of probabilities
• 𝑃(𝑥𝑖𝑗|𝜃𝑖, 𝑑𝑗, 𝛼𝑗)
15
𝑃(𝑥𝑖𝑗|𝜃𝑖, 𝑑𝑗, 𝛼𝑗)

16. Continuous IRT
• 𝑃(𝑥𝑖𝑗|𝜃𝑖, 𝑑𝑗, 𝛼𝑗)
• At a fixed 𝜃
16
𝑃(𝑥𝑖𝑗|𝜃𝑖, 𝑑𝑗, 𝛼𝑗)
𝜃 = 2
𝜃 = −3,
x axis is the normalized score

17. Mapping algorithm evaluation to IRT
IRT Model
Students
Test questions
17
Problems/datasets
Algorithms

18. New Mapping
IRT Model
Algorithms
Datasets/Problems
18

19. The new mapping
19
𝛼𝑗 𝛽𝑗 𝜃𝑖
𝑥𝑖𝑗
Discrimination of Algo j Difficulty of Algo j Ability of Dataset i
Marks of dataset i for algorithm j
Dataset
Algorithm
Performance

20. What happens to the IRT parameters?
• IRT - 𝜃𝑖 - ability of student 𝑖
• As 𝜃 increases probability of a
higher score increases
• What is 𝜃𝑖, in terms of a
dataset?
• 𝜃𝑖 easiness of the dataset
• 𝛿𝑖 = −𝜃𝑖
• 𝛿𝑖 Dataset difficulty score
20

21. Discrimination parameter
• Discrimination of item 𝑗 = 𝛼𝑗
• 𝛼𝑗increases → slope of curve
increases
• What is 𝛼𝑗, in terms of an
algorithm?
• 𝛼𝑗- lack of stability/robustness
of algo
• (1/|𝛼𝑗|) Consistency of algo
21

22. Consistent algorithms
• Education – such a question
doesn’t give any information
• Algorithms – these algorithms
are really stable or consistent
• Consistency = 1/|𝛼𝑗|
22

23. Anomalous algorithms
• Algorithms that perform poorly
on easy datasets and well on
difficult datasets
• Negative discrimination
• In education – such items are
discarded or revised
• If an algorithm anomalous, it is
interesting
• Anomalousness = sign(𝛼𝑗)
This Photo by Unknown Author is licensed under CC BY-NC-ND
23

24. Fitting the IRT model
• Maximising the expectation
• 𝐸 = 𝑁 𝑗(ln 𝛼𝑗 + ln |𝛾𝑗|) − 1/ 2 𝑖 𝑗 𝛼𝑗
2
𝛽𝑗 + 𝛾𝑗𝑧𝑖𝑗 − 𝜇𝑖
𝑡
2
+

25. After fitting the model, we get . . .
• Algorithm metrics
• Consistency, difficulty limit, anomalousness indicator
• Dataset metrics
• Difficulty scores
25

26. What can we say . . .
• Consistent algorithms give similar performance for easy or hard
datasets
• Algorithms with higher difficulty limits can handle harder problems
• Anomalous algorithms give bad performance for easy problems and
good performance for difficult problems
26

27. Example – fitting IRT model
• Graph Colouring algorithms (Smith-Miles et al 2014)
• 8 graph colouring algorithms
• RandomGreedy, DSATUR, Bktr, HillClimber, HEA, PartialCol, TabuCol, AntCol
• How many colours did each algorithm use to colour 6712 graphs
27

28. Graph colouring
algorithms
28
Algorithm Consistency Difficulty Limit Anomalous
Random Greedy 1.73 1.96 FALSE
DSATUR 0.57 1.79 FALSE
Bktr 0.32 1.97 FALSE
Hill Climber 0.68 3.18 FALSE
HEA 7.76 87.53 FALSE
PartialCol 2.25 19.21 FALSE
TabuCol 4.68 65.87 FALSE
AntCol 3.09 11.61 FALSE

29. Dataset difficulty spectrum
29

30. Difficulty scores of the graph colouring
problems
30

31. Focusing on algorithm performance
• We have algorithm performance (y axis)
and problem difficulty (x axis)
• We can fit a model and find how each
algorithm performs
• We use smoothing splines
• Can visualize them
• No parameters to specify
31

32. The smoothing splines
32

33. Strengths and weaknesses of algorithms
• If the curve is on top – it is strong in that region
• If the curve is at bottom – weak in that region
• ℎ𝑗∗ 𝛿 = max
𝑗
ℎ𝑗(𝛿) - this is the best performance for a given
difficulty
• 𝑗 ∗ is the best algorithm for that difficulty
• 𝑠𝑡𝑟𝑒𝑛𝑔𝑡ℎ𝑠 𝑗, 𝜖 = { 𝛿: ℎ𝑗 𝛿 − ℎ𝑗∗ 𝛿 ≤ 𝜖}
• We give 𝜖 leeway
• Weaknesses are similar
33

34. Strengths and
weaknesses
34

35. 35
AIRT
IRT
Question and
student
characteristics
Algorithm and
dataset
characteristics
Visualize strengths
and weaknesses
Portfolio
construction

36. AIRT performs well, when . . .
• The set of algorithms is diverse.
• Ties back to IRT basics
• IRT in education – If all the questions are equally discriminative and
difficult, IRT doesn’t add much
• IRT useful when we have a diverse set of questions and we want to
know
• Which questions are more discriminative
• Which questions are difficult
36

37. Summary
• Understand more about algorithms
• Anomalousness, consistency, difficulty limit
• Visualise the strengths and weaknesses of algorithms
• Select a portfolio of good algorithms
• Includes diagnostics
• R package airt (on CRAN)
• https://sevvandi.github.io/airt/
• Pre-print: http://bit.ly/algorithmirt
• Comprehensive Algorithm Portfolio Evaluation using Item Response Theory
• More applications included
37

38. 38

39. Algorithm portfolio selection
• Can use algorithm strengths to select a good portfolio of algorithms
• We call this portfolio airt portfolio
• airt – Algorithm IRT (old Scottish word – to guide)
• 𝑎𝑖𝑟𝑡 𝑝𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 𝜖 = 𝑠𝑒𝑡 𝑜𝑓 𝑎𝑙𝑔𝑜𝑟𝑖𝑡ℎ𝑚𝑠 𝑤𝑖𝑡ℎ 𝑠𝑡𝑟𝑒𝑛𝑔𝑡ℎ𝑠 (𝜖)
39

40. Evaluating this portfolio
• Let 𝑖 denote a problem, 𝑃 a portfolio of algorithms, 𝐹 the full set of
algorithms
• 𝑃𝑒𝑟𝑓𝑜𝑟𝑚𝑎𝑛𝑐𝑒. 𝑑𝑒𝑡𝑒𝑟𝑖𝑜𝑟𝑎𝑡𝑖𝑜𝑛 𝑖, 𝑃 = 𝑏𝑒𝑠𝑡. 𝑝𝑒𝑟𝑓𝑜𝑟𝑚𝑎𝑛𝑐𝑒 𝑖, 𝐹 −
𝑏𝑒𝑠𝑡. 𝑝𝑒𝑟𝑓𝑜𝑟𝑚𝑎𝑛𝑐𝑒(𝑖, 𝑃)
Graph colouring example
40

41. AIRT framework
41
Performance
data
IRT Model
Algorithm and
dataset metrics
Fitting
smoothing
splines
Algorithm
strengths and
weaknesses
Airt portfolio
Evaluate
portfolios
General block
AIRT output

42. An example from ASlib data repository
42

43. • SAT11-individual
example
• Example where
airt doesn’t do
so well.
• The curves are
quite similar to
each other
• Reason to
believe SAT11
has pre-selected
algorithms
43