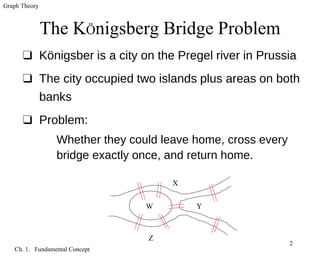
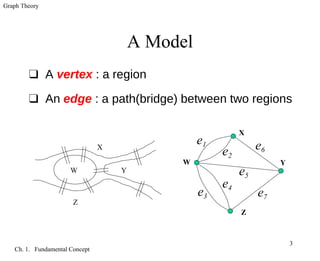
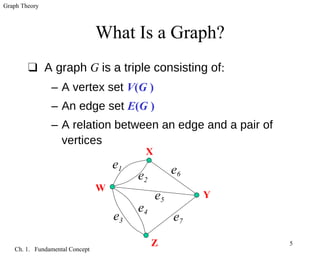
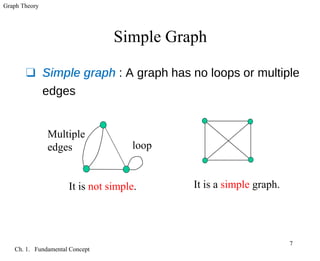
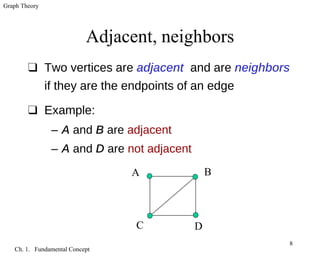
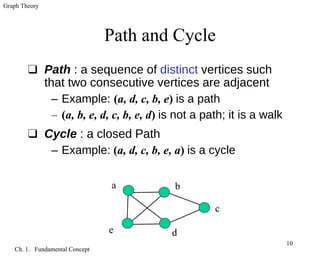
The document introduces fundamental concepts in graph theory. It discusses graphs as models to represent relationships between objects using vertices and edges. A graph is defined as a triple consisting of a vertex set, edge set, and relation between edges and vertex pairs. Different graph types are introduced, including simple graphs, loops, multiple edges, paths, cycles, and complete graphs. Adjacency, incidence, and vertex degree are also defined.

1. Graph Theory
Ch. 1. Fundamental Concept
1
Chapter 1
Fundamental Concept
1.1 What Is a Graph?
1.2 Paths, Cycles, and Trails
1.3 Vertex Degree and Counting
1.4 Directed Graphs

2. Graph Theory
Ch. 1. Fundamental Concept
2
The KÖnigsberg Bridge Problem
❑ Königsber is a city on the Pregel river in Prussia
❑ The city occupied two islands plus areas on both
banks
❑ Problem:
Whether they could leave home, cross every
bridge exactly once, and return home.
X
Y
Z
W

3. Graph Theory
Ch. 1. Fundamental Concept
3
A Model
❑ A vertex : a region
❑ An edge : a path(bridge) between two regions
e1
e2
e3
e4
e6
e5
e7
Z
Y
X
W
X
Y
Z
W

4. Graph Theory
Ch. 1. Fundamental Concept
4
General Model
❑ A vertex : an object
❑ An edge : a relation between two objects
common
member
Committee 1 Committee 2

5. Graph Theory
Ch. 1. Fundamental Concept
5
What Is a Graph?
❑ A graph G is a triple consisting of:
– A vertex set V(G )
– An edge set E(G )
– A relation between an edge and a pair of
vertices
e1
e2
e3
e4
e6
e5
e7
Z
Y
X
W

6. Graph Theory
Ch. 1. Fundamental Concept
6
Loop, Multiple edges
❑ Loop : An edge whose endpoints are equal
❑ Multiple edges : Edges have the same pair of
endpoints
loop
Multiple
edges

7. Graph Theory
Ch. 1. Fundamental Concept
7
Simple Graph
❑ Simple graph : A graph has no loops or multiple
edges
loop
Multiple
edges
It is not simple. It is a simple graph.

8. Graph Theory
Ch. 1. Fundamental Concept
8
Adjacent, neighbors
❑ Two vertices are adjacent and are neighbors
if they are the endpoints of an edge
❑ Example:
– A and B are adjacent
– A and D are not adjacent
A B
C D

9. Graph Theory
Ch. 1. Fundamental Concept
9
Finite Graph, Null Graph
❑ Finite graph : an graph whose vertex set and
edge set are finite
❑ Null graph : the graph whose vertex set and
edges are empty

10. Graph Theory
Ch. 1. Fundamental Concept
10
Path and Cycle
❑ Path : a sequence of distinct vertices such
that two consecutive vertices are adjacent
– Example: (a, d, c, b, e) is a path
– (a, b, e, d, c, b, e, d) is not a path; it is a walk
❑ Cycle : a closed Path
– Example: (a, d, c, b, e, a) is a cycle
a b
c
d
e

11. Graph Theory
Ch. 1. Fundamental Concept
11
Adjacency, Incidence, and Degree
❑ Assume ei is an edge whose endpoints are
(vj,vk)
❑ The vertices vj and vk are said to be adjacent
❑ The edge ei is said to be incident upon vj
❑ Degree of a vertex vk is the number of edges
incident upon vk . It is denoted as d(vk)
ei
vj
vk

12. Graph Theory
Ch. 1. Fundamental Concept
12
Adjacency matrix
❑ Let G = (V, E), |V| = n and |E|=m
❑ The adjacency matrix of G written A(G), is
the n-by-n matrix in which entry ai,j is the
number of edges in G with endpoints {vi, vj}.
a
b
c
d
e
w
x
y z
w x y z
0 1 1 0
1 0 2 0
1 2 0 1
0 0 1 0
w
x
y
z

13. Graph Theory
Ch. 1. Fundamental Concept
13
Complete Graph
❑ Complete Graph : a simple graph whose
vertices are pairwise adjacent
Complete Graph