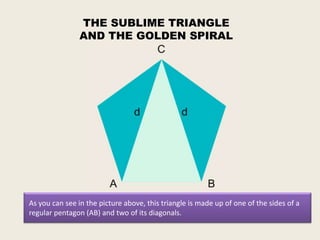
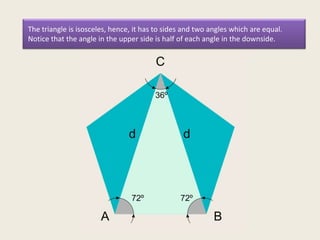
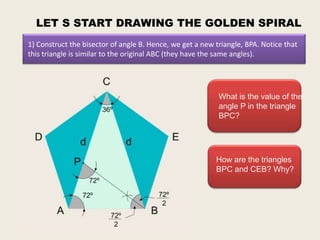
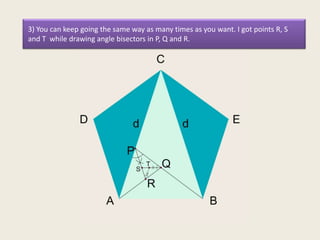
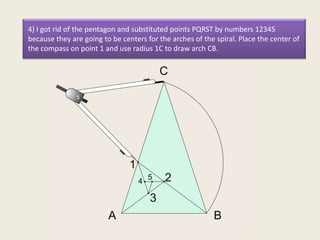
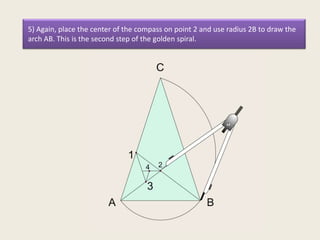
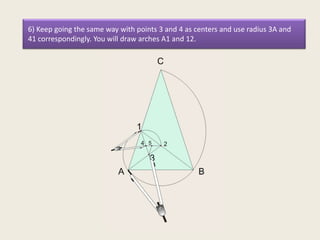
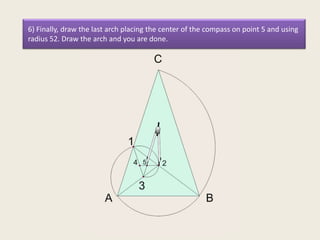
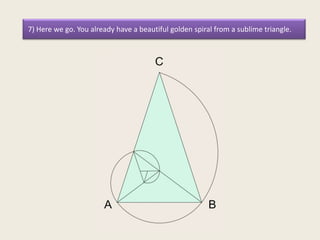
This presentation discusses the construction of the golden spiral from the sublime triangle. It begins by introducing the sublime triangle, which is made up of sides from a regular pentagon. It then demonstrates how to construct the golden spiral by repeatedly drawing angle bisectors to generate similar, smaller triangles and using the points to lay out concentric arcs that form the spiral shape. The presentation provides step-by-step instructions on drawing the angle bisectors, finding the points, and using the points and radii to construct the golden spiral arcs.

1. This presentation has been made for you by
FRANCISCO GUIJARRO BELDA
From Isaac Albéniz Secondary School
Leganés. Madrid. Spain.

2. THE SUBLIME TRIANGLE
AND THE GOLDEN SPIRAL
As you can see in the picture above, this triangle is made up of one of the sides of a
regular pentagon (AB) and two of its diagonals.

3. The triangle is isosceles, hence, it has to sides and two angles which are equal.
Notice that the angle in the upper side is half of each angle in the downside.

4. LET S START DRAWING THE GOLDEN SPIRAL
1) Construct the bisector of angle B. Hence, we get a new triangle, BPA. Notice that
this triangle is similar to the original ABC (they have the same angles).
What is the value of the
angle P in the triangle
BPC?
How are the triangles
BPC and CEB? Why?

5. 2) Again, we keep drawing an angle bisector in angle A. As a consequence, we will
get point Q and, therefore, a new triangle APQ similar to BPA and ABC. As you can
tell, we are building a decreasing series of similar triangles.

6. 3) You can keep going the same way as many times as you want. I got points R, S
and T while drawing angle bisectors in P, Q and R.

7. 4) I got rid of the pentagon and substituted points PQRST by numbers 12345
because they are going to be centers for the arches of the spiral. Place the center of
the compass on point 1 and use radius 1C to draw arch CB.

8. 5) Again, place the center of the compass on point 2 and use radius 2B to draw the
arch AB. This is the second step of the golden spiral.

9. 6) Keep going the same way with points 3 and 4 as centers and use radius 3A and
41 correspondingly. You will draw arches A1 and 12.

10. 6) Finally, draw the last arch placing the center of the compass on point 5 and using
radius 52. Draw the arch and you are done.

11. 7) Here we go. You already have a beautiful golden spiral from a sublime triangle.