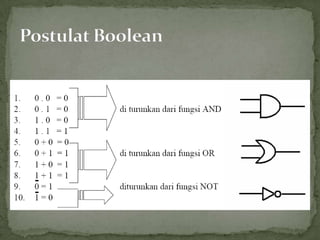
Dokumen ini membahas tentang gerbang logika dasar seperti AND, OR, dan NOT. Termasuk definisi operasi masing-masing gerbang, persamaan aljabar Boolean, dan tabel kebenaran. Juga dijelaskan teorema-teorema dasar aljabar Boolean yang digunakan untuk mengolah dan meminimumkan persamaan logika.

2.  Siswa dapat menjelaskan operasi berbagai gerbang
dasar
 Siswa dapat menjelaskan persamaan Aljabar Boole
untuk berbagai gerbang dasar
 Siswa dapat membuat Tabel Kebenaran (Truth Table)
untuk berbagai gerbang dasar

3. Gerbang logika merupakan dasar pembentukan sistem
digital. Gerbang logika beroperasi dengan bilangan
biner, sehingga disebut juga gerbang logika biner.
Tegangan yang digunakan dalam gerbang logika adalah
TINGGI (High) atau RENDAH (Low). Tegangan tinggi
berarti 1, sedangkan tegangan rendah berarti 0. gerbang
dasar logika terdiri dari:
 Gerbang AND
 Gerbang OR
 Gerbang NOT

4.  Gerbang AND didefinisikan sebagai gerbang logika
yang memberikan keadaan level logika 1 pada
outputnya, jika semua keadaan inputnya berlevel
logika 1 (tinggi).

5. A B C
0 0 0
0 1 0
1 0 0
1 1 1

7.  Gerbang OR didefinisikan sebagai gerbang logika yang
memberikan keadaan logika 1 (tinggi) pada outputnya,
jika keadaan salah satu atau lebih inputnya berlogika 1
(tinggi).

8. A B C
0 0 0
0 1 1
1 0 1
1 1 1
OrGateTabel.swf

10.  NOT merupakan gerbang logika yang memberikan
keadaan level logika 1 pada outputnya, jika keadaan
outputnya berlevel logika 0 atau sebaliknya.

11. A Y
0 1
1 0

14.  Tabel di bawah menunjukkan teorem asas Aljabar
Boolean yang akan digunakan untuk mengolah dan
meminimumkan persamaan.

15.  Dua peraturan yang pertama untuk setiap logika
menunjukkan bahawa persamaan di sebelah kiri
adalah sama dengan persamaan di sebelah kanan
walaupun tertib operasi logiknya berbeza. Manakala
persamaan ketiga menunjukkan bagaimana sesuatu
persamaan boleh dipanjangkan atau difaktorkan.

16. No AND OR KETERANGAN
1
2
3
4
5
6
7
8
9
(A.B).C = A.(B.C)
A .B = B .A
(A+B).(A+C)=A+(B.C)
A.O = O
A.A = A
A.A= O
A = A
A.O= O
A .1 = A
A.(A + B ) = A
(A+B)+C=A+(B+C)
A+B=B+A
(A.B)+(A.C)=A(B+C)
A+1= 1
A+A=A
A+ A=1
A = A
A + O = A
A + 1 = 1
A + (A.B) = A
Hk.Asosiatif
Hk.Komutatif
Hk.Distributif
Hk.Identitas
Hk.Idempoten
Hk.Inversi/Negasi
Hk.Negasi Ganda
Hk.Hubungan Dgn
Suatu Konstanta
Hk.Absorbsi

17.  Teorem ini menyatakan cara untuk memisahkan
pelengkap pada sebutan panjang, yaitu sebutan yang
mempunyai lebih dari satu pemboleh ubah. Dengan
kata lain, teorem ini menghapuskan “pelengkap
sebutan” dengan menyonsangkan setiap pemboleh
ubah dan operator dalam sebutan tersebut.

18.  Buktikan persamaan berikut menggunakan aljabar
boolean atau tabel kebenaran

19.  Gunakan persamaan boole untuk menyederhanakan
persamaan berikut