Lecture

1. ‫الرسوم‬ ‫نظرية‬ ‫في‬ ‫تطبيقات‬
‫الرسوم‬ ‫نظرية‬ ‫في‬ ‫تطبيقات‬
‫السويسري‬ ‫العالم‬ ‫إلى‬ ‫الرسوم‬ ‫لنظرية‬ ‫المعروفة‬ ‫البدايات‬ ‫ترجع‬
‫السويسري‬ ‫العالم‬ ‫إلى‬ ‫الرسوم‬ ‫لنظرية‬ ‫المعروفة‬ ‫البدايات‬ ‫ترجع‬
(
(
1707-1783
1707-1783
)
)
Leonhard Euler
Leonhard Euler
‫نظرية‬ ‫بأبو‬ ‫يلقب‬ ‫(الذي‬
‫نظرية‬ ‫بأبو‬ ‫يلقب‬ ‫(الذي‬
‫حل‬ ‫بنشر‬ ‫قام‬ ‫عندما‬ ‫وذلك‬ )‫التوبولوجي‬ ‫علم‬ ‫بأبو‬ ‫أيضا‬ ‫كما‬ ‫الرسوم‬
‫حل‬ ‫بنشر‬ ‫قام‬ ‫عندما‬ ‫وذلك‬ )‫التوبولوجي‬ ‫علم‬ ‫بأبو‬ ‫أيضا‬ ‫كما‬ ‫الرسوم‬
‫عام‬ ‫في‬ ‫السبعة‬ ‫الجسور‬ ‫مسألة‬
‫عام‬ ‫في‬ ‫السبعة‬ ‫الجسور‬ ‫مسألة‬
1736
1736
‫الرسوم‬ ‫نظرية‬ ‫ظهرت‬ .‫م‬
‫الرسوم‬ ‫نظرية‬ ‫ظهرت‬ .‫م‬
‫ما‬ ‫سرعان‬ ‫ولكن‬ ‫واأللغاز‬ ‫األلعاب‬ ‫بعض‬ ‫لحل‬ ‫كأداة‬ ‫البداية‬ ‫في‬
‫ما‬ ‫سرعان‬ ‫ولكن‬ ‫واأللغاز‬ ‫األلعاب‬ ‫بعض‬ ‫لحل‬ ‫كأداة‬ ‫البداية‬ ‫في‬
‫مثل‬ ‫العلوم‬ ‫مختلف‬ ‫في‬ ‫واسعة‬ ‫مجاالت‬ ‫تشمل‬ ‫تطبيقاتها‬ ‫أصبحت‬
‫مثل‬ ‫العلوم‬ ‫مختلف‬ ‫في‬ ‫واسعة‬ ‫مجاالت‬ ‫تشمل‬ ‫تطبيقاتها‬ ‫أصبحت‬
‫واالقتصاد‬ ‫العمليات‬ ‫وبحوث‬ ‫الكيمياء‬ ‫و‬ ‫والتخطيط‬ ‫الحاسب‬ ‫علوم‬
‫واالقتصاد‬ ‫العمليات‬ ‫وبحوث‬ ‫الكيمياء‬ ‫و‬ ‫والتخطيط‬ ‫الحاسب‬ ‫علوم‬
‫وعلم‬ ‫واالجتماع‬ ‫(اللغة‬ ‫الحياة‬ ‫علوم‬ ‫من‬ ‫وغيرها‬ ‫الكهربية‬ ‫والهندسة‬
‫وعلم‬ ‫واالجتماع‬ ‫(اللغة‬ ‫الحياة‬ ‫علوم‬ ‫من‬ ‫وغيرها‬ ‫الكهربية‬ ‫والهندسة‬
.)‫الجينات‬
.)‫الجينات‬
‫ـــــــــ‬
‫ـــــــــ‬
‫حتى‬ ‫الرياضيات‬ ‫مجال‬ ‫في‬ ‫إنتاجا‬ ‫العلماء‬ ‫أكثر‬ ‫أويلر‬ ‫العالم‬ ‫د‬ُ
‫ع‬‫ي‬ *
‫حتى‬ ‫الرياضيات‬ ‫مجال‬ ‫في‬ ‫إنتاجا‬ ‫العلماء‬ ‫أكثر‬ ‫أويلر‬ ‫العالم‬ ‫د‬ُ
‫ع‬‫ي‬ *
‫كانت‬ ‫لقد‬ .‫الرياضيات‬ ‫أفرع‬ ‫بجميع‬ ‫اسمه‬ ‫اقترن‬ ‫ولقد‬ ,‫هذا‬ ‫وقتنا‬
‫كانت‬ ‫لقد‬ .‫الرياضيات‬ ‫أفرع‬ ‫بجميع‬ ‫اسمه‬ ‫اقترن‬ ‫ولقد‬ ,‫هذا‬ ‫وقتنا‬
‫حياته‬ ‫خالل‬ ‫نشره‬ ‫ما‬ ‫حصيلة‬
‫حياته‬ ‫خالل‬ ‫نشره‬ ‫ما‬ ‫حصيلة‬
886
886
‫مماته‬ ‫بعد‬ ‫وترك‬ ً‫ا‬‫وبحث‬ ً‫ا‬‫كتاب‬
‫مماته‬ ‫بعد‬ ‫وترك‬ ً‫ا‬‫وبحث‬ ً‫ا‬‫كتاب‬
‫سانت‬ ‫ألكاديمية‬ ‫العلمية‬ ‫المجلة‬ ‫في‬ ‫نشرها‬ ‫استمر‬ ‫التي‬ ‫األبحاث‬ ‫من‬
‫سانت‬ ‫ألكاديمية‬ ‫العلمية‬ ‫المجلة‬ ‫في‬ ‫نشرها‬ ‫استمر‬ ‫التي‬ ‫األبحاث‬ ‫من‬
‫لفترة‬ ‫بتسبرج‬
‫لفترة‬ ‫بتسبرج‬
47
47
‫سنة‬
‫سنة‬

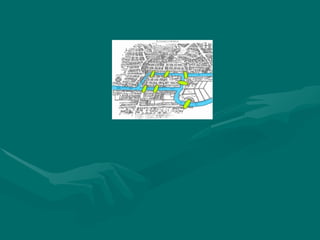
2. ‫السبعة‬ ‫الجسور‬ ‫مسالة‬
‫السبعة‬ ‫الجسور‬ ‫مسالة‬
The seven bridge of Konigsberg
The seven bridge of Konigsberg
•
‫مدينة‬ ‫في‬
‫مدينة‬ ‫في‬
Konigsberg
Konigsberg
‫يوجد‬
‫يوجد‬
7
7
‫والسؤال‬ ‫نهر‬ ‫على‬ ‫جسور‬
‫والسؤال‬ ‫نهر‬ ‫على‬ ‫جسور‬
‫كل‬ ‫على‬ ‫تعبر‬ ‫أن‬ ‫النهر‬ ‫حول‬ ‫ما‬ ‫مكان‬ ‫من‬ ‫يمكنك‬ ‫هل‬ ‫هو‬
‫كل‬ ‫على‬ ‫تعبر‬ ‫أن‬ ‫النهر‬ ‫حول‬ ‫ما‬ ‫مكان‬ ‫من‬ ‫يمكنك‬ ‫هل‬ ‫هو‬
‫نقطة‬ ‫إلى‬ ‫وترجع‬ ‫واحدة‬ ‫مرة‬ ‫السبعة‬ ‫الجسور‬ ‫من‬ ‫جسر‬
‫نقطة‬ ‫إلى‬ ‫وترجع‬ ‫واحدة‬ ‫مرة‬ ‫السبعة‬ ‫الجسور‬ ‫من‬ ‫جسر‬
‫البداية؟‬
‫البداية؟‬
•
‫إال‬ ,‫الحدوث‬ ‫مستحيل‬ ‫هذا‬ ‫أن‬ ‫تيقن‬ ‫الجميع‬ ‫أن‬ ‫من‬ ‫الرغم‬ ‫على‬
‫إال‬ ,‫الحدوث‬ ‫مستحيل‬ ‫هذا‬ ‫أن‬ ‫تيقن‬ ‫الجميع‬ ‫أن‬ ‫من‬ ‫الرغم‬ ‫على‬
‫ممكن؟‬ ‫غير‬ ‫لماذا‬ ‫هو‬ ‫ينقص‬ ‫كان‬ ‫ما‬
‫ممكن؟‬ ‫غير‬ ‫لماذا‬ ‫هو‬ ‫ينقص‬ ‫كان‬ ‫ما‬

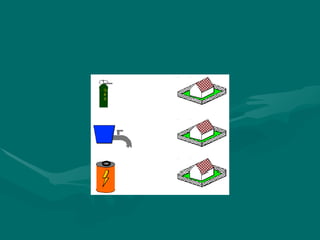
6. The utilities problem
The utilities problem
•
‫ويراد‬ )‫وغاز‬ ‫وكهرباء‬ ‫(ماء‬ ‫مصادر‬ ‫وثالث‬ ‫منازل‬ ‫ثالثة‬ ‫لدينا‬
‫ويراد‬ )‫وغاز‬ ‫وكهرباء‬ ‫(ماء‬ ‫مصادر‬ ‫وثالث‬ ‫منازل‬ ‫ثالثة‬ ‫لدينا‬
‫هل‬ ‫والسؤال‬ ‫الثالث‬ ‫المصادر‬ ‫بهذه‬ ‫المنازل‬ ‫هذه‬ ‫توصيل‬
‫هل‬ ‫والسؤال‬ ‫الثالث‬ ‫المصادر‬ ‫بهذه‬ ‫المنازل‬ ‫هذه‬ ‫توصيل‬
‫المصادر؟‬ ‫هذه‬ ‫لخطوط‬ ‫تقاطع‬ ‫بدون‬ ‫ذلك‬ ‫يتم‬ ‫أن‬ ‫ممكن‬
‫المصادر؟‬ ‫هذه‬ ‫لخطوط‬ ‫تقاطع‬ ‫بدون‬ ‫ذلك‬ ‫يتم‬ ‫أن‬ ‫ممكن‬

8. Instant Insanity
Instant Insanity
•
‫بأربعة‬ ‫ملونة‬ ‫مكعب‬ ‫لكل‬ ‫الستة‬ ‫األوجه‬, ‫مكعبات‬ ‫أربعة‬ ‫لدينا‬
‫بأربعة‬ ‫ملونة‬ ‫مكعب‬ ‫لكل‬ ‫الستة‬ ‫األوجه‬, ‫مكعبات‬ ‫أربعة‬ ‫لدينا‬
‫والمطلوب‬ ‫واحدة‬ ‫مرة‬ ‫األقل‬ ‫على‬ ‫يظهر‬ ‫لون‬ ‫كل‬ ‫بحيث‬ ‫ألوان‬
‫والمطلوب‬ ‫واحدة‬ ‫مرة‬ ‫األقل‬ ‫على‬ ‫يظهر‬ ‫لون‬ ‫كل‬ ‫بحيث‬ ‫ألوان‬
‫على‬ ‫األلوان‬ ‫جميع‬ ‫يظهر‬ ‫بحيث‬ ‫بعضها‬ ‫فوق‬ ‫المكعبات‬ ‫وضع‬
‫على‬ ‫األلوان‬ ‫جميع‬ ‫يظهر‬ ‫بحيث‬ ‫بعضها‬ ‫فوق‬ ‫المكعبات‬ ‫وضع‬
‫أوجه‬ ‫األربعة‬ ‫كل‬
‫أوجه‬ ‫األربعة‬ ‫كل‬
.
.

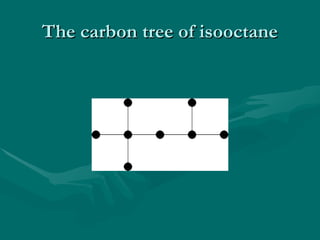
10. Enumeration of chemical molecules
Enumeration of chemical molecules
•
‫عام‬ ‫في‬
‫عام‬ ‫في‬
1870
1870
‫البريطاني‬ ‫العالم‬ ‫استخدم‬ ‫م‬
‫البريطاني‬ ‫العالم‬ ‫استخدم‬ ‫م‬
1821
1821
-
-
1895
1895
)
)
)
)
Arthur Cayley
Arthur Cayley
‫عد‬ ‫في‬ ‫الرسوم‬ ‫نظرية‬ ‫من‬ ‫األشجار‬ ‫مفهوم‬
‫عد‬ ‫في‬ ‫الرسوم‬ ‫نظرية‬ ‫من‬ ‫األشجار‬ ‫مفهوم‬
‫التركيب‬ ‫لها‬ ‫التي‬ ‫المختلفة‬ ‫الكيميائية‬ ‫المركبات‬
‫التركيب‬ ‫لها‬ ‫التي‬ ‫المختلفة‬ ‫الكيميائية‬ ‫المركبات‬
CnH2n+2
CnH2n+2
.
.
•
The carbon tree of ethane
The carbon tree of ethane
•
C
C
‫ـــــــــــــ‬
‫ـــــــــــــ‬
C
C
•
The carbon tree of ethane as a graph
The carbon tree of ethane as a graph
2
2 
n
n
H
C

12. The carbon tree of isooctane
The carbon tree of isooctane

13. The carbon tree of octane
The carbon tree of octane

14. The shortest path problem
The shortest path problem
•
‫على‬ ‫موضح‬ ‫الطرق‬ ‫ببعض‬ ‫متصلة‬ ‫لمدن‬ ‫خريطة‬ ‫لدينا‬ ‫بفرض‬
‫على‬ ‫موضح‬ ‫الطرق‬ ‫ببعض‬ ‫متصلة‬ ‫لمدن‬ ‫خريطة‬ ‫لدينا‬ ‫بفرض‬
‫طول‬ ‫هو‬ ‫ما‬ ‫السؤال‬ .)‫(مثال‬ ‫بالكيلومتر‬ ‫أطوالها‬ ‫الطرق‬ ‫هذه‬
‫طول‬ ‫هو‬ ‫ما‬ ‫السؤال‬ .)‫(مثال‬ ‫بالكيلومتر‬ ‫أطوالها‬ ‫الطرق‬ ‫هذه‬
‫ألخرى؟‬ ‫مدينة‬ ‫من‬ ‫طريق‬ ‫أقصر‬
‫ألخرى؟‬ ‫مدينة‬ ‫من‬ ‫طريق‬ ‫أقصر‬

15. The traveling salesman problem
The traveling salesman problem
•
‫مرة‬ ‫مدينة‬ ‫كل‬ ‫معينة‬ ‫مدن‬ ‫مجموعة‬ ‫يزور‬ ‫أن‬ ‫لمسافر‬ ‫كيف‬
‫مرة‬ ‫مدينة‬ ‫كل‬ ‫معينة‬ ‫مدن‬ ‫مجموعة‬ ‫يزور‬ ‫أن‬ ‫لمسافر‬ ‫كيف‬
‫ممكنة؟‬ ‫مسافة‬ ‫أقل‬ ‫في‬ ‫المدينة‬ ‫لنفس‬ ‫ويعود‬ ‫واحدة‬
‫ممكنة؟‬ ‫مسافة‬ ‫أقل‬ ‫في‬ ‫المدينة‬ ‫لنفس‬ ‫ويعود‬ ‫واحدة‬

16. •
Example
Example
•
If the distances between 5 cities A, B, C, D, and
If the distances between 5 cities A, B, C, D, and
E are given in the following figure. Find the
E are given in the following figure. Find the
shortest possible route
shortest possible route

17. The Chinese postman problem
The Chinese postman problem
•
‫إلى‬ ‫أخرى‬ ‫مرة‬ ‫ويرجع‬ ‫الخطابات‬ ‫جميع‬ ‫يوصل‬ ‫أن‬ ‫البريد‬ ‫لساعي‬ ‫كيف‬
‫إلى‬ ‫أخرى‬ ‫مرة‬ ‫ويرجع‬ ‫الخطابات‬ ‫جميع‬ ‫يوصل‬ ‫أن‬ ‫البريد‬ ‫لساعي‬ ‫كيف‬
‫؟‬ ‫ممكنة‬ ‫مسافة‬ ‫أقل‬ ‫في‬ ‫البداية‬ ‫نقطة‬
‫؟‬ ‫ممكنة‬ ‫مسافة‬ ‫أقل‬ ‫في‬ ‫البداية‬ ‫نقطة‬
•
Minimal spanning tree
Minimal spanning tree
•
In a telephone network we do not every subscriber
In a telephone network we do not every subscriber
to be connected directly to every other, as this would be
to be connected directly to every other, as this would be
very expansive. The cheapest network would be one in
very expansive. The cheapest network would be one in
which the graph is connected but with no cycles. This
which the graph is connected but with no cycles. This
will be a subgraph of our original graph called a
will be a subgraph of our original graph called a
spanning tree. A spanning tree is a subgraph of G that
spanning tree. A spanning tree is a subgraph of G that
includes every vertex of G and is a tree
includes every vertex of G and is a tree

18. Pick's Theorem
Pick's Theorem
1
2
B
A I
= + -

19. References
References
•
[
[
1
1
]
]
S. Barnett,
S. Barnett, Discrete Mathematics
Discrete Mathematics, Addison
, Addison
Wesley Longman 1998
Wesley Longman 1998
.
.
•
[
[
2
2
]
]
R. J. Wilson,
R. J. Wilson, Introduction to Graph Theory
Introduction to Graph Theory,
,
Longman Scientific and technical, 1986
Longman Scientific and technical, 1986
.
.