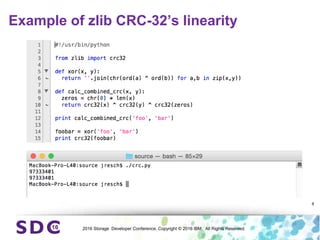
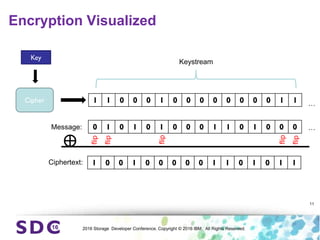
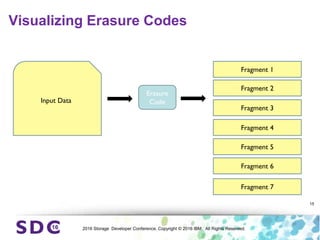
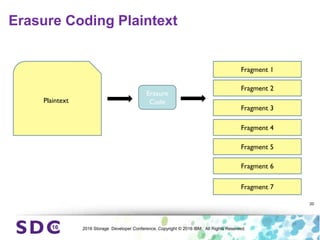
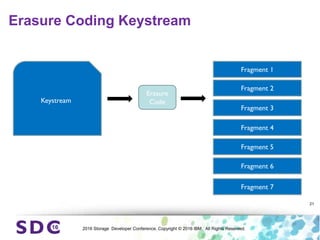
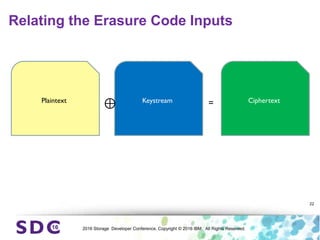
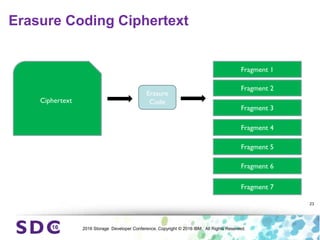
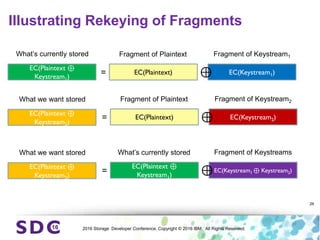
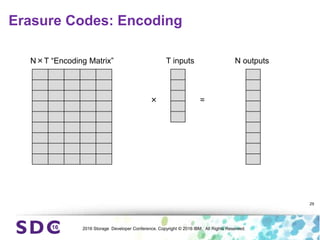
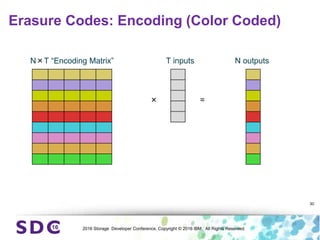
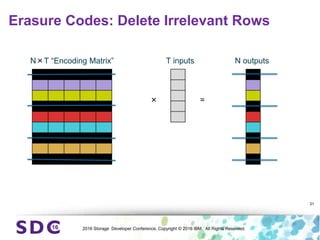
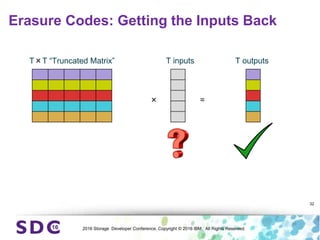
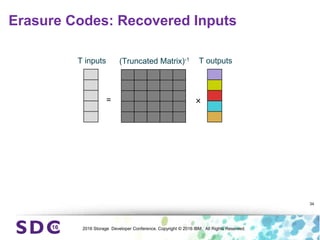
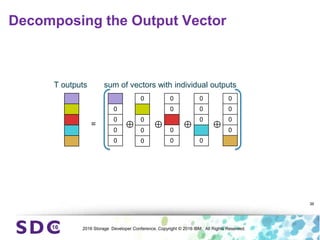
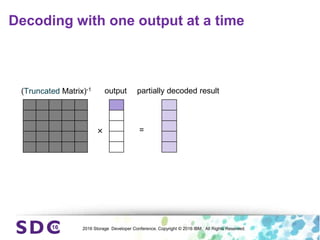
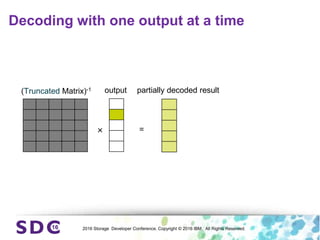
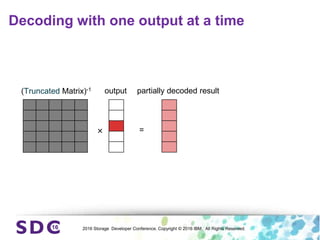
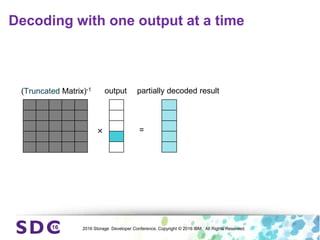
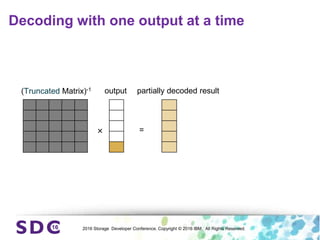
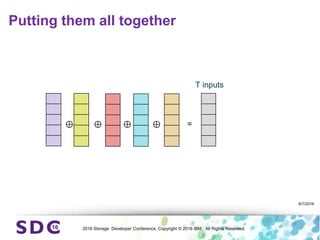
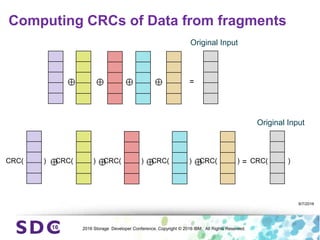
The document discusses how encryption and erasure codes are related through their use of linear functions. It explains that both encryption and erasure codes operate as linear functions in finite fields, allowing their outputs to be combined. This property allows encrypted or erasure coded data to be rekeyed or rebuilt without retrieving the original data. It also enables verifying integrity of erasure coded data without decoding it first. The document explores these applications and concludes that linearity opens opportunities for innovation in distributed storage systems.