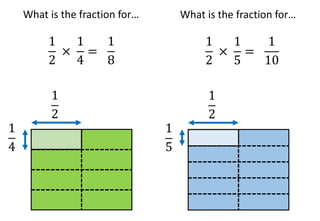
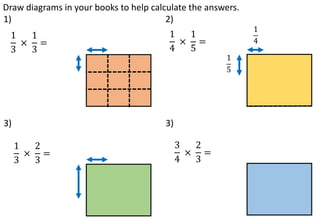
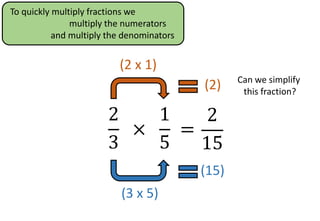
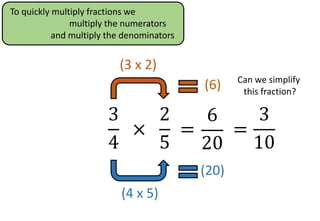
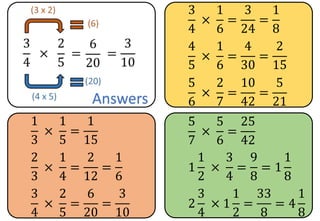
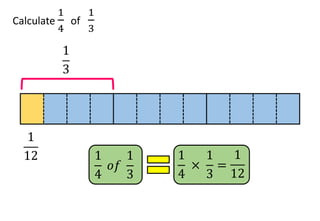
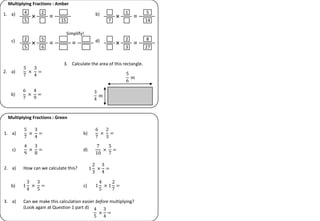
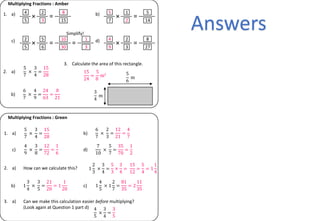
The document provides examples and step-by-step instructions for multiplying fractions, including multiplying fractions with numerators greater than 1, mixed numbers, and fractions of fractions. It emphasizes that to multiply fractions, one should multiply the numerators and multiply the denominators. The document concludes by asking the reader to assess their ability to multiply different types of fractions.

1. 16
x8
-5
÷10
x2 x5 +5 ÷5
-5
÷2
x3
10
??

2. 03 April 2023
Multiplying Fractions

3. 1
3
×
2
5
=
KNOWLEDGE CHECK
3
4
×
4
5
=
2
5
÷
1
6
=

4. 1
3
×
2
5
=
2
15
KNOWLEDGE CHECK
3
4
×
4
5
=
12
20
=
6
10
=
3
5
2
5
÷
1
6
=
12
5
= 2
2
5

5. Georgie took a
1
4
of the cake!
She split the piece into 3 and
gave one piece each to Tom and Rob.
How big was the piece Tom ate?
1
3
of
1
4
means
1
3
×
1
4
=
1
12

6. How do we find the area of a field?
8 metres
6 metres
Area = 8 × 6 = 48 metres2

7. What if we want to find the area of half the length,
and half the width?
4 metres
3 metres
We can see it is a quarter of the whole field.

8. What if we want to find the area of half the length,
and a third of the width?
What fraction of the field is the area?
1
4
1
5
1
6
or or ?

9. 1
2
×
1
3
=
1
6
1
2
1
3
This is an easy way to multiply fractions.

10. What is the fraction for…
1
2
×
1
4
=
1
2
1
4
1
8
What is the fraction for…
1
2
×
1
5
=
1
2
1
5
1
10

11. What is the fraction for…
1
3
×
1
4
=
1
3
1
4
1
12
What is the fraction for…
2
3
×
1
4
=
2
3
1
4
2
12

12. Draw diagrams in your books to help calculate the answers.
1
3
×
1
3
=
1
4
×
1
5
=
1
5
1
3
×
2
3
=
3
4
×
2
3
=
1) 2)
3) 3)
1
4

13. Draw diagrams in your books to help calculate the answers.
1
3
×
1
3
=
1
9
1
3
1
4
×
1
5
=
1
20
1
4
1
5
1
3
×
2
3
=
2
9
1
3
2
3
3
4
×
2
3
=
6
12
3
4
2
3
Can we make
this fraction simpler?
1) 2)
3) 3)
1
3
Answers

14. Draw diagrams in your books to help calculate the answers.
1
3
×
1
3
=
1
9
1
3
1
4
×
1
5
=
1
20
1
4
1
5
1
3
×
2
3
=
2
9
1
3
2
3
3
4
×
2
3
=
6
12
3
4
2
3
Can we make
this fraction simpler?
1) 2)
3) 3)
1
3
Answers
Can we write a rule for multiplying fractions,
just using numbers?

15. 1
3
×
2
3
=
2
9
1
3
2
3
To multiply fractions,
multiply the numerator,
then multiply the denominator.
ANNA says….
Is Anna right?

16. 1
2
×
1
3
=
(2 x 3)
(1 x 1)
To quickly multiply fractions we
multiply the numerators
and multiply the denominators
(1)
(6)
1
6

17. 1
3
×
2
3
=
(3 x 3)
(1 x 2)
To quickly multiply fractions we
multiply the numerators
and multiply the denominators
(2)
(9)
2
9

18. 1
4
×
2
3
=
(4 x 3)
(1 x 2)
To quickly multiply fractions we
multiply the numerators
and multiply the denominators
(2)
(12)
2
12
Can we simplify
this fraction?
=
1
6

19. 2
3
×
1
5
=
(3 x 5)
(2 x 1)
To quickly multiply fractions we
multiply the numerators
and multiply the denominators
(2)
(15)
2
15
Can we simplify
this fraction?

20. 3
4
×
2
5
=
(4 x 5)
(3 x 2)
To quickly multiply fractions we
multiply the numerators
and multiply the denominators
(6)
(20)
6
20
Can we simplify
this fraction?
=
3
10

21. 5
6
×
3
5
=
(6 x 5)
(5 x 3)
To quickly multiply fractions we
multiply the numerators
and multiply the denominators
(15)
(30)
15
30
Can we simplify
this fraction?
=
1
2

22. What’s wrong? What’s the answer?
2
3
×
4
5
=
6
15
2
3
×
3
5
=
6
15
Sarah
Julie
8
15
2
5

23. 1
3
×
1
5
=
2
3
×
1
4
=
3
4
×
2
5
=
3
4
×
1
6
=
4
5
×
1
6
=
5
6
×
2
7
=
5
7
×
5
6
=
1
1
2
×
3
4
=
2
3
4
× 1
1
2
=

24. 1
3
×
1
5
=
1
15
2
3
×
1
4
=
2
12
=
1
6
3
4
×
2
5
=
6
20
=
3
10
3
4
×
1
6
=
3
24
=
1
8
4
5
×
1
6
=
4
30
=
2
15
5
6
×
2
7
=
10
42
=
5
21
5
7
×
5
6
=
25
42
1
1
2
×
3
4
=
9
8
= 1
1
8
2
3
4
× 1
1
2
=
33
8
= 4
1
8
Answers

25. Ben, Bob and Bill split a pizza equally.
What fraction of the whole Pizza did Anna get?
Ben
Anna
Bob Bill
Ben gave half his pizza to
his sister, Anna.
Anna got
1
6
of the whole pizza.
1
2
𝑜𝑓
1
3
1
2
×
1
3
=
1
6

26. Jim, Jane, Jack and John split a pizza equally.
What fraction of the whole Pizza did David get?
Jim
David
Jim gave half his pizza to
his brother, David.
David got
1
8
of the whole pizza.
1
2
𝑜𝑓
1
4
1
2
×
1
4
=
1
8
Jane Jack John

27. 1
2
𝑜𝑓
1
8
1
2
×
1
8
=
1
16
Mary split her birthday cake into 8 equal pieces.
What fraction of the whole cake is
one of Sally’s pieces?
Sally split one of the pieces into two.
1
8
1
16

28. 1
3
𝑜𝑓
1
7
1
3
×
1
7
=
1
21
Mary split her birthday cake into 7 equal pieces.
What fraction of the whole cake is
one of Sally’s pieces?
Sally split one of the pieces into 3.
1
7
1
21

29. 1
3
𝑜𝑓
1
2
1
3
×
1
2
=
1
6
Calculate
1
3
of
1
2
1
3
1
6

30. 1
4
𝑜𝑓
1
3
1
4
×
1
3
=
1
12
Calculate
1
4
of
1
3
1
3
1
12

31. 1
4
𝑜𝑓
2
3
1
4
×
2
3
=
2
12
Calculate
1
4
of
2
3
2
3
1
12
1
12
=
1
6

32. 3
4
𝑜𝑓
2
3
3
4
×
2
3
=
6
12
Calculate
3
4
of
2
3
2
3
1
12
1
12
=
1
2
1
12
1
12
1
12
1
12

33. Draw diagrams in your books to help calculate the answers.
1
2
of
1
3
=
1
5
of
1
2
=
2
5
of
1
4
=
1
3
of
2
3
=
2
3
of
3
4
=
4
5
of
3
4
=

34. Draw diagrams in your books to help calculate the answers.
1
2
of
1
3
=
1
6
1
5
of
1
2
=
1
10
2
5
of
1
4
=
2
20
=
2
20
1
3
of
2
3
=
2
9
2
3
of
3
4
=
6
12
=
1
2
4
5
of
3
4
=
12
20
=
3
5

35. 1. a)
Multiplying Fractions : Amber
× =
4
5
2
15
b)
× =
7
1 5
14
c)
× =
2
5
5
6
d)
× =
2
3
8
27
5
7
×
3
4
=
2. a)
6
7
×
4
9
=
b)
5
6
m
3
4
m
3. Calculate the area of this rectangle.
=
Multiplying Fractions : Green
5
7
×
3
4
=
1. a)
6
7
×
2
3
=
b)
4
9
×
3
8
=
c)
7
10
×
5
7
=
d)
1
2
3
×
3
4
=
2. a) How can we calculate this?
1
3
4
×
3
5
=
b) 1
4
5
× 1
2
7
=
c)
3. a) Can we make this calculation easier before multiplying?
(Look again at Question 1 part d) 4
5
×
3
4
=
Simplify!
1. a)
Multiplying Fractions : Amber
× =
4
5
2
15
b)
× =
7
1 5
14
c)
× =
2
5
5
6
d)
× =
2
3
8
27
5
7
×
3
4
=
2. a)
6
7
×
4
9
=
b)
5
6
m
3
4
m
3. Calculate the area of this rectangle.
=
Multiplying Fractions : Green
5
7
×
3
4
=
1. a)
6
7
×
2
3
=
b)
4
9
×
3
8
=
c)
7
10
×
5
7
=
d)
1
2
3
×
3
4
=
2. a) How can we calculate this?
1
3
4
×
3
5
=
b) 1
4
5
× 1
2
7
=
c)
3. a) Can we make this calculation easier before multiplying?
(Look again at Question 1 part d) 4
5
×
3
4
=
Simplify!

36. 1. a)
Multiplying Fractions : Amber
× =
4
5
2
15
b)
× =
7
1 5
14
c)
× =
2
5
5
6
d)
× =
2
3
8
27
5
7
×
3
4
=
2. a)
6
7
×
4
9
=
b)
5
6
m
3
4
m
3. Calculate the area of this rectangle.
=
Multiplying Fractions : Green
5
7
×
3
4
=
1. a)
6
7
×
2
3
=
b)
4
9
×
3
8
=
c)
7
10
×
5
7
=
d)
1
2
3
×
3
4
=
2. a) How can we calculate this?
1
3
4
×
3
5
=
b) 1
4
5
× 1
2
7
=
c)
3. a) Can we make this calculation easier before multiplying?
(Look again at Question 1 part d) 4
5
×
3
4
=
Simplify!

37. 1. a)
Multiplying Fractions : Amber
× =
4
5
2
3
8
15
b)
× =
5
7
1
2
5
14
c)
× =
2
5
5
6
10
30
d)
× =
4
9
2
3
8
27
5
7
×
3
4
=
15
28
2. a)
6
7
×
4
9
=
24
63
=
8
21
b)
5
6
m
3
4
m
3. Calculate the area of this rectangle.
=
1
3
15
24
=
5
8
m2
Multiplying Fractions : Green
5
7
×
3
4
=
15
28
1. a)
6
7
×
2
3
=
12
21
=
4
7
b)
4
9
×
3
8
=
12
72
=
1
6
c)
7
10
×
5
7
=
35
70
=
1
2
d)
1
2
3
×
3
4
=
5
3
×
3
4
=
15
12
=
5
4
= 1
1
4
2. a) How can we calculate this?
1
3
4
×
3
5
=
21
20
= 1
1
20
b) 1
4
5
× 1
2
7
=
81
35
= 2
11
35
c)
3. a) Can we make this calculation easier before multiplying?
(Look again at Question 1 part d) 4
5
×
3
4
=
3
5
Simplify!
Answers

38. Answers

39. Answers

40. Georgie took a
1
5
of the cake!
She split the piece into 4 and
gave one piece to Tom, Ann and Rob.
How big was the piece Ann got?
1
4
of
1
5
means
1
4
×
1
5
=
1
20

41. I can multiply fractions with 1 as the numerator.
I can multiply fractions with any numerator.
I can multiply mixed numbers.
Check your success!

42. I can multiply fractions with 1 as the numerator.
I can multiply fractions with any numerator.
I can multiply mixed numbers.
Check your success!

43. Write a text message to a friend describing…
How to multiply
fractions.

44. Questions?
Comments?
Suggestions?
…or have you found a mistake!?
Any feedback would be appreciated .
Please feel free to email:
tom@goteachmaths.co.uk