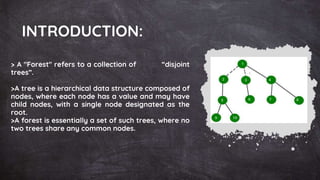
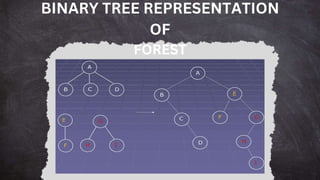
This document discusses forests in data structures. A forest refers to a collection of disjoint trees, where no two trees share any common nodes. The document defines forests and provides examples. It also discusses how to transform a forest into a binary tree by linking the binary tree representations of each tree in the forest. Finally, it describes how to perform preorder, inorder, and postorder traversals on a forest by traversing the corresponding binary tree.

1. ATRIA INSTITUTE OF TECHNOLOGY
BANGALORE-54, Karnataka
DEPARTMENT OF COMPUTER SCIENCE & ENGINEERING (Data Science)
DSA Seminar On
“FORESTS”
VISVESVARAYA TECHNOLOGICAL UNIVERSITY
“Jnana Sangama”, Belagavi– 590018
PRESENTED BY
Mohammed Zaidaan Shiraz(1AT22CD033)
Safeen Ahmed(1AT22CD047)
UNDER THE GUIDANCE OF
Dr. K S Ananda Kumar
Associate Professor
Dept. of ISE, Atria IT

2. INTRODUCTION
TO FORESTS
IN DATA STRUCTURES

3. CONTENTS:
> Definition.
> Three Tree Forest.
> Transforming a Forest into a Binary Tree.
> Forest Traversals.
> Preorder Traversal.
> Inorder Traversal.
> Postorder Traversal.

4. > A "Forest" refers to a collection of “disjoint
trees”.
>A tree is a hierarchical data structure composed of
nodes, where each node has a value and may have
child nodes, with a single node designated as the
root.
>A forest is essentially a set of such trees, where no
two trees share any common nodes.
INTRODUCTION:

5. DEFINITION:
> The collection of zero or more trees is called Forest
> A forest is a set of n>=0 disjoint trees.
> The concept of a forest is very close to that of a
tree because if we remove the root of a tree, we
obtain a forest.
> For example, removing the root of any binary tree
produces a forest of two trees.

6. Three-Tree
Forest

7. TRANSFORMING A FOREST INTO A BINARY
TREE
> To transform a forest into a single binary tree, we
first obtain the binary tree representation of each
of the trees in the forest and then link these binary
trees together through the right Child field of the
root nodes.

8. BINARY TREE REPRESENTATION
OF
FOREST

9. We can define this transformation in
a formal way as follows:
>Definition: If T1, . . . , Tn is a forest of trees, then
the binary tree corresponding to this forest,
denoted by B(T1, . . . , Tn),
> 1. is empty if n=0
> 2. has root equal to root (T1); has left subtree
equal to B(T11, T12, . . . , T1m), where T11, . . . ,
T1m are the subtreesof root(T1); and has right
subtree B(T2, . . . , Tn).

10. FOREST TRAVERSALS
>The Forest can be traversed using following three
methods:
1. Preorder traversal
2. Inorder traversal
3. Postorder traversal
>Preorder and inorder traversals of the
corresponding binary tree T of a forest F have a
natural correspondence to traversals on F.

11. Preorder Traversal
>Preorder traversal of T is equivalent to
visiting
the nodes of F in forest preorder, which is
defined as follows:
1.If F is empty then return.
2.Visit the root of the first tree of F.
3.Traverse the subtrees of the first tree in
forest preorder
4.Traverse the remaining trees of F in forest
preorder.

12. InOrder Traversal
>InOrder Traversal of T is equivalent to
visiting the nodes of F in forest inorder,
which is defined as follows:
1.If F is empty then return.
2.Traverse the subtrees of the first tree in
forest inorder.
3.Visit the root of the first tree.
4.Traverse the remaining trees in forest
inorder

13. Postorder Traversal
We can define the postorder traversal of a
forest as follows:
1.If F is empty then return
2.Traverse the subtrees of the first tree of F in
forest postorder.
3.Traverse the remaining trees of F in forest
postorder.
4.Visit the root of the first tree of F.

14. THANK YOU
VERY MUCH!