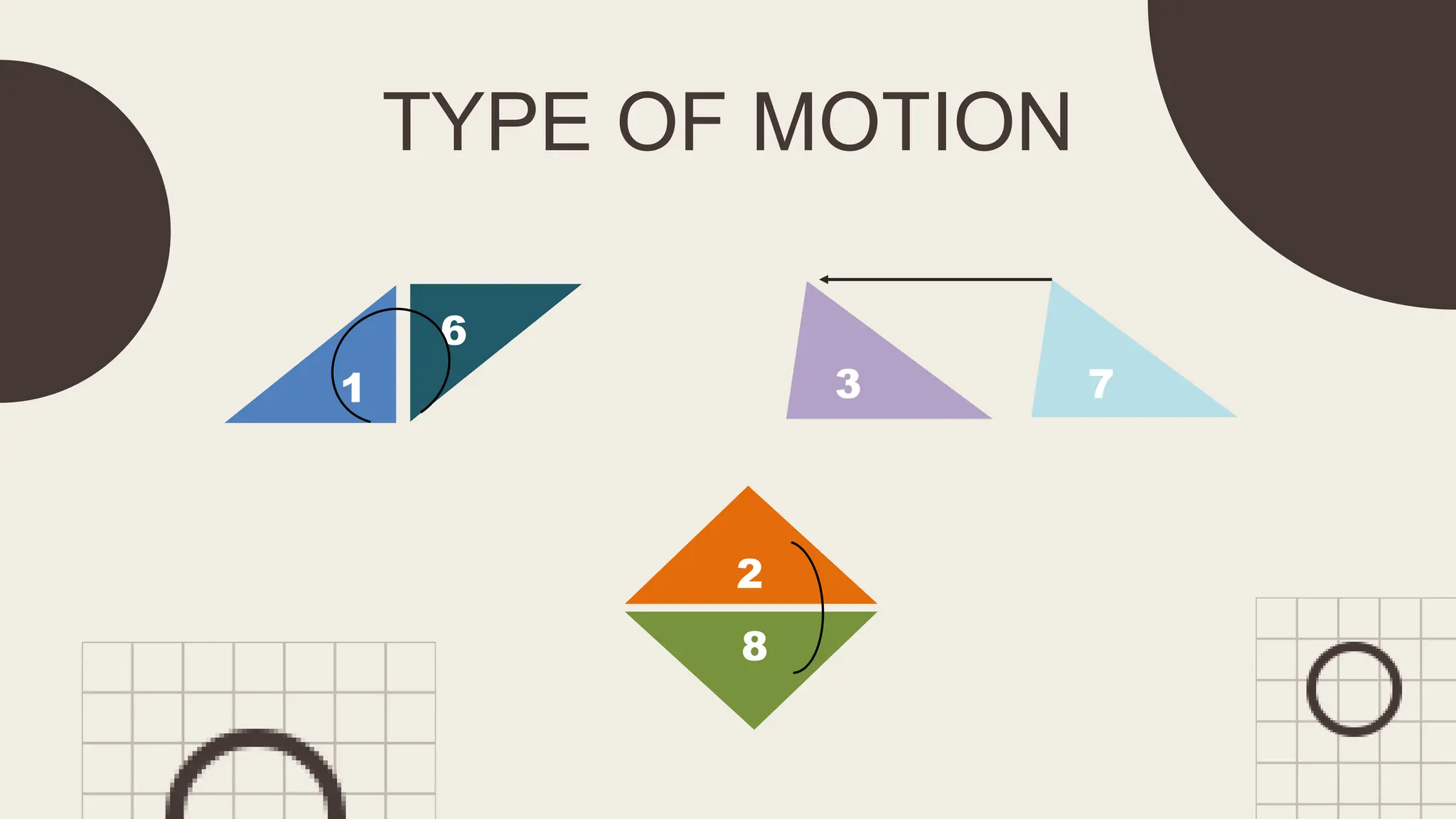
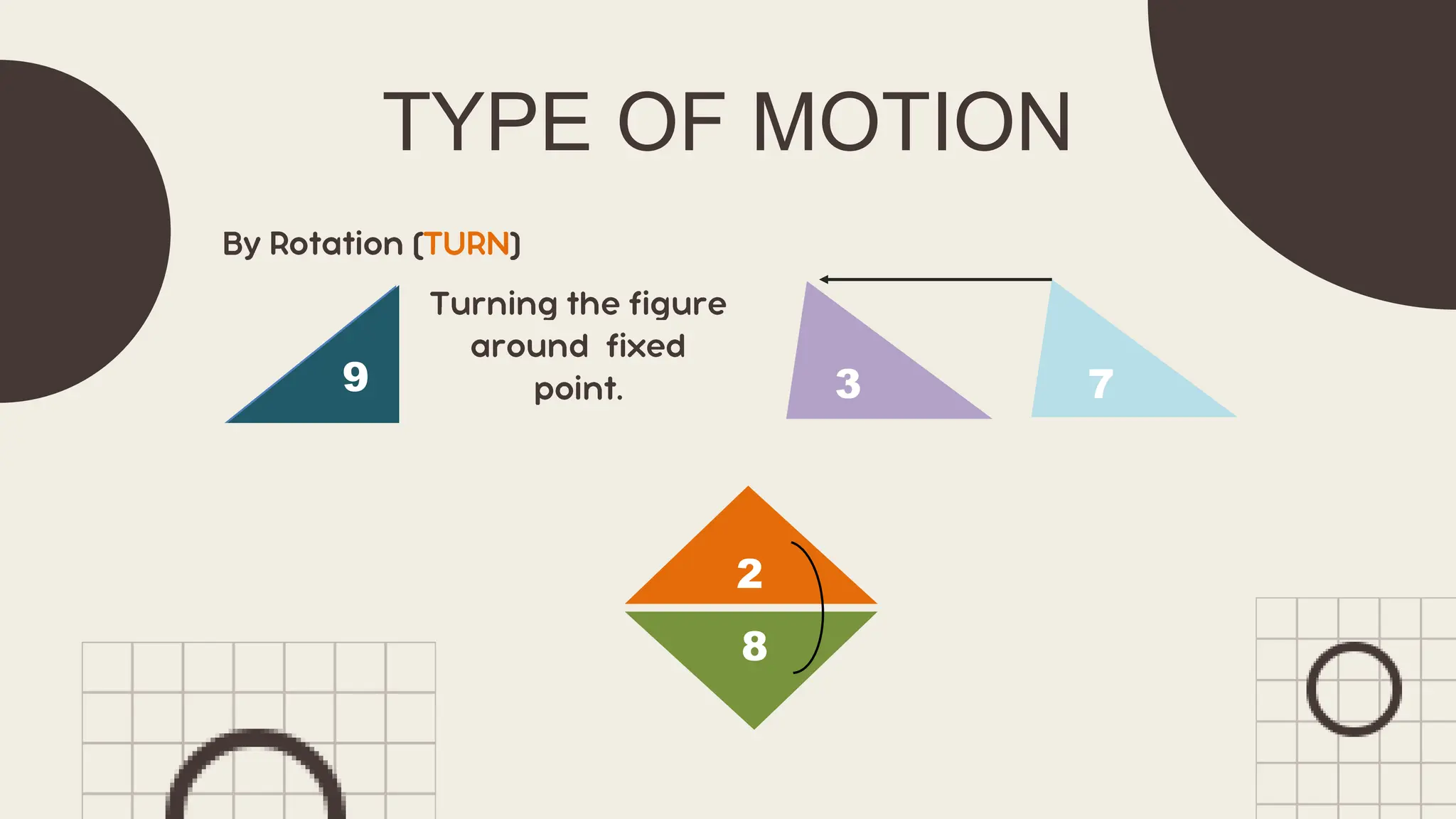
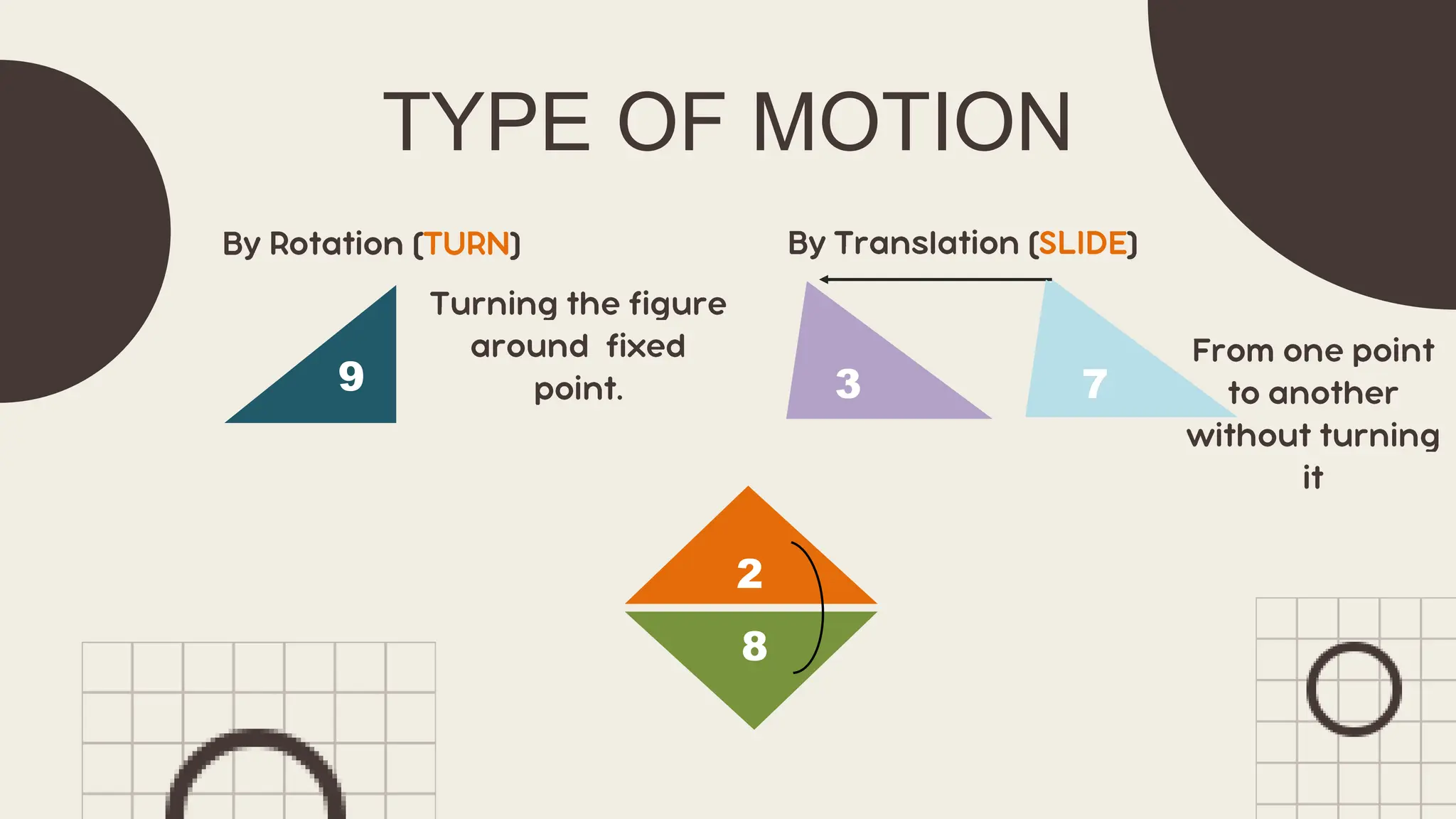
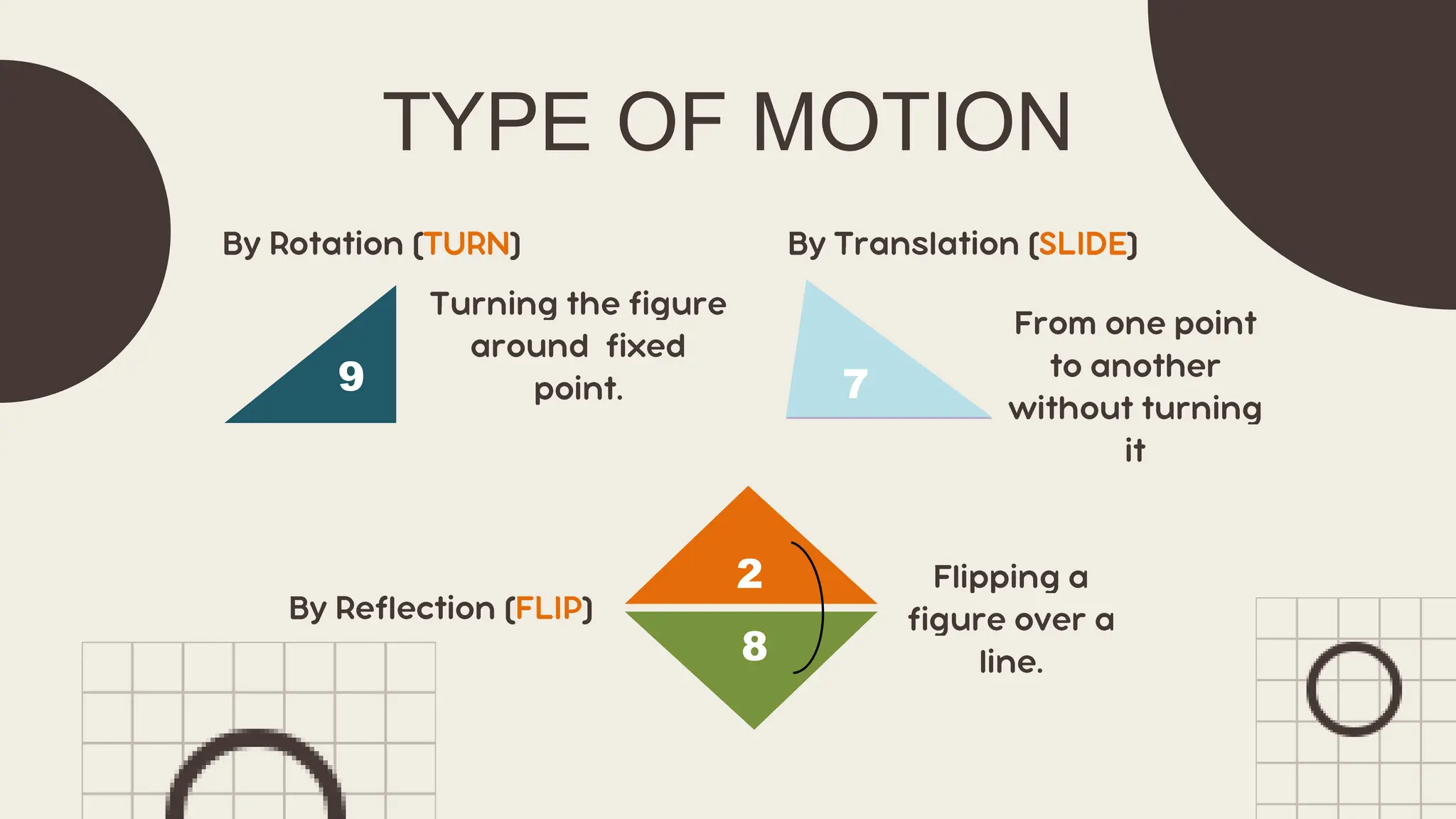
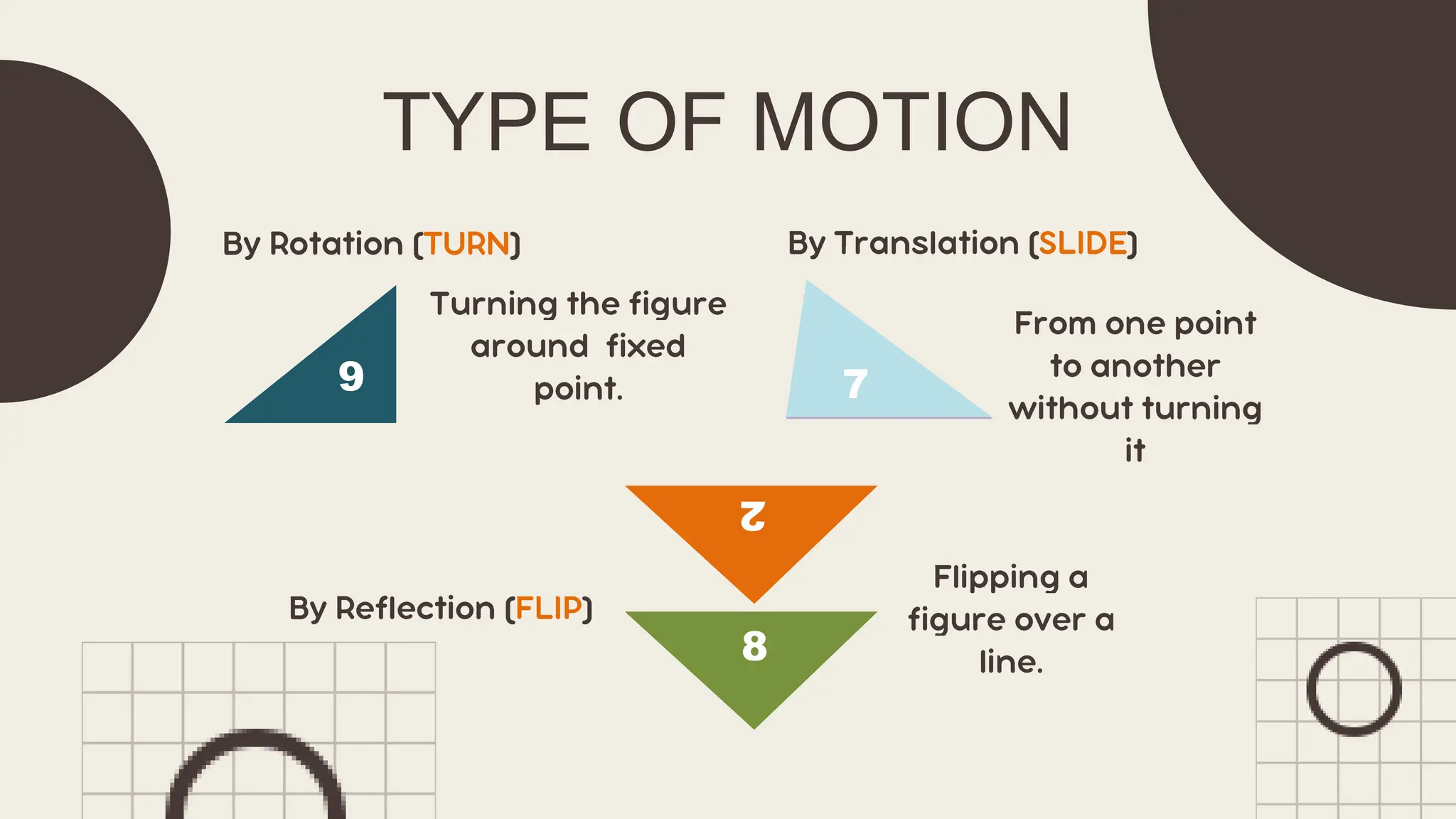
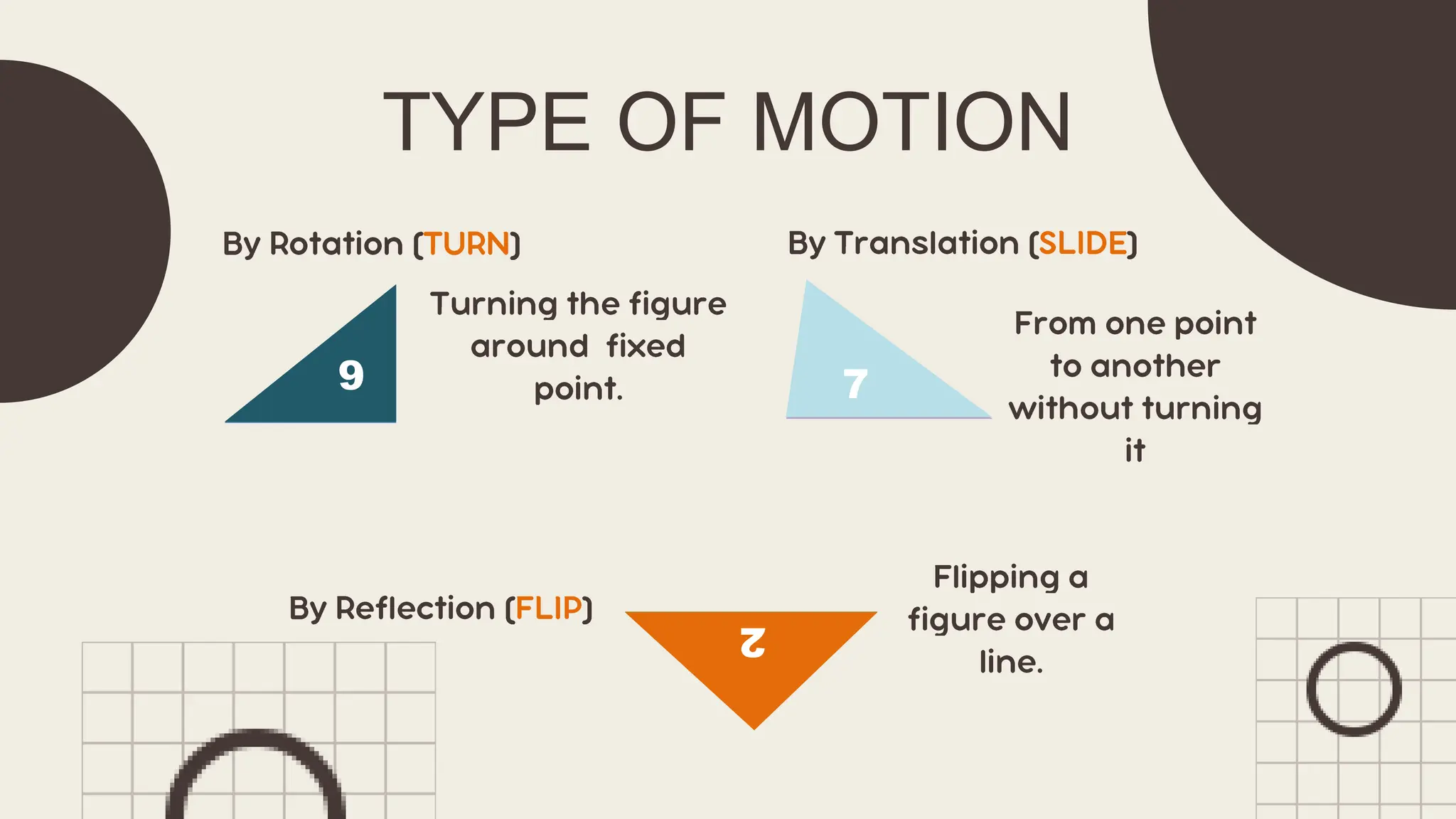
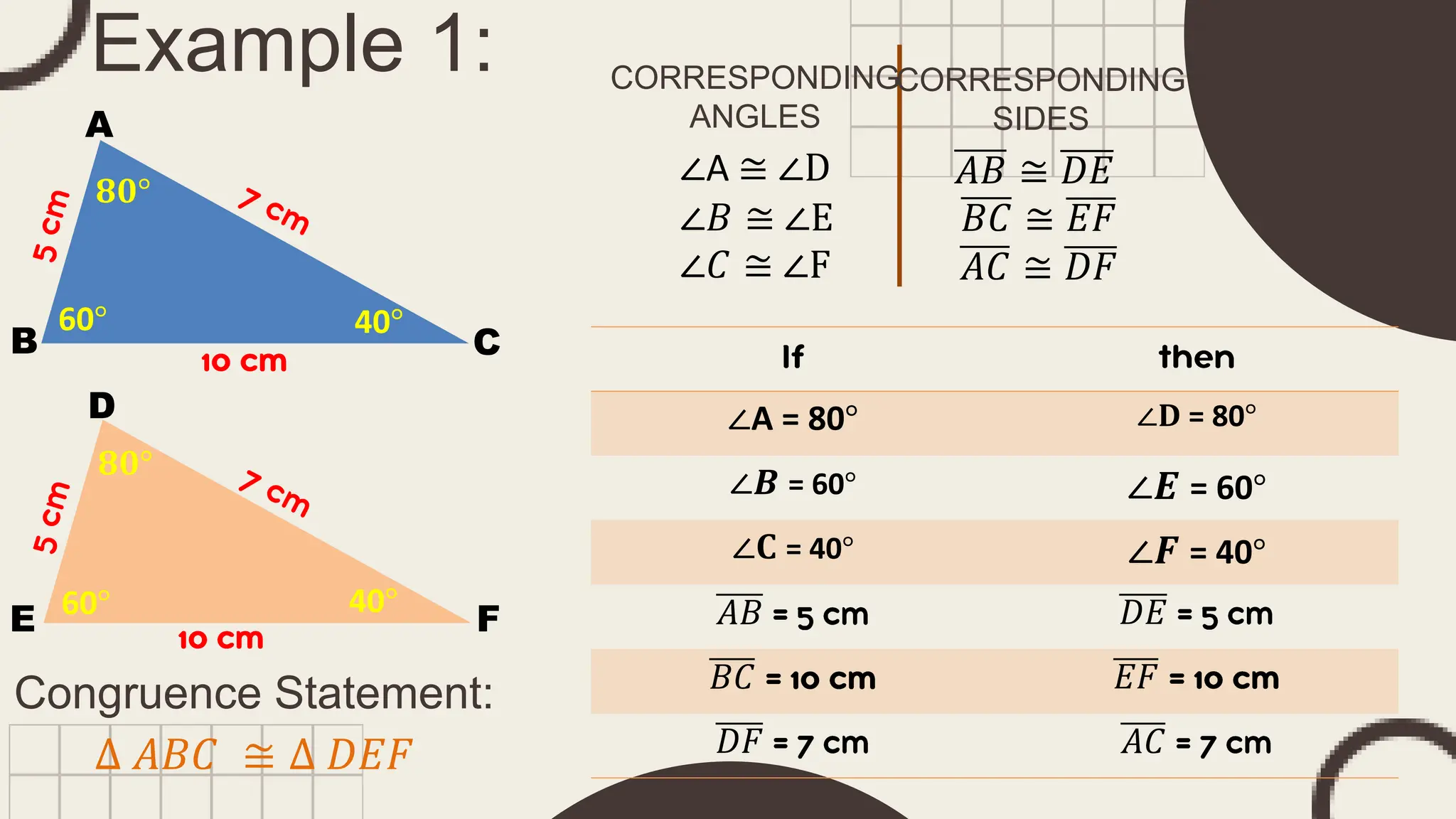
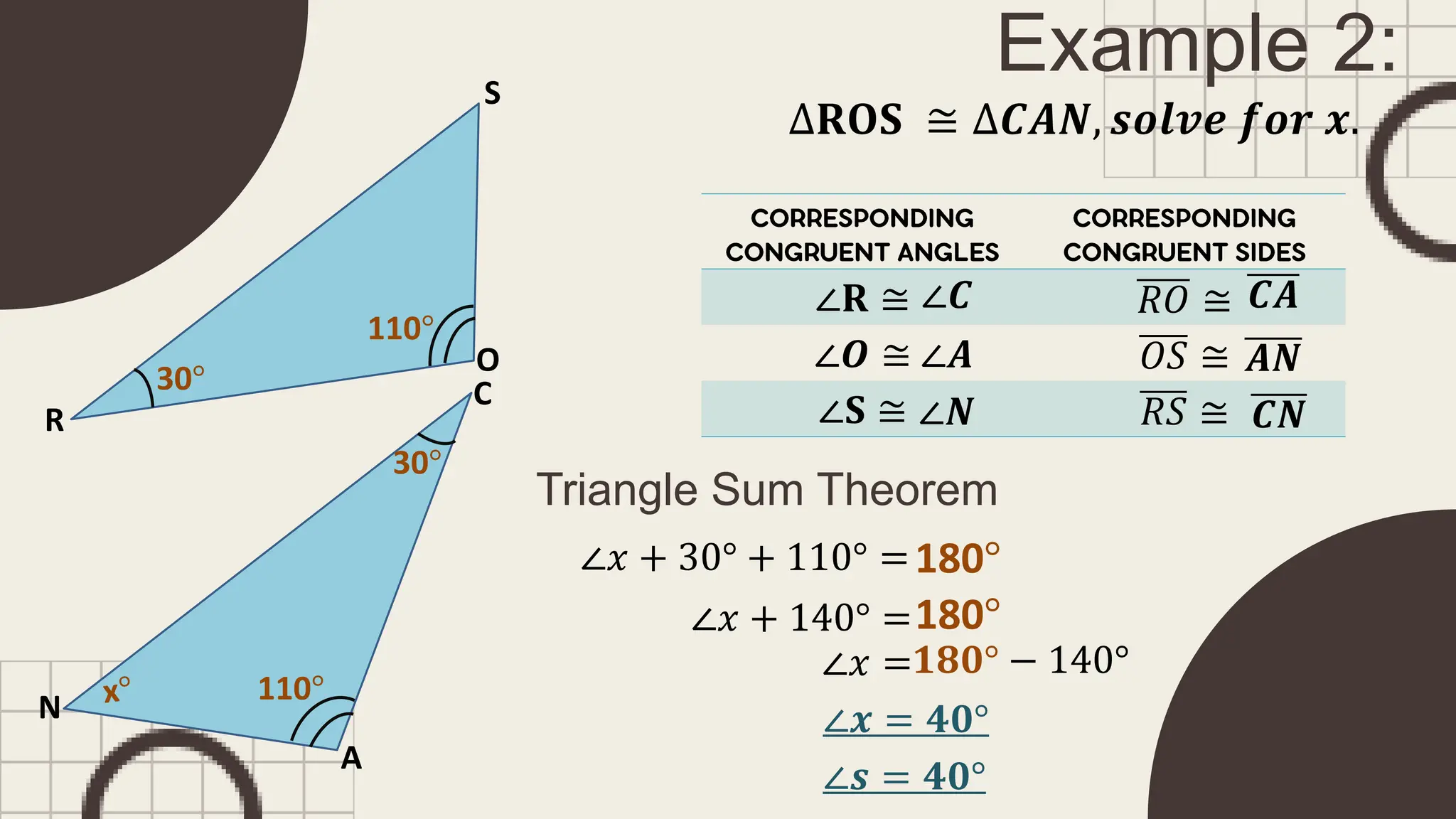
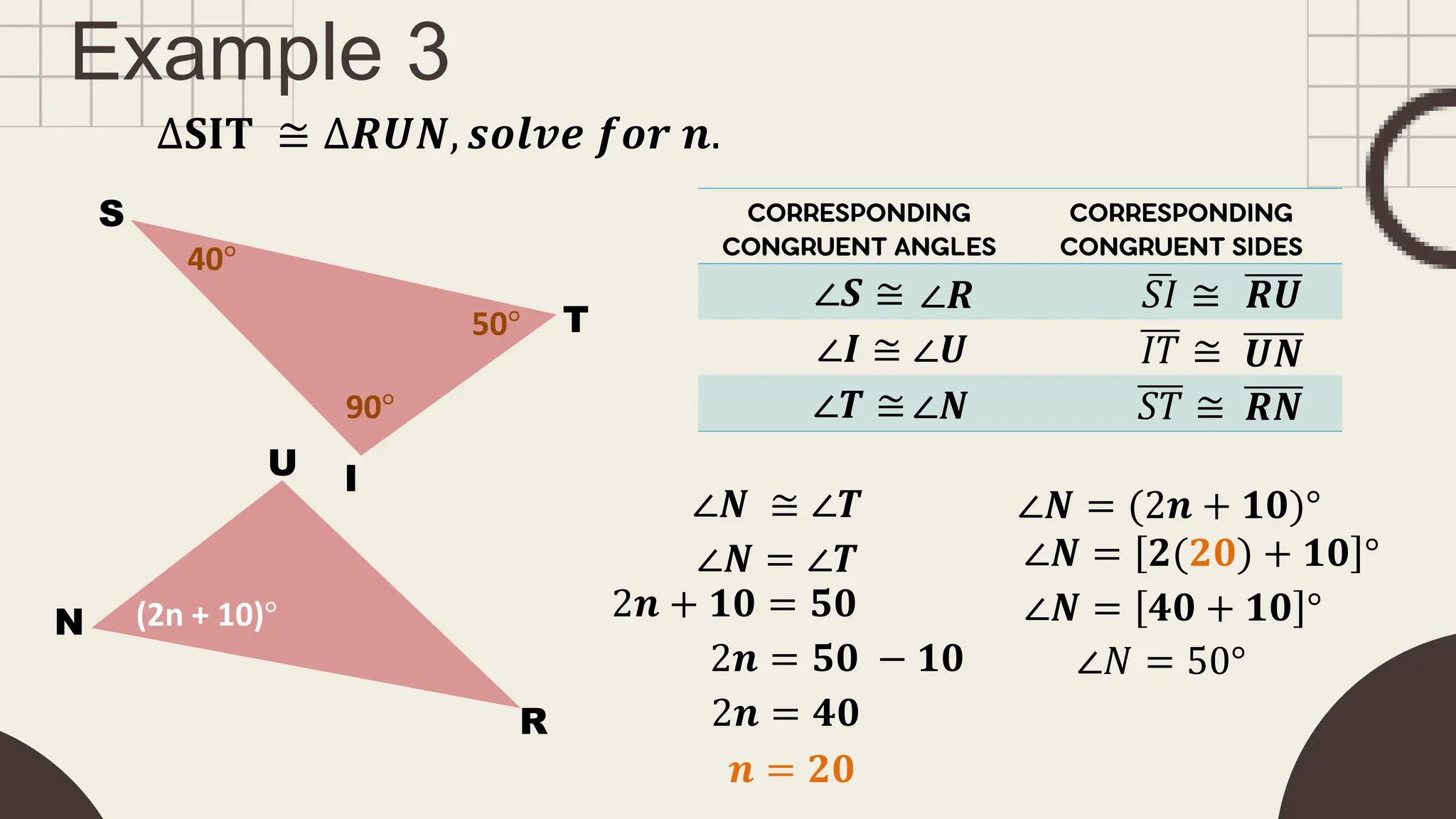
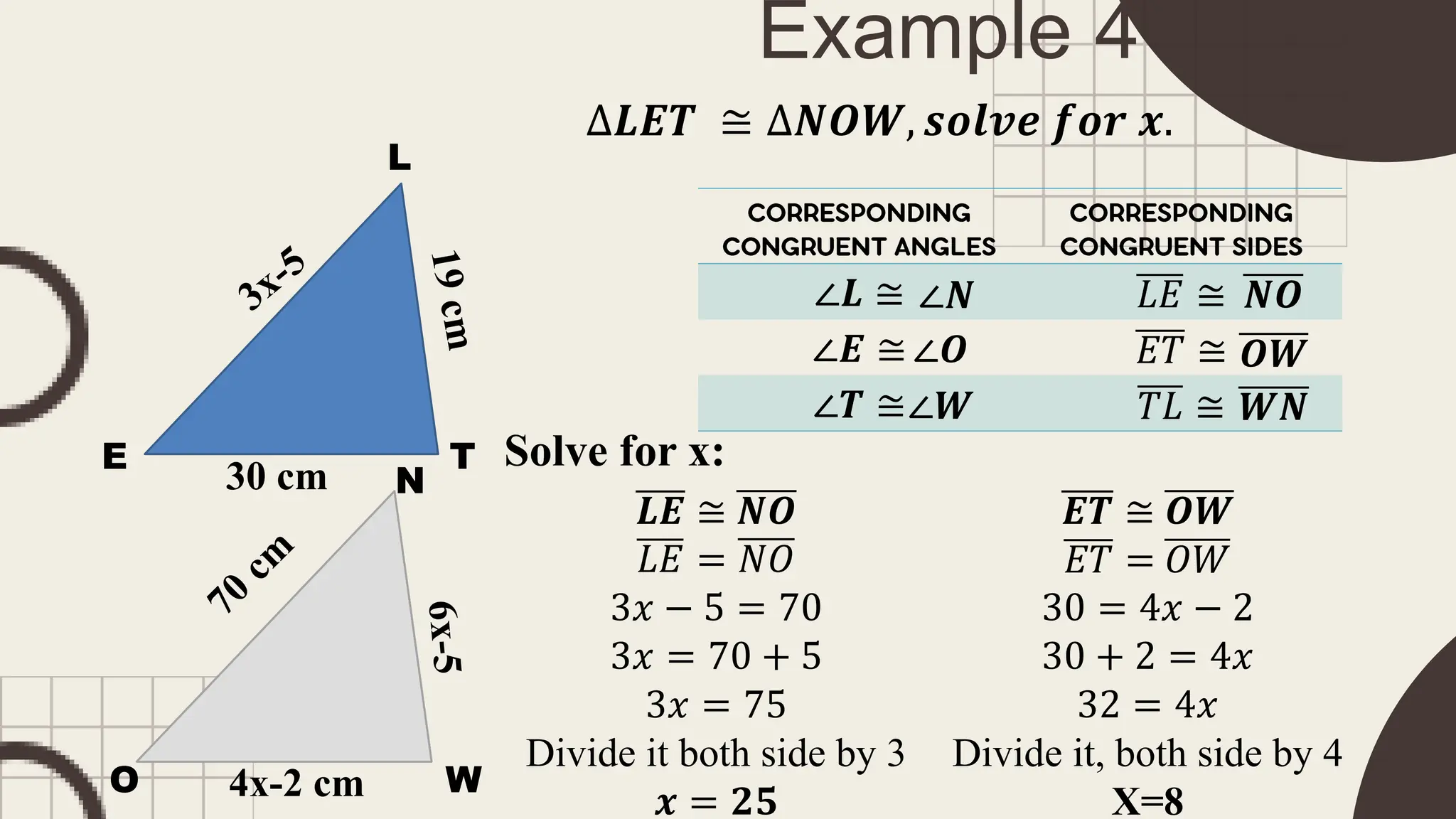
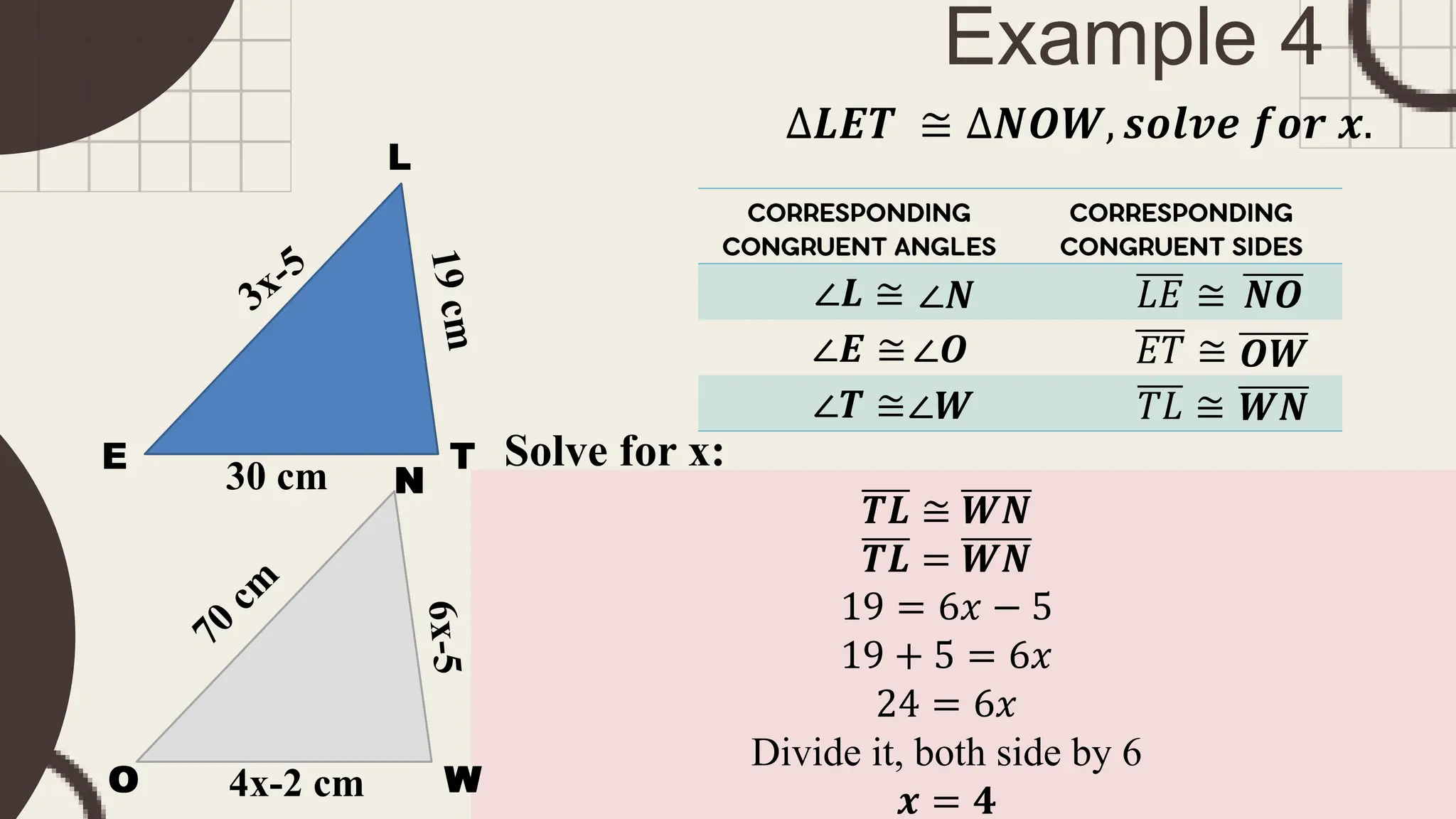
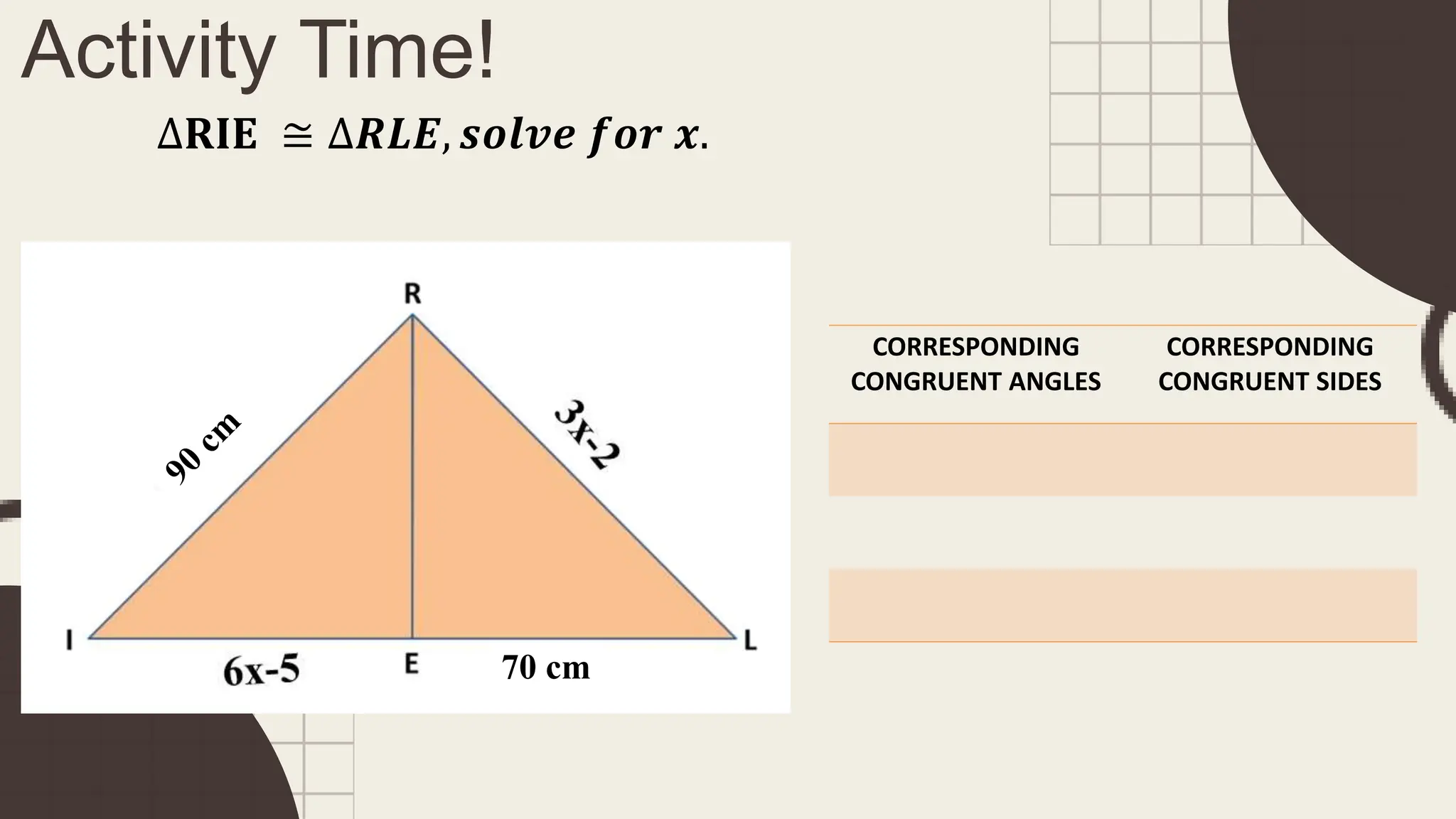
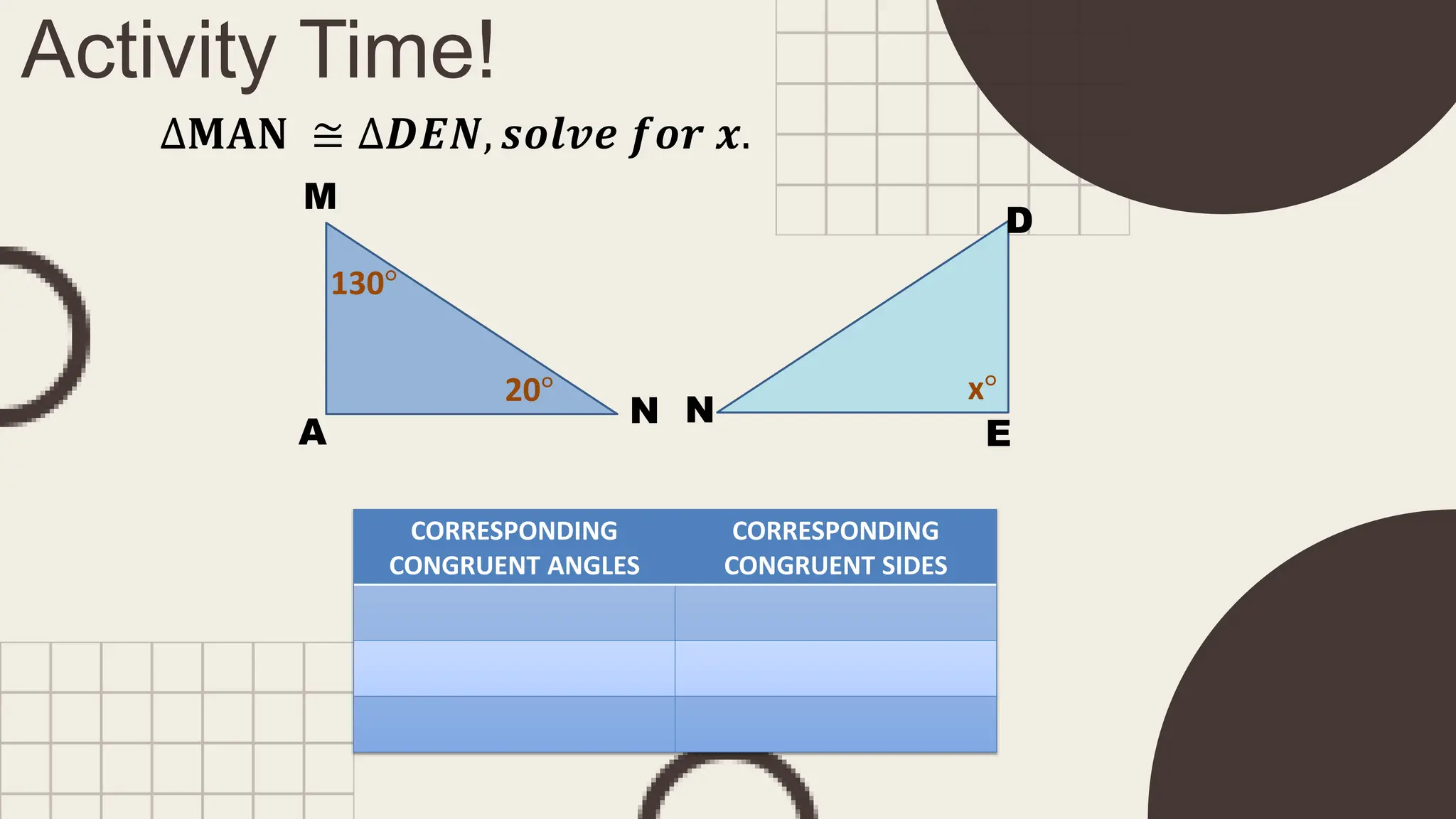
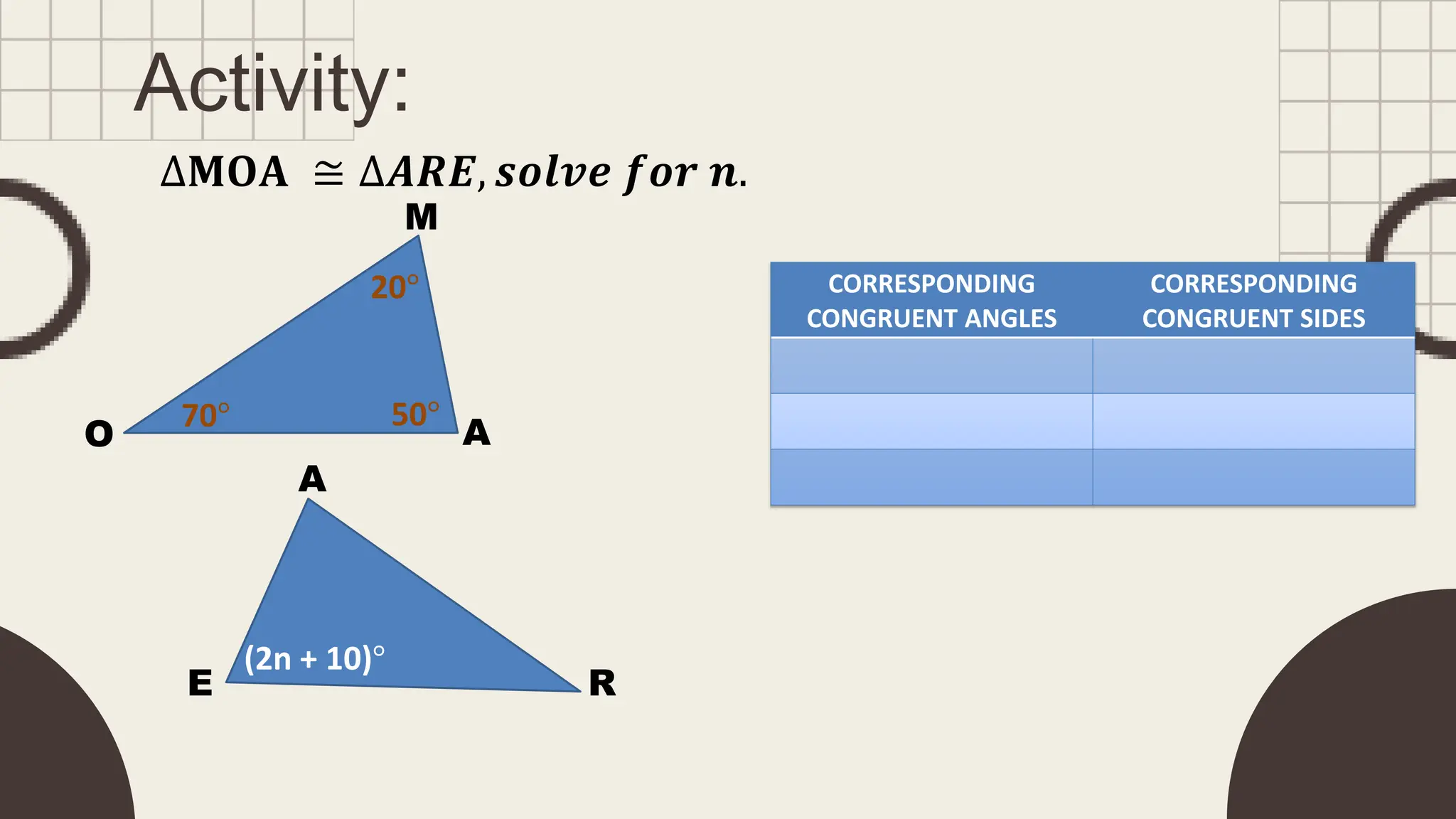
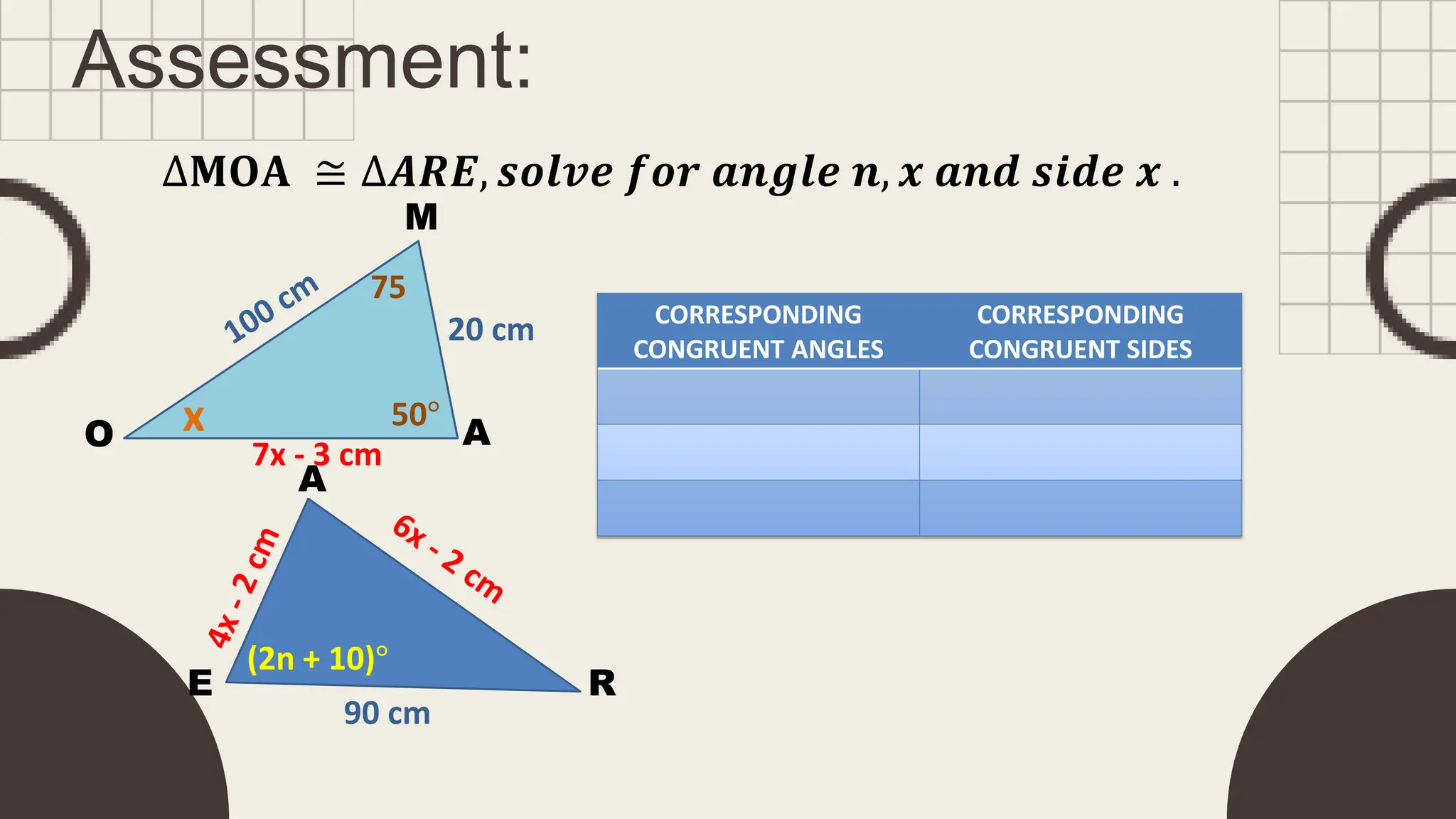
The document outlines principles of congruent triangles, detailing how two triangles are congruent based on the equality of their corresponding sides and angles. It provides examples and practice problems for students to solve using congruence statements and the triangle sum theorem. The document serves as both a lesson introduction and practice material for students learning about triangle congruence.

4. Activity
1 3 2
8
7 4
6
5
9

5. Activity:
1 3 2
8 7 4
6
5
9

6. Activity:
1 3 2
8
7
4
6
5
9

7. Activity:
1 3 2
8
7
4
6
5
9

8. Activity:
1 3 2
8
7
4
6
5 9

9. Activity:
1 3 2
8
7
4
6
5 9

10. Activity:
1 3 2
8
7
4
6
5

11. SOLVING
CORRESPONDING
CONGRUENT
TRIANGLE

12. Welcome To
Class!
Today’s Objectives:

13. When we can say that the
triangle are congruent?

14. Two triangle are congruent when their
corresponding sides are equal in length,
and their corresponding angles are equal
in measure.

15. TYPES OF MOTION

16. TYPE OF MOTION
1 3
8
7
6
2

17. TYPE OF MOTION
1 3
8
7
6
2

18. TYPE OF MOTION
1 3 7
7
6
8
2

19. TYPE OF MOTION
1 3
7
6
8
2

20. TYPE OF MOTION
1 3
7
6
8
2

21. TYPE OF MOTION
1 3
7
6
8
2

22. CONGRUENT TRIANGLE
B
A
C F
E
D
∠A↔ _____
∠𝐵 ↔_____
∠𝐶 ↔ _____
CORRESPONDING
ANGLES
CORRESPONDING SIDES
∠D
∠E
∠F
𝐴𝐵 ↔ ______
𝐵𝐶 ↔ ______
𝐴𝐶 ↔ ______
𝐷𝐸
𝐸𝐹
𝐷𝐹
∠A ≅ ∠D
∠𝐵 ≅ ∠E
∠𝐶 ≅ ∠F
𝐴𝐵 ≅ 𝐷𝐸
𝐵𝐶 ≅ 𝐸𝐹
𝐴𝐶 ≅ 𝐷𝐹
Congruence Statement: ∆ 𝐴𝐵𝐶 ≅ ∆ 𝐷𝐸𝐹

23. Example 1:
B
A
C
F
E
D
∠A ≅ ∠D
∠𝐵 ≅ ∠E
∠𝐶 ≅ ∠F
𝐴𝐵 ≅ 𝐷𝐸
𝐵𝐶 ≅ 𝐸𝐹
𝐴𝐶 ≅ 𝐷𝐹
CORRESPONDING
ANGLES
CORRESPONDING
SIDES
Congruence Statement:
∆ 𝐴𝐵𝐶 ≅ ∆ 𝐷𝐸𝐹
∠A = 80° ∠𝐃 = 80°
∠𝑩 = 60° ∠𝑬 = 60°
∠𝐂 = 40° ∠𝑭 = 40°
𝐴𝐵 𝐷𝐸
𝐵𝐶 𝐸𝐹
𝐷𝐹 𝐴𝐶
𝟖𝟎°
𝟖𝟎°
60°
60°
40°
40°

24. Example 2:
∆𝐑𝐎𝐒 ≅ ∆𝑪𝑨𝑵, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒙.
C
N
A
∠𝐑 ≅ 𝑅𝑂 ≅
∠𝑶 ≅ 𝑂𝑆 ≅
∠𝐒 ≅ 𝑅𝑆 ≅
∠𝑨
∠𝑵
𝑪𝑨
𝑨𝑵
𝑪𝑵
30°
110°
∠𝑥 + 30° + 110° =
Triangle Sum Theorem
180°
∠𝑥 + 140° =180°
∠𝑥 =𝟏𝟖𝟎° − 140°
∠𝒙 = 𝟒𝟎°
∠𝑪
R
S
O
30°
110°
∠𝒔 = 𝟒𝟎°

25. Example 3
∆𝐒𝐈𝐓 ≅ ∆𝑹𝑼𝑵, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒏.
R
N
U I
T
S
40°
90°
50°
(2n + 10)°
∠𝑺 ≅ 𝑆𝐼 ≅
∠𝑰 ≅ 𝐼𝑇 ≅
∠𝑻 ≅ 𝑆𝑇 ≅
∠𝑹
∠𝑼
∠𝑵
𝑹𝑼
𝑼𝑵
𝑹𝑵
∠𝑵 ≅ ∠𝑻
∠𝑵 = ∠𝑻
2𝒏 + 𝟏𝟎 = 𝟓𝟎
2𝒏 = 𝟓𝟎 − 𝟏𝟎
2𝒏 = 𝟒𝟎
𝒏 = 𝟐𝟎
∠𝑵 = (2𝒏 + 𝟏𝟎)°
∠𝑵 = 𝟐(𝟐𝟎) + 𝟏𝟎 °
∠𝑵 = 𝟒𝟎 + 𝟏𝟎 °
∠𝑁 = 50°

26. Example 4
∆𝑳𝑬𝑻 ≅ ∆𝑵𝑶𝑾, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒙.
30 cm
4x-2 cm
∠𝑳 ≅ 𝐿𝐸 ≅
∠𝑬 ≅ 𝐸𝑇 ≅
∠𝑻 ≅ 𝑇𝐿 ≅
∠𝑵
∠𝑶
∠𝑾
𝑵𝑶
𝑶𝑾
𝑾𝑵
Solve for x:
𝑳𝑬 ≅ 𝑵𝑶
𝐿𝐸 = 𝑁𝑂
3𝑥 − 5 = 70
3𝑥 = 70 + 5
3𝑥 = 75
Divide it both side by 3
𝒙 = 𝟐𝟓
𝑬𝑻 ≅ 𝑶𝑾
𝐸𝑇 = 𝑂𝑊
30 = 4𝑥 − 2
30 + 2 = 4𝑥
32 = 4𝑥
Divide it, both side by 4
X=8
L
E T
N
O W

27. Example 4
∆𝑳𝑬𝑻 ≅ ∆𝑵𝑶𝑾, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒙.
30 cm
4x-2 cm
∠𝑳 ≅ 𝐿𝐸 ≅
∠𝑬 ≅ 𝐸𝑇 ≅
∠𝑻 ≅ 𝑇𝐿 ≅
∠𝑵
∠𝑶
∠𝑾
𝑵𝑶
𝑶𝑾
𝑾𝑵
Solve for x:
𝑳𝑬 ≅ 𝑵𝑶
𝐿𝐸 = 𝑁𝑂
3𝑥 − 5 = 70
3𝑥 = 70 + 5
3𝑥 = 75
Divide it both side by three
𝒙 = 𝟐𝟓
𝑬𝑻 ≅ 𝑶𝑾
𝐸𝑇 = 𝑂𝑊
30 = 4𝑥 − 2
30 + 2 = 4𝑥
32 = 4𝑥
Divide it, both side by 4
X=8
𝑻𝑳 ≅ 𝑾𝑵
𝑻𝑳 = 𝑾𝑵
19 = 6𝑥 − 5
19 + 5 = 6𝑥
24 = 6𝑥
Divide it, both side by 6
𝒙 = 𝟒
L
E T
N
O W
N
O W

28. Activity Time!
∆𝐁𝐄𝐂 ≅ ∆𝑩𝑶𝑪, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒙.
CORRESPONDING
CONGRUENT ANGLES
CORRESPONDING
CONGRUENT SIDES
(2n + 5)°
35
45
100

29. Activity Time!
∆𝐑𝐈𝐄 ≅ ∆𝑹𝑳𝑬, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒙.
CORRESPONDING
CONGRUENT ANGLES
CORRESPONDING
CONGRUENT SIDES
70 cm

30. Assignment:
∆𝐌𝐎𝐀 ≅ ∆𝑨𝑹𝑬, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒏.

31. Activity Time!
∆𝐌𝐀𝐍 ≅ ∆𝑫𝑬𝑵, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒙.
CORRESPONDING
CONGRUENT ANGLES
CORRESPONDING
CONGRUENT SIDES
M
E
D
N
N
A
130°
20° x°

32. Activity:
∆𝐌𝐎𝐀 ≅ ∆𝑨𝑹𝑬, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒏.
R
E
A
M
A
O
70°
20°
50°
(2n + 10)°
CORRESPONDING
CONGRUENT ANGLES
CORRESPONDING
CONGRUENT SIDES

34. Assessment:
∆𝐌𝐎𝐀 ≅ ∆𝑨𝑹𝑬, 𝒔𝒐𝒍𝒗𝒆 𝒇𝒐𝒓 𝒂𝒏𝒈𝒍𝒆 𝒏, 𝒙 𝒂𝒏𝒅 𝒔𝒊𝒅𝒆 𝒙 .
R
E
A
M
A
O
75
50°
(2n + 10)°
CORRESPONDING
CONGRUENT ANGLES
CORRESPONDING
CONGRUENT SIDES
x
20 cm
7x - 3 cm
90 cm

35. Thank You.