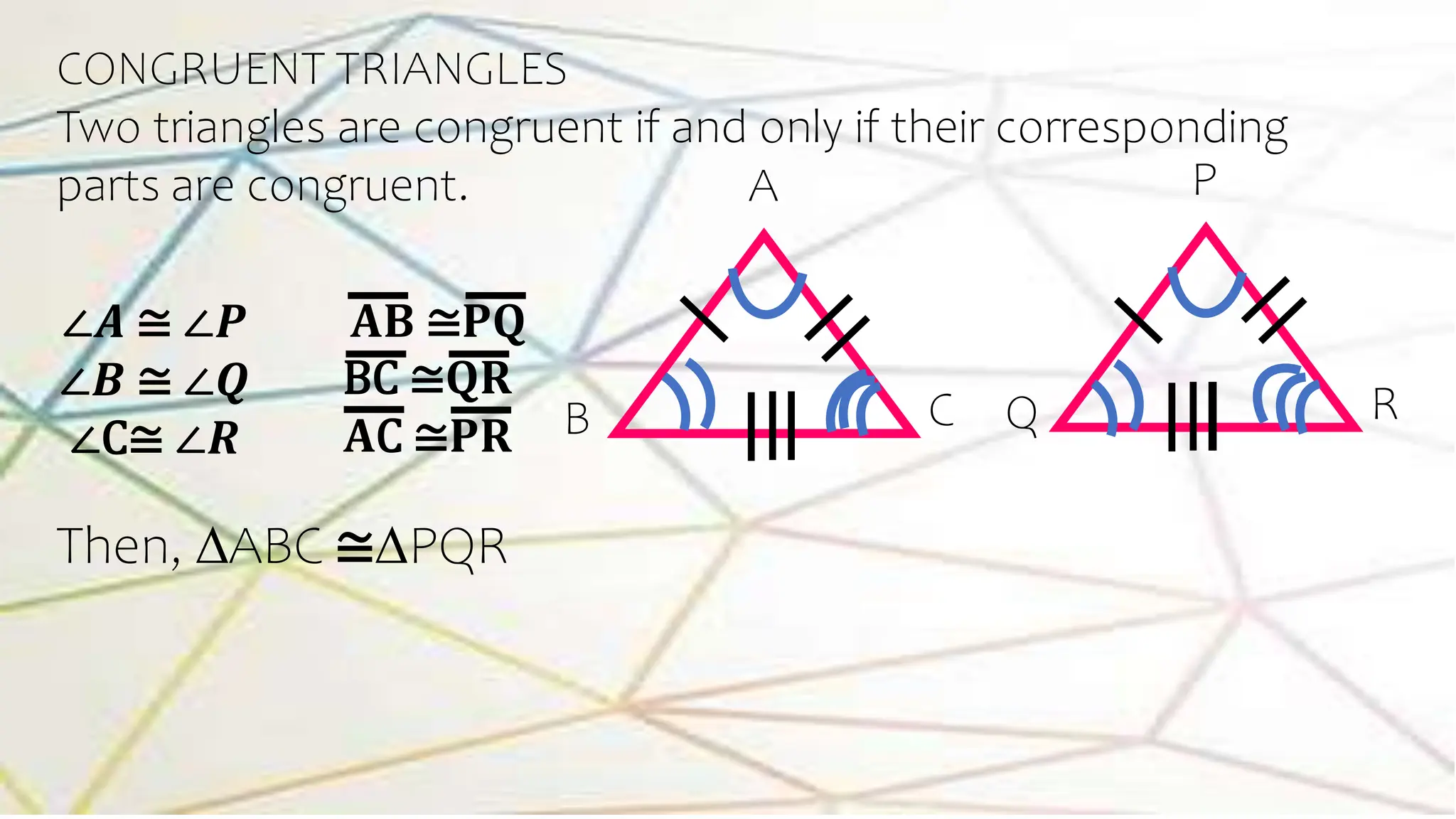
The document explains the concept of congruence in geometry, detailing how two figures can be congruent if they have the same shape and size, denoted by the symbol ≅. It highlights the significance of properties like reflexive, symmetric, and transitive in establishing congruence, along with examples involving triangles and their corresponding parts. Additionally, it emphasizes that for two polygons to be congruent, their vertices must match in a way that ensures all corresponding sides and angles are congruent.

1. If you slide the pink triangle to the
right, in which color will it fit in?

3. If you slide the green triangle to
the right, in which color will it fit in?

5. If you flip the blue triangle, in
which color will it fit in?

7. Means having the same shape and size,
and it is denoted by ≅. The top part of
the symbol,∼, is the sign for similarity
and indicates the same shape. The
bottom part symbol, = , is the sign of
equality and indicates the same size.

9. The idea of congruence always helps to
recognize congruent figures in the same
orientation. When two figures are
congruent, you may slide, flip, rotate the
figures until they overlap exactly.

10. The properties of equality as well as the properties of
congruence that follow from them are often used in doing
formal geometric proof.
REFLEXIVE PROPERTY OF
CONGRUENCE
SYMMETRIC PROPERTY
OF CONGRUENCE
TRANSITIVE PROPERTY OF
CONGRUENCE
∠𝑨 ≅ ∠𝑨
𝑨𝑩 ≅ 𝑨𝑩
If ∠𝑨 ≅ ∠𝑩, 𝒕𝒉𝒆𝒏
∠𝑩 ≅ ∠𝑨
If 𝑨𝑩 ≅ 𝑪𝑫, 𝒕𝒉𝒆𝒏
𝑪𝑫 ≅ 𝑨𝑩
If ∠𝑨 ≅ ∠𝑩, 𝒂𝒏𝒅 ∠𝑩 ≅ ∠𝑪 𝒕𝒉𝒆𝒏
∠𝑨 ≅ ∠𝑪
If 𝑨𝑩 ≅ 𝑪𝑫, 𝒂𝒏𝒅 𝑪𝑫 ≅ 𝑬𝑭 𝒕𝒉𝒆𝒏
𝑨𝑩 ≅ 𝑬𝑭

11. If ∆ABC slides over to the right to fit in ∆JKL, they will fit
exactly. However, they will fit exactly only if a proper pairing
of the vertices is made. In this case, the proper pairing will
have to be:
A to J or A ↔ J read as “ A corresponds to J.”
B to K or B ↔ K read as “ B corresponds to K.”
C to L or C ↔ L read as “ C corresponds to L.”
A
B C K
J
L
When the vertices are matched this way, ∠𝐴 𝑎𝑛 ∠𝐽 are corresponding
angles and AC and JL are corresponding sides.
Corresponding angles and corresponding sides are examples of
corresponding parts. Figures are congruent if all pairs of corresponding
sides and angles are congruent.

12. The correspondence among vertices can be used to name
the corresponding congruent sides and angles of the two
triangles.
∠𝑨 ≅ ∠𝑫
∠𝑩 ≅ ∠𝑬
∠𝑪 ≅ ∠𝑭
If two triangles are congruent, then their corresponding parts are also
congruent. (Corresponding Parts of Congruent Triangles are Congruent) or
CPCTC.
Two polygons are congruent if and only if their vertices can be matched
up so that their corresponding parts are congruent.
𝐀𝐁 ≅ 𝐃𝐄
BC ≅ 𝐄𝐅
𝐀C ≅ 𝐃𝐅

13. CONGRUENT TRIANGLES
Two triangles are congruent if and only if their corresponding
parts are congruent.
∠𝑨 ≅ ∠𝑷
∠𝑩 ≅ ∠𝑸
∠C≅ ∠𝑹
Then, ∆ABC ≅∆PQR
𝐀𝐁 ≅𝐏𝐐
BC ≅𝐐𝐑
𝐀C ≅𝐏𝐑
A
B C
P
Q R