First part of my NYU Tandon course "Numerical and Simulation Techniques in Finance"

Numerical & Simulation
Techniques in Finance
FRE 6251
Chapter I
Edward D. Weinberger, Ph.D, F.R.M.
Adjunct Assoc. Professor
NYU Tandon School of Engineering
edw@wpq-inc.com
Copyright 2018 Weinberger
Post-Quantitative, Inc.

THE PURPOSE OF
COMPUTING IS INSIGHT,
NOT NUMBERS…
--- R. W. Hamming

COURSE OBJECTIVES
•To familiarize students with
•what makes a “good” method
•some important methods
•EXCEL/VBA
•To teach the “informed use” of
numerical methods in packages

COURSE
ORGANIZATION
Grade based on
• Two algorithm implementations (50%
each)
• Required texts:
• Numerical Methods in C(++) by Frank Press, et. al.
(available free at http://www.nrbook.com/a/bookcpdf.php
• Options, Futures and Other Derivatives
`

TOPIC SCHEDULE
(Approximate!)
I. Root finding in 1 or more dim
II. Ordinary Differential Eqns.
(ODE’s)
III. Partial Differential Eqns. (PDE’s)
IV. Numerical Integration
V. Interpolation
VI. A Survey of Optimization

OUTLINE
Chapter I
• VBA survey for programmers
• “Machine numbers”
• 1 dim root finding methods
• bisection
• secant method
• Newton’s method
• Newton’s method in >1 dim
• ODE solvers

VBA for Programmers
• VBA NOT “industrial strength”,
unlike C++ (VBA not really OO)
• Visual Basic for Applications (VBA)
is macro language for all MS Office
• Built-in references to relevant
“objects”
• EXCEL/VBA has “Range”, “Cell”,
“Worksheet” objects (see HELP)

More VBA for
Programmers
• EXCEL functions accessible in VBA,
Applications.WorksheetFunction.min()
• “Immediate” window
• Integrated development environment
• “Record Macro” to get hints

“MACHINE NUMBERS” AS
SUBSETS OF R
• Integers represented in binary using 1
(“char”), 2 (“short”), 4 (“float”), or 8
(“long”) bytes
• Floating point numbers represented in
4 (“float”) or 8 (“double”) bytes
• Implications:
•Integer/floating point overflow
•Tests like (x == 0.25) may not work
•Cancellation (see example)

“MACHINE EPSILON”
• Smallest absolute value of non-zero
mantissa representable on machine
• Different for different machines and
different applications
• For EXCEL/VBA on my machine:
•1.19 x 10-7 for single precision
•9.31 x 10-10 for double precision

RELATIVE SPEED
ESTIMATION
• Want machine independent estimates
• Addition/Subtraction/branching fast
• Multiplication/Division slow
• Function calls slowest
• Use O(N ) notation

FIRST PROBLEM
Compute implied volatility of
European call option (e.g. one
dimensional root finding)

BISECTION METHOD
LO HIMID
If f(MID) ≥ 0
HI = MID
Else
LO = MID

SECANT METHOD
xn-2 xn-1xn
     
1
21
21
11



 








nn
nn
nnn
xx
xfxf
xfxx

NEWTON’S METHOD
xn-1 xn
xn-2
 
 










1
1
1
n
n
nn
xf
xf
xx

ROOT FINDER TRADE-
OFFS
METHOD ADVANTAGE DISADVANTAGE
Bisection Always converges Very slow (lots of fct evaluations)
Secant Fast (few fct evaluations)
Need not code separate
derivative
calculation
Can get lost
Newton Fastest Need code for derivative calculation
Can get lost
Brent Almost as fast as secant, but
doesn’t get lost.
Complex!

Desiderata
“Read user’s mind” regarding
what user wants, finding a
solution
• correctly and reliably (lever
expert knowledge, e.g. Brent)
• quickly and cheaply
• in a user friendly way,
consistent with how users think

THE STATE OF THE ART
• Numerical Libraries (Numerical
Recipes)
• Batch processing for numerical
calculation (GAMS)
• Interactive processing for numerical
calculation (MatLab)
• Symbolic calculation (Macsyma,
Maple, Mathematica, esp integrator)

THE STATE OF THE ART
• Numerical Integration of Block Diagrams
(SimuLink)
See also Wikipedia entry
http://en.wikipedia.org/wiki/
Comparison_of_numerical_
analysis_software

Types of Calculations
• Statistical Analysis
EXCEL, SAS, S+, R, GAMS, MatLab/Octave
• Matrix Manipulation
EXCEL, MatLab/Octave
• Optimization
EXCEL, MatLab/Octave, GAMS
• Differential Equations (ODE, PDE)
MatLab/OctaveCopyright 2018 Weinberger

Types of Calculations
• Special Functions
EXCEL (Normal Dist.), MatLab/Octave
• Fast Fourier Transform (FFT)
EXCEL, MatLab/Octave
• Root Finding
EXCEL (Solver), MatLab/Octave
• Numerical Integration
MatLab/OctaveCopyright 2018 Weinberger

NEWTON’S METHOD IN >1
DIMENSION
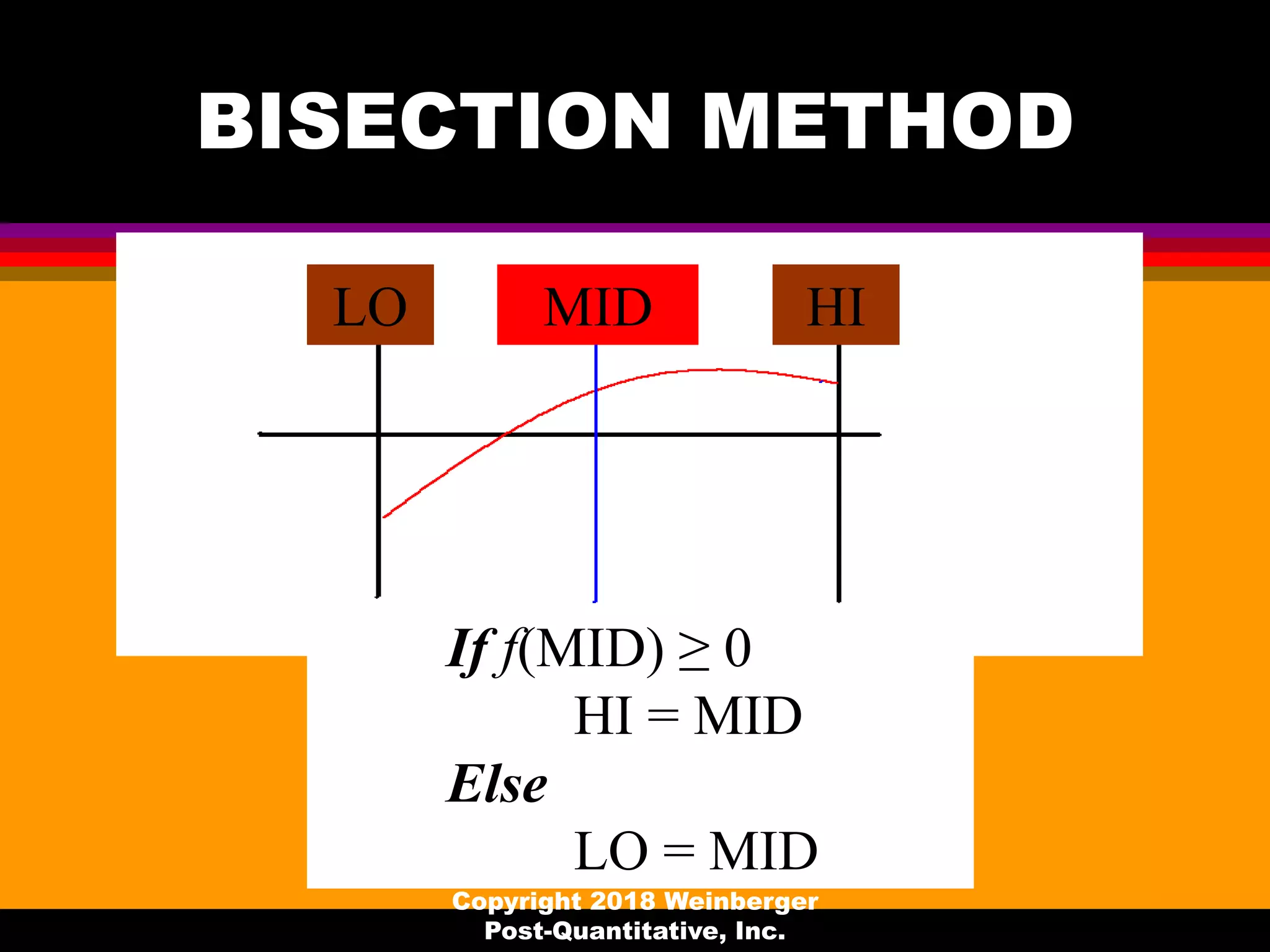
GOAL: Solve f (x) = 0, for “smooth” f by
iteration: Given xn, improve it to xn+1 = xn + δ
f (xn + δ) = f (xn) + J δ + O (|| δ ||2),
where
J = [∂ fi / ∂ xj ]

NEWTON’S METHOD IN >1
DIMENSION (cont)
Using f (xn + δ) = 0
0 ≈ f (xn) + J δ
so
- J -1 f (x) ≈ δ
and
xn = xn-1 + δ

SECOND PROBLEM
Compute numerical solution to
an ordinary differential
equation

HOW DO WE KNOW A
SOLUTION EXISTS?
ODE with no real solution:
12
2






x
dt
dx

ODE’S IN STANDARD
FORM
Almost any ODE or system of ODE’s can be written
in the form
dx1/dt = f1(x1, x2 … xN , t)
dxN /dt = fN (x1, x2 … xN , t)
}dx(t) /dt = f (x, t)

PICARD EXISTENCE
THEOREM
THEOREM: The initial value problem
dx/dt = f (x,t)
with initial condition x(0) = x0 has a unique real solution in the
appropriate region if f satisfies a “Lipschitz condition”, i.e.
|| f (y, t) - f (x, t) || ≤ const X || y - x ||
for all relevant t.

EULER’S METHOD
By definition,
     
        hohttxftxhtx
h
txhtx
dt
tdx
h





,
lim
0
xn+1 = xn+ h f (xn , tn)

EXAMPLE: SIMPLE
HARMONIC MOTION
d x1/dt = x2
d 2 x/dt2 = -4π2 k 2x
d x2/dt = -4π2 k2 x1
x1(t + h) = x1 (t) + x2(t) h
x2(t + h) = x2 (t) – 4π2 k 2 x1(t) h

EULER’S IMPLICIT
METHOD
In one dimension, use
x(t + h) = x(t) + f (x (t + h), t + h) h.
so
x(t + h) - f (x (t + h), t + h) h = x(t).
xn+1 = xn+ h f (xn+1 , tn+1)

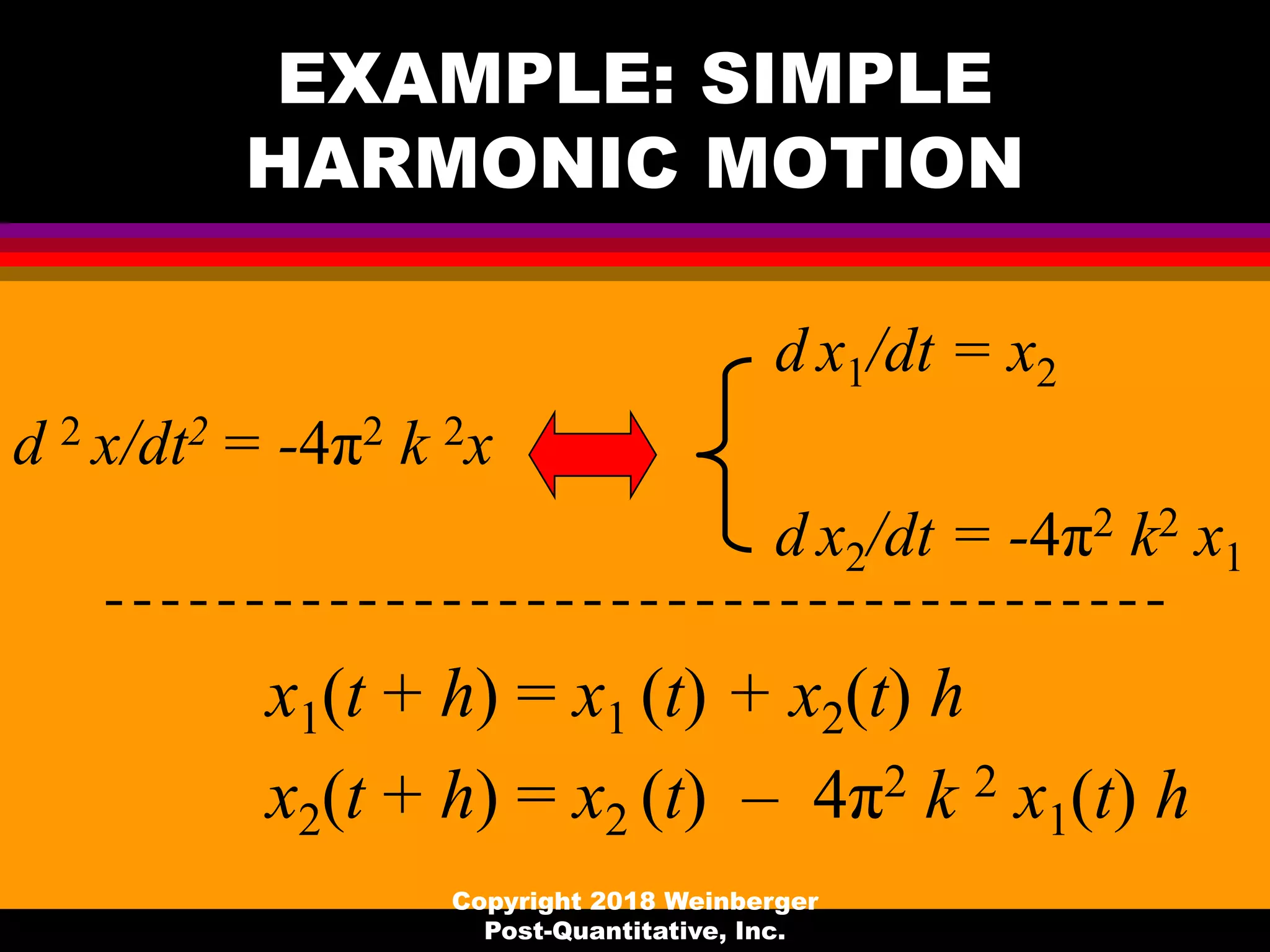
EXAMPLE: SIMPLE
HARMONIC MOTION
x1(t + h) – x2(t + h) h = x1 (t)
x2(t + h) + 4π2 k2 x1(t + h) h = x2 (t)
x1(t + h) = [x1(t) + x2(t) h] / [1 + 4π2 k2 h]
x2(t + h) = [- 4π2k2h x1(t) + x2(t)] / [1 + 4π2k2h]

STABILITY ANALYSIS:
EULER’S (EXPLICIT) METHOD
Consider: dx/dt = - ax, a > 0
x(t + h) = x(t)[1 - ah]
x(t + nh) = x(t)[1 - ah]n
so we must have |1 – ah| < 1, or h < 2/a for
convergence

STABILITY ANALYSIS:
EULER’S (IMPLICIT) METHOD
Consider: dx/dt = - ax
x(t + h) = x(t) - ah x(t + h)
x(t + h) = x(t) /[1 + ah]
x(t + nh) = x(t) /[1 + ah]n
Much better convergence properties!!

MIDPOINT METHOD
For any function g(t), Taylor series expansion is
     
     
     2
32
2
2
2
1
32
2
2
2
1
2
hO
dt
dg
h
htghtg
hOh
dt
gd
h
dt
dg
tghtg
hOh
dt
gd
h
dt
dg
tghtg
n
nn
nn
tt
nn
ttttnn
ttttnn








MIDPOINT METHOD
In the present case
   
 
    
        
        .,2/
But.2/,2/
so,2/,2/
2/2
2
2
1
3
2
hOhttxftxhtx
hOhhthtxftxhtx
hOhthtxf
h
txhtx





MIDPOINT METHOD
HENCE
xn +1 = xn + h f (xn + k1/2, tn + h/2) + O(h 3)
k1 = h f (xn , tn)
if stepsize = h
OR
xn +1 = xn -1 + 2h f (xn, tn) + O(h 3)
if stepsize = 2h

MIDPOINT METHOD
xn xn+ h
xn+ h/2
f(xn+ h/2, yn)

CONSISTENCY: NECESSARY
BUT NOT SUFFICIENT
A method is consistent if its order of
accuracy is at least 1, i.e. truncation error
is O(h2)
Explicit Euler, Implicit Euler, and the
Midpoint method are all consistent.

WHAT WE REALLY WANT IS
CONVERGENCE
A method is convergent if
Max | xj – x(tj) | 0
as h 0

MULTI-STEP METHODS
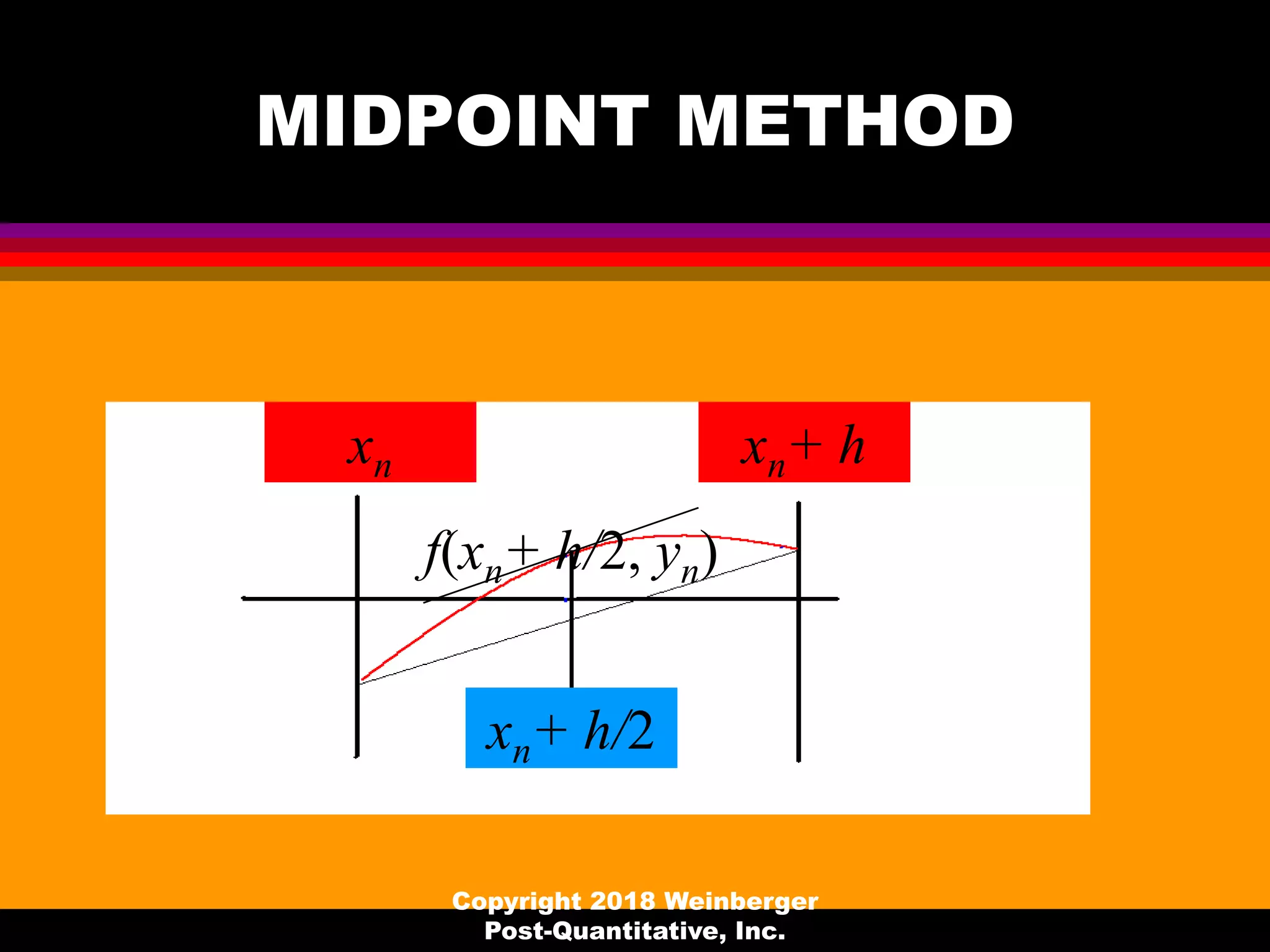
Why not generalize midpoint method to
xn+1 = a0 xn + a1 xn-1 + a2 xn-2 + …
+ h [b0 f(xn , tn) + b1 f(xn-1 , tn-1) + …]
as long as formula is consistent?

MULTI-STEP METHODS
Answer: Not always stable
xn+1 = -4 xn + 5xn-1 + h [4 f(xn , tn) + 2 f(xn-1 , tn-1)]
is unstable for any h!

DAHLQUIST EQIVALENCE
THEOREM
Theorem: A multi-step method for solving an ODE
is consistent and stable if and only if it is convergent
(stay tuned for more on this)

RUNGE KUTTA
(4th Order)
k1 = h f (xn , yn)
k2 = h f (xn + h/2, yn + k1/2)
k3 = h f (xn + h/2, yn + k2/2)
k4 = h f (xn + h, yn + k3)
yn +1 = yn + k1/ 6+ k2/ 3+ k3/ 3+ k4/ 6 + O(h5)

RUNGE KUTTA
Adaptive Step Size
x = True solution
xh = RK solution with step size h
x2h = RK solution with step size 2h
x(t + 2h) = xh(t + 2h) + 2h 5φ + O(h6)
x(t + 2h) = x2h(t + 2h) + (2h) 5φ + O(h6)

RUNGE KUTTA
Adaptive Step Size
Δ =x2h(t + 2h) - xh(t + 2h) = 30h 5φ + O(h6)
If |Δ| > Tol1 then
replace h with h/2
else if |Δ| < Tol2 then
replace h with 2h
end if

SUMMARY
Chapter I
• VBA highlights
• “Machine numbers”
• 1 dim root finding methods
• bisection
• secant method
• Newton’s method
• Newton’s method in >1 dim
• ODE solvers

First part of my NYU Tandon course "Numerical and Simulation Techniques in Finance"

More Related Content

What's hot

Similar to First part of my NYU Tandon course "Numerical and Simulation Techniques in Finance"

Recently uploaded

First part of my NYU Tandon course "Numerical and Simulation Techniques in Finance"