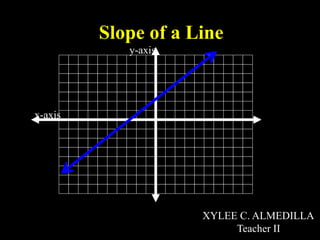
This document discusses the concept of slope of a line. It begins by defining key terms like the x-axis, y-axis, and slope. It then shows how to calculate slope using the rise over run formula. Several examples are worked out step-by-step, such as finding the slope between points (-3,6) and (5,2). Real-world applications of slope are discussed. Students are expected to understand how to describe trends using slope, calculate slope, and relate slope to real life.

1. Slope of a Line
x-axis
y-axis
XYLEE C. ALMEDILLA
Teacher II

2. At the end of the discussion the
students are expected to:
1) Describe the trends of the graph by
the value of the slope.
2) Find the slope of a line; and
3) Relate the lesson in real-life setting.

3. REVIEW
x-axis
y-axis
ORIGIN
Quadrant I
Quadrant II
Quadrant III Quadrant IV

4. Plot the Points!
1. A(3,-1) and B(3,-5)
2. A(-5,1) and B(-1,1)
3. A(-5,-1) and B(-1,4)
4. A(1,4) and B(3,2)

5. Sample Situation:
When I was a child, my sister and I walked
2 kilometers each day for school. Part of that
walk included a very steep hill. One rainy day,
we were walking down the slippery hill and my
sister slipped and fell. Her school books came
out of her hands and slid all the way down the
hill and into a storm sewer. When we arrived at
school, we told our teacher about our ordeal. To
this day, I remember that very steep hill.

6. Slope
Slope - refers to the steepness of a line. It also
describes the direction of a line.

7. Guard against 0 in
the denominator
Slope
If x1  x2, the slope of the line
through the distinct points P1(x1, y1)
and P2(x2, y2) is:
1
2
1
2
x
x
y
y
x
in
change
y
in
change
run
rise
slope





m

8. x-axis
y-axis
Find the slope between (0,0) and (6, 4)
Rise
Run
4 2
3
= =
(0,0)
(6, 4)
6

9. x-axis
y-axis
Find the slope between (-3, 6) and (5, 2)
Rise
Run
-4
8
-1
2
= =
(-3, 6)
(5, 2)

10. Calculate the slope between (-3, 6) and (5, 2)
1
2
1
2
x
x
y
y
m



)
3
-
(
)
5
(
)
6
(
)
2
(



m
8
4
-

2
1
-

x1 y1 x2 y2
We use the letter m
to represent slope
m

11. Find the Slopes
(5, -2)
(11, 2)
(3, 9)
1
2
1
2
x
x
y
y
m



3
11
9
2
1



m
5
11
)
2
-
(
2
2



m
3
5
9
2
-
3



m
8
7
-

Yellow
3
2

Blue
Red
2
11
-


12. Find the Slopes
(5, -2)
(11, 2)
(3, 9)
1
2
1
2
x
x
y
y
m



3
11
9
2
1



m
Yellow
5
11
)
2
-
(
2
2



m
Blue
3
5
9
2
-
3



m
Red
8
7
-

3
2

2
11
-


13. Rise Over Run!
Find the following:
1. Rise = 30
2. Run = 10
3. Slope = 3

14. Find the following:
1. Rise = 2
2. Run = 2
3. Slope = 1

15. Find the slope of a line!
1. A(3,-1) and B(3,-5)
2. A(-5,1) and B(-1,1)
3. A(-5,-1) and B(-1,4)
4. A(1,4) and B(3,2)

16. Ratio of my Changes!
Group 1: A(0,2) and B(1,8)
Group 2: A(-1,8) and B(-2,-5)
Group 3: A(-11,5) and B(4,5)
Group 4: A(4,7) and B(9,7)

17. Group 1: A(0,2) and B(1,8)
.
1
2
1
2
x
x
y
y
m



x1 y1 x2 y2
1 - 0 1
m = =
8 - 2 6
= 6

18. Group 2: A(-1,8) and B(-2,-5)
.
1
2
1
2
x
x
y
y
m



x1 y1 x2 y2
-2 - (-1) -1
m = =
-5 - 8 -13
= 13
-2 + 1
-5 + -8
=

19. Group 3: A(-11,5) and B(4,5)
.
1
2
1
2
x
x
y
y
m



x1 y1 x2 y2
4 - (-11) 15
m = =
5 - 5 0
= 0
4 + 11
0
=

20. Group 4: A(5,15) and B(9,12)
.
1
2
1
2
x
x
y
y
m



x1 y1 x2 y2
9 - 5
m =
12 - 15
4
-3
=

28. Evaluate!
Direction: Find the slope of a line given
two points then graph the points in the
Cartesian Plane. Show your solutions.
1. A(-2,-4) and B(0,3)
2. A(0,3) and B(2,1)
3. A(1,1) and B(5,1)
4. A(2,4) and B(2,1)

29. Assignment!
Make a short essay, a poster or a poem
about the importance of the slope of a
line.