This document contains solutions to various financial management assignment questions. It includes calculations to determine the monthly savings required to accumulate $60,000 over 5 years, NPV calculations at different discount rates, computing future values of investments and superannuation, calculating monthly pension amounts, real vs nominal interest rates, effects of changing cash reserve ratios, risk-return tradeoffs of different investments, imputation credits, monthly/annual returns of stocks, standard deviation and beta calculations using CAPM model, and constructing a portfolio with expected return. Formulas and step-by-step workings are provided for all calculations.

1. 1
Financial Management Assignment
Questions with Answers
Question-1-a
Formula used to solve the problem:
Solution of the problem:
Amount needed -60000
Years 5
Moths 60
Rateper month 0.33%
Savings required per
month $904.99
Thus, in order to save $60,000 in five years, a sum of $904.99 would be required to
be deposited each month.
Question-1-b-i
Discount
rate 10%
Year Cash flows PVF@10%
Present
value
0 (22.00) 1.000 (22.00)
1 1.80 0.909 1.64
2 3.00 0.826 2.48
3 6.50 0.751 4.88
4 8.40 0.683 5.74
5 12.30 0.621 7.64
NPV 0.37

2. 2
As the net present value of the project as calculated above in this financial
management assignment is $0.37 million. Hence, the NPV is positive therefore the
project is acceptable.
Question-1-b-ii
Yes, the answer would change. Now, the increase in discount rate from 10% to 15%
leads to negative NPV which implies that the project is not financial worthy.
Discount
rate 15%
Year Cash flows PVF@10%
Present
value
0 (22.00) 1.000 (22.00)
1 1.80 0.870 1.57
2 3.00 0.756 2.27
3 6.50 0.658 4.27
4 8.40 0.572 4.80
5 12.30 0.497 6.12
NPV (2.97)
Question-1-c-i
The value of Brant’s financial assets when he retires at age 67 is computed as
below:
Brant is now 34 years and he retires at 67 so the time period is 33 years
Value of portfolio after 33 years:
C0 = 47,000 (present value of portfolio)
R = 7%
N = 33 years
= 47,000*(1+7%)^33
= 47,000*9.325
= 438,275

3. 3
Value of superannuation after 34 years:
Value of superannuation:
Present value 78000
Monthly contribution 1000
Time- months 396
Rate-monthly 0.67%
Value of
superannuation $3,017,140.93
Total value of financial assets of Brant will be $3,893,706 ($438,275+$3,017,140)
Question-1-c-ii
The calculation of monthly pension amount for Brant is given as below:
Where,
R = rate of investment (5% pa or 0.42% monthly)
PVA = present value of annuity ($3,893,706-120,000 set aside
= 3,773,706)
N = time period (18 years, counted from 67 to 85, or 216
months)
Monthly pension annuity:
Total amount available $3,773,706.00
Time- months 216
rate-monthly 0.42%
Annuity $26,530.43
Question-2-a-1
The bank quotes 4% interest rate for the loan. This is the nominal interest rate not
yet adjusted for the effects of inflation.

4. 4
Question-2-a-2
The real interest rate identifies in this financial management assignment signifies
that rate of interest which has been adjusted for the effect of inflation on the other
hand; the notional interest rate is the rate that has not been adjusted for inflation
effect. Thus, the real interest shows the actual earnings of the banker in the form of
interest income received on the extended loan facility (McAndrews, 2015).
Question-2-a-3
The annual inflation rate in Australia is 1.60%.
Notional rate of interest is 4%
Real interest rate will be = 4%-1.60%
= 3.40% p.a.
Question-2-a-4
Yes, it is possible that the real interest rate becomes equal to the notional interest
rate. This situation can arise only when the inflation is zero in the economy.
Question-2-b
The cash reserve ratio is the regulatory requirement that all banks and financers
being regulated by the Reserves Bank of Australia must comply with. The Reserve
Bank of Australia uses the cash reserve ratio as the tool of monetary policy. When
the reserve ratio is increased, the bankers or financers would have to maintain more
reserve funds and hence it reduces their liquidity. On the other hand, when the RBA
reduces the cash reserve ratio, this increases the liquidity of the banks and
financiers. The increase in liquidity gives more power to the banks to lend money
and thus, it also affects the loan interest rates. The loan interest rates could be
lowered down by the bankers which ultimately provide benefits to the borrowers.
Hence, if RBA reduces the cash reserve rate by 0.25%, it will increase availability of
funds in the hands of the banks. Now, the supply of money would increase which
would result in reduction in the cost of borrowing for the borrowers (Becker, Fang, &
Wang, 2016).
Question-3-a-i
Due to less risk-taking capacity, Bradley is considering investing in Bank guaranteed
investment which provides return of 1%. The marginal tax rate applied on the income
of Bradley is 32.5% and additional 2% medicare levy is also applied. The prevailing
inflation is 2.5%. Thus, it can be seen in this financial management assignment that
the rate of inflation is higher than the after tax return that Bradley would receive from
the investment in bank guaranteed investment. Supporting computations are shown
as below:

5. 5
Amount invested (assumed) 100,000.00
Return @1% 1,000.00
Less: Tax @ 32.5% 325.00
Less: Medicare levy @2% 20.00
Return after tax 655.00
Dollar value of investment after 1 year
(100000/(1+2.5%) 97,560.98
Diminution in the value (100000-
97560.98) 2,439.02
The after tax return on the investment is only $655 whereas the diminution in the
value of investment amount over the period of 1 year is $2,439.02. Thus, it is clearly
seen that Bradley is not able to preserve the dollar value of its investment.
Question-3-a-ii
Every investment involves risk. Some may involve lower risk and some may be with
higher risk. The return and risk run in parallel. If the investor wants higher returns, it
would come with only higher risk. Therefore, there forms a simple principle that
higher the risk, higher would be the returns or vice a versa. It is essential for Bradley
to understand that taking high risk is not always a bad strategy because it would land
to high returns at the same time. The biggest advantage of taking high risk in
investing is that the investor can widen the range of profits. The low risk investments
narrow down the profit range would result in shrinkage in net returns from the
investment (Chari, David, Duru, & Zhao, 2019).
Question-3-b
Imputation credit (franking credit) discussed in this Financial Management
assignment means the credit given to the shareholders on the part of the taxes paid
by the company on profits so that the dividends distributed by the company could be
saved from double taxation. The profits earned by the company are taxed in the
hands of the company and then it distributes dividend to the shareholders which is
again taxed in the hands of the investor. Therefore, in order to provide relief to the
investor, the dividend imputation credit system was brought into force. Now, the
investor receiving dividend could claim credit of the taxes paid by the company and
reduce their overall tax liability (Dixon & Nassios, 2016).
The investors of Australia would receive fully franked dividend which entitles the
investor to take credit of the taxes already paid by the company on the amount of
dividend declared. However, a foreign investor would not be able to utilize the

6. 6
franking credit and hence the tax liability in that case would be higher as compared
to the local Australian investor.
Question-3-c-i
Date Open Close
Monthly
Holding
period
returns
($)
Monthly
Holding
period
returns
(%)
Jul-17 3.79 4.14
Aug-17 4.15 5.04 0.90 21.74%
Sep-17 5.10 5.86 0.82 16.27%
Oct-17 5.92 7.62 1.76 30.03%
Nov-17 7.34 7.59 (0.03) -0.39%
Dec-17 7.60 7.37 (0.22) -2.90%
Jan-18 7.40 8.29 0.92 12.48%
Feb-18 8.32 12.23 3.94 47.53%
Mar-18 12.21 11.46 (0.77) -6.30%
Apr-18 10.96 11.31 (0.15) -1.31%
May-18 11.36 9.93 (1.38) -12.20%
Jun-18 9.70 10.52 0.59 5.94%
Question-3-c-ii
Average Monthly Holding period returns (%):
Average = (21.74%+16.27%+30.03%+-0.39%+-
2.90%+12.48%+47.53%+-6.30%+-1.31%+-
12.20%+5.94%)/ 11
= 10.08%

7. 7
Question-3-c-iii
Annual holding period return
$ 6.38 (10.52-4.14)
% 154.11%
(10.52-
4.14)/4.14
Question-3-d-i
The calculation for monthly holding period return is shown as below:
(Dividend + (latest price – previous price)) / Previous price) * 100
Date Open Close
Monthly Holding
period returns (%)
Jul-17 5,764.00 5,773.90
Aug-17 5,773.90 5,776.30 0.04%
Sep-17 5,776.30 5,744.90 -0.54%
Oct-17 5,744.90 5,976.40 4.03%
Nov-17 5,976.40 6,057.20 1.35%
Dec-17 6,057.20 6,167.30 1.82%
Jan-18 6,167.30 6,146.50 -0.34%
Feb-18 6,146.50 6,117.30 -0.48%
Mar-18 6,117.30 5,868.90 -4.06%
Apr-18 5,868.90 6,071.60 3.45%
May-18 6,071.60 6,123.50 0.85%
Jun-18 6,123.50 6,289.70 2.71%

8. 8
Question-3-d-ii
Average of monthly holding period returns is given as below:
= (0.04%+-0.54%+4.03%+1.35%+1.82%+-0.34%+-0.48%+-
4.60%+3.45%+0.85%+2.71%)/ 11
= 0.80%
Question-3-d-iii
iii) Annual holding period
return
% 8.93%
(6289.70-
5773.90)/5773.90
Question-3-d-iv
Line graph showing monthly returns of A2M and MKT is presented as below:
Figure 1: Monthly Returns of A2M and MKT

9. 9
Question-3-d-v
The calculation of standard deviation (risk) for A2M and MKT is given below in this
Financial Management assignment:
Standard deviation (A2M)
X x- (x- )^2
Aug-17 21.74% 11.66% 1.36%
Sep-17 16.27% 6.19% 0.38%
Oct-17 30.03% 19.95% 3.98%
Nov-17 -0.39% -10.48% 1.10%
Dec-17 -2.90% -12.98% 1.68%
Jan-18 12.48% 2.40% 0.06%
Feb-18 47.53% 37.45% 14.02%
Mar-18 -6.30% -16.38% 2.68%
Apr-18 -1.31% -11.39% 1.30%
May-18 -12.20% -22.28% 4.97%
Jun-18 5.94% -4.14% 0.17%
10.08% Total 31.70%
17.80%

10. 10
Standard deviation (MKT)
X x- (x- )^2
Aug-17 0.04% -0.76% 0.01%
Sep-17 -0.54% -1.35% 0.02%
Oct-17 4.03% 3.23% 0.10%
Nov-17 1.35% 0.55% 0.00%
Dec-17 1.82% 1.01% 0.01%
Jan-18 -0.34% -1.14% 0.01%
Feb-18 -0.48% -1.28% 0.02%
Mar-18 -4.06% -4.86% 0.24%
Apr-18 3.45% 2.65% 0.07%
May-18 0.85% 0.05% 0.00%
Jun-18 2.71% 1.91% 0.04%
0.80% Total 0.51%
2.27%
Question-3-d-vi
The beta value of A2M is 1.04 times which reflect the sensitivity of the stock relative
to the overall market. Beta is also known as the measure of systematic risk. The
interpretation of beta value is given in terms of times. For instance, A2M has beta of
1.04 times which implies that if market moves up side by 10%, the stock of A2M will
move up side by 10.40% and if market goes down by 10%, the stock of A2M will be
down by 10.40%. The higher the beta of the stock higher will be the risk and vice a
versa. Beta value of 1.04 indicates that the A2M is moderately risky stock
(Bollerslev, Li, & Todorov, 2016).

11. 11
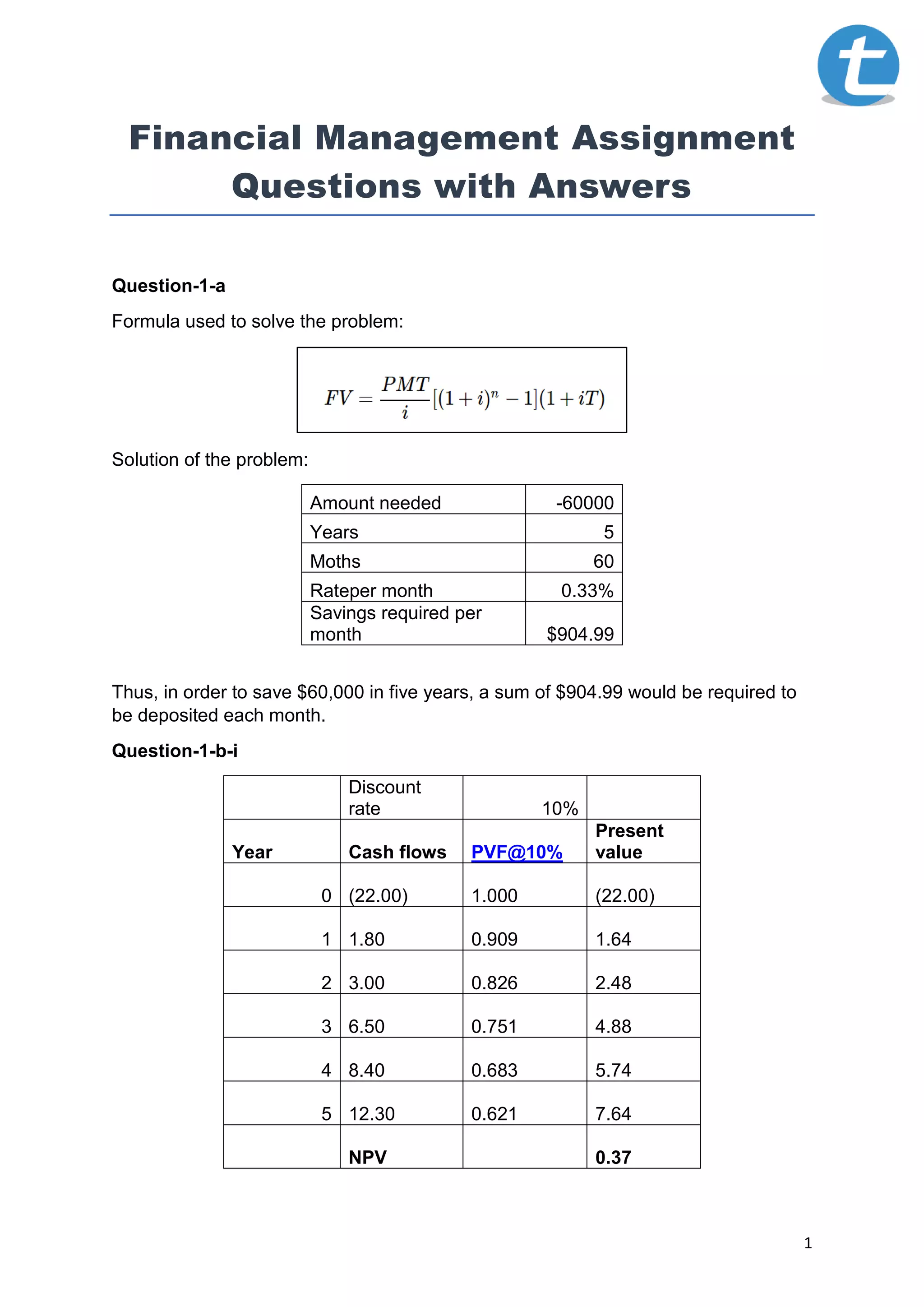
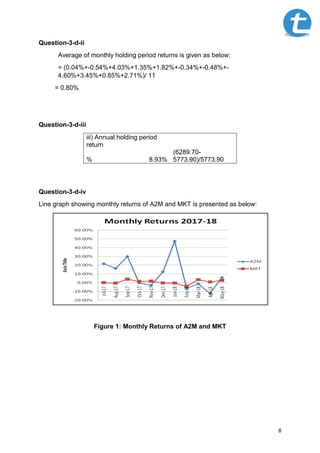
Question-3-d-vii
The calculation of expected return of A2M applying the CAPM model is given as
below:
Where,
Ra = Expected return
Rrf = Risk free rate
Ba = Beta value of stock
Rm = Market return
Market return 9.55%
Risk free rate 2.29%
Beta 1.04
CAPM
[2.29%+(9.55%-
2.29%)*1.04] 9.84%
Question-3-d-viii
The SML chart for A2M is given below:
Figure 2: SML A2M

12. 12
Question-3-d-ix
The recreated chart with actual returns of A2M and MKT is presented as below:
Figure 3: SML chart
Question-3-d-x
The portfolio using 40% and 60% weights of A2M and MKT respectively is given as
below:
Construct
portfolio
A2M MKT
Weight 40% 60%
Return 10.08% 0.80%
Beta 1.04 1
Expected return of the portfolio is the weighted average return of the securities
comprising of the portfolio (Bollerslev, Li, & Todorov, 2016):
= 10.08%*40%+0.80%*60%
= 4.52%
The portfolio beta is the weighted average beta of the securities comprising of the
portfolio:
= 1.04*40%+1*60%
= 1.02