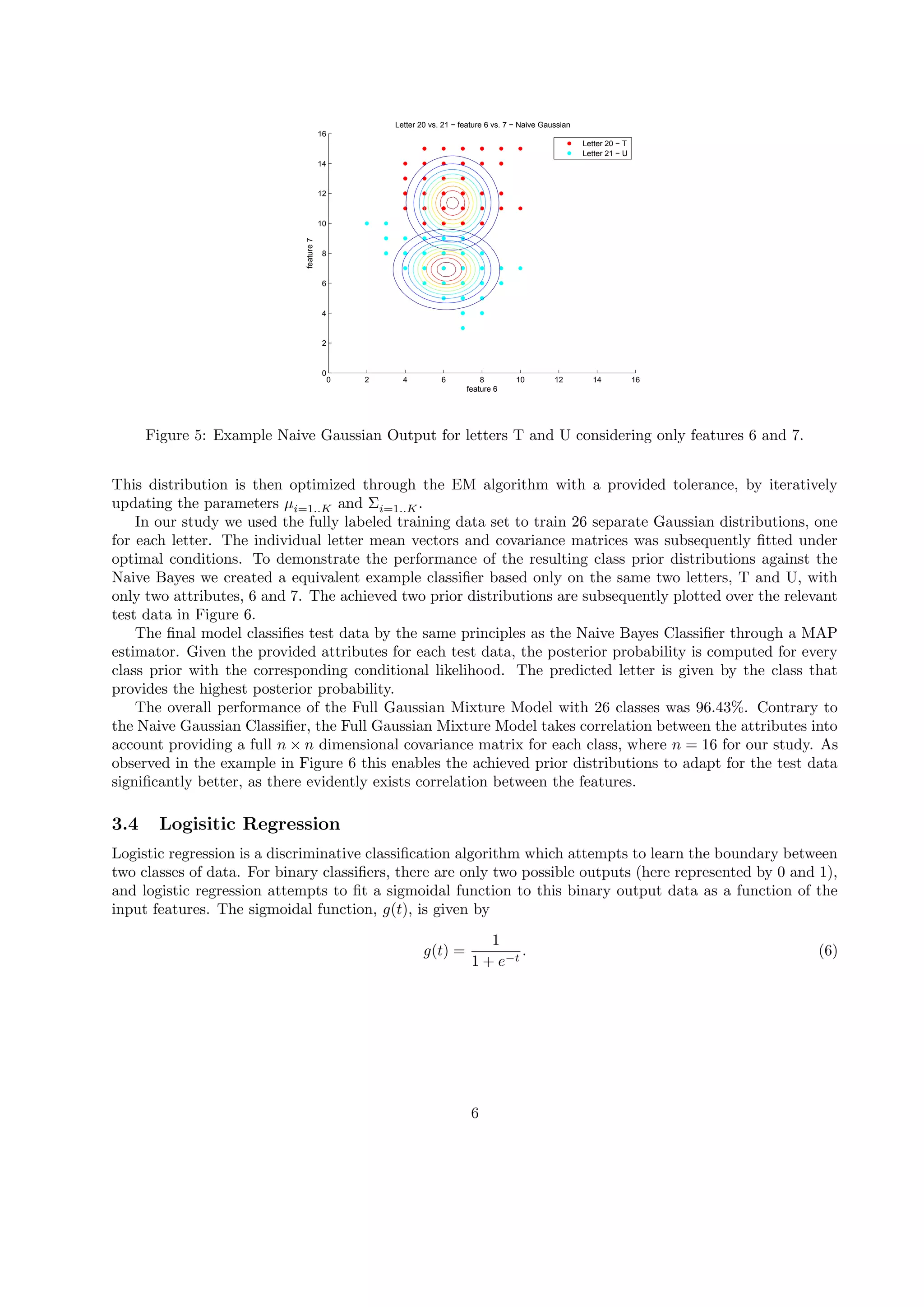
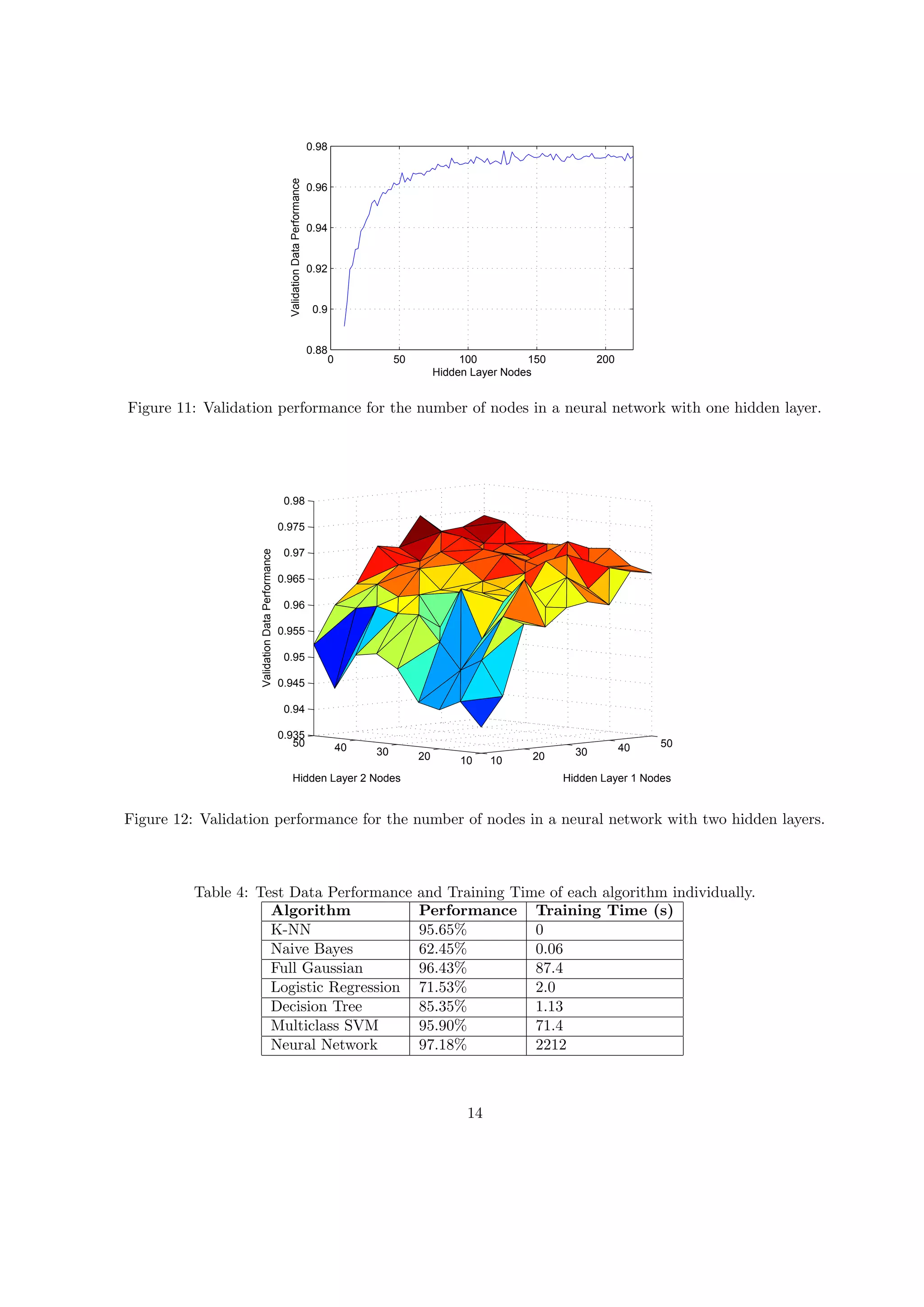
- The document describes a study that used various machine learning algorithms to classify images of letters based on 16 extracted features. - The best performing algorithm was the Gaussian Mixture Model, which achieved 96.43% accuracy by modeling each letter as a Gaussian distribution and accounting for correlations between features. - The k-Nearest Neighbors algorithm achieved 95.65% accuracy when using only the single nearest neighbor for classification, while the Naive Bayes classifier achieved only 62.45% due to its strong independence assumptions.

1. 18-752 Project
Letter Recognition
Andrew Fox, Fridtjof Melle
May 5, 2014
1 Introduction
For our 18-752 Estimation, Detection, Identification course project, we engaged in a numerical study testing
various statistical analysis and machine learning algorithms in an attempt to classify typed letters based on
predetermined features. Our goal with this study was in the broadest sense to classify and discriminate images
by letter, by comparing the attainment of various modeling algorithms while assessing their strengths and
weaknesses. We use these experiences to achieve the highest possible performance, with a hybrid realization
of these algorithms, and further assess their influence and individual performance. Motivations for proceeding
with the analysis of this data set include the fact that letter and word recognition remain an active field of
study, and is also a task for which computers significantly lag behind humans in performance.
2 Data Set
The data set used for this study was created by David J. Slate [1] with the objective of identifying a processed
array of distorted letter images as one of the 26 capital letters in the English alphabet.
For the purpose of generating the data set an algorithm was created whose output would be an English
capital letter uniformly drawn from the letters of alphabet, randomly selected among 20 different fonts.
The fonts included five stroke styles (Simplex, Duplex, Triplex, Complex and Gothic) and six letter styles
(Block, Script, Italic, English, Italian and German). To further complicate the generated images, each letter
underwent a random distortion process including vertical and horizontal warping, linear magnification and
changes to the aspect ratio. Examples of the resulting images from the data set are shown in Figure 1.
The algorithm produced 20,000 unique letter images. Each image was converted into 16 primitive nu-
merical attributes, each values as a normalized 4-bit number with an integer value ranged from 0 through
15. The attributes used to construct the 16 features are detailed in Table 1. An example of the final data
points extracted from the data set is displayed in Figure 2.
For the purpose of this study we divided the data set of 20,000 letter images into two sets. To develop
the different models we allocated the first 16,000 letters as training data. The training data was divided
into 13,600 training images and 2,400 validation images for algorithms which required validation processes.
The remaining 4,000 letter images for used for testing. We further developed a z-score of the features and
replaced the letter labels with respective respective integers such that,
A = 1, B = 2, .., Z = 26. (1)
This label replacement was done for programming convenience. It should be noted that numerical closeness
between two letters does not represent letters that are close are similar to each other. This should be kept in
mind when using models that use regression analysis for classification. The concept of being close numerically
does not represent closeness between classes. Algorithms may favor numerically close letters, although there
is no real comparable basis for this consideration. Efforts were made in this project to use the algorithms in
a way which avoided this issue.
1

2. Figure 1: Example letter images generated for the data set
Table 1: Attribute information for each feature representation
Feature 1 Horizontal position of minimum-size letter-enclosing box
Feature 2 Vertical position of minimum-size letter-enclosing box
Feature 3 Width of minimum-size letter-enclosing box
Feature 4 Height of minimum-size letter-enclosing box
Feature 5 Total number of pixels making up letter
Feature 6 Mean horizontal position of pixels relative to center of box
Feature 7 Mean vertical position of pixels relative to center of box
Feature 8 Mean-squared horizontal position of pixels relative to center of box
Feature 9 Mean-squared vertical position of pixels relative to center of box
Feature 10 Mean correlation of horizontal and vertical means
Feature 11 Mean vertical position correlation with horizontal variance
Feature 12 Mean horizontal position correlation with vertical variance
Feature 13 Mean number of horizontal letter edge pixels measuring left to right
Feature 14 Sum of respective vertical positions of edge pixels measured
Feature 15 Mean number of vertical letter edge pixels measuring bottom to top
Feature 16 Sum of respective horizontal positions of edge pixels measured
2

3. X,4,9,5,6,5,7,6,3,5,6,6,9,2,8,8,8
H,3,3,4,1,2,8,7,5,6,7,6,8,5,8,3,7
L,2,3,2,4,1,0,1,5,6,0,0,6,0,8,0,8
H,3,5,5,4,3,7,8,3,6,10,6,8,3,8,3,8
E,2,3,3,2,2,7,7,5,7,7,6,8,2,8,5,10
Y,5,10,6,7,6,9,6,6,4,7,8,7,6,9,8,3
H,8,12,8,6,4,9,8,4,5,8,4,5,6,9,5,9
Q,5,10,5,5,4,9,6,5,6,10,6,7,4,8,9,9
M,6,7,9,5,7,4,7,3,5,10,10,11,8,6,3,7
E,4,8,5,6,4,7,7,4,8,11,8,9,2,9,5,7
N,6,11,8,8,9,5,8,3,4,8,8,9,7,9,5,4
Y,8,10,8,7,4,3,10,3,7,11,12,6,1,11,3,5
W,4,8,5,6,3,6,8,4,1,7,8,8,8,9,0,8
O,6,7,8,6,6,6,6,5,6,8,5,8,3,6,5,6
N,4,4,4,6,2,7,7,14,2,5,6,8,6,8,0,8
H,4,8,5,6,5,7,10,8,5,8,5,6,3,6,7,11
O,4,7,5,5,3,8,7,8,5,10,6,8,3,8,3,8
N,4,8,5,6,4,7,7,9,4,6,4,6,3,7,3,8
H,4,9,5,6,2,7,6,15,1,7,7,8,3,8,0,8
Figure 2: Example Data extracted from data set
3 Methodology
The following subsections summarize the different algorithms that we used for letter classification and how
they were applied to our problem. Generally the models had 16 input dimensions, the features, and had an
output representing either the chosen letter or a decision on the comparison between letters. Understanding
of these algorithms was assisted by [2].
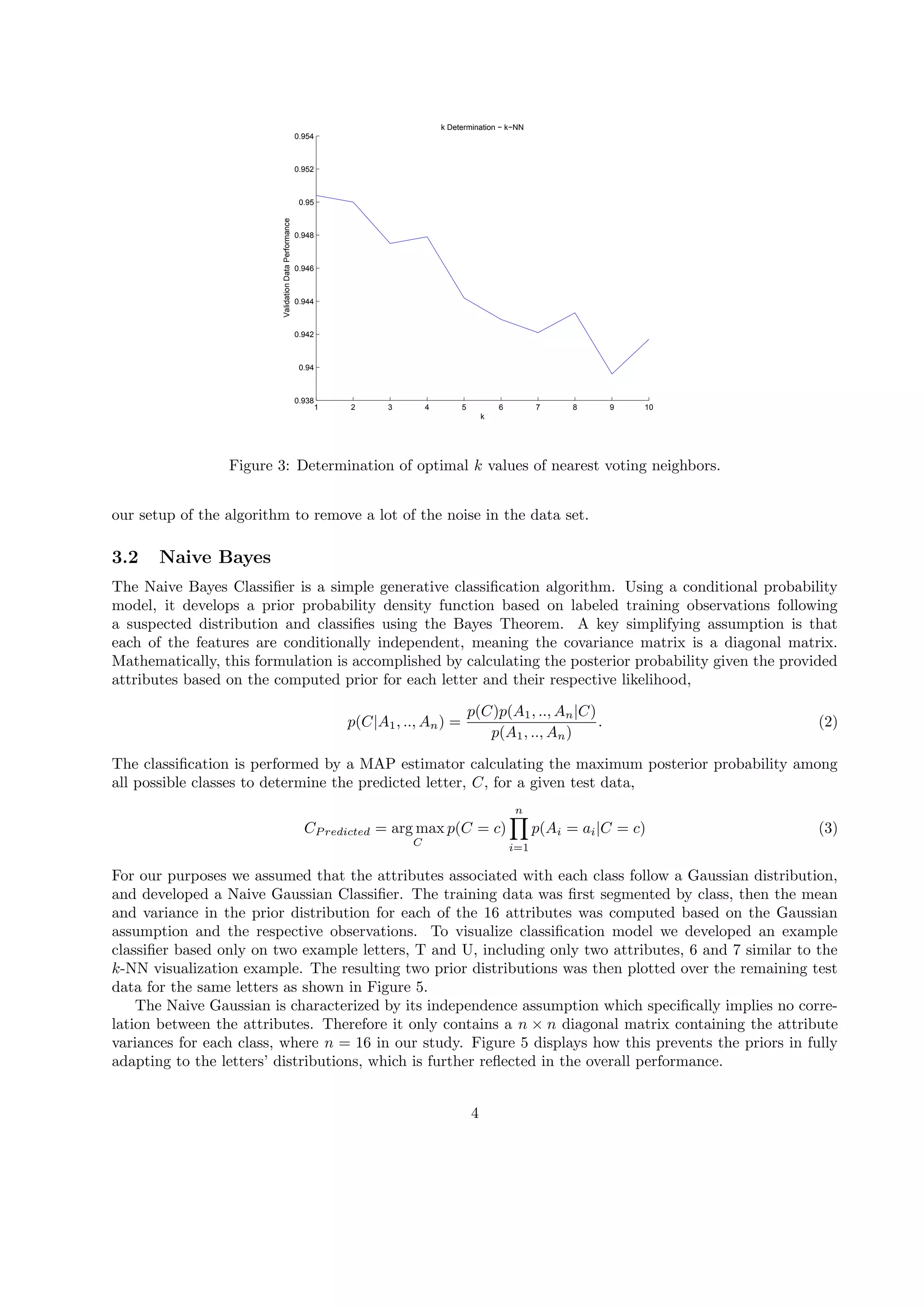
3.1 k-Nearest Neighbors
The k-Nearest Neighbors algorithm is a discriminative classifier that uses a deterministic association to
distinguish the data points. The output label for a test letter is a class membership determined by a
majority vote of its k closest neighbors in the feature space by Euclidean distance. The performance is
optimized by determining what value k of nearest neighbors which performs best on the validation data. A
k too large includes too much distant and irrelevant data, while a k too small risks misclassifications due to
noise.
The graph of validation performance with respect to different k values is shown in Figure 3. The best
result was achieved with letting only one nearest neighbor vote, k = 1. This result is line with the fact that
the features are normalized to 4-bit values which limits the potential possibilities in the feature space and
leads to a lot of the data set thereby overlapping. Classifying a given test image based on only the majority
of letters having the same feature value may therefore be sufficient.
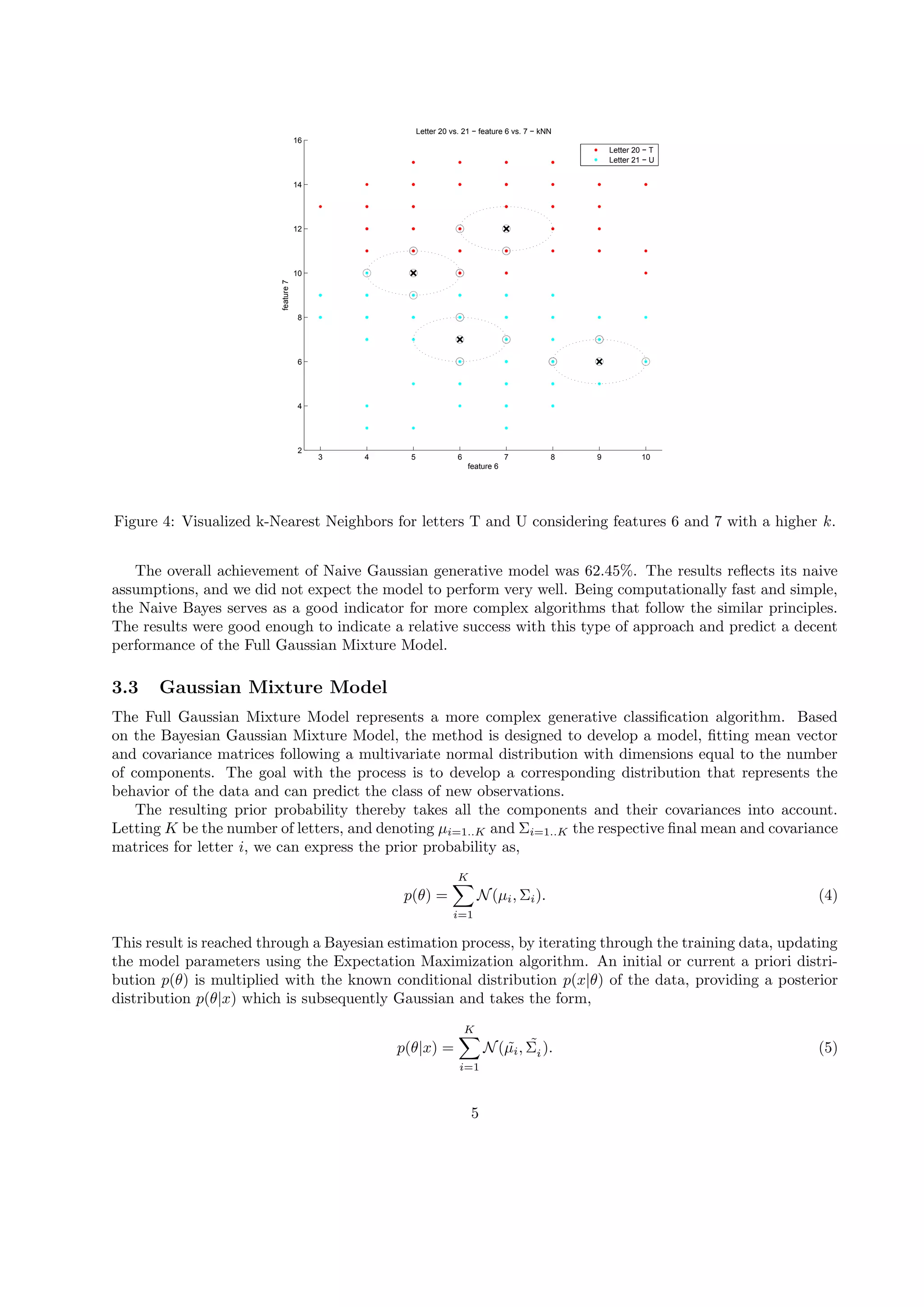
To visualize the classification process we extracted two letter examples, T and U from the training data
set, with two of their features (6 and 7) in Figure 4. On this data we added two test letters of each class
and classified them by a higher number of neighbors to visualize the voting process. As our k determination
process concluded with k = 1 for optimal results, our output will in reality only take in account the letters
having obtained the same value for the majority vote. It should be noted that this classification appears to
perform relatively poorly. That is due to the fact that we only used 2 features for simple visualization. The
full 16 dimensional feature space with all 26 letters would be impossible to illustrate.
The overall performance of the k-Nearest Neighbor Algorithm on the test data was 95.65%. This over
adequate achievement can be due to the sparsely ranged values of the attributes which enables us through
3

4. 1 2 3 4 5 6 7 8 9 10
0.938
0.94
0.942
0.944
0.946
0.948
0.95
0.952
0.954
k Determination − k−NN
k
ValidationDataPerformance
Figure 3: Determination of optimal k values of nearest voting neighbors.
our setup of the algorithm to remove a lot of the noise in the data set.
3.2 Naive Bayes
The Naive Bayes Classifier is a simple generative classification algorithm. Using a conditional probability
model, it develops a prior probability density function based on labeled training observations following
a suspected distribution and classifies using the Bayes Theorem. A key simplifying assumption is that
each of the features are conditionally independent, meaning the covariance matrix is a diagonal matrix.
Mathematically, this formulation is accomplished by calculating the posterior probability given the provided
attributes based on the computed prior for each letter and their respective likelihood,
p(C|A1, .., An) =
p(C)p(A1, .., An|C)
p(A1, .., An)
. (2)
The classification is performed by a MAP estimator calculating the maximum posterior probability among
all possible classes to determine the predicted letter, C, for a given test data,
CP redicted = arg max
C
p(C = c)
n∏
i=1
p(Ai = ai|C = c) (3)
For our purposes we assumed that the attributes associated with each class follow a Gaussian distribution,
and developed a Naive Gaussian Classifier. The training data was first segmented by class, then the mean
and variance in the prior distribution for each of the 16 attributes was computed based on the Gaussian
assumption and the respective observations. To visualize classification model we developed an example
classifier based only on two example letters, T and U, including only two attributes, 6 and 7 similar to the
k-NN visualization example. The resulting two prior distributions was then plotted over the remaining test
data for the same letters as shown in Figure 5.
The Naive Gaussian is characterized by its independence assumption which specifically implies no corre-
lation between the attributes. Therefore it only contains a n × n diagonal matrix containing the attribute
variances for each class, where n = 16 in our study. Figure 5 displays how this prevents the priors in fully
adapting to the letters’ distributions, which is further reflected in the overall performance.
4

5. 3 4 5 6 7 8 9 10
2
4
6
8
10
12
14
16
feature 6
feature7
Letter 20 vs. 21 − feature 6 vs. 7 − kNN
Letter 20 − T
Letter 21 − U
Figure 4: Visualized k-Nearest Neighbors for letters T and U considering features 6 and 7 with a higher k.
The overall achievement of Naive Gaussian generative model was 62.45%. The results reflects its naive
assumptions, and we did not expect the model to perform very well. Being computationally fast and simple,
the Naive Bayes serves as a good indicator for more complex algorithms that follow the similar principles.
The results were good enough to indicate a relative success with this type of approach and predict a decent
performance of the Full Gaussian Mixture Model.
3.3 Gaussian Mixture Model
The Full Gaussian Mixture Model represents a more complex generative classification algorithm. Based
on the Bayesian Gaussian Mixture Model, the method is designed to develop a model, fitting mean vector
and covariance matrices following a multivariate normal distribution with dimensions equal to the number
of components. The goal with the process is to develop a corresponding distribution that represents the
behavior of the data and can predict the class of new observations.
The resulting prior probability thereby takes all the components and their covariances into account.
Letting K be the number of letters, and denoting µi=1..K and Σi=1..K the respective final mean and covariance
matrices for letter i, we can express the prior probability as,
p(θ) =
K∑
i=1
N(µi, Σi). (4)
This result is reached through a Bayesian estimation process, by iterating through the training data, updating
the model parameters using the Expectation Maximization algorithm. An initial or current a priori distri-
bution p(θ) is multiplied with the known conditional distribution p(x|θ) of the data, providing a posterior
distribution p(θ|x) which is subsequently Gaussian and takes the form,
p(θ|x) =
K∑
i=1
N( ˜µi, ˜Σi). (5)
5

6. 0 2 4 6 8 10 12 14 16
0
2
4
6
8
10
12
14
16
feature 6
feature7
Letter 20 vs. 21 − feature 6 vs. 7 − Naive Gaussian
Letter 20 − T
Letter 21 − U
Figure 5: Example Naive Gaussian Output for letters T and U considering only features 6 and 7.
This distribution is then optimized through the EM algorithm with a provided tolerance, by iteratively
updating the parameters µi=1..K and Σi=1..K.
In our study we used the fully labeled training data set to train 26 separate Gaussian distributions, one
for each letter. The individual letter mean vectors and covariance matrices was subsequently fitted under
optimal conditions. To demonstrate the performance of the resulting class prior distributions against the
Naive Bayes we created a equivalent example classifier based only on the same two letters, T and U, with
only two attributes, 6 and 7. The achieved two prior distributions are subsequently plotted over the relevant
test data in Figure 6.
The final model classifies test data by the same principles as the Naive Bayes Classifier through a MAP
estimator. Given the provided attributes for each test data, the posterior probability is computed for every
class prior with the corresponding conditional likelihood. The predicted letter is given by the class that
provides the highest posterior probability.
The overall performance of the Full Gaussian Mixture Model with 26 classes was 96.43%. Contrary to
the Naive Gaussian Classifier, the Full Gaussian Mixture Model takes correlation between the attributes into
account providing a full n × n dimensional covariance matrix for each class, where n = 16 for our study. As
observed in the example in Figure 6 this enables the achieved prior distributions to adapt for the test data
significantly better, as there evidently exists correlation between the features.
3.4 Logisitic Regression
Logistic regression is a discriminative classification algorithm which attempts to learn the boundary between
two classes of data. For binary classifiers, there are only two possible outputs (here represented by 0 and 1),
and logistic regression attempts to fit a sigmoidal function to this binary output data as a function of the
input features. The sigmoidal function, g(t), is given by
g(t) =
1
1 + e−t
. (6)
6

7. 0 2 4 6 8 10 12 14 16
0
2
4
6
8
10
12
14
16
feature 6
feature7
Letter 20 vs. 21 − feature 6 vs. 7 − Full Gaussian
Letter 20 − T
Letter 21 − U
Figure 6: Example Full Gaussian Mixture Output for letters T and U considering only features 6 and 7.
An example of the sigmoidal function is shown in Figure 7. Since the range of the sigmoidal function is
[0, 1],we can use it to represent the a posteriori probability p(θ|x) for the two classes as,
p(θ = 0|x) = g(wT
x) =
1
1 + e−wT x
, (7)
p(θ = 1|x) = 1 − g(wT
x) =
e−wT
x
1 + e−wT x
. (8)
The mathematical objective of using Logistic Regression as a binary classifier is to determine the vector w.
This is determined using the log-likelihood function. Given n labeled data points, {(X1, θ1), . . . , (Xn, θn)},
the log-likelihood function, l(x) is given by,
l(x) =
n∑
i=1
θi ln(1 − g(wT
xi)) + (1 − θi) ln(g(wT
xi)) (9)
=
n∑
i=1
θiwT
xi − ln(1 + ewT
xi
) (10)
We can differentiate this log-likelihood with respect to w, equate to zero to find the maximum, and solve for
the maximizing value of w using gradient descent.
However logistic regression is a binary classifier and the Letter Recognition data set has 26 classes. To
account for this we create 26 different binary classifiers, each comparing an individual letter (denoted class
1) to all the remaining letters (denoted class 0). The determined letter corresponds to the maximum value of
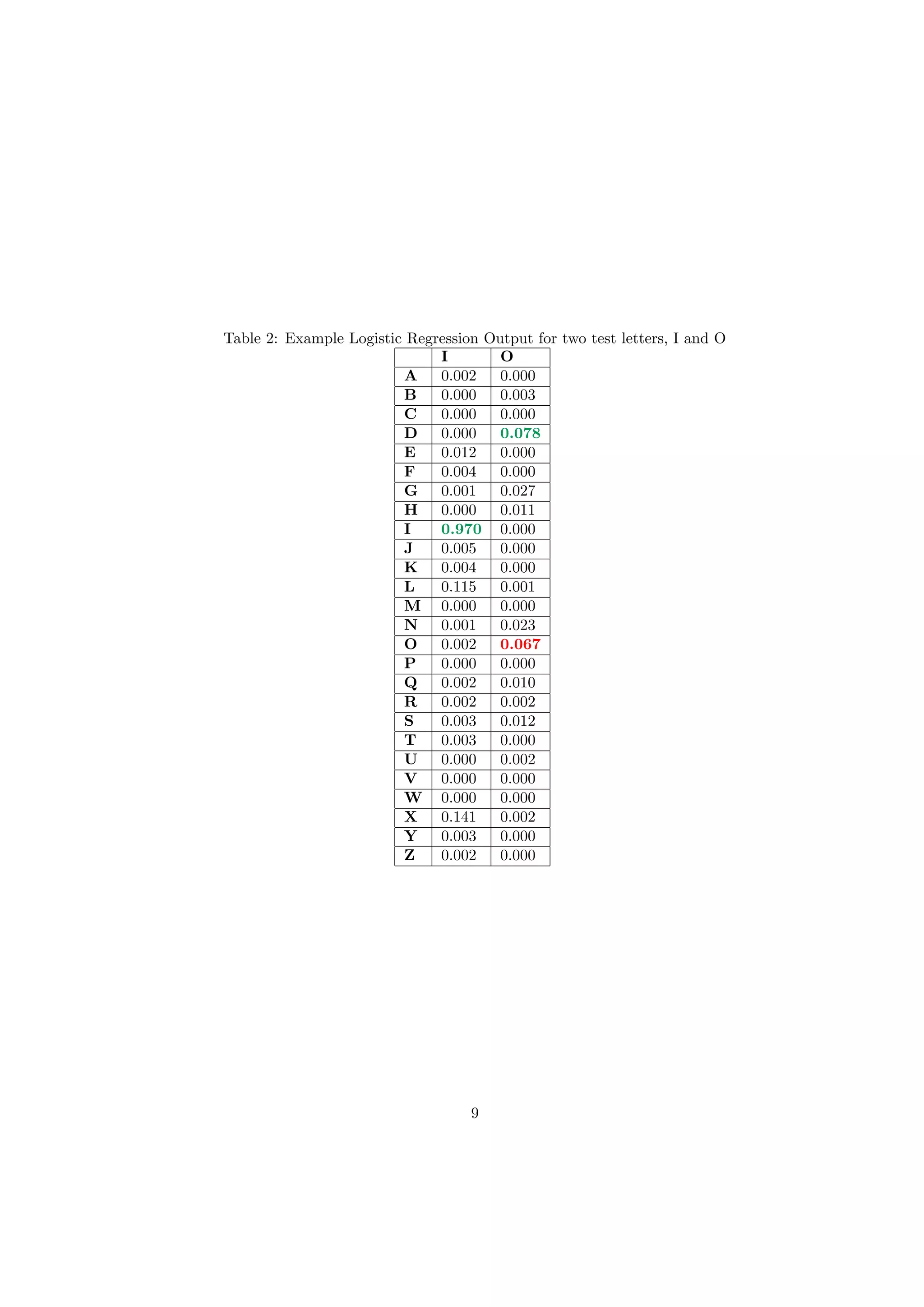
the output of each of the logistic regression functions. An example of the output for two test letter examples,
I and O is shown in Table 2. The letter I is correctly classified with the logistic regression outputting a value
close to 1 for I and close to 0 for every other letter. However for the given test letter O, the features result
in an output close to 0 for every logistic regression output and the letter is misclassified as a D.
The overall classification performance of the logistic regression algorithm on the test data was 71.53%.
One of the weaknesses of the algorithm is that the 26 models for each letter are derived independently and
the output values are therefore not directly comparable. Some letters may be further away from the rest
of the letters than others and therefore the boundaries for different models and the area of change in the
resulting sigmoidal function from 0 to 1 will vary in terms of its width. Therefore output values from some
7

8. −10 −5 0 5 10
0
0.2
0.4
0.6
0.8
1
t
g(t)
Sigmoidal Function
Figure 7: Graph of the Sigmoidal Function, g(t) = 1
1+e−t
of the logistic regression functions may be artificially high or low and could cause problems when being
compared across the 26 models. Additionally the logistic regression model is not good at finding multiple
boundaries. The sigmoidal function increases from 0 to 1 only once. Therefore if the 1-class data happens
to fall in the middle of the x spectrum with 0-class data on either side, the sigmoidal function will have
difficulties in capturing the characteristics of the boundary and classifying the data.
3.5 Decision Tree
Decision trees are an extremely intuitive way to make classification decisions as they they are essentially a
series of if-then-else questions one poses on the feature set until a classification determination is made. An
example of a three-class decision tree with two features is shown in Figure 8. Classification decisions are
made by beginning at the root node of the tree. One proceeds along the leaves of the tree at each node by
making a binary decision on a single feature using a threshold. For example at the root node, if x1 > a then
the tree proceeds to the right to make the classification determination, and if x1 ≤ a then the tree proceeds
to the left.
These binary decisions effectively split the feature space into n-dimensional hypercubes, where n is the
dimension of the feature space (16 in this study). This means that decision trees are effective at making
classification decisions when the data can be split along linear boundaries of only one variable, and also if
the output fits into multiple isolated clusters in the feature space. Intuitively, this then seems like it would
be very effective for the type of data given in this project. The features are 4-bit integers, non-continuous,
which allows for very natural boundary lines between different features.
In order to construct the decision tree one must determine what features to split the data on at each
node. This is done according to the feature which maximizes the information gain given the remaining data
set. We first introduce the concept of entropy, H(X), of a random variable which is effectively a measure of
the amount of randomness of the random variable,
H(X) = −
∑
i
P(xi) log2 P(xi), (11)
where xi is the set of possible outputs of the distribution. The conditional entropy is given by,
H(θ|X) = −
∑
i
∑
j
P(xi, θj) log2 P(θj|xi). (12)
We define the information gain I(θ, X) as,
I(θ, X) = H(θ) − H(θ|X). (13)
8

9. Table 2: Example Logistic Regression Output for two test letters, I and O
I O
A 0.002 0.000
B 0.000 0.003
C 0.000 0.000
D 0.000 0.078
E 0.012 0.000
F 0.004 0.000
G 0.001 0.027
H 0.000 0.011
I 0.970 0.000
J 0.005 0.000
K 0.004 0.000
L 0.115 0.001
M 0.000 0.000
N 0.001 0.023
O 0.002 0.067
P 0.000 0.000
Q 0.002 0.010
R 0.002 0.002
S 0.003 0.012
T 0.003 0.000
U 0.000 0.002
V 0.000 0.000
W 0.000 0.000
X 0.141 0.002
Y 0.003 0.000
Z 0.002 0.000
9

10. Figure 8: Example three-class decision tree using two features.
21 21
21 20
21 21 20
21
20 21
x2 < 9.5
x2 < 6.5 x1 < 3.5
x1 < 5.5 x2 < 10.5
x1 < 7.5 x1 < 4.5
x2 < 7.5
x1 < 6.5
x2 >= 9.5
x2 >= 6.5 x1 >= 3.5
x1 >= 5.5 x2 >= 10.5
x1 >= 7.5 x1 >= 4.5
x2 >= 7.5
x1 >= 6.5
Figure 9: Example decision tree for letters T and U using features 6 (labeled x1) and 7 (labeled x2).
The decision tree is made in a greedy manner, constructing a node at each stage that maximizes the
information gain. Intuitively, the information gain equation is the amount of randomness of the entire set
of outputs minus the amount of randomness of the output conditioned on a specific feature. If knowing a
value of the feature deterministically determines the output then the conditional entropy is zero and the
information gain is maximized. This would then be a good feature to construct the node with since the
output would then be known and the construction of the tree along that branch is completed.
Decision trees can be prone to overfitting through. As long as for any combination of features there is
only a single output, a tree can be constructed to correctly classify every training data. This situation needs
to be avoided. Therefore validation data is used to prune the decision tree to the point where the information
gane on the test data is above a threshold.
The overall performance of the decision tree on the test data was 85.35%. The entire tree would be
difficult to show due to its size, however as an example the decision tree for the letters T and U for features
6 and 7 (same as in previous sections) is shown in Figure 9.
10

11. 3.6 Multiclass Support Vector Machine
A Support Vector Machine (SVM) is a discriminative binary regression classifier used to find the boundary
between two classes of data. This is useful since it is often only the boundary that is of any consideration,
not the distribution of the data in entire classes. An example SVM is shown in Figure 10. Mathematically,
the goal of the SVM is to maximize the boundary between the data in class +1 and the data in class −1.
This is done by determining a vector w such that the classifier, ϕ(x), works as
ϕ(x) =
{
+1 , if sgn(wT
x) ≥ 0
−1 , if sgn(wT
x) < 0
. (14)
The margin between the data is equal to 2
||w|| . Therefore we can solve for w by attempting to minimize wT
w.
However we need to consider the case where the two classes are non-separable as shown in Figure 10. In this
case no linear boundary exists that can perfectly separate the two classes. So we add to our cost function a
penalty C times the distance ϵ that a data point is from its respective boundary plane, equal to zero if it is
on the correct side. Therefore the value w is determined as
argmin
w
1
2
wT
w +
n∑
i=1
Cϵi. (15)
This is a quadratic programming problem that can be solved easier in the dual formulation of the Lagrange
multipliers on the constraints classifying each point to it’s respective side of the boundary and that ϵi ≥ 0 ∀i.
This dual formulation is the following:
argmin
α
∑
i
αi−
1
2
∑
i,j
αiαjθiθjxixj (16)
∑
i
αiθi = 0 (17)
αi ≥ 0, ∀i (18)
w =
∑
i
αixiθi (19)
However this is only for a linear boundary in the SVM. We can extend the SVM to non-linear boundaries
using the kernel trick. Note that the minimization is a function of the dot product between xi and xj.
By replacing this dot product with another inner product, K(xi, xj), we can map the data to a higher
dimensional feature space and create a non-linear boundary line. For this analysis we use a radial basis
function
K(xi, xj) = exp
(
−
(xi − xj)T
(xi − xj)
2σ2
)
. (20)
The SVM is a two-class classifier so we need to extend it to be able to handle the 26 classes required
for this project. To do this we created
(26
2
)
SVMs. These SVMs do one-on-one comparisons between each
letter. The classification results for each letter are summed and the letter that is classified the most in the(26
2
)
SVMs is chosen as the final letter for classification.
The test performance of the multiclass SVM was 95.75%. The results for the same two letters chosen in
the logistic regression are shown for the multiclass SVM in Table 3. Each row represents the number of times
that letter was chosen in the
(26
2
)
SVMs. Note that in this case both the letters were correctly classified.
The results in this table may be slightly deceiving as there are a number of letters with very close values to
the one ultimately chosen. However this does not imply that the test letter resembles those letters closely
(although it still may). There are
(26
2
)
SVMs and one letter must be chosen in each of those classifiers, even
when comparing letters that the test letter is not remotely close to. That may seem to increase some of the
totals beyond what one would intuitively expect, however it is merely a result of the fact that the sum of
the column must equal
(26
2
)
and that each letter must have a result between 0 and 25.
11

12. Table 3: Example Multiclass Support Vector Machine Output for two test letters, I and O
I O
A 3 3
B 1 11
C 6 20
D 11 23
E 3 6
F 15 9
G 10 21
H 19 20
I 25 0
J 12 5
K 21 13
L 7 4
M 23 17
N 17 19
O 3 25
P 21 18
Q 18 24
R 9 14
S 21 18
T 10 8
U 12 12
V 3 2
W 16 9
X 10 8
Y 23 12
Z 6 4
-1 plane
+1 plane
jkε ε
Figure 10: Example Support Vector Machine with boundaries [3].
12

13. 3.7 Neural Network
The Neural Network is the final algorithm used to classify the letter data. Neural networks are generally
able to obtain extremely high accuracy, however at the expense of being extremely unintuitive, difficult to
track, and requiring a long training time. Neural networks consist of multiple layers of nodes, where the
output of each node in a layer serves as an input to every node in the succeeding layer. Every node in the
output layer executes a weighted linear summation of all its inputs, while each node in the inner (hidden)
layers executes a sigmoidal function on its inputs. These sigmoidal functions in the hidden layer nodes are
known as the activation functions.
Unlike the logistic regression which only determines one vector w to perform the classification, neural
networks require a determination of the w vector for every node. This is done by error backpropagation.
The high-level mathematical objective is to minimize the mean-square error between the predicted and true
output values. This mean square error function is then differentiated with respect to each w to determine
the values to minimize the MSE. This is done using gradient descent. We first randomize all w values and
determine the resulting error at each output j,
δj = θj − g(wT
vj), (21)
where vj is the vector of inputs into output node j. We can then propagate the effect of the error backwards
from node j to node i in the previous layer as
∆j,i = wiδj(1 − gj)gj. (22)
The (1 − g)g terms is a result of differentiating the sigmoidal function. This allows us to update all w values
from node i to node k as
wk,i = wk,i + λ
n∑
j=1
∆j,igj,i(1 − gj,i)xj,k. (23)
For our purposes we created 26 different neural networks, one for each letter comparing the letter to the
rest of the training data set, where the desired output from each network was 1 if the letter corresponded to
that particular network, or 0 otherwise. Each network had 16 input nodes (the features) and one output node.
We trained the neural network with varying amounts of nodes and hidden layers and tested the networks
using validation data to determine the appropriate number of nodes and layers. The validation performance
for one hidden layer is shown in Figure 11 and for two hidden layers in Figure 12. For one hidden layer,
the validation performance flatlined at approximately 0.974, however for the final network we chose to use
two hidden layers with 35 and 50 nodes respectively due to the fact that the validation performance almost
matches and the training time was hours shorter. All 26 of the neural networks were of identical size. Note
that this could have been another parameter to vary however it would require testing many more neural
networks. As is, the neural network still performed the best of any of the algorithms, having a test data
performance value of 97.18%.
3.8 Individual Algorithm Results
Table 4 summarizes the performance of each model individually as well as showing the resulting training times
for each algorithm. The Neural Network achieves the best performance, however takes orders of magnitude
more training time than the other algorithms. Due to the size of the test data set, and the fact that for
most of the algorithms the test phase is executing a series of set calculations, the test time is negligible and
comparable for each of the algorithms.
3.9 Hybrid Models
We created hybrid models of the various individual algorithms to attempt to increase the test performance
results. Each algorithm has weaknesses and misclassifications that were discussed in their respective sections,
13

14. 0 50 100 150 200
0.88
0.9
0.92
0.94
0.96
0.98
Hidden Layer Nodes
ValidationDataPerformance
Figure 11: Validation performance for the number of nodes in a neural network with one hidden layer.
10 20 30 40 50
1020304050
0.935
0.94
0.945
0.95
0.955
0.96
0.965
0.97
0.975
0.98
Hidden Layer 1 NodesHidden Layer 2 Nodes
ValidationDataPerformance
Figure 12: Validation performance for the number of nodes in a neural network with two hidden layers.
Table 4: Test Data Performance and Training Time of each algorithm individually.
Algorithm Performance Training Time (s)
K-NN 95.65% 0
Naive Bayes 62.45% 0.06
Full Gaussian 96.43% 87.4
Logistic Regression 71.53% 2.0
Decision Tree 85.35% 1.13
Multiclass SVM 95.90% 71.4
Neural Network 97.18% 2212
14

15. so the hope is that by combining algorithms that the strengths of some of the algorithms will be able to
overcome the weaknesses of others and therefore increase the overall performance.
The hybrid models are created using a voting scheme between the algorithms. Each individual algorithm
submits a 26-column vector corresponding to the amount that the algorithm is voting for each letter. There
are two weighting schemes. The first weighting scheme weights each algorithm equally, so that the sum of
the vote vector for each algorithm equals 1. The second weighting scheme weights each algorithm according
to their performance so that the sum of the vote vector of each algorithm sums to the respective performance
values from Table 4. This allows the better performing algorithms to have a larger vote in the final model
which is logical since they perform better and should be trusted more.
We tested the equal weight and performance weighted voting scheme for a hybrid model combining all
algorithms. We also created three more hybrid models all using performance vote. These three other hybrid
models and the algorithms they contain are shown in Table 5.
Table 5: Hybrid Models tested and the individual algorithms used in their respective voting schemes.
Hybrid Model Algorithms
Weaker Models
Naive Bayes
Logistic Regression
Decision Tree
Stronger Models
k-NN
Full Gaussian
SVM
Neural Network
Fastest Models
Naive Bayes
k-NN
Decision Tree
An example of the votes from each algorithm and the resulting total vote for the equal vote scheme and
for a test letter G is shown in Table 6. In this vote, six of the seven algorithms correctly predict the letter
and the resulting final vote’s maximum value also predicts the correct letter. One will notice that each
algorithm’s vote vector has a slightly different structure. The Naive Bayes, GMM, Logistic Regression, and
Neural Network algorithms are able to vote for multiple letters while the k-NN, Decision Tree, and SVM vote
for only a single letter. This is simply due to the nature of each of the algorithms. The algorithms that vote
for multiple letters have a posteriori predictions or comparable scores for each letter while the algorithms
that vote for only a single letter do so because the algorithm is a discriminative classifier with only a single
output. The Multiclass SVM outputs a score for every letter, but those scores are not representative of the
probability that the test letter belongs to each class, so the SVM therefore submits its full vote to only the
single letter with the maximum value from the algorithm.
One should also note that the Neural Network’s vote vector contains negative values and that the vote for
the correct letter G is also greater than one. This is due to the fact that the neural network is constructed to
minimize the mean-square error, and that we are using a regression based algorithm as a classifier. Therefore
if one were trying to train a neural network on an output of 0, a result of -0.01 would be equivalent to a
resulting output of 0.01 from a mean-square error perspective. This is a possible source of corruption in the
voting scheme.
The final performance results for the hybrid algorithms are shown in Table 7. There is only a very
small improvement over the neural network for the equal, performance, and strong model voting schemes.
Similarly there is only a small improvement over the decision tree for the weak models. The results for the
fast models are in fact worse than the k-NN results on their own.
This lack of improvement is due to a number of factors. When algorithms are combined that only vote
for a single letter, there isn’t a lot of room to improve when combining only three or four algorithms. Also
for some of the stronger performing models, there isn’t a lot of room to improve on the performance anyway.
However the lack of improvement is also due to the nature of the data. Table 8 shows the amount of overlap
15

16. Table 6: Resulting votes for example test letter G.
LR DT NN SVM NB GMM KNN SUM
A 0.000 0 0.001 0 0.000 0.000 0 0.001
B 0.000 0 -0.024 0 0.000 0.000 0 -0.024
C 0.484 0 -0.222 0 0.011 0.009 0 0.282
D 0.000 0 -0.005 0 0.000 0.000 0 -0.005
E 0.028 0 -0.054 0 0.000 0.000 0 -0.026
F 0.000 0 -0.022 0 0.000 0.000 0 -0.022
G 0.287 1 1.273 1 0.981 0.991 1 6.532
H 0.033 0 -0.055 0 0.000 0.000 0 -0.022
I 0.000 0 0.005 0 0.000 0.000 0 0.005
J 0.000 0 0.003 0 0.000 0.000 0 0.003
K 0.011 0 0.018 0 0.000 0.000 0 0.029
L 0.048 0 -0.006 0 0.000 0.000 0 0.042
M 0.000 0 0.000 0 0.000 0.000 0 0.000
N 0.012 0 0.004 0 0.000 0.000 0 0.016
O 0.069 0 -0.001 0 0.007 0.000 0 0.075
P 0.000 0 -0.001 0 0.000 0.000 0 -0.001
Q 0.010 0 0.007 0 0.000 0.000 0 0.017
R 0.000 0 -0.017 0 0.000 0.000 0 -0.017
S 0.009 0 -0.005 0 0.000 0.000 0 0.004
T 0.000 0 0.010 0 0.000 0.000 0 0.010
U 0.007 0 0.032 0 0.000 0.000 0 0.039
V 0.000 0 0.008 0 0.000 0.000 0 0.008
W 0.000 0 0.003 0 0.000 0.000 0 0.003
X 0.001 0 0.005 0 0.000 0.000 0 0.006
Y 0.000 0 0.000 0 0.000 0.000 0 0.000
Z 0.000 0 0.043 0 0.000 0.000 0 0.043
Table 7: Test performance results for the hybrid models.
Algorithm Performance Time to Run (s)
Equal Weight 97.22% 2374
Performance Weight 97.50% 2374
Weak Models 85.38% 3.2
Strong Models 97.48% 2371
Fast Models 94.93% 1.3
16

17. Table 8: Amount of shared overlap of misclassifications among the algorithms in the Weak and Strong hybrid
models.
Weak Models Strong Models
Algorithm # Misclassifications Overlap Algorithm # Misclassifications Overlap >3
Naive Bayes 1502
306
k-NN 174
77
Logistic Regression 1139 Full Gaussian 149
Decision Tree 586 SVM 164
Neural Network 119
in misclassifications among the individual algorithms in both the weak and strong hybrid models. Compared
to the best performing model in each situation, there is a large amount of overlap in the misclassifications
between the models. This leaves very few test cases where fixed classifications could be expected. Generally
hybrid models such as these tend to work best with a larger amount of weaker models, since there are more
possible votes and more room for improvement.
3.10 Final Confusion Matrix
We present the confusion matrix for the best performing performance-weighted vote in Figure 13. Highlighted
in green are the correct predictions for each letter and highlighted in red are some of the interesting and
most frequent letter misclassifications. We perform worst on the letter H, correctly predicting it only 93%
of the time. Some misclassifications include mistaking the letter I for J and vice-versa. It should be noted
that the confusion matrix is not symmetric, meaning that even though one letter is often misclassified as a
second it does not mean that the second letter gets misclassified as the first, although that is not an unusual
scenario. This is because some of the letters can be better discriminated than others, and some are closer
to the general distribution of the remaining letters than others. For example the letter K is misclassified as
an R 3% of the time, while the letter R is misclassified as the letter K only 1% of the time.
In general this confusion matrix matches up well with our general intuition of how the classifications would
perform. Letters that are most frequently misclassified as others tend to have a significant resemblance to
the human eye.
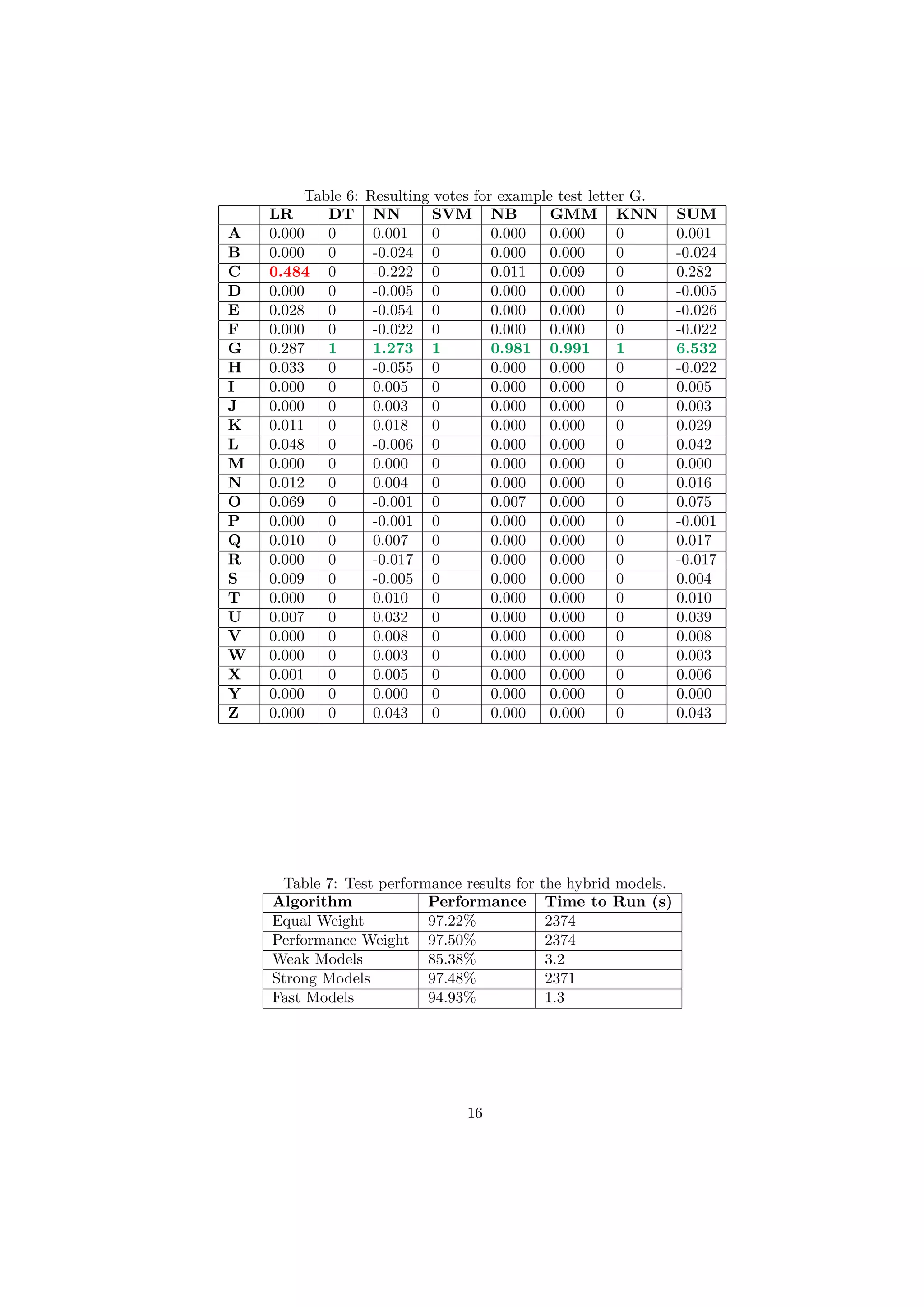
4 Conclusions
We used seven different machine learning algorithms to classify letter images based on 16 predetermined
features. Our best performance was accomplished with a neural network at 97.18%. We were able to slightly
increase this result to 97.50%. using a voting scheme among many models. However the improvement with
the hybrid models was less than originally hoped for due to the already good performance from the original
models, as well as the nature of the data, in that the letters that were misclassified were often commonly
misclassified by most of the individual algorithms.
References
[1] P. W. Frey and D. J. Slate, “Letter recognition using holland-style adaptive classifiers,” Mach. Learn.,
vol. 6, pp. 161–182, Mar. 1991.
[2] C. M. Bishop, Pattern Recognition and Machine Learning (Information Science and Statistics). Secaucus,
NJ, USA: Springer-Verlag New York, Inc., 2006.
[3] Z.-B. Joseph, “10701 machine learning, neural network lecture slides,” 2012.
17

18. Figure 13: Confusion matrix for test data. Rows represent the actual test letter, with each clumn in the
row representing the fractional amount that column’s letter class was predicted as the class for the row test
letter.
18